À la surface des choses/L’énergie/Enchaînements entre changements efficients

Jean Perrin

À la surface des choses : L’énergie

Hermann, 1941 (6, p. 21-38).

ENCHAÎNEMENTS
ENTRE CHANGEMENTS EFFICIENTS

Nous voulons maintenant, généralisant ce que nous savons quant aux travaux moteurs et résistants, expliquer et comparer les enchaînements par lesquels peuvent se conjuguer, sans autre répercussion, des changements efficients.

16. Enchaînement d’un travail moteur avec un travail résistant. — Malgré que nous l’ayons déjà fait avec détail (IV, 11 à 15), nous voulons d’abord, dans cet esprit, rappeler le long effort par lequel les hommes ont fini par se convaincre qu’un poids ne peut s’élever « tout seul », ou, comme on a dit plus improprement, que le « mouvement perpétuel » est impossible.

Ayant compris que, par exemple, au moyen de poulies ou de treuils, nous pouvons acheter l’élévation du poids $\mathrm {P} '$ de la hauteur $h'$ par l’abaissement d’un poids $\mathrm {P}$ de la hauteur $h$, sans autre répercussion, sous la condition que les produits $\mathrm {P} h$ et $\mathrm {P} 'h'$ soient égaux (les deux changements se décomposant donc l’un et l’autre en autant de kilogrammètres), nous nous sommes demandé si quelque autre mécanisme, quelque autre genre d’enchaînement, permettrait de faire un marché plus avantageux, élevant par exemple en surplus un poids $\mathrm {P} ''$ de la hauteur $h''$. En ce cas, nous pourrions toujours, par treuils ou poulies, remonter sans autre répercussion le poids $\mathrm {P}$ de la hauteur $h$, en abaissant de la hauteur $h'$ le poids $\mathrm {P} '$ d’abord élevé, en sorte qu’il resterait, que le poids $\mathrm {P} ''$ se serait élevé tout seul sans répercussion. Avec Galilée, nous avons jugé cela impossible et ainsi nous avons compris que :

Il y a équivalence entre tous les enchaînements qui achètent du travail résistant avec du travail moteur.

Nous allons élargir et généraliser ce principe, par étapes successives.

Et d’abord, discutons les enchaînements par lesquels l’arrêt ou le lancement d’un mobile se trouvent conjugués, soit avec un travail, soit avec le lancement ou l’arrêt d’un autre mobile.

17. Dévier un mobile exige un effort, mais ne coûte pas de travail. — Soit un point matériel en mouvement par rapport au sol.

Cherchons à changer sa vitesse. Des forces vont être nécessaires ; mais l’opération n’est pas de même sorte selon que nous voulons changer la direction de la vitesse ou changer sa grandeur. Dévier un projectile ou l’arrêter sont choses bien différentes.

Considérons d’abord un point matériel en mouvement rectiligne et uniforme sur un plan horizontal fixé au sol et qui le soutient. Un moyen de changer la direction de cette vitesse, de « dévier » la course du mobile est de le saisir dans une position $\mathrm {M}$ par un fil $\mathrm {O} \mathrm {M}$ de longueur $\mathrm {R}$ attaché à un point ou pivot $\mathrm {O}$ fixé sur le plan, fil à ce moment rectiligne et perpendiculaire à la vitesse en $\mathrm {M}$ et qu’enfin nous supposons pratiquement inextensible (fig. 2).

Sitôt le mobile saisi par ce fil, il ne peut continuer son mouvement rectiligne et décrit forcément, par rapport au sol, un cercle ayant $\mathrm {O}$ pour centre, en même temps que le fil se tend, tirant ce mobile vers ce point $\mathrm {O}$, avec une force $\mathrm {F}$, normale au mouvement, qui laisse donc constante la vitesse $v$. Mais, dès que nous supprimerons cette force^[1] disons au point $\mathrm {M} '$, le mouvement redeviendra rectiligne, tangent en $\mathrm {M} '$ au cercle abandonné ; la direction de la vitesse aura été déviée de l’angle $\mathrm {M} \mathrm {O} \mathrm {M} '$.

Cette déviation a été produite sans que le fil tendu ait travaillé (le produit de la force par la variation nulle de la longueur du fil étant nul). La déviation du mobile a exigé qu’une force s’exerçât pendant un certain temps, qu’il y eût « effort » mais non pas travail, car elle n’a rien dépensé qui eût pu servir à élever un poids. Et nous pourrions indéfiniment recommencer l’opération ; nous ne sommes à cet égard ni appauvris, ni enrichis : la déviation est gratuite, en ce qui regarde la réserve dont nous pouvons disposer pour élever des poids.

J’observe qu’il est intéressant de définir un effort scalaire (relatif à la corde qui tire le mobile) aussi bien que l’effort vectoriel antérieurement défini (V, 16). Cet effort scalaire est la somme des grandeurs $\mathrm {F} dt$ des efforts vectoriels élémentaires successifs.

Il est égal, ici, au produit de l’impulsion par la déviation. Soit $\alpha$ cette élévation.

La force $\mathrm {F}$ qui tire le mobile de masse $m$ vers le centre $\mathrm {O}$ est $m{\tfrac {v^{2}}{\mathrm {R} }}$ (voir V, 8). D’autre part, l’arc $\alpha$ décrit $\mathrm {R}$ avec la vitesse $v$ constante est égal à $vt$. En sorte que :

$\mathrm {F} =m{\frac {v^{2}}{\mathrm {R} }}={\frac {mv^{2}\alpha }{vt}}\qquad {\text{ou}}\qquad \mathrm {F} t=\alpha mv.$

Nous avons supposé la vitesse horizontale. Cette restriction peut être levée. Soit un point matériel qui va passer en $\mathrm {M}$ dans la direction $\mathrm {Mx}$, avec une certaine vitesse (fig. 2). Sur $\mathrm {Mx}$, au delà de $\mathrm {M}$, menons par un point $\mathrm {A}$ très voisin un axe $\mathrm {Ay}$ arbitraire, le long duquel nous voulons dévier le mobile. Pour cela, réalisons un axe lié au sol, et perpendiculaire au plan $\mathrm {Axy}$, tel que sa trace $\mathrm {O}$ sur le plan $\mathrm {Axy}$ soit centre du cercle tangent à $\mathrm {Ax}$ en $\mathrm {M}$, et à $\mathrm {Ay}$ en un point $\mathrm {M^{\prime }}$. Soient $\mathrm {O}$ et $\mathrm {O^{\prime \prime }}$ deux points fixes de cet axe, et supposons le mobile saisi, quand il passe en $\mathrm {M}$, par les deux cordons inextensibles $\mathrm {O^{\prime }M}$ et $\mathrm {O^{\prime \prime }M}$ à ce moment rectilignes. Le mobile est alors forcé de décrire le cercle de rayon $\mathrm {OM}$ ; coupons les fils en $\mathrm {M^{\prime }}$, nous avons obtenu la déviation.

Nous l’avons obtenue « pour rien », car sur l’espace très petit $\mathrm {MM^{\prime }}$ les forces qui agissent sur le mobile n’ont pu effectuer de travail notable, et, d’autre part, si puissant qu’ait été « l’effort », nos cordons n’ont pas travaillé.

Il est d’ailleurs évident que la relation qu’on vient d’établir entre l’effort scalaire, la déviation, et l’impulsion, subsiste.

Bref, cela ne peut ni coûter ni rapporter de travail, de changer la direction d’un mobile en mouvement, de dévier un projectile. C’est un changement indifférent gratuit. Il n’en va pas de même s’il s’agit de ralentir ou d’accélérer le projectile.

18. Tout lancement de mobile coûte, et tout arrêt enrichit. — Comme pour ce qui regarde la production de travail, des observations familières en nombre immense ont imposé la conviction que, par rapport au sol, la mise en mouvement d’un mobile ou l’accroissement de sa vitesse ne se font jamais « tout seuls ». Il n’arrive jamais qu’un projectile soit lancé sans qu’il se soit produit par ailleurs quelque phénomène « moteur » (tel qu’un abaissement de poids, ou un ralentissement de quelque autre mobile, ou la détente d’un ressort, ou la combustion de la poudre d’une cartouche) qui, de façon évidente, selon tel ou tel enchaînement, a déterminé le lancement. Et, encore comme pour le travail, ce sera là une vraie dépense, proportionnelle au résultat, avec un changement extérieur qui nous laisse appauvris puisque nous aurons par exemple, ensuite, moins de poudre disponible, et que notre capital en possibilités de lancement sera diminué.

Symétriquement, il n’arrive jamais que, par rapport au sol, la vitesse d’un mobile diminue sans qu’il se passe quelque part une répercussion, d’autant plus importante que le mobile est plus massif et plus rapide. Un projectile déterminera par exemple, en s’arrêtant, des travaux résistants ou des échauffements.

Nous sommes, en particulier, assurés qu’une déviation de projectile dont nous venons de voir qu’on l’obtient gratuitement, laisse la vitesse inchangée.

19. Enchaînement de lancement ou d’arrêt avec travail. — Un travail moteur, qui peut « acheter » (12) un travail résistant, peut aussi bien acheter un lancement de mobile. De même, l’arrêt du mobile peut acheter un travail résistant ou lancer un autre mobile. Travail moteur et arrêt de mobile sont deux phénomènes moteurs ; travail résistant ou lancement de mobile sont deux phénomènes résistants.

Le treuil permet de réaliser ces quatre genres d’enchaînements.

Nous savons déjà comment il permet de conjuguer (12) un travail moteur avec un travail résistant (enchaînement $a$).

Nous pouvons maintenant imaginer (fig. 3) qu’un poids $\mathrm {P}$, suspendu par un fil enroulé sur la gorge de la petite poulie, entraîne horizontalement le chariot ou traîneau $\mathrm {A}$, par l’intermédiaire d’un fil passé sur la grande poulie, lançant ainsi progressivement ce chariot avec une vitesse qui sera devenue $v$ quand le poids $\mathrm {P}$ sera descendu de $h$ (enchaînement $b$). Le rapport des rayons des poulies aura été pris assez grand pour que, même à ce moment, le mouvement de descente du poids $\mathrm {P}$ soit très lent, et que ce poids soit presque en équilibre, le travail qu’il a fourni étant $\mathrm {P} h$.

Réciproquement, le chariot lancé en sens inverse remonterait le poids, le laissant à chaque instant presque en équilibre (enchaînement c).

Enfin, le chariot ayant, en s’arrêtant, remonté de $h$ le poids $\mathrm {P}$, nous pouvons décrocher ce chariot, le laissant en repos, puis accrocher un autre chariot sur une autre poulie du treuil (généralisé) ; $\mathrm {P}$ redescendra de $h$ et sera dans son état initial, et il reste en définitive à ce moment un deuxième chariot lancé par suite de l’arrêt d’un premier (enchaînement $d$). Cet enchaînement $d$, formé d’abord d’un enchaînement $c$ [travail produit par l’arrêt du premier mobile, puis d’un enchaînement $b$ (lancement du second mobile par dépense de ce travail)] n’est ici pas direct. Mais on peut réaliser des enchaînements directs d’espèce $d$.

Étendant la notion de treuil, imaginons en effet au lieu de deux poulies circulaires solidarisées sur un même axe, deux poulies coniques solidarisées sur cet axe, chacune à gorge spiralée courant de la base au sommet du cône formant la poulie conique. Le système qu’on veut ralentir sollicite par un fil $\mathrm {F}$ ce treuil spiralé, tirant sur l’un des cônes près de la base où le rayon est grand ;

celui qu’on veut lancer est tiré par un fil $\mathrm {F'}$ tirant en sens inverse sur la gorge de l’autre cône, dans la région, proche du sommet, où les spires sont petites ; il peut ainsi partir avec une vitesse faible, qui grandira progressivement à mesure que son fil d’attache se rapprochera de la base du cône ; au contraire, le chariot moteur, dont le fil s’approche du sommet du cône, pourra, même si sa vitesse tend vers zéro, accroître encore la vitesse, devenue grande, du second chariot. Il est manifeste qu’on pourra s’arranger, avec gorges spirales convenables, pour que la traction due au chariot qui se ralentit garde, par rapport à l’axe, un moment toujours un peu supérieur à la traction exercée par le chariot qui s’accélère (fig. 4).

Ainsi divers mécanismes peuvent réaliser les quatre genres d’enchaînements entre les phénomènes moteurs « travail moteur » et « arrêt de mobile » et les phénomènes résistant « travail résistant » et « lancement de mobile ». Le schéma ci-contre (fig. 5), qui sera généralisé, indique, par le moyen de flèches allant du phénomène « cause » au phénomène « effet », le sens et la possibilité de ces enchaînements. Nous allons montrer que les mécanismes qui peuvent les produire sont tous équivalents.

Nous allons, pour cela, suivant l’ordre historique du développement des idées, faire intervenir des abaissements ou élévations de poids en « chute libre » ou « ascension libre », mais nous devons d’abord expliciter une propriété remarquable de la pesanteur, au fond déjà admise dans les énoncés qui précèdent.

20. Le poids d’un corps ne dépend pas de sa vitesse. — Considérons la force que développe le vent sur un bateau qu’il pousse par l’arrière. Le travail de cette force entre deux positions de ce bateau, et la force elle-même, ne sont pas les mêmes si le bateau avance très lentement (la poussée exercée par le vent restant alors constante) ou s’il avance de plus en plus rapidement (la poussée exercée par le vent diminuant alors, jusqu’à s’annuler si la vitesse du bateau devient égale à celle du vent). De même il se pourrait que le poids d’un corps diminuât, quand ce corps tombe dans la direction de la pesanteur, ce poids étant une fonction décroissante $\varpi (v)$ de la vitesse verticale. Alors que le travail de la pesanteur sur un corps, ayant en équilibre le poids $\mathrm {P}$, et qui descend très lentement de la hauteur $h_{0}$ est $\mathrm {P} _{0}h_{0}$, il serait inférieur, et de la forme $\textstyle \int _{0}^{h}\varpi (v)dh$ quand le corps tombe en chute libre.

C’est ce qui n’a pas lieu ; laissons tomber le corps en chute libre de cette hauteur $h_{0}$ et prendre ainsi une vitesse $v$. Dévions-le alors sans changer son niveau (ceci ne coûte rien), en sorte qu’il coure avec cette vitesse sur un plan horizontal, et accrochons-le alors à un fil tendu sur la poulie extérieure d’un treuil (fig. 5) dont un poids $\mathrm {P}$ sollicite en sens inverse la poulie intérieure, en sorte que l’ascension de $\mathrm {P}$ soit aussi lente qu’on le veut, même quand le mobile a sa plus grande vitesse. Bientôt ce mobile s’arrêtera, ayant remonté de $h$ un poids $\mathrm {P}$ qui est pratiquement resté toujours en équilibre. Fixons à cet instant ce mobile par une clavette. Aucun changement ne se trouve alors réalisé, hors que $\mathrm {P} _{0}$, de nouveau en équilibre, est descendu de $h_{0}$ et que $\mathrm {P}$, aussi en équilibre, a remonté de $h$.

Si le travail $\textstyle \int \varpi dh$ fourni pendant la chute, et qui, selon le principe de Galilée, doit se retrouver dans l’élévation de $\mathrm {P} ,$ était inférieur à $\mathrm {P} _{0}h_{0}$, le travail égal $\mathrm {P} h$ serait aussi inférieur à $\mathrm {P} _{0}h_{0}.$ Et, remontant par une machine simple fonctionnant sans vitesse ce que nous pourrions du poids $\mathrm {P} _{0}$ à son niveau primitif, il nous resterait qu’une certaine partie de ce poids se trouverait abaissée, sans effet extérieur produit. En regardant cela comme impossible, nous avons donc implicitement admis que le poids d’un corps en mouvement est égal au poids du corps en repos.

Un raisonnement analogue s’appliquerait aux forces électriques ; elles ne dépendent pas de la vitesse du corps chargé.

21. Équivalence des enchaînements entre lancements ou arrêts et travaux. — Maintenant nous pouvons établir l’équivalence des mécanismes qui enchaînent travaux et variations de vitesse.

Une façon de lancer un objet par abaissement d’un poids (flèche $b$) est simplement de laisser tomber cet objet en « chute libre ». La pesanteur agit alors seule, et, pour la hauteur de chute $h$, qui donne au mobile une vitesse $v$, dépense un travail $\mathrm {P} h$. Au prix de ce travail, nous ne pourrons faire ni mieux, ni plus mal.

Nous savons, en effet (treuil de la figure 3), que nous pourrons alors, en arrêtant le corps lancé, soulever un poids égal $\mathrm {P}$ d’une hauteur $h$, retrouvant le travail $\mathrm {P} h$, dépensé pendant la descente. Si, par un autre mécanisme que la chute libre, nous avions obtenu une vitesse supérieure pour la même dépense initiale $\mathrm {P} h$, nous pourrions, déviant le corps lancé sur un plan horizontal et l’attachant à la poulie extérieure de notre treuil, lui faire remonter plus haut le poids égal $\mathrm {P}$ soulevé par le treuil et avoir en définitive « pour rien » une élévation de poids. Et si notre mécanisme était moins avantageux que la chute libre, c’est un abaissement « perdu », sans effet, qui nous resterait comme seul changement.

Considérons maintenant l’enchaînement $c$ où l’arrêt d’un mobile effectue un travail résistant, par exemple élève un poids. Ce mobile eût pu prendre sa vitesse $v$ en chute libre de hauteur $h$, sous l’action de son poids $\mathrm {P}$. Cela dit, si (après qu’on l’a dévié, de façon que son mouvement, renversé, se dirige vers le haut) il perd sa vitesse par ascension libre (transformation $c$), il est forcément monté de $h$, sans quoi nous aurions, à partir de son état de repos, un poids monté tout seul ou descendu sans effet. Et il n’arrivera pas qu’un mécanisme autre que l’ascension libre, en arrêtant le mobile lancé à la vitesse $v$, élève $(\mathrm {P} +p)$ de la hauteur $h$ ; sans quoi, laissant retomber $\mathrm {P}$ de $h$, nous retrouverions le mobile lancé à la vitesse $v$ avec un travail $ph$ obtenu pour rien. (Démonstration analogue, si notre mécanisme était supposé moins avantageux que l’enchaînement par ascension libre).

Enfin, nous savons lancer un second mobile par arrêt d’un premier (enchaînement $d$). Supposons cela fait par deux mécanismes différents. Arrêtons le second mobile en lui faisant remonter un poids. Tout se réduit alors à ce que le premier mobile est arrêté et le poids remonté (enchaînement $c$) ; cette élévation de poids a donc une valeur fixée ; tandis qu’elle prendrait deux valeurs différentes si nos mécanismes n’étaient pas également avantageux.

Bref, le principe d’équivalence de Galilée se trouve étendu aux lancements ou arrêts de mobiles.

Nous allons en obtenir des généralisations d’autres sortes.

22. Changements thermiques. — Nous avons acquis la notion de température en partant de ce que deux corps peuvent se modifier réciproquement par conductibilité ou rayonnement.

Nous appellerons « changements thermiques » les changements qui peuvent être ainsi produits en conséquence de différences de température, sans intervention d’aucune autre action, et avec retour possible à l’état initial si la température primitive est restaurée (ceci excluant les actions photochimiques, ou les travaux produits par pression de radiation). Tel le changement efficient « congélation d’eau » que peut payer, par mise en contact, le changement « fusion de mercure solide ». Tel le changement « fusion de glace » qui peut être produit en mettant la glace sur un fourneau (conductibilité) ou en l’exposant devant un feu ardent (rayonnement). Tel encore le changement de 1 gramme d’eau pris à la température de 15° et laissé à celle de 16°. Ce dernier changement, qu’on utilise commodément en des enchaînements de changements thermiques, définit la calorie.

On ne manquera pas de remarquer que les changements thermiques produits dans un objet froid par action d’un objet chaud peuvent être achetés, au moyen de frottements, par du travail moteur ; mais, même alors, le changement se produit en conséquence d’élévations de température (faibles et transitoires, mais inévitables) dues au frottement. Et le changement considéré se produit en définitive toujours par voie thermique.

Les changements thermiques peuvent être conjugués avec une apparition ou une disparition de Lumière (45) : par exemple, de la lumière jaune absorbée par un système qu’elle échauffe peut toujours être regardée comme provenant, au travers d’un écran sélecteur qui n’en laisserait pas sortir d’autre, d’un objet à température suffisamment élevée, qui par là se refroidit.

Comme pour l’élévation ou l’abaissement d’un poids, comme pour le lancement ou l’arrêt d’un mobile, des observations familières en nombre immense ont imposé la conviction que les changements thermiques ne peuvent se produire « seuls », ne peuvent constituer des changements isolés. Et, comme pour les travaux, ou comme pour les mobiles dont la vitesse change, nous pouvons distinguer des changements thermiques « moteurs » et des changements thermiques « résistants ».

Sont « résistants » ou « positifs » à la façon d’un lancement de projectile, ou d’une élévation de poids et plus généralement d’un travail résistant, les changements thermiques produits au prix d’un phénomène « moteur » (tel que l’abaissement d’un poids, ou la détente d’un ressort, ou l’arrêt d’un projectile). Ces changements thermiques « résistants » ou « positifs », (échauffements, fusions, émissions de lumière, etc.) peuvent toujours être produits par action thermique d’un corps « chaud », qui alors se refroidit.

Symétriquement sont « moteurs » ou « négatifs » les changements thermiques (refroidissements, congélations, absorptions de radiation, etc.) qui enrichissent l’extérieur comme peut faire un abaissement de poids, étant capables, par exemple, de déterminer l’échauffement d’un corps « froid ».

23. Équivalence des enchaînements entre changements thermiques. — Un changement thermique a été défini comme pouvant être la cause ou l’effet d’un autre changement thermique, rien d’autre ne se passant. Par exemple la fusion de glace peut être achetée par le refroidissement d’une masse de mercure qui passe de la température de l’eau bouillante à celle de la glace fondante, sans autre répercussion.

Faisant cette expérience, en versant directement le mercure chaud dans la glace fondante, nous trouverons, par kilogramme de mercure, 42 grammes de glace fondue. Pouvons-nous, au prix du même refroidissement, mais en nous y prenant autrement, réussir un « marché » plus avantageux, par exemple fondre 50 grammes de glace ?

Nous ne pouvons plus répéter ici le raisonnement par lequel nous avions répondu à une question semblable (IV, 14) au sujet de l’élévation d’un poids par l’abaissement d’un autre poids. Nous ne pouvons plus dire que nous n’avons qu’à renverser le premier enchaînement pour réchauffer notre kilogramme de mercure en recongelant 42 grammes de glace, après quoi il nous resterait 8 grammes de glace fondue « gratuitement », ce que nous regardons comme impossible. Nous ne pouvons plus le dire parce que nous ne savons pas renverser l’enchaînement « fusion de glace par refroidissement d’un corps plus chaud » (et bientôt nous reconnaîtrons qu’il y a là une impossibilité essentielle).

Nous affirmerons cependant, après bien des essais, qu’il n’est pas possible, en un changement isolé qui se réduise au refroidissement de un kilogramme de mercure et à de la fusion de glace, de trouver jamais plus (ni moins) que 42 grammes de glace fondue. Plus généralement, l’expérience a toujours donné une équivalence exacte entre les divers procédés par lesquels on sait enchaîner deux changements thermiques.

24. Calorimètre. — C’est la validité générale de cette équivalence qui a rendu possible la « calorimétrie », c’est-à-dire la mesure des changements thermiques (ou, comme on dit souvent pour des raisons que nous donnerons, la mesure des « quantités de chaleur »), dans les opérations où interviennent seulement des actions thermiques.

Un changement thermique « résistant », « positif », aura pour mesure le nombre $(+n)$ s’il « vaut » $n$ fois un certain changement thermique positif choisi comme unité (on choisit généralement la calorie), c’est-à-dire s’il peut être payé par un changement thermique qui pourrait aussi bien payer le changement thermique constitué par $n$ fois le changement unité (soit $n$ calories).

On voit que la somme des valeurs de deux changements thermiques payés l’un par l’autre est nulle.

La notion de changement thermique, fixée avec l’état initial et l’état final, ou, si on préfère, celle de quantité de chaleur perdue ou gagnée entre ces deux états, n’a été clairement dégagée qu’au XVIII^e siècle, notamment grâce au physicien anglais Black.

La mesure se fait au moyen d’un calorimètre, système matériel assujetti, comme un thermomètre ou un thermostat, à ne connaître l’extérieur que par action thermique. Ce sera, par exemple, un calorimètre à eau (fig. 6) constitué par une masse connue d’eau contenue dans un vase métallique mince soutenu par des supports isolants au sein d’une enceinte métallique protectrice à double paroi, emplie d’eau sensiblement à la même température.

Soit à déterminer, au voisinage de la température ordinaire, la chaleur spécifique du métal dont est fait le vase calorimétrique (disons, du cuivre). C’est-à-dire soit à trouver la valeur $c$ du changement thermique subi par 1 gramme de ce métal quand sa température varie de 1° au voisinage de 15°. Soit $\mathrm {M}$ la température initiale. Nous trouverons que $m$ grammes de ce métal à la température $\mathrm {T}$, immergés dans le calorimètre, l’amènent à la température $\theta$, une fois l’équilibre établi. Le changement thermique de la masse $\mu$ immergée est alors $-mc(\mathrm {T} -\theta )$, celui de l’eau est $\mathrm {M} (\theta -t)$ et celui du vase est $\mu {c}(\theta -t)$. Donc, écrivant que la somme des deux changements thermiques payés l’un par l’autre est nulle, on a :

$\mathrm {M} (\theta -t)+\mu {c}(\theta -t)-mc(\mathrm {T} -\theta )=0$

ce qui donnera $c$, soit 0,1 calorie dans le cas du cuivre.

Il est essentiel de comprendre que nous trouverons toujours même valeur pour $c$, de quelque façon que soit conduite l’expérience.

Après quoi, désignant par $\mathrm {A}$ la somme $(\mathrm {M} +{\mu }c)$ désormais connue, appelée souvent « valeur en eau du calorimètre », nous aurons toute autre chaleur spécifique $c'$ par une équation de même sorte :

$A(\theta _{1}-t_{1})=m'c'(\mathrm {T_{1}} -\theta _{1}).$

Nous mesurerons de même, par exemple, le changement thermique « fusion de 1 gramme de glace à la température 0° de la glace fondante » ou « chaleur latente de fusion de la glace », de valeur $\varphi$, selon une équation :

$\mathrm {A} (t-\theta )={\mu }\varphi +{\mu }\theta$

trouvant ainsi pour $\varphi$, quelle qu’ait été la façon de procéder, 80 calories.

Et ainsi de suite.

Il va de soi que nous pourrons changer le liquide calorimétrique et le vase qui le contient. (Nous aurons notamment avantage à prendre pour vase calorimétrique un vase d’Arsonval-Dewar). Nous déterminerons la « valeur en eau » $\mathrm {A}$ du nouveau calorimètre, par exemple en y versant une masse $m$ d’eau à une température $\mathrm {T}$ et mesurant la température $\theta$ une fois l’équilibre réalisé, d’où l’équation :

$\mathrm {A} (\theta -t)=m(\mathrm {T} -\theta )$

Nous pourrons substituer au calorimètre à eau un calorimètre à glace fondante, (mesurant le poids de glace fondue quand on y introduit l’objet dont on mesure le changement thermique) ou employer tout autre genre de calorimètre. Dans tous les cas, quels que soient les intermédiaires entre l’état initial et l’état final, la mesure d’un même changement thermique, disons la fusion de 1 gramme de glace à 0°, donne le même résultat.

Au XVIII^e siècle, on interprétait cette concordance en admettant l’existence d’un fluide calorifique indestructible ou « chaleur » qui abandonnait le corps refroidi pour entrer dans le corps échauffé. L’équation calorimétrique exprimait que la chaleur perdue par un corps était gagnée par l’autre, en sorte qu’il y eût « conservation du calorique ». Ce postulat fut abandonné quand on s’avisa que le frottement peut « créer » du calorique, mais il reste que la cohérence des résultats de la calorimétrie établit pour les changements thermiques un principe d’équivalence analogue à celui que nous avons énoncé pour les changements mécaniques, c’est-à-dire que :

Aucun dispositif n’est plus avantageux qu’un autre pour « acheter » un changement thermique d’une sorte donnée (disons fusion de glace) avec un changement thermique d’une autre sorte donnée (disons refroidissement de cuivre).

Nous comprendrons au surplus bientôt, quand nous aurons dégagé la notion d’énergie, qu’il n’était aucunement incorrect de parler de quantité de chaleur ou de déplacement de chaleur, à la condition de ne pas considérer cette chaleur comme indestructible en tant que chaleur.

24. Thermochimie. — Considérons une réaction chimique accomplie sans travail, dont la répercussion extérieure se réduit à un changement thermique. Par exemple considérons le système matériel constitué par : 1,7 gr. de gaz ammoniac, 3,65 gr. de gaz chlorhydrique, et 100 grammes d’eau liquide, chacune de ces matières étant prise à 0° sous la pression atmosphérique (état initial). Nous pouvons de bien des manières transformer ce système en une solution aqueuse de sel ammoniac à 0° sous la pression atmosphérique (état final), par exemple en laissant les deux gaz se mélanger puis le sel ammoniac se dissoudre, ou en laissant dissoudre le gaz chlorhydrique dans la moitié de notre eau, le gaz ammoniac dans l’autre moitié et en mélangeant les deux solutions.

Si cependant on a veillé, comme il est ici facile, à ce que toute répercussion extérieure se réduise à des changements thermiques, en définitive toujours réductibles à la production de calories, nous trouverons que par tous les moyens employés, nous obtenons le même nombre de calories. Ici encore il n’est pas possible, au prix d’un même changement chimique et sans autre répercussion extérieure, d’obtenir par un moyen la fusion de dix grammes de glace et par un autre moyen plus avantageux la fusion, disons, de douze grammes de glace. De nouveau nous voyons que la Nature vend à prix fixe. Dans le langage utilisant l’hypothèse du calorique, on disait que la « quantité de chaleur » dégagée dans une réaction, où l’état initial et l’état final sont donnés, est déterminée. C’est ce qui a été clairement compris, et énoncé comme « principe de l’état initial et de l’état final », au xix siècle par le chimiste français Berthelot, et depuis appliqué dans les innombrables mesures thermochimiques exécutées par Berthelot en France, Thomsen en Allemagne, et par leurs continuateurs.

Considérons des réactions dont l’état initial et l’état final sont tels que la répercussion puisse en être entièrement thermique, comme il arrive pour les réactions produites dans un récipient rigide (« bombe calorimétrique » de Berthelot), qui sera plongé dans un calorimètre. Ces réactions seront dites exothermiques si le changement thermique extérieur correspondant est positif, endothermiques s’il est négatif.

26. Enchaînement, par frottement, d’un travail avec un changement thermique. — Les frottements vont enfin nous permettre de lier changements thermiques et mécaniques et d’atteindre en sa forme générale la notion d’équivalence des changements.

Nous avons indiqué déjà comment l’observation journalière donne l’exemple de travaux produisant des échauffements par frottement. Rumford, dès le xviii^e siècle, comme nous l’avons alors rappelé (1), avait ainsi amené à l’ébullition l’eau d’une grande cuve, par frottement, au sein de cette cuve, contre une pièce métallique immobile, d’une autre pièce maintenue en rotation par un manège que faisaient tourner des chevaux. Et cette expérience où se créait du « calorique », sans qu’aucune matière fût transformée, par suite sans qu’aucune matière eût pu en perdre, fut justement opposée à l’hypothèse de la conservation du calorique.

Il y avait dès lors peu à faire pour introduire la mesure en de telles expériences. Peu à faire sinon précisément de comprendre l’intérêt immense de cette mesure. Il fallut attendre pour cela Joule (1845), dont l’expérience fondamentale (qui au fond n’est qu’une modification de l’expérience de Rumford) peut être résumée comme il suit :

Deux poids, en s’abaissant, font tourner, par l’intermédiaire de poulies et de cordons enroulés en des sens concordants, un tambour (fig. 7) qui entraîne, au moyen d’un axe vertical, un agitateur à palettes dans un calorimètre plein d’un liquide quelconque et thermiquement bien isolé. D’autres palettes, fixées à la paroi du vase, rendent très grand le frottement produit dans le liquide par la rotation de l’agitateur, en sorte que les poids prennent bientôt une vitesse limite uniforme et, après avoir descendu de quelques mètres, atteignent leur niveau inférieur avec cette vitesse qui est très faible. La température du système calorimétrique aura alors monté, et notre connaissance des chaleurs spécifiques permettra de savoir combien
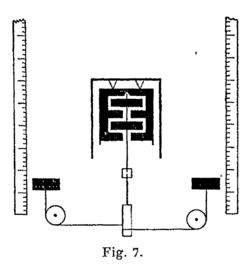
de calories il fournirait en revenant par refroidissement à son état initial. Ces calories sont achetées par l’abaissement des poids qui, pratiquement^[2] n’a pas d’autre répercussion. Le changement global constitué par l’abaissement du poids et par l’échauffement du calorimètre de Joule est donc, par définition, « isolable ». De façon générale, nous appellerons « changement de Joule » tout changement isolable où un travail et un changement thermique se conjuguent, c’est-à-dire épuisent exactement leurs effets l’un par l’autre.

27. Équivalence des enchaînements entre changements mécaniques et thermiques. — On trouve dans l’expérience de Joule que chaque kilogramme abaissé de 1 mètre engendre environ 2,33 calories, ou, si on préfère, qu’il faut 428 kilogrammètres pour échauffer 1 kilogramme d’eau de 1°, c’est-à-dire pour engendrer 1000 calories. Ou encore, en nous rappelant (V, 7) que 1 erg est le travail accompli par 1 dyne déplaçant son point d’application de 1 centimètre, qu’il faut $4,18.10^{7}$ ergs pour engendrer 1 calorie. Ceci, en changeant de toute façon imaginable les conditions de l’expérience. Par exemple, on retrouve ce résultat en forçant de l’eau à filtrer au travers d’un piston poreux chargé de poids, qui s’abaisse lentement pendant que l’eau s’échauffe par le fait de ce frottement, et sans que rien d’autre se produise.

Bref, quel que soit le genre de l’enchaînement entre un changement mécanique et un changement thermique, on retrouve toujours prix égal pour résultat égal : il y a équivalence des enchaînements possibles, comme entre changements mécaniques et comme entre changements thermiques, ou encore :

Aucun dispositif n’est plus avantageux qu’un autre pour acheter de la chaleur avec du travail.

C’est cela qui permet de parler de l’« équivalent mécanique de la calorie » (ou de l’équivalent thermique du kilogrammètre).

28. Premier principe de la thermodynamique. — Au point où il vient de parvenir, le lecteur n’aura qu’à se rappeler les principes partiels successivement atteints sur l’équivalence des enchaînements — entre travaux moteurs ou arrêts de mobiles avec travaux résistants ou lancements de mobile, — entre changements thermiques ou chimiques avec changements thermiques, — et, enfin, comme on vient de voir, entre travaux moteurs (ou arrêts de mobiles) avec changements thermiques, — pour ne pas hésiter sur la généralisation à tous changements efficients.

Nous allons ainsi admettre, sans en donner d’autres raisons, et sauf désaccord avec l’expérience, qui ne s’est jamais produit, le Principe général d’Équivalence des mécanismes d’enchaînement entre changements efficients, que nous énoncerons comme il suit :

Si deux changements efficients peuvent être conjugués au moyen d’un certain dispositif, il est impossible de réaliser un autre dispositif plus avantageux ou moins avantageux qui conjuguerait avec un de ces changements d’abord l’autre, et, en surplus, un autre changement efficient, positif ou négatif.

Il reste d’ailleurs possible qu’un autre dispositif enchaîne, avec le changement isolable constitué par les changements efficients que le premier dispositif conjuguait, un autre changement par ailleurs isolable, tel qu’un changement de Joule : cela ne réalise aucun bénéfice par rapport au premier dispositif.

Il n’est pas non plus en opposition avec notre Principe qu’un autre dispositif puisse conjuguer, avec le changement isolable constitué par les deux changements efficients conjugués par le premier dispositif, un changement instable (14) qui peut disparaître sans répercussion. Par exemple, au lieu de conjuguer par frottement, comme dans l’expérience de Joule, un abaissement de poids avec une fusion de glace, on peut les conjuguer en comprimant sous un piston de plus en plus chargé, une masse gazeuse dans un corps de pompe
Fig. 8. plongé dans un thermostat à glace fondante (fig. 9). La glace fond en même proportion que dans l’expérience de Joule, mais, en outre, le volume du gaz est réduit. Ce dernier changement peut disparaître sans répercussion, par détente de Gay-Lussac (13), ou avec une répercussion pouvant elle-même disparaître sans répercussion (14). En aucun cas, il n’est obtenu de bénéfice ou perte sous forme de changement efficient positif ou négatif.

Le Principe d’Équivalence va nous permettre d’acquérir la notion d’Énergie. Mais d’abord nous devons comprendre comment, en conséquence de ce Principe, les changements efficients peuvent être tous mesurés, en définitive parce que, de proche en proche, un changement efficient de n’importe quelle sorte peut soit acheter, soit remplacer un changement de n’importe quelle autre sorte.

---

1. Par exemple en faisant passer dans le fil un courant qui le volatilise brusquement.
2. Le travail qui serait nécessaire pour communiquer aux poids la vitesse qu’ils prennent dans l’expérience, est en général inférieur au millième du travail dépensé. La correction relative aux échauffements qui se produisent autour des axes non plongés dans le calorimètre est plus importante. On peut mesurer ensemble ces deux corrections comme il suit :

   Après avoir déclaveté l’axe qui solidarisait l’agitateur au tambour, on enroule en sens contraire les cordons tenseurs sur ce tambour, de façon que les poids s’équilibrent. L’un de ces poids étant à son niveau inférieur et l’autre à son niveau supérieur, on détermine le mouvement par une petite surcharge telle que la vitesse, bientôt rendue uniforme par les frottements sur les axes, soit ce qu’elle était dans la première expérience : l’abaissement du poids additionnel mesure le faible changement correspondant, que l’on ajoutera à celui trouvé dans le calorimètre.