OGIVE, s. f. Augive. On donne, assez improprement, le nom d’ogive à la figure formée par deux arcs de cercle se coupant suivant un angle quelconque[1]. Beaucoup de pages ont été écrites sur l’origine de ce mot, et l’esprit de parti (parti dans les questions d’art s’entend) s’en mêlant, on en est venu à si bien embrouiller la matière que toute conclusion semble avoir été ajournée à des temps plus calmes. Nous déclarons tout d’abord que nous n’avons pas la prétention de donner ici une solution, qui d’ailleurs importe assez peu ; il nous suffira de fournir à nos lecteurs les renseignements que nous avons pu recueillir sur l’adoption de cette figure dans l’architecture, à dater du XIIe siècle en France, renseignements dont on peut vérifier l’exactitude sur les monuments eux-mêmes. Quant à la conclusion, nous laisserons à chacun le loisir de la tirer.
Le compas étant inventé, les intersections de cercles étaient trouvées, par conséquent la figure appelée ogive. Ce n’est donc pas l’origine de la figure qu’il importe de rechercher, mais l’origine de son application à la construction. Des monuments de l’Asie, de la Grèce et de l’Italie, d’une très-haute antiquité, nous montrent des ogives, c’est-à-dire des berceaux ou des cavités (comme celle du trésor d’Atrée, par exemple), dont la section est donnée par deux arcs de cercle se coupant ; mais tous ces monuments, sans exception, présentent un appareil horizontal, c’est-à-dire que les lits des pierres formant ces berceaux ou ces cavités sont horizontaux et non point normaux aux courbes. C’est là cependant un point essentiel, pour des architectes, car on ne peut ainsi donner à ces surfaces concaves les noms d’arc ou de voûte. Laissons donc cette origine qui ne nous apprend qu’une chose, savoir que, lorsqu’il s’est agi de fermer un passage ou une salle, on a donné, pendant les époques primitives dont nous parlons, des formes diverses aux encorbellements, seuls moyens admis pour arriver à ce résultat. Retraites, plans inclinés, courbures, ce sont toujours des encorbellements et non des voûtes, et la forme ogivale n’est alors qu’une fantaisie du constructeur, non un système. Les Étrusques, qui ont fait de véritables arcs appareillés, c’est-à-dire composés de claveaux dont les coupes sont normales à la courbe, et les Romains qui ont fait des arcs et des voûtes en berceau d’arêtes et en calotte hémisphérique, n’ont jamais adopté l’ogive, ou s’ils l’ont fait, ce sont des exceptions trop rares pour qu’on en puisse tirer une conclusion. Les Romains n’ont admis qu’une courbe génératrice de la voûte, c’est le demi-cercle, ce qu’on appelle le plein-cintre ou l’arc de cercle, cintre incomplet. D’Auguste à Constantin, pas d’exception à cette méthode. Ce n’est guère qu’au VIe siècle que nous voyons poindre l’ogive sur les bords de la Méditerranée, en Égypte, au Caire ; et là, elle apparaît déjà comme le résultat d’un calcul. Dans un autre ouvrage, nous avons expliqué d’une manière détaillée comme quoi les anciens se sont servis du triangle pour mettre en proportion leurs édifices[2] ; comment parmi les triangles ils en avaient adopté trois : 1o le triangle équilatéral ; 2o le triangle pris verticalement sur la diagonale d’une pyramide à base carrée, dont la section verticale, faite du sommet parallèlement à l’un des côtés de la base, est un triangle équilatéral ; 3o le triangle dont la base est quatre et la hauteur, prise perpendiculairement du milieu de cette base au sommet, est deux et demi. Ces trois triangles donnent au sommet un angle de moins de 90º ; donc il n’est pas possible de les inscrire dans un demi-cercle.
Le triangle équilatéral (voir figure 1, en B) est aussi un générateur de l’ogive ; mais ce n’est que beaucoup plus tard qu’on l’emploie, tandis que le triangle pris sur la diagonale d’une pyramide à base carrée, dont la section verticale, faite du sommet parallèlement à l’un des côtés de la base, donne un triangle équilatéral, est adopté très-anciennement pour tracer l’arc brisé. Soit fgh la moitié de la projection horizontale d’une pyramide à base carrée, dont la section verticale faite sur ik est un triangle équilatéral ; la section verticale faite sur la diagonale fh donne le triangle fhl. Élevant une perpendiculaire mn sur le milieu d’un des côtés hl de ce triangle, le point de rencontre n de cette perpendiculaire avec la base fh donnera le centre de l’arc hol. Traçant du point l, comme sommet, un angle égal à l’angle l′fg, de manière à ce que la ligne lp sépare cet angle en deux angles égaux, nous avons les deux côtés lq, lr, d’un triangle équilatéral quelconque ; prolongeant le tracé des arcs loh jusqu’à leur rencontre avec ces côtés lr, lq ; qrl est un triangle équilatéral dont les côtés ql, rl sont les cordes des arcs lor, lo′q. L’arc brisé qrl est outre-passé ; il donne au plus grand écartement fh, entre les deux arcs, la proportion du triangle fhl, et, à sa naissance qr, la proportion du triangle équilatéral qrl. Le nu des pieds-droits de cet arc sera en s et t, c’est-à-dire à l’aplomb des deux points f, h. Cette forme d’arc outre-passé, employée fréquemment dans les monuments de la Perse, se trouve déjà adoptée pour la construction des portiques de la mosquée d’Amrou au Caire, construite en 640 environ, avec quelques variantes dans la méthode du tracé. Mais les architectes de l’école d’Alexandrie, et les artistes grecs, initiateurs des populations d’Orient après le Ve siècle, n’avaient fait autre chose que de donner à l’arc brisé un tracé méthodique, en vue de satisfaire à un sentiment délicat des proportions. Bien que dans la construction de ces arcs, les joints des claveaux fussent normaux aux courbes, tendissent aux deux centres, ainsi qu’on le voit en X[5] ; que, par conséquent, la structure fût d’accord avec la forme, et que ces arcs brisés fussent plus résistants que l’arc plein-cintre, tout en exerçant une poussée moins grande, cependant les architectes orientaux n’avaient pas entrevu d’autre application de cette forme nouvelle, le système des voûtes n’était pas pour cela modifié. Il était réservé aux architectes du nord de la France de s’emparer de l’arc brisé et d’en faire le point de départ d’une structure neuve, d’un art original.
Sur les arcs brisés ou plein-cintre (car les Orientaux les employaient simultanément, quoique cependant l’arc brisé persiste au Caire et en Perse plus que partout ailleurs), on élevait dans tout l’Orient des pendentifs et des calottes sphéroïdales, comme dans les premiers temps de l’empire de Byzance, sans chercher à tirer de cette nouvelle forme d’arcs des conséquences de nature à modifier la construction des voûtes. Avec ce génie inventif et pratique qui distingue les peuples de l’extrême occident, nos architectes, dès le commencement du XIIe siècle, c’est-à-dire après les premières croisades, s’emparèrent de l’arc brisé et en firent rapidement une application fertile en résultats. Jusqu’alors, en France, on ne connaissait que la voûte romaine et on s’évertuait à la transformer sans obtenir autre chose que de grossières tentatives accusant un désir de satisfaire à de nouvelles nécessités bien plutôt qu’un progrès. Ne construisant plus en blocages, rarement en brique, la voûte d’arête romaine n’était fermée qu’à la suite de difficultés nombreuses, qu’à l’aide de tâtonnements. Les arêtes saillantes de la voûte romaine moulée sur forme, lorsqu’on voulait les construire en moellon, n’offraient pas de solidité ; on rehaussait les clefs, on cherchait un compromis entre cette forme de voûte et la coupole, afin de donner le moins de saillie possible à ces arêtes[6] que l’on ne savait comment maintenir entre les portions de cylindre ou de conoïdes poussant au vide. On tendait toujours vers la coupole et l’on cherchait, au moyen de cintres permanents, d’arêtes appareillées, dès le commencement du XIIe siècle, à maintenir les lobes des voûtes. Ces arêtes appareillées (arcs diagonaux, arcs ogives) étaient déjà un grand pas de fait.
Les Clunisiens, qui dès le XIe siècle étaient maîtres en l’art de bâtir, et qui avaient formé une école d’architecture déjà brillante à cette époque, furent les premiers qui surent appliquer l’ogive à la construction, non-seulement des arcs mais des voûtes[7]. En relations constantes avec l’Orient, ils en rapportèrent l’arc brisé ; mais ce ne fut que sur le sol français que cet arc détermina une révolution dans l’art de la construction.
En effet, tous les monuments clunisiens et cisterciens bâtis en Palestine avant le XIIIe siècle, et si complètement décrits par M. le comte Melchior de Vogué dans son ouvrage sur la Terre Sainte[8], en adoptant l’ogive pour les arcs, conservent cependant le système de la structure romane, et dans aucun de ces édifices l’ogive n’intervient pour modifier la voûte d’arête romaine, en berceau, ou la coupole. Mais sitôt introduite dans les provinces françaises au nord de la Loire, l’ogive se mêle à la voûte et la modifie. Voici d’abord comment le mélange se fait.

Le principe admis, les conséquences allaient s’ensuivre avec une prodigieuse rapidité. Le grand embarras, pour les architectes romains, n’était pas de faire des voûtes sur plan carré, mais sur plan barlong. Les Romains, dans ce cas, avaient fait des berceaux avec pénétration ou des voûtes d’arêtes trichées, c’est-à-dire engendrées par deux cylindres de diamètres différents se pénétrant ; les cylindres du plus faible diamètre ayant leur naissance au-dessus de celle des cylindres de grand diamètre, ce qui produit un très-mauvais effet. Mais dès que la coupole devenait le point de départ de toute voûte, ces embarras devaient disparaître. Nous avons expliqué, figure 2, comment d’une calotte hémisphérique on pouvait faire une voûte d’arête sur plan carré, en substituant aux sections semi-circulaires données par des plans verticaux élevés sur les côtés du carré inscrit, des arcs brisés ou des ogives. Les conséquences de cette innovation ne se firent pas attendre.

Une difficulté, purement matérielle et minime en apparence, obligea bientôt les architectes à faire de nouveaux progrès dans le tracé des voûtes et à étendre les applications de l’arc brisé. Vers la fin du XIIe siècle on commençait des édifices religieux et civils d’une dimension inusitée jusqu’alors. On portait la largeur des grandes nefs jusqu’à quinze et seize mètres et même jusqu’à vingt[12]. L’art de l’architecture était alors exclusivement tombé entre les mains des laïques, et ceux-ci comprirent bientôt tout le parti qu’ils pouvaient tirer du nouveau système de voûtes. Avec cette logique qui distingue l’habitant des Gaules, les maîtres des œuvres reconnurent que, puisque de la coupole on ne conservait plus que deux diagonales, ou deux sections faites sur les diagonales d’un parallélogramme inscrit dans le cercle, base de cette coupole, il fallait franchement donner à ces deux arcs croisés une fonction utile, indispensable ; il fallait en faire l’ossature de la voûte et porter sur cette ossature des voûtains indépendants les uns des autres, pouvant ainsi s’incliner en tous sens, se biaiser, s’allonger, devenir très-concaves ou presque plats. Les voûtes des cathédrales de Paris, de Senlis, celles de beaucoup d’églises de l’Île de France bâties de 1160 à 1200, présentent déjà une quantité de combinaisons qui indiquent combien, en très-peu d’années, l’école laïque s’était émancipée, tout en conservant le principe primitif issu de la coupole et de l’arc brisé. Cependant, — car si rapidement que l’on progresse, il y a toujours entre le point de départ et le point d’arrivée des transitions, — la coupole considérée comme génératrice est une tradition si puissante, que pour la construction des grandes voûtes, les architectes n’osent pas encore se fier entièrement aux conséquences du système que nous venons d’indiquer. Ils ont encore dans l’esprit la configuration de la coupole, ils tâtonnent.
Les hautes voûtes du chœur de la cathédrale de Paris, qui étaient terminées avant l’année 1190, nous fournissent à cet égard un sujet d’études intéressantes. La date de leur construction est certaine, et elles n’ont pas été modifiées plus tard ainsi que cela est arrivé pour la plupart des absides du XIIe siècle.
Le souvenir de la coupole a évidemment inspiré le tracé de ces voûtes (6).
De tout ceci il résulte que les arcs ogives BG, FD, F6, G3, et les branches 4E, 5E sont bien réellement des côtes de coupoles entre lesquelles on a percé des formerets et des arcs doubleaux affectant la courbe aiguë. Les architectes n’osaient même encore s’affranchir de la configuration concave de la coupole, bien que le système admis l’eût permis, car ils avaient le soin de tenir les clefs des arcs doubleaux et des formerets plus basses que celles des arcs diagonaux, afin de conserver à la structure cette forme de calotte qui leur semblait nécessaire à la solidité.
Le principe de la coupole considérée comme génératrice des voûtes en arcs d’ogives nous paraît trop important pour que nous n’insistions pas.
Les projections des grandes voûtes du chœur de la cathédrale de Paris que nous avons tracées (fig. 6) nous montrent en BDFG une voûte presque carrée, composée de deux arcs ogives BG, DF, de deux arcs doubleaux BD, FG, d’un arc doubleau intermédiaire KI et de quatre formerets BK, KF, DI, IG. Ayant la disposition des voûtes sur plan carré des collatéraux, des points d’appuis en B, K, F, D, I, G d’une part, et la tradition de la coupole de l’autre, les constructeurs, cherchant à conserver de cette coupole deux tranches diagonales BG, DF, sur lesquelles devaient reposer les remplissages ou voûtains, ne pensaient pas que ces diagonales dussent ne point se couper suivant des angles très-rapprochés de l’angle droit, sinon droits. Ils franchissaient ainsi deux travées, faisant porter ces arcs ogives ou diagonaux sur les points d’appuis, de deux en deux ; mais autant pour diminuer la surface des remplissages que pour répartir leur poids sur toutes les piles, ces constructeurs recoupaient la voûte en arcs d’ogives par un arc doubleau intermédiaire KI.

Voici donc ce que donnait cette combinaison (8). La coupole à projection horizontale circulaire était encore la génératrice de cette voûte. En effet (voir la projection horizontale A), les arcs ogives ab, cd, ne sont autre chose que les tranches réservées de la coupole ; seulement, les murs de la nef étant sur les deux parallèles ad, cb, un arc doubleau intermédiaire bandé de la pile e à la pile f permettait de voûter chacun des triangles adg, cbg au moyen de deux voûtains aeg, edg, cfg, fbg. Au lieu de deux formerets ad, cb, on obtenait quatre formerets ae, ed, cf, fb. Le figuré perspectif B explique ce système. Là, le plan fictif de la coupole est visible. Les deux arcs ogives CD, EF en sont les dernières traces ; l’arc doubleau intermédiaire GH, au lieu d’être, comme les arcs ogives, une tranche séparée de la coupole, a été reporté de G′ en G et de H′ en H ; son sommet atteint le niveau de la clef I des arcs ogives ; puis, l’ossature ainsi établie, dans les triangles K restés vides on a bandé les voûtains K′, qui portent sur les arcs ogives, les arcs doubleaux, et qui sont tracés par les formerets L. Ce système offrait encore l’avantage de prendre des jours latéraux sous les formerets dans la hauteur même de la voûte.
Mais il était peu logique, ayant des points d’appuis égaux en force, en aed, de faire porter deux arcs ogives et un arc doubleau sur les piles ad, tandis qu’on ne chargeait la pile e que d’un seul arc doubleau. On prit donc, vers 1230, le parti de faire des grandes voûtes par travées, très-barlongues, et de charger également toutes les piles. C’est ainsi que sont construites les voûtes hautes des nefs des cathédrales d’Amiens et de Reims ; la coupole en est cependant le principe générateur comme pour les voûtes précédentes. Dans la cathédrale d’Amiens les arcs diagonaux ou ogives sont des plein-cintres, ou très-peu s’en faut ; mais dans celle de Reims la coupole génératrice des arcs ogives est tracée sur un triangle équilatéral, et l’épure de ces voûtes est aussi simple que profondément raisonnée.



Soit en B l’arc brisé auquel le nom de tiers-point doit être appliqué de préférence à tout autre, la base ce étant divisée en trois parties égales, cette base pourra être divisée en six parties égales, et la perpendiculaire abaissée du sommet de l’arc sur la base divisera celle-ci en deux parties égales ; donc le rayon fe ayant quatre de ces parties, le rayon fg en contiendra également quatre. Or, supposons que pour tracer l’épure des claveaux de l’arc brisé B nous n’ayons que l’espace fBg, la base ce étant connue, nous en prendrons le sixième que nous tracerons en B′f′ (voir le figuré C) ; sur la base B′f′, du point B′ nous élèverons une perpendiculaire B′g′ ; prenant alors un rayon f′g′ ayant quatre fois la longueur de B′f′ qui est le tiers du demi-diamètre de l’arc, et posant la pointe du troussequin en f′, la rencontre de la ligne f′g′ avec la perpendiculaire B′g′ donnera le point g′, sommet de l’arc brisé. Nous pourrons tracer une portion d’arc g′i, donner l’épaisseur des claveaux iK et tracer les joints d’un de ces claveaux. Tous les claveaux de l’arc seront donc donnés par celui lmno, et nous pourrons, sur ce panneau, en faire tailler des milliers. Reste à tracer la clef ou plutôt la contre-clef, puisque les arcs brisés ont un joint à la clef. Le prolongement de la perpendiculaire B′g′ nous donnera le panneau de cette contre-clef, comme l’indique notre figure. Mais nous avons encore un autre moyen d’obtenir son panneau (voir le tracé D). Soit la ligne pq l’épaisseur des claveaux, nous la divisons en quatre parties ; traçant du point q, au moyen d’une sauterelle, un angle qrs égal à l’angle f′ut, nous prendrons sur le côté qs une longueur qv égale à l’une des quatre parties de la ligne d’épaisseur pq ; nous réunirons le point p au point v, et nous aurons tracé le triangle pqv à ajouter aux claveaux pour former le panneau de la contre-clef. Pour tracer les panneaux des claveaux de l’arc quinte-point figuré en G, on procèdera de la même manière ; seulement, la base de l’arc étant divisée en cinq parties égales, nous prendrons une de ces parties et demie pour commencer l’opération et nous en prendrons quatre pour le rayon. Ce n’était donc pas au hasard que les constructeurs du moyen âge, dans le tracé de leurs arcs brisés, posaient les centres sur la ligne de base ou de naissance de ces arcs, et comme preuve de leur méthode de tracé d’épures partielles, on peut observer que les claveaux ayant été taillés sans connaître exactement le nombre nécessaire à chacune des branches de l’arc, ou la largeur de douelle, il arrive souvent qu’au moment de fermer l’arc, on pose une contre-clef très-large ou un dernier claveau beaucoup plus mince que les autres.
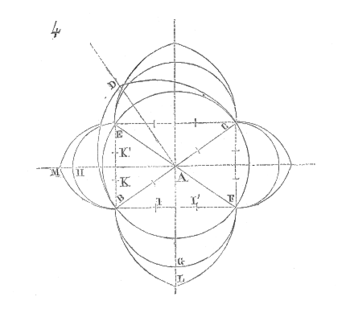
Mais une figure singulière, tracée dans l’Album de Villars de Honnecourt, nous donne la clef de tout un système de tracés d’arcs pour un édifice entier et permettant, comme dans l’exemple précédent, de faire des épures partielles avec une rigoureuse exactitude et sans avoir besoin d’aires d’une surface considérable[16]. La planche XXXIX de cet album nous montre une clef de tiers-point tracée d’après la méthode précédente, puis une spirale coupée par une ligne droite passant par son œil. Au-dessous de ce croquis, on lit : « Par chu tailon one clef del quint point » (Par ce moyen taille-t-on une clef de quinte-point). Le texte ne se rapporte qu’au trait de la clef, mais la présence de cette spirale, dessinée là comme un simple souvenir, se rapporte évidemment aux tracés d’arcs engendrés par une division du diamètre en cinq. Ce croquis est celui reproduit exactement par le trait plein de notre figure 12[17].

Sur une base AB, divisée en cinq parties égales et donnant six points, du milieu C comme centre on a tracé le demi-cercle AB. — On observera que ce point C sépare la division 3−4 en deux parties égales. — Prenant alors le point 3 comme centre et 3A comme rayon, on a tracé le second demi-cercle A5. Reportant la pointe du compas sur C et prenant C5 comme rayon, on a tracé le troisième demi-cercle 2−5. Reportant la pointe du compas sur 3 et prenant 3−2 comme rayon, on a tracé le quatrième demi-cercle 2−4. Reportant enfin la pointe du compas sur C et prenant C4 comme rayon, on a tracé le cinquième demi-cercle 3−4. Si des deux centres 3 et C, qui ont servi à tracer tous les demi-cercles, nous élevons les deux perpendiculaires 3a, Cb, nous coupons ces demi-cercles en a, en c, en b et en d. En supposant que les arcs ogives d’une grande voûte barlongue de nef soient le plein-cintre dont AB est le diamètre, les arcs doubleaux ayant une base comprenant quatre parties ou la longueur A5, ces arcs doubleaux se composeront d’une branche d’arc Aa et d’une seconde branche d’arc 5a dont le centre sera e point milieu de la partie 2−3. L’arc doubleau sera tracé au moyen de deux arcs de cercle dont le rayon sera CA et dont les centres Ce seront des points diviseurs du diamètre A5 en huit parties égales. Le diamètre de l’arc ogive ayant cinq parties et l’arc doubleau quatre (voir la projection horizontale H), l’arc formeret aura trois parties, car l’arc formeret lm formant un angle droit sur l’arc doubleau ln, si nous donnons à la base de cet arc doubleau 4, à la base de l’arc formeret 3, l’hypoténuse mn, ou base d’un des arcs ogives, aura 5 par la raison que le carré de 4 est 16, le carré de 3, 9, que 16 + 9 = 25 carré de 5. Donc AB étant la base de l’arc ogive d’une voûte dont l’arc doubleau est A5, le formeret aura pour base 3B comprenant trois parties, et nous aurons tracé l’arc ogive de cette voûte, son arc doubleau et son arc formeret avec la même ouverture de compas ; les points diviseurs de la base AB nous ayant donné en C le centre des arcs ogives, en Ce les centres de l’arc doubleau, en Cf les centres de l’arc formeret. Par conséquent, les mêmes arcs de cercle servant pour tracer ces trois arcs, tous les panneaux des claveaux de ces arcs pourront être taillés sur une seule épure ou portion d’épure, en supposant que nous appliquions le procédé indiqué en D (11). Si c’est une voûte plus étroite que nous voulions tracer, c’est-à-dire une voûte dont la base des formerets soit la moitié de la base de l’arc doubleau, nous aurons alors en projection horizontale le tracé lpqn (voir le figuré H). Alors l’arc ogive np aura pour diamètre 4 parties 1/2. Cet arc ogive sera donc la courbe brisée dont le diamètre est Af et dont les centres sont les points 3 et C. L’arc doubleau aura pour diamètre comme précédemment A5 et pour points de centre eC, et l’arc formeret aura pour diamètre soit 2−4, soit 3−5, et pour points de centre soit eC, soit ef : dans le premier cas cet arc formeret sera tracé avec une ouverture de compas plus courte que celle qui a servi à tracer l’arc ogive et l’arc doubleau ; dans le second, il sera tracé avec la même ouverture de compas. Si nous divisons le tympan sous l’arc formeret en deux baies jumelles, chacune aura une partie de la base AB soit 3−4 ; et le centre de chacun de ces arcs dont la clef est d sera en 3 et en 4, cet arc sera équilatéral. Si l’arc formeret de la voûte barlongue lnmr, ayant pour base 3B et pour centres C f, nous paraît trop aigu, nous pouvons lui substituer l’arc dont la base est 2−5, dont la clef est b et dont les centres sont 3−4. On comprend donc qu’à l’aide de cette figure, les bases de tous les arcs de la voûte donnant toujours des divisions égales connues ainsi que les rayons de ces arcs, ils peuvent être taillés à l’aide d’une épure partielle prenant très-peu de surface. Et en effet, si nous examinons des églises gothiques bâties pendant le XIIIe siècle, nous reconnaissons que tous les arcs ogives, doubleaux, formerets, que les archivoltes, travées de galeries, etc., sont tracés au moyen de points de centres posés sur des divisions égales en cinq ou dix d’un seul diamètre de cercle. Il ne nous paraît pas nécessaire d’insister davantage sur l’importance de la figure spirale contenue dans l’Album de Villars de Honnecourt, mais il n’est pas hors de propos de faire remarquer que la voûte barlongue lnmr, dont la projection horizontale est tracée en H, dérive du triangle donné par Plutarque comme étant le triangle parfait des Égyptiens, et que l’arc doubleau, dont le diamètre est A5 divisé en quatre, possède une flèche 3a divisée en 2 1/2 moins une très-minime fraction, c’est-à-dire qu’il inscrit un triangle à très-peu près semblable à celui que donne la section verticale de la grande pyramide de Chéops. L’arc dit ogive mérite donc quelque attention : ce n’est pas seulement un motif de solidité qui l’a fait adopter, mais aussi un sentiment des proportions et un accord harmonique entre toutes les courbes des voûtes ; c’est une nécessité résultant de la pratique dans le tracé des épures ; c’est surtout un besoin de liberté dans la construction de ces voûtes dont on ne saurait trop étudier à fond le principe excellent, puisqu’il permet toutes les combinaisons.
Depuis vingt ans on a fait beaucoup de pastiches de la structure gothique ; bien rarement ces imitations satisfont les yeux : c’est qu’en effet ceux qui les élèvent, en admirant fort d’ailleurs nos anciens monuments, ne se sont probablement pas donné la peine d’en rechercher les savants et judicieux éléments. En architecture, le goût, le sentiment sont beaucoup ; mais pour les appuyer il faut nécessairement se servir du compas et de la géométrie. On voit qu’au moyen de la formule (12) il n’est qu’un des arcs brisés qui ait ses centres en dehors de ses naissances.
C’est qu’en effet dans ces belles écoles de l’Île-de-France, de la Champagne, du Soissonnais, les architectes, gens de goût, avaient senti que la dernière limite d’aiguité de l’ogive était l’arc équilatéral ; que les centres des branches d’arc placés en dehors des naissances donnaient une brisure dont l’extrême aiguité était choquante, une proportion désagréable, en ce que les rapports de la base avec la hauteur outrepassaient le triangle équilatéral (voy. Proportion ). Mais les Normands, les Anglo-Normands étaient moins délicats et cherchaient dans leur structure, avant toute chose, les formules qui supposent des moyens pratiques simples. Aussi, au lieu de tenter, comme dans la figure 12, de trouver des arcs brisés de diamètres différents ayant tous des angles égaux au sommet ou du moins peu dissemblables, des rapports analogues entre les diamètres et les flèches, ces gens pratiques du Nord, bons constructeurs dès le commencement du XIIe siècle, se préoccupent médiocrement des rapports proportionnels, du choix des formes : ils veulent une méthode expéditive. Nous avons vu comme Villars de Honnecourt donne les moyens de tracer un plein-ceintre et plusieurs arcs brisés « avec la même ouverture de compas. » Or, les voûtes normandes élevées vers 1220 présentent souvent une disposition telle que tous les arcs, arcs ogives, arcs doubleaux, formerets, archivoltes, sont tracés à l’aide d’un même rayon.

Ainsi (13), soit la projection horizontale d’une de ces voûtes, l’arc générateur est l’arc ogive qui est un plein-cintre rabattu en ABC. L’arc doubleau AC rabattu en ACS est tracé au moyen du rayon ab égal au rayon OC. L’arc doubleau de recoupement des arcs ogives DE rabattu en DEF est tracé de même, au moyen du rayon ef égal au rayon OC, sa clef F étant naturellement au niveau C de la clef des arcs ogives. Soit iK, lm, l’épaisseur des piles, les arcs formerets étant compris entre Kl. Ces arcs formerets rabattus en Klp sont encore tracés au moyen du rayon rt égal au rayon OC, leur naissance étant relevée de K en V si l’on veut que les clefs des formerets atteignent le niveau des clefs des arcs ogives. Si ces formerets servent d’archivoltes aux baies divisées par un meneau, ce sera encore le rayon nq égal au rayon OC qui servira à tracer les arcs diviseurs de la fenêtre.
Sauf pour les clefs, l’épure d’un seul claveau d’arc suffisait alors pour tailler les panneaux de tous les arcs des voûtes, archivoltes, baies, etc. Et (voir le tracé G), si nous divisons un diamètre d’arc ogive en quatre ou en dix, avec la même ouverture de compas, nous pourrons avoir une suite d’arcs dont les diamètres seront au diamètre du plein-cintre, qui est le plus grand arc de la voûte ou l’arc ogive, comme trois, deux, un sont à quatre, ou comme neuf, huit, sept, six, etc., sont à dix. Ayant donc des claveaux tous taillés sur un même arc, et une base ou fraction de base, nous pouvons, sans épure, monter tous les arcs d’un édifice. On comprend alors le motif qui avait fait adopter l’arc brisé que l’on appelle lancette : c’était une économie de tracé, on évitait toute complication d’épures et de panneaux, il ne s’agissait plus que de donner la section de chacun de ces arcs suivant leur fonction. Tous taillés d’ailleurs sur une même courbure (à l’extra-dos), ils prenaient leur place suivant la désignation donnée. S’il fallait des épures, c’était seulement pour les cintres en charpente, et encore ces arcs étant tous tracés à l’aide d’un même rayon, l’épure du demi-cercle ou de l’arc ogive permettait de mettre sur ligne tous les autres cintres, puisqu’il suffisait de savoir quel était le rapport existant entre les diamètres de ces arcs et celui du demi-cercle pour avoir le tracé complet de chacun d’eux, ainsi que le fait voir la figure 13 en G[18].
De ce qui précède on peut conclure : 1o que l’arc brisé, appelé ogive, a été d’abord une importation d’Orient ; 2o qu’adopté en Orient comme une courbure donnée par un principe de proportion expliqué ailleurs[19], cet arc brisé a été en France le point de départ de tout un système de construction parfaitement logique, et permettant une grande liberté dans l’application ; 3o que par conséquent l’arc brisé, comme forme, appartient probablement à l’école d’Alexandrie et aux Nestoriens, qui paraissent les premiers l’avoir adopté ; mais que, comme principe d’un nouveau système de voûtes, il appartient sans aucun doute à nos provinces du nord de la Loire, puisqu’en 1140, dans l’église abbatiale de Saint-Denis, les constructions élevées par Suger ne laissent apparaître les plein-cintres que pour les arcs ogives, et qu’elles ont appliqué déjà le système de voûtes que nous voyons se développer dans la cathédrale de Paris vingt ans plus tard. Or, nulle part, ni en Europe, ni en Orient, au milieu du XIIe siècle, on ne construisait de voûtes ayant quelques points de rapports, comme emploi de l’arc brisé, avec celles de l’église de Saint-Denis et de la cathédrale de Paris. Si donc l’arc brisé a pris naissance hors de France comme forme d’arc, nous sommes les premiers qui ayons su l’appliquer à l’une des plus fertiles inventions dans l’histoire de la construction. Si donc l’arc brisé a pris naissance hors de France, nous sommes les premiers qui ayons su tirer de cette forme, issue d’un sentiment des proportions[20], des conséquences d’une valeur considérable, puisqu’elles ont produit la seule architecture originale qui ait paru dans le monde depuis l’antiquité.
- ↑ Croix d’augives, au commencement du XIVe siècle, s’entendaient pour les arcs diagonaux d’une voûte d’arête gothique. Or, ces croix d’augives, ou arcs ogives, sont le plus souvent des pleins-cintres. « Item II. crois d’augives pour faire les voûtes sus et une arche entre II crois augivères… ». (Titre de fondation d’une chapelle à Averdoin, du mois de juin 1347. Archives de M. le duc de Luynes… — Voy. t. II des Annales archéologiques, p. 41, l’article de M. Lassus sur l’arc ogive.) Pendant le moyen âge, et jusqu’au XVIe siècle, le mot ogive ou augive, arcs ogives, ne s’appliquait qu’aux nervures croisées. Les autres arcs, fussent-ils aigus, s’appelaient arc doubleau, tiercerons, formerets. (Voy. les articles arc, Construction.)
- ↑ Voyez le Neuvième Entretien sur l’Architecture.
- ↑ Traité sur Isis et Osiris.
- ↑ Voyez le Neuvième Entretien sur l’Architecture.
- ↑ Les Italiens n’ont jamais compris les raisons qui avaient fait adopter la forme de l’arc brisé au point de vue des proportions et de sa véritable fonction. On peut en avoir la preuve si l’on observe que presque tous leurs arcs brisés sont appareillés comme un plein-cintre, c’est-à-dire que les joints des claveaux tendent à un seul centre, ce qui est un contre sens ; que les proportions de ces arcs brisés présentent presque toujours un rapport de proportions désagréable entre la base et la hauteur. Mais les Italiens du moyen âge n’ont pas compris grand’chose à l’art grec postérieur au bas temps, et les Grecs le savaient, puisqu’ils les considéraient comme des barbares.
- ↑ Voyez les voûtes des bas-côtés de l’église de Saint-Martin-des-Champs, à Paris ; celles des bas-côtés de l’église de Poissy, etc.
- ↑ Les arcs doubleaux de l’église de Saint-Front de Périgueux datent des dernières années du Xe siècle, et sont déjà des arcs brisés.
- ↑ Les Églises de la Terre Sainte, par le comte Melch. de Vogué. Paris, 1860.
- ↑ Par cette raison que toute section d’une sphère par un plan donne un cercle.
- ↑ D’autres découvertes aussi simples dans leur principe que fertiles en résultats ont mis, en ce monde, bien du temps à surgir ; mais rarement on a considéré ces éclairs de l’esprit humain comme un signe de barbarie. Rarement les peuples au milieu desquels ils ont apporté une lumière nouvelle ont cherché à voiler leur éclat.
- ↑ Ces arcs diagonaux sont ce qu’on appelle, dans la construction des voûtes gothiques, les arcs ogives. (Voy. construction.)
- ↑ Nef de l’ancienne cathédrale de Toulouse.
- ↑ La Bourgogne est de quelques années en retard sur l’Île de France, et les voûtes du chœur de Vézelay correspondent comme facture à celles (anciennes) de la cathédrale de Noyon, qui date du milieu du XIIe siècle.
- ↑ Album de Villars de Honnecourt. Voir les éditions française et anglaise. Pl. XI.
- ↑ Cette dénomination nous semble en effet parfaitement applicable à cette sorte d’arc, puisque la pointe du compas est placée sur le troisième des points diviseurs de la base. Cependant l’arc équilatéral est souvent aussi appelé tiers-point. Nous allons voir pour quelle raison.
- ↑ L’usage de cette figure, qui n’a point été expliquée dans l’édition française de Villars de Honnecourt, est, en présence des monuments, d’une importance capitale. N’oublions pas que les anciens maîtres des œuvres, bâtissant dans des villes resserrées, ne pouvaient disposer de chantier ou d’aires d’une grande étendue. En théorie, on ne tient guère compte de ces difficultés, mais dans la pratique elles ont une telle importance, qu’elles forcent les architectes qui tiennent à faire tracer leurs épures devant eux à adopter des méthodes qui influent sur les formes adoptées.
- ↑ Les lignes ponctuées, chiffres et lettres ont été posés par nous pour expliquer l’usage de cette figure.
- ↑ C’est en faisant refaire des arcs de voûtes gothiques que nous avons été amené à reconnaître cette unité de la courbe pour beaucoup d’entre eux dans un même édifice, quel que fut le diamètre de chacun de ces arcs, car les courbes de cintres en charpente taillés pour l’un servaient pour plusieurs ; seulement le segment de chaque branche était plus ou moins long.
- ↑ Dans nos Entretiens sur l’architecture (Neuvième).
- ↑ Voyez le Neuvième Entretien sur l’architecture et l’art. proportion.
