Leçons sur les hypothèses cosmogoniques (Poincaré, 1911)/Chapitre 07

Henri Poincaré

Leçons sur les hypothèses cosmogoniques

Libraire scientifique A. Hermann et fils, 1911 (p. 131-189).

CHAPITRE vii.

THÉORIE DE Sir G. H. DARWIN.

---

I. — Généralités.

94.Dans l’histoire, tant passée que future, des astres du système solaire, Sir G. H. Darwin attribue un rôle essentiel à l’influence des marées^[1].

Considérons les marées produites sur une planète T par un astre troublant L (fig. 25) : la planète sera, par exemple, la Terre et l’astre
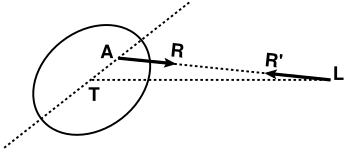
fig.25. troublant la Lune. Rendons-nous compte de l’action du frottement de la marée sur la rotation de la planète et de la réaction qui en résulte sur le mouvement de l’astre producteur de la marée. Si la théorie statique des marées pouvait être appliquée, la surface des océans terrestres serait un ellipsoïde allongé vers la Lune L. Mais les frottements dus à la viscosité ont pour effet de produire un décalage, un retard de la marée sur l’instant du passage de la Lune au méridien. Le grand axe de l’ellipsoïde terrestre fera donc un certain angle avec la ligne TL qui joint les centres de gravité des deux astres^[2]. Par conséquent, la résultante $\mathrm {R}$ des attractions de la Lune sur les molécules terrestres ne passe pas par le centre de gravité T de la Terre, mais est appliquée à un certain point A : cette résultante a donc un moment par rapport au point T et tend, par suite, à ralentir le mouvement de rotation de la Terre.

De même, l’attraction $\mathrm {R} '$ de la Terre sur la Lune n’est pas dirigée suivant le rayon vecteur LT ; ce n’est plus rigoureusement une force centrale : elle a une petite composante tangentielle qui va troubler le mouvement orbital de la Lune. Cette composante tangentielle, dirigée dans le sens même du mouvement de la Lune sur son orbite produira évidemment un effet inverse de celui d’une résistance de milieu, cette dernière étant une force tangentielle dirigée à l’opposé du mouvement orbital de la Lune. Il y aura donc augmentation du grand axe de l’orbite lunaire et, conséquemment, diminution de la vitesse angulaire de révolution.

Cette augmentation du grand axe de l’orbite lunaire pouvait encore se prévoir autrement. L’effet de freinage des marées est de diminuer la vitesse angulaire de la Terre et par suite son moment de rotation. D’autre part, le moment de rotation total du système Terre-Lune doit rester constant. Donc le moment de rotation dû au mouvement orbital de la Lune doit augmenter, c’est-à-dire que la distance de la Lune à la Terre doit s’accroître.

Nous prévoyons donc dès maintenant et sans calculs que les deux principaux effets du frottement des marées sont la diminution de la rotation terrestre et l’augmentation corrélative de la distance de la Lune. En d’autres termes, la durée du jour augmentera, ainsi que celle du mois.

95.Pour expliquer l’accélération séculaire du moyen mouvement de la Lune dont la gravitation, comme on le sait, ne paraît pas rendre entièrement compte, Delaunay avait déjà proposé d’admettre une augmentation de la durée du jour sidéral, due précisément à l’action du frottement des marées sur le fond des océans. Dans cette hypothèse, l’accélération séculaire de la Lune ne serait pas réelle ; ce ne serait qu’une apparence due à ce que notre unité de temps, le jour sidéral, augmenterait peu à peu. Bien plus, l’effet des marées, loin de produire réellement une accélération du moyen mouvement de la Lune, augmenterait au contraire la distance de cet astre à la Terre et sa période de révolution, comme nous venons de le remarquer. N’est-il pas à craindre alors que ce retard effectif ne l’emporte sur l’accélération apparente ? Pour répondre à cette objection, Delaunay soutenait que le coefficient du retard imprimé à la Lune est moindre que celui du retard de la rotation de la Terre, ce qui se trouve être exact, semble-t-il. Mais, si l’on ne tient compte que du frottement des océans actuels sur leur fond, l’effet total est tout à fait minime et insignifiant. Il faudrait supposer que l’intérieur du globe terrestre n’est pas rigide, qu’il est plus ou moins visqueux, et que, par conséquent, les marées internes y produisent des frottements intenses.

II. — L’excentricité et l’inclinaison de l’orbite lunaire sont supposées nulles.

96.Quoi qu’il en soit, et pour en revenir au point de vue cosmogonique, on doit supposer, avec Sir G. H. Darwin, que dans ses états antérieurs la Terre était fluide et visqueuse. Elle a alors subi des marées dans toute sa masse (bodily tides), et les frottements dus à ces marées internes étaient incomparablement plus énergiques que ceux qu’on peut attribuer actuellement aux marées océaniques.

97.Nous nous proposons d’étudier de plus près les variations que subissent, du fait de ces marées, la distance de la Lune et la rotation terrestre.

Pour simplifier, nous supposerons tout d’abord que le plan de l’orbite lunaire coïncide avec celui de l’équateur terrestre et que cette orbite est circulaire. Il est bien clair que, par raison de symétrie, l’orbite restera alors indéfiniment dans le plan équatorial. Mais restera-t-elle toujours circulaire ? Montrons qu’il en sera bien ainsi et que, si l’excentricité est initialement nulle, elle le restera toujours. Soient $\mathrm {F}$ la force perturbatrice perpendiculaire au rayon vecteur^[3] et $ds$ le chemin parcouru par la Lune pendant le temps $dt$ : le travail de la force perturbatrice est

$d\mathrm {T} =\mathrm {F} \,ds\,\cos \alpha .$

où $\alpha$ désigne l’angle de $\mathrm {F}$ avec $ds$. Soit ${\mathcal {M}}$ le moment de rotation ; sa dérivée ${\frac {d{\mathcal {M}}}{dt}}$ est égale au moment de la force perturbatrice ; on a donc l’égalité

${\frac {d{\mathcal {M}}}{dt}}=\mathrm {F} \,r\,\cos \beta ,$

où $r$ désigne le rayon vecteur et $\beta$ l’angle de $\mathrm {F}$ avec la perpendiculaire à ce rayon vecteur.

Dans le cas d’une orbite circulaire, $\cos \alpha$ et $\cos \beta$ sont tous deux égaux à 1, et l’on a

$ds=rn\,dt,$

$n$ étant le moyen mouvement. Nous tirons alors des formules précédentes

(1)

$d\mathrm {T} =n\,d{\mathcal {M}}.$

Or, $d\mathrm {T}$ est la différentielle de la constante des forces vives $\left(-{\frac {\mathrm {M} }{2a}}\right)\,:$

$d\mathrm {T} =d\left(-{\frac {\mathrm {M} }{2a}}\right)={\frac {\mathrm {M} \,da}{2a^{2}}}\,;$

et le moment de rotation ${\mathcal {M}}$ a pour valeur

${\mathcal {M}}={\sqrt {\mathrm {M} a\left(1-e^{2}\right)}}\,;$

$\mathrm {M}$ désigne la masse de l’ensemble Terre-Lune, $2a$ et $e$ sont le grand axe et l’excentricité de l’orbite lunaire. L’équation (1) s’écrit donc

${\frac {\mathrm {M} \,da}{2a^{2}}}=n{\sqrt {\mathrm {M} }}{\frac {(1-e^{2})\,da-a\,d(e^{2})}{2{\sqrt {a(1-e^{2})}}}}.$

L’orbite étant supposée circulaire, nous faisons $e^{2}=0$ ; il vient

(2)

${\frac {\mathrm {M} \,da}{2a^{2}}}=n{\sqrt {\mathrm {M} }}{\frac {da}{2{\sqrt {a}}}}-n{\sqrt {\mathrm {M} }}{\frac {\sqrt {a}}{2}}\,d(e^{2}).$

Or, on a

$\mathrm {M} =n^{2}a^{3}\,;$

les termes en $da$ se détruisent donc dans l’équation (2) qui donne alors

$d(e^{2})=0.$

L’excentricité ne subit donc pas de variation : nulle au début, elle restera nulle.

On pourrait faire ici une objection. Il n’est pas étonnant, dira-t-on, que $d(e^{2})$ soit nul, et d’ailleurs cela ne prouve rien : en effet

$d(e^{2})=2e\,de,$

et, pour une orbite circulaire, $e$ est nul. Mais il est facile de reconnaître que, dans le calcul ci-dessus de $d(e^{2})$ (ou pour être plus précis, de sa partie séculaire), nous n’avons négligé que des termes en $e^{2}$. Donc $d(e^{2})$ est de l’ordre de $e^{2}$ et $de$ est de l’ordre de $e$ : il est par suite nul pour une orbite circulaire, et l’objection n’a pas de portée.

98.Considérons donc la Lune décrivant autour de la Terre une orbite circulaire dans le plan de l’équateur. Désignons par $y$ la vitesse angulaire de rotation de la Terre autour de son axe, par $\Omega$ la vitesse de révolution de la Lune autour de la Terre, et posons

$x=\Omega ^{-{\frac {1}{3}}}.$

Nous allons écrire que le moment de rotation du système est constant (principe des aires), et que l’énergie mécanique diminue par suite du frottement (principe de dégradation de l’énergie).

Soit $\mathrm {C}$ le moment d’inertie de la Terre autour de son axe. Le moment de rotation de la Terre est $\mathrm {C} y$ et sa demi-force vive est ${\frac {1}{2}}\mathrm {C} y^{2}$.

Tenons compte à présent du mouvement de révolution de la Lune et de la Terre autour de leur centre de gravité commun. Le moment de rotation dû à ce mouvement est proportionnel à $x$, car il a pour valeur

${\sqrt {\mathrm {M} a}}\,;$

il est donc proportionnel à ${\sqrt {a}}$ qui lui-même est proportionnel à $\Omega ^{-{\frac {1}{2}}},$ d’après l’équation

$a^{3}\Omega ^{2}=\mathrm {M} ,$

et la constante des forces vives $\left(-{\frac {\mathrm {M} }{2a}}\right)$ est proportionnelle à ${\frac {1}{a}}$ c’est-à-dire à ${\frac {1}{x^{2}}}$.

Nous choisirons les unités de façon à simplifier les coefficients de proportionnalité. Nous prendrons tout d’abord les unités de masse et de longueur de manière que $\mathrm {C} =1.$ Ensuite nous choisirons l’unité de temps de telle sorte que, pour $\Omega =1,$ le moment de rotation du système Terre-Lune dans sa révolution autour de son centre de gravité soit égal à $\mathrm {C}$, c’est-à-dire à 1. Alors, le moment de rotation dû au mouvement orbital est non seulement proportionnel, mais égal à $x$. D’ailleurs, l’équation du viriel (n^o 74, p. 91)

$2{\overline {\mathrm {T} }}+{\overline {\mathrm {V} }}=0,$

qui, puisque le mouvement est circulaire, s’écrit ici

$2\mathrm {T} +\mathrm {V} =0,$

nous apprend que l’énergie totale $\mathrm {T} +\mathrm {V}$ est égale à $-\mathrm {T} ,$ c’est-à-dire à la demi-force vive changée de signe. On en conclut immédiatement qu’avec les unités choisies, la constante des forces vives, proportionnelle à ${\frac {1}{x^{2}}}$ est égale à $-{\frac {1}{2x^{2}}}.$

Pour l’ensemble du système Terre-Lune, nous avons donc le moment de rotation total

$x+y,$

et l’énergie totale

${\frac {1}{2}}y^{2}-{\frac {1}{2x^{2}}}\cdot$

Le moment de rotation reste toujours constant : nous écrivons donc

(3)

$x+y=h.$

Quant à l’énergie, elle va constamment en diminuant, absorbée qu’elle est par le frottement qui la transforme en chaleur : si donc nous posons

$\mathrm {Y} =y^{2}-{\frac {1}{x^{2}}}$

$\mathrm {Y}$ ira toujours en décroissant.

Si nous remplaçons $y$ par sa valeur $h-x$ tirée de l’équation (3), $\mathrm {Y}$ devient fonction de $x$. Nous obtiendrons ses maxima et ses minima en annulant ${\frac {d\mathrm {Y} }{dx}}$ :

${\begin{alignedat}{3}{\frac {d\mathrm {Y} }{dx}}&=2y{\frac {dy}{dx}}&{}+{}&{\frac {2}{x^{3}}}\\[0.75ex]&=-2y&{}+{}&{\frac {2}{x^{3}}}\cdot \end{alignedat}}$

Annuler ${\frac {d\mathrm {Y} }{dx}}$ revient donc à écrire

$x^{3}y=1,$

ou encore, se rappelant la définition de $x$,

$y=\Omega .$

Ainsi, lorsque l’énergie ${\frac {\mathrm {Y} }{2}}$ est maximum ou minimum, la vitesse angulaire de rotation de la Terre est égale à la vitesse angulaire de révolution de la Lune.

fig.26.

99.Prenons, avec Sir G. H. Darwin, $x$ pour abscisse et $y$ pour ordonnée ; et traçons (fig. 26) la droite

(3)

$x+y=h,$

et la courbe

(4)

$x^{3}y=1.$

Cette courbe, Sir G. H. Darwin la nomme courbe de rigidité parce que si le point représentatif $(x,y)$ est sur cette courbe, la durée de rotation de la Terre égale la durée de révolution de la Lune, et l’ensemble Terre-Lune tourne d’un seul bloc à la façon d’un corps solide.

Deux cas sont à distinguer suivant la valeur de la constante $h$. Ou bien la droite (3) coupe la courbe de rigidité (4) en deux points C et D ; ou bien la droite (3) ne coupe pas la courbe (4).

Prenons d’abord le premier cas, et étudions $\mathrm {Y}$ en fonction de $x.$ Nous avons

$\mathrm {Y} =(h-x)^{2}-{\frac {1}{x^{2}}}\cdot$

Si nous prenons $x$ pour abscisse et $\mathrm {Y}$ pour ordonnée, cette équation représente une courbe telle que celle de la figure 27 : les points C′ et
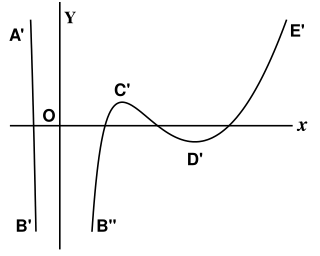
fig.27. D’ où $\mathrm {Y}$ passe par un maximum et par un minimum correspondent aux mêmes abscisses que les points C et D de la figure 26 situés sur la courbe de rigidité.

Dans le second cas, où la droite (3) ne coupe pas la courbe de rigidité (4), la fonction $\mathrm {Y}$ de $x$ ne présente plus ni maximum ni minimum, et la courbe de la figure 27 est remplacée par celle de la figure 28.

Nous pouvons maintenant suivre les changements subis par le système formé par la planète et son satellite.

Supposons que l’état initial soit représenté par un point de la droite ABCDE (fig. 26) : alors le point représentatif $(x,y)$ restera toujours sur cette droite, mais de telle façon que $\mathrm {Y}$ aille toujours en décroissant.

Si le point représentatif $(x,y)$ initial est situé entre A et B (fig. 26), le point $(x,\mathrm {Y} )$ (fig. 27) est situé sur la branche A′B′ et, puisque $\mathrm {Y}$ diminue toujours, il décrit cette branche en allant de A′ vers B′ . Le point $(x,y)$ (fig. 26) décrit donc la portion de droite AB en avançant toujours à droite, jusqu’au point B qui représente l’état final. En ce point on a $x=0,$ c’est-à-dire $\Omega =\infty \,;$ autrement dit, le satellite finira par tomber sur la planète. Remarquons que, dans ce cas, le satellite circule toujours autour de sa planète dans un sens inverse de celui de la rotation de celle-ci $(x<0,\,y>0).$
fig.28.

Nous arriverions à une conclusion analogue — le satellite tomberait finalement sur la planète — si le point représentatif $(x,y)$ initial était situé entre B et C, car alors le point $(x,\mathrm {Y} )$ (fig. 27) décrirait la branche de courbe C′B′′ en allant toujours vers B′′. Cette fois, les deux mouvements de rotation de la planète et de circulation du satellite sont de même sens $(x>0,\,y>0)$ ; mais puisqu’on a

$x^{3}y<1,$

c’est-à-dire

$y<\Omega ,$

le mouvement angulaire du satellite est plus rapide que celui de la planète : le mois est plus court que le jour.

Supposons maintenant que le point représentatif $(x,y)$ soit entre C et D (fig. 26). Les deux mouvements sont alors directs $(x>0,\,y>0),$ et le mois est plus long que le jour $(x^{3}y>1)$ : c’est le cas offert par le système Terre-Lune. Alors le point $(x,\mathrm {Y} )$ (fig. 27) décrira l’arc C′D′ en marchant vers D′ puisque $\mathrm {Y}$ décroît. L’état final est représenté par le point D de la courbe de rigidité (fig. 26), pour lequel les deux durées de rotation et de révolution sont égales.

Enfin, si le point représentatif $(x,y)$ était situé entre D et E, l’état final serait encore le point D, puisque le point $(x,\mathrm {Y} )$ (fig. 27) décrirait alors la branche E′D′. Dans ce cas, le mois est toujours plus court que le jour $(x^{3}y<1),$ le mouvement du satellite est toujours direct $(x>0),$ mais celui de la planète a pu commencer par être rétrograde $(y<0).$

Dans le cas où la droite

$x+y=h$

ne couperait pas la courbe de rigidité, la figure 27 serait remplacée par la figure 28. L’état final serait toujours le point B′ ou B′′ c’est-à-dire que le satellite finirait toujours par tomber sur la planète.

La plupart des satellites connus correspondent au cas où les deux mouvements sont de même sens, mais avec le mois plus long que le jour : le point représentatif $(x,y)$ est alors (fig. 26) entre C et D.

100.Étudions spécialement le système Terre-Lune. Pour ce système, on a les valeurs numériques suivantes

$x=3,2,\quad y=0,8,\quad h=4.$

et le point représentatif se trouve dans une position telle que P. Ce point se déplace lentement vers le point D qui représente l’état final. Si, au lieu de chercher à prévoir l’avenir, nous remontons dans le passé, nous pouvons dire que le système Terre-Lune est parti de l’état initial représenté par C. Dans cet état initial, le mois égalait le jour et leur durée commune était de 5^h,36. La durée du mois et celle du jour se sont mises ensuite à croître, la première plus vite que la seconde, en même temps que la Lune s’éloignait de la Terre. Lorsque l’état final D sera atteint, le mois sera redevenu égal au jour, leur durée commune étant d’environ 55 jours actuels. Cet état final serait définitif si la Terre et la Lune existaient seules. Mais le Soleil produit aussi sur la terre des marées qui continueront à retarder sa rotation : le jour et le mois continueront donc à croître, quoique lentement, et la Lune s’éloignera de plus en plus de la Terre, qui pourra finir par perdre son satellite.

Dans l’état initial, la durée de révolution de la Lune, 5^h,36, était courte et par suite la distance de cet astre à la Terre était faible : le calcul montre que cette distance était de 21/2 rayons terrestres. Donc, d’après les idées de Sir G. H. Darwin, la Lune aurait pris naissance tout près de la Terre, et son orbite se serait peu à peu élargie et dilatée. Nous remarquons là un contraste complet avec la théorie de Faye selon laquelle, nous l’avons vu, le satellite se formerait très loin de l’astre central, son orbite se rétrécissant peu à peu à mesure que la masse de l’astre central augmenterait par suite de la condensation.

101.Dans tout ce qui précède, nous avons regardé $\mathrm {C}$, moment d’inertie de la Terre, comme constant. Or, la Terre, en se contractant par suite du refroidissement, diminue de volume et $\mathrm {C}$ décroît. Nous étudierons un peu plus loin l’effet qui en résulte. Cependant disons dès maintenant que, pour la Terre, cet effet paraît peu important et ne change pas beaucoup l’allure générale des phénomènes.

102.Pour le système Terre-Lune, le point représentatif actuel P (fig. 26) est assez voisin du point D, puisque $x=3,2$ est sensiblement plus grand que $y=0,8.$ Par conséquent, ce système est relativement assez près de son état final.

Si nous nous occupons maintenant des systèmes formés par les autres planètes et leurs satellites, nous constatons, au contraire, que le rapport ${\frac {x}{y}}$ se trouve être extrêmement petit. Par conséquent, leur point représentatif, au lieu d’être voisin du point D, est voisin du point C. Ces systèmes sont donc beaucoup plus près de leur état initial que de leur état final. Cela tient à ce que, pour ces systèmes, la masse des satellites est extrêmement faible par rapport à la masse de la planète ; les marées sont donc peu importantes et n’ont pas encore eu le temps de produire un effet considérable.

Pour le système formé par le Soleil et l’ensemble des planètes, la masse des planètes est sans doute fort petite par rapport à celle du Soleil, mais les rayons de gyration sont très grands, et l’on constate que le rapport ${\frac {x}{y}}$ est aussi très grand. Il semble donc que ce système doive être très près de son état final. Mais cette affirmation ne supporte pas l’examen. Les planètes, en effet, produisent sur le Soleil des marées qui retardent sa rotation ; et c’est de ces marées qu’il faut tenir compte si l’on cherche les variations de la rotation du Soleil. Mais, inversement, le Soleil produit des marées sur les planètes, et ces dernières marées sont beaucoup plus fortes que les premières : leur effet devrait donc s’être produit depuis longtemps, c’est-à-dire que les planètes devraient toujours tourner une même face vers le Soleil, ce qui n’a pas lieu.

III. — Cas général.

103.Dans l’exposé qui précède, nous avons, pour simplifier, supposé nulles l’excentricité de l’orbite lunaire et l’inclinaison de cet orbite sur le plan de l’équateur terrestre. Nous allons à présent nous affranchir de ces hypothèses et entrer dans le détail de la théorie de Sir G. H. Darwin.

Auparavant, il est nécessaire de rappeler quelques points de la théorie statique des marées^[4].

Dans cette théorie statique, on suppose que la mer prend à chaque instant sa forme d’équilibre : la surface libre de l’océan est donc une surface de niveau relativement à la somme des potentiels de la gravité et de l’astre perturbateur qui produit la marée.

Le potentiel de la gravité peut se représenter par

(5)

$\mathrm {V} _{0}-g\zeta ,$

$\mathrm {V} _{0}$ désignant la valeur constante de ce potentiel au niveau moyen des mers et $\zeta$ la dénivellation de la particule liquide superficielle envisagée^[5].

Le potentiel dû à l’astre perturbateur, nous le désignons par $\mathrm {V} _{1}$. Soient $m$ la masse de l’astre perturbateur L (qui sera, par exemple, la Lune), $r$ sa distance à un point A de la surface de la mer (fig. 29), Nous avons

(6)

$\mathrm {V} _{1}={\frac {m}{r}}.$

Comme nous rapportons les points de la mer à des axes de coordonnées invariablement liés à la Terre, il faut, pour pouvoir regarder ces axes comme fixes, appliquer à chaque point A les forces apparentes dues à leur mouvement. Mais, puisqu’il ne s’agit ici que de l’équilibre, la force centrifuge composée n’intervient pas ; il ne reste que la force d’inertie dans le mouvement d’entraînement du point A
fig.29. avec les axes. La force provenant de la rotation diurne a déjà été prise en considération dans $\mathrm {V} _{0}.$ Il suffit donc, aux forces réelles, d’ajouter la force d’inertie due à la translation des axes, c’est-à-dire, puisque l’origine est au centre de la Terre, une force accélératrice $-\mathrm {J}$ égale et contraire à l’accélération $\mathrm {J}$ que l’astre perturbateur tend à imprimer à ce point.

Soient $\mathrm {J} _{x},\mathrm {J} _{y},\mathrm {J} _{z}$ les composantes rectangulaires de $\mathrm {J}$. À chaque point A, on devra appliquer une force de composantes

$-\mathrm {J} _{x},\qquad -\mathrm {J} _{y},\qquad -\mathrm {J} _{z}\,;$

comme ces composantes ne dépendent que du temps, et non des coordonnées $x,y,z$ du point A, elles peuvent être considérées comme les dérivées partielles de la fonction

(7)

$-\left(\mathrm {J} _{x}x+\mathrm {J} _{y}y+\mathrm {J} _{z}z\right)=-\mathrm {J} a\,\cos(\mathrm {J} ,a),$

en appelant $a$ le rayon moyen des mers, égal sensiblement à la distance du point A au centre T de la Terre, et en désignant par $(\mathrm {J} ,a)$ l’angle de $\mathrm {J}$ avec le rayon TA. Finalement, en écrivant que la somme des trois expressions (5), (6) et (7) est égale à une constante, nous obtiendrons l’équation de la surface libre des océans rapportée à des axes invariablement liés à la Terre :

(8)

$\mathrm {V} _{0}-g\zeta +\mathrm {V} _{1}-\mathrm {J} a\,\cos(\mathrm {J} ,a)={\text{const}}.$

Telle est l’équation qui, dans la théorie statique, donne la dénivellation $\zeta .$ Nous allons la transformer.

104.L’accélération $\mathrm {J}$ que la Lune L imprime au centre de la Terre T a pour valeur ${\frac {m}{\rho ^{2}}},$ et est dirigée suivant la droite TL $=\rho .$ Donc l’angle $(\mathrm {J} ,a)$ n’est autre que l’angle désigné par $\sigma$ sur la figure 29 (c’est la distance zénithale géocentrique de la Lune), et l’on a

$\mathrm {J} a\cos(\mathrm {J} ,a)={\frac {ma}{\rho ^{2}}}\cos \sigma .$

Comme on a

$r^{2}=a^{2}+\rho ^{2}-2a\rho \cos \sigma ,$

le potentiel $\mathrm {V} _{1}$ dû à la Lune peut s’écrire

${\begin{aligned}\mathrm {V} _{1}&={\frac {m}{\left(\rho ^{2}-2a\rho \cos \sigma \right)^{\frac {1}{2}}}}\\[0.75ex]&={\frac {m}{\rho }}\left(1-{\frac {2a}{\rho }}\cos \sigma +{\frac {a^{2}}{\rho ^{2}}}\right)^{-{\frac {1}{2}}}\\[0.75ex]&={\frac {m}{\rho }}+{\frac {am}{\rho ^{2}}}\cos \sigma +{\frac {a^{2}m}{\rho ^{3}}}{\frac {3\cos ^{2}\sigma -1}{2}},\\\end{aligned}}$

en négligeant les termes de l’ordre de ${\frac {a^{3}}{\rho ^{4}}}$. Nous écrirons

$\mathrm {V} _{1}=\mathrm {U} _{0}+\mathrm {U} _{1}+\mathrm {U} _{2},$

en posant

${\begin{aligned}\mathrm {U} _{0}&={\frac {m}{\rho }},&\mathrm {U} _{1}&={\frac {am}{\rho ^{2}}}\cos \sigma ,&\mathrm {U} _{2}&={\frac {a^{2}m}{\rho ^{3}}}{\frac {3\cos ^{2}\sigma -1}{2}}\cdot \end{aligned}}$

Par suite, nous pouvons écrire l’équation (8) ainsi

$\mathrm {V} _{0}-g\zeta +\mathrm {U} _{0}+\mathrm {U} _{2}={\text{const.}},$

$\mathrm {V} _{0}$ et $\mathrm {U} _{0}={\frac {m}{\rho }}$ étant des constantes ne dépendant pas du point A, cette équation nous donne finalement, pour la dénivellation $\zeta ,$

$\zeta ={\frac {\mathrm {U} _{2}}{g}}+{\text{const.}}={\frac {1}{g}}{\frac {a^{2}m}{\rho ^{3}}}{\frac {3\cos ^{2}\sigma -1}{2}}+{\text{const.}}$

La constante du second membre se déterminerait en écrivant que le volume total de la mer est constant, c’est-à-dire que l’intégrale

$\iint \zeta \,d\sigma ,$

étendue à tous les éléments $d\sigma$ de la surface des mers, est nulle. On reconnaît ainsi que, si la mer recouvre toute la surface de la Terre, cette constante est nulle, et l’on a alors la formule définitive de la dénivellation statique

(9)

$\zeta ={\frac {\mathrm {U} _{2}}{g}}={\frac {1}{g}}{\frac {a^{2}m}{\rho ^{3}}}{\frac {3\cos ^{2}\sigma -1}{2}},$

105.Dans la théorie statique, on ne tient pas compte de l’inertie des eaux de la mer. Dans quelle mesure cela est-il légitime ? L’inertie, proportionnelle à l’accélération, joue un rôle dans les marées à courte période ; au contraire, pour les marées à longue période, l’effet de l’accélération, c’est-à-dire de l’inertie, est négligeable. Mais que doit-on entendre par longue et courte période ? La période d’une marée pourra être qualifiée de longue ou de courte suivant que cette période sera ou ne sera pas très considérable par rapport à la période d’oscillation propre de la mer.

Par conséquent, si la période d’oscillation propre est très courte, toutes les marées, même les marées semi-diurnes, pourront être considérées comme étant à longue période, et la théorie statique s’appliquera. Or, si, avec Sir G. H. Darwin, nous considérons la Terre aux époques reculées où elle était entièrement liquide, nous trouvons que sa période propre d’oscillation est effectivement très petite par rapport à la demi-journée : il est donc, légitime de se contenter de la théorie statique.

Au contraire, l’inertie jouerait un rôle important, et la théorie statique deviendrait tout à fait insuffisante, si l’on voulait étudier le mouvement des océans actuels, dont la période propre d’oscillation est de l’ordre du demi-jour.

106.Mais si, dans le calcul de l’action des marées produites par la Lune sur la Terre, nous pouvons négliger l’inertie, nous devons en revanche tenir compte de la viscosité, puisque ce sont précisément ses effets que nous voulons étudier.

Reprenons la formule de la dénivellation statique

(9)

$\zeta ={\frac {\mathrm {U} _{2}}{g}}={\frac {1}{g}}{\frac {a^{2}m}{\rho ^{3}}}{\frac {3\cos ^{2}\sigma -1}{2}}\cdot$

Le mouvement de l’astre perturbateur L étant connu en fonction du temps $t$, le troisième membre de cette formule peut être développé sous forme trigonométrique

$\sum \mathrm {A} \cos \alpha t,$

les $\mathrm {A}$ étant des fonctions des coordonnées $x,y,z$ du lieu géographique et les $\alpha$ étant des constantes. Nous envisagerons séparément chacun des termes de la somme $\sum$ et, pour tenir compte de la viscosité, nous ajouterons au second membre de l’équation qui donne $\zeta$ un terme négatif proportionnel ${\frac {d\zeta }{dt}}.$ L’équation en $\zeta$ prend ainsi la forme

$\zeta =\mathrm {A} \cos \alpha t-k{\frac {d\zeta }{dt}},$

ou encore

(10)

$k{\frac {d\zeta }{dt}}+\zeta =\mathrm {A} \cos \alpha t,$

$k$ étant une constante proportionnelle à la viscosité du liquide.

Pour intégrer cette équation linéaire à second membre, nous considérerons l’équation suivante :

(11)

$k{\frac {d\zeta }{dt}}+\zeta =\mathrm {A} e^{i\alpha t},$

où $i$ désigne l’imaginaire ${\sqrt {-1}},$ et nous ne conserverons que la partie réelle de sa solution. Cette solution est de la forme

$\zeta =\mathrm {C} e^{i\alpha t}\,;$

en la substituant dans l’équation (11), il vient pour déterminer $\mathrm {C} ,$ l’équation

$\mathrm {C} (1+ik\alpha )=\mathrm {A} .$

Posant

(12)

$k\alpha =\operatorname {tg} \varepsilon ,$

on aura

$1+i\,k\alpha =1+i\operatorname {tg} \varepsilon ={\frac {e^{i\varepsilon }}{\cos \varepsilon }}\,;$

par suite

$\mathrm {C} =\mathrm {A} \cos \varepsilon \,e^{-i\varepsilon }.$

Et l’intégrale de l’équation (11) est

$\zeta =\mathrm {A} \cos \varepsilon \,e^{-i(\alpha t-\varepsilon )},$

dont la partie réelle

$\zeta =\mathrm {A} \cos \varepsilon \cos(\alpha t-\varepsilon )$

est l’intégrale cherchée de l’équation (10).

Nous voyons donc que l’effet de la viscosité est d’abord de réduire l’amplitude de la marée dans le rapport de $\cos \varepsilon$ à 1, ensuite d’amener pour la marée un retard de phase, un décalage, égal à $\varepsilon .$

Si l’astre sur lequel se produit la marée, au lieu d’être liquide et visqueux, était solide et parfaitement élastique, nous aurions bien une réduction de l’amplitude, mais nous n’aurions pas de décalage. S’il était solide et visqueux, nous aurions à la fois une réduction de l’amplitude plus grande que $\cos \varepsilon$ et un décalage.

107.Reprenons la formule (12) qui définit $\varepsilon$

(12)

$\operatorname {tg} \varepsilon =k\alpha .$

Si la viscosité est très faible, c’est-à-dire si $k$ est très petit, l’angle $\varepsilon$ est petit, il se confond sensiblement avec sa tangente et il est proportionnel à $\alpha ,$ c’est-à-dire à la vitesse de la marée ; de même $\sin \varepsilon$ et $\sin 2\varepsilon$ seront proportionnels à $\alpha \,;$ quant à $\cos \varepsilon$ il sera presque égal à $1$. Au contraire, si la viscosité était très forte, $k$ serait très grand, $\operatorname {tg} \varepsilon$ aussi, $\varepsilon$ serait voisin de ${\frac {\pi }{2}},$ et l’on aurait sensiblement

$\operatorname {cotg} \varepsilon ={\frac {\pi }{2}}-{\frac {1}{k\alpha }}\,;$

dans ce cas, $\sin \varepsilon$ serait très sensiblement égal à $1$ ; $\cos \varepsilon$, égal alors à $\operatorname {cotg} \varepsilon$, serait proportionnel à ${\frac {1}{\alpha }},$ et $\sin 2\varepsilon =2\sin \varepsilon \cos \varepsilon$ serait aussi proportionnel à ${\frac {1}{\alpha }}$.

Dans le cas actuel devons-nous considérer la viscosité comme faible ou comme forte ? Nous devons la considérer comme faible, car une substance comme la poix nous donnerait, si nous faisions le calcul, un angle $\varepsilon$ très petit et non voisin de ${\frac {\pi }{2}}$. La poix doit donc être considérée, au point de vue qui nous occupe, comme un corps à viscosité très faible, et il y a lieu d’admettre que la Terre, à l’époque où elle était liquide, n’offrait pas une viscosité incomparablement supérieure à celle de la poix.

108.Revenons à la formule de la dénivellation statique

(9)

$\zeta ={\frac {\mathrm {U} _{2}}{g}}={\frac {1}{g}}{\frac {a^{2}m}{\rho ^{3}}}{\frac {3\cos ^{2}\sigma -1}{2}},$

et indiquons maintenant comment on pourrait développer effectivement son troisième membre sous forme trigonométrique.

Représentons sur une sphère le pôle boréal P, le lieu géographique A et l’astre perturbateur L, de façon à former un triangle sphérique PAL (triangle Pôle-Zénith-Astre) dont les trois côtés sont

PA	$=\delta$		colatitude du lieu,
PL	$=\delta '$		complément de la déclinaison de l’astre,
LA	$=\sigma$		distance zénithale géocentrique de l’astre.

L’angle APL $={\mathcal {A}}$ est l’angle horaire de l’astre relativement au point A où on étudie la marée. La formule fondamentale de la trigonométrie sphérique, appliquée au triangle sphérique PAL, nous donne l’équation suivante :

$\cos \sigma =\cos \delta \,\cos \delta '\,+\sin \delta \,\sin \delta '\,\cos {\mathcal {A}},$

d’où nous tirons

$\cos ^{2}\!\sigma =\cos ^{2}\!\delta \cos ^{2}\!\delta '+\sin ^{2}\!\delta \sin ^{2}\!\delta '{\frac {1+\cos 2{\mathcal {A}}}{2}}+2\sin \delta \cos \delta \sin \delta '\cos \delta '\cos {\mathcal {A}}.$

Si nous portons cette valeur dans la formule (9), nous voyons que $\zeta$ contient trois sortes de termes^[6] :

1^o Des termes indépendants de l’angle horaire ${\mathcal {A}}$ : ils donneront les marées à longue période ;

2^o Des termes en $\cos 2{\mathcal {A}}$ dont la période est voisine d’un demi-jour : ils donneront les marées semi-diurnes ;

3^o Des termes en $\cos {\mathcal {A}}$ dont la période est voisine d’un jour : ils correspondent aux marées diurnes.

Introduisons les éléments osculateurs de l’orbite de l’astre L. Soient, sur la sphère céleste (fig. 30), E le plan de l’équateur terrestre, O le plan de l’orbite de l’astre troublant L, N le nœud de l’orbite sur
fig.30. l’équateur, A₀ l’origine des longitudes géographiques (intersection de l’équateur avec le méridien de Paris), A′ l’intersection de l’équateur avec le méridien du lieu géographique A, $\varpi$ le périgée de l’astre. Nous avons

A′A0	$=\chi _{0}$		longitude du lieu,
A0N	$=\chi$		angle horaire du nœud à Paris.

Nous désignons par $\varpi$ l’arc N$\varpi$ égal à la longitude du périgée moins la longitude du nœud ; et par $l$ la longitude moyenne de l’astre dans son orbite, comptée à partir du nœud N.

Alors, si nous développons le troisième membre de la formule (9), autrement dit $\cos ^{2}\sigma ,$ en série de fonctions trigonométriques dont l’argument est une fonction linéaire du temps $t$, nous obtiendrons des termes tels que

(13)

$\mathrm {M} \cos \left(\alpha \chi +\alpha \chi _{0}+\beta l+\gamma \varpi \right),$

$\mathrm {M}$ étant une fonction des coordonnées du lieu A, et $\alpha ,$ $\beta ,$ $\gamma$ étant des entiers. C’est en effet des quantités

$\chi +\chi _{0},\quad l,\quad \varpi$

que dépendent les coordonnées horaires de l’astre ${\mathcal {A}}$ et $\delta '.$

Puisque dans l’expression (13), $\chi _{0}$ ne dépend comme $\mathrm {M}$ que des coordonnées du lieu A, et non de l’astre, nous l’isolerons en développant le cosinus sous la forme

(14)

$\cos \alpha \chi _{0}\,\cos(\alpha \chi +\beta l+\gamma \varpi )-\sin \alpha \chi _{0}\,\sin(\alpha \chi +\beta l+\gamma \varpi ).$

Et finalement les différents termes du développement trigonométrique de $\zeta$ seront de la forme

(15)

$\mathrm {AX} \,\cos(\alpha \chi +\beta l+\gamma \varpi +h).$

où la constante $h$ vaut $0$ ou $\textstyle \pm {\frac {\pi }{2}}$, suivant que l’on prend le cosinus ou le sinus qui figure dans la formule (14), et où nous désignons par $\mathrm {AX}$ le coefficient qui dépend des coordonnées du lieu géographique.

De quelle nature seront ces coefficients $\mathrm {AX}$ en tant que fonctions des coordonnées du lieu ? Ils seront évidemment des fonctions sphériques du second ordre comme l’est lui-même le troisième membre de la formule (9). Nous avons désigné chacun de ces coefficients par un produit $\mathrm {AX}$ : la lettre $\mathrm {A}$ désigne une constante numérique, et la lettre $\mathrm {X}$ une fonction sphérique du second ordre multipliée par un nombre convenable de telle façon que l’intégrale

$\iint \mathrm {X} ^{2}\,d\sigma ,$

étendue à tous les éléments de surface $d\sigma$ de la sphère, ait une même valeur constante $\mathrm {K}$ pour toutes les fonctions sphériques que nous aurons à envisager.

Soient $x,y,z$ les coordonnées du lieu par rapport à trois axes rectangulaires invariablement liés à la Terre et passant par son centre, l’axe des $z$ étant l’axe de rotation, le plan des $xz$ étant le méridien de Paris. Nous aurons (en prenant pour unité le rayon terrestre $a$)

${\begin{aligned}x&=\sin \delta \,\cos \chi _{0},\\y&=\sin \delta \,\sin \chi _{0},\\z&=\cos \delta .\end{aligned}}$

Les fonctions sphériques $\mathrm {X}$ qu’introduit alors le développement trigonométrique du troisième membre de la formule (9) sont les suivantes^[7] :

${\begin{aligned}{\frac {x^{2}-y^{2}}{2}}&={\frac {\sin ^{2}\delta }{2}}\,\cos 2\chi _{0},\\[0.5ex]xy&={\frac {\sin ^{2}\delta }{2}}\,\sin 2\chi _{0},\\[0.5ex]xz&=\sin \delta \,\cos \delta \,\cos \chi _{0},\\[0.5ex]yz&=\sin \delta \,\cos \delta \,\sin \chi _{0},\\[0.5ex]{\frac {x^{2}+y^{2}-2z^{2}}{2{\sqrt {3}}}}&={\frac {1-3\cos ^{2}\delta }{2{\sqrt {3}}}}\cdot \end{aligned}}$

Faisons maintenant quelques remarques sur les trois entiers $\alpha ,$ $\beta ,$ $\gamma .$ Tout d’abord on aura

$\alpha ={}$0, 1 ou 2,

suivant que le terme considéré correspond à une marée à longue période, à une marée diurne, ou à une marée semi-diurne ; car, dans l’expression (15), $\beta l$ et $\gamma \varpi$ ne varient que très lentement et peuvent être regardés comme sensiblement constants. Ensuite, si l’inclinaison est nulle, on aura

$\alpha +\beta +\gamma =0,$

car alors les deux plans E et O (fig. 30) coïncident, le point N devient indéterminé, et les seuls angles qui interviennent sont $\chi -\varpi$ et $\chi -l$. Par suite, dans les termes indépendants de l’inclinaison, on aura

$\alpha +\beta +\gamma =0.$

Dans les termes qui contiennent l’inclinaison à la puissance $\lambda$, on verrait facilement que

$|\alpha +\beta +\gamma |$

doit être au plus égal à $\lambda$ et de même parité que $\lambda$. Enfin, dans les termes indépendants de l’excentricité, $\varpi$ n’intervient pas, on a donc

$\gamma =0\,;$

et dans les termes qui contiennent l’excentricité à la puissance $\lambda ,$ on verrait que $|\gamma |$ est au plus égal à $\lambda$ et de même parité que $\lambda$.

Comme nous ne conserverons dans la suite que des termes du premier ordre au plus par rapport à l’excentricité $e$ et à l’inclinaison $i$, nous aurons, dans les termes indépendants de $e$ et de $i,$

${\begin{aligned}\gamma &=0,&\alpha +\beta &=0\,;\end{aligned}}$

dans les termes en $e$,

${\begin{aligned}\gamma &=\pm 1,&\,\alpha +\beta +\gamma &=0\,;\end{aligned}}$

dans les termes en $i$,

${\begin{aligned}\gamma &=0,&\,\alpha +\beta &=\pm 1.\end{aligned}}$

109.Bref, nous avons prouvé que le troisième membre de la formule (9), qui représente (au facteur $g$ près) le potentiel $\mathrm {U} _{2}$ générateur de la marée, peut se développer en une série de termes de la forme (15) :

${\frac {\mathrm {U} _{2}}{g}}=\sum \mathrm {AX} \,\cos(\alpha \chi +\beta l+\gamma \varpi +h),$

ce que nous écrivons simplement

${\frac {\mathrm {U} _{2}}{g}}=\sum \mathrm {AX} \,\cos \theta ,$

en posant pour abréger

$\theta =\alpha \chi +\beta l+\gamma \varpi +h.$

Si nous voulons maintenant tenir compte de la viscosité comme nous l’avons fait au n^o 106 (p. 146), nous trouverons que ce potentiel perturbateur $\mathrm {U} _{2}$ produit une dénivellation

(16)

$\zeta =\sum \mathrm {AX} \,\cos \varepsilon \,\cos(\theta -\varepsilon ),$

où $\varepsilon$ est donné par la formule

$\operatorname {tg} \varepsilon =k{\frac {d\theta }{dt}},$

$\left({\frac {d\theta }{dt}}\right.$ représente ici la vitesse de la marée que nous appelions $\alpha$ au n^o 106)^[8].

Nous nous proposons de chercher l’action de la Terre, ainsi déformée par la marée (16), sur un corps extérieur. Pour fixer les idées, nous supposerons que la marée (16) est produite par le Soleil et nous chercherons les perturbations que cette marée solaire (16) fait subir au mouvement de la Lune.

Les quantités $\chi ,l,\varpi$ sont donc relatives au Soleil. Nous appellerons $\chi ',l',\varpi '$ les mêmes quantités relatives à la Lune. Comme nous cherchons l’action, sur l’orbite de la Lune, du bourrelet soulevé par la marée solaire à la surface de la Terre, nous introduirons une fonction perturbatrice $\mathrm {W}$ qui sera le potentiel dû à l’attraction de ce bourrelet.
fig.31. Soit $r'$ la distance de la Lune L à l’élément $\zeta \,d\sigma$ du bourrelet (fig. 31). Nous aurons alors

$\mathrm {W} =\iiint {\frac {\zeta \,d\sigma }{r'}},$

l’intégrale étant étendue à toute la surface de la sphère terrestre.

Nous pouvons développer ${\frac {1}{r'}}$ comme nous avons développé ${\frac {1}{r}}$ au n^o 104 (p. 144) et écrire

${\frac {1}{r'}}=\mathrm {U} '_{0}+\mathrm {U} '_{1}+\mathrm {U} '_{2},$

$\mathrm {U} '_{0},\,\mathrm {U} '_{1},\,\mathrm {U} '_{2},$ étant respectivement des fonctions sphériques d’ordre 0, 1, 2, par rapport aux coordonnées du lieu géographique A. Comme $\zeta$ est lui-même une fonction sphérique du second ordre par rapport aux coordonnées du même point A, on a

${\begin{aligned}\iint \zeta \mathrm {U} '_{0}\,d\sigma &=0,&\iint \zeta \mathrm {U} '_{1}\,d\sigma &=0.\end{aligned}}$

Nous avons donc simplement pour notre fonction perturbatrice

(17)

$\mathrm {W} =\iint \zeta \mathrm {U} '_{2}\,d\sigma .$

Développons $\mathrm {U} '_{2}$ sous forme trigonométrique de la même manière que nous avons développé $\mathrm {U} _{2}$ un peu plus haut : nous aurons

$\mathrm {U} '_{2}=\sum \mathrm {A} '\mathrm {X} '\,\cos(\alpha '\chi '+\beta 'l'+\gamma '\varpi '+h'),$

$\alpha ',\,\beta ',\,\gamma '$ étant trois entiers, $h'$ étant une constante égale à 0 ou à $\textstyle \pm {\frac {\pi }{2}},$ $\mathrm {A} '$ étant un coefficient numérique, et $\mathrm {X} '$ une fonction sphérique du second ordre telle que l’intégrale

$\iint \mathrm {X} '^{2}\,d\sigma$

étendue à toute la sphère ait une valeur constante donnée $\mathrm {K} ,$ la même pour toutes les fonctions sphériques $\mathrm {X} '.$ Nous écrirons simplement

(18)

$\mathrm {U} '_{2}=\sum \mathrm {A} '\mathrm {X} '\,\cos \theta ',$

en désignant, pour abréger, par

$\theta '=\alpha '\chi '+\beta 'l'+\gamma '\varpi '+h'$

l’argument du cosinus. Alors, d’après (16) et (18), l’expression (17) de $\mathrm {W}$ peut s’écrire, en faisant sortir du signe $\iint$ tout ce qui ne dépend pas des coordonnées du lieu A,

(19)

$\mathrm {W} =\sum \mathrm {AA} '\,\cos \varepsilon \,\cos(\theta -\varepsilon )\,\cos \theta '\,\iint \mathrm {XX} '\,d\sigma .$

Telle est l’expression de la fonction perturbatrice dont nous avons à chercher l’action sur l’orbite de la Lune.

110.Nous appliquerons la méthode de la variation des constantes. Nous commencerons par définir la position de la Lune par un système de six éléments canoniques^[9]. Aux trois quantités $\chi ',$ $\varpi ',$ $l',$ nous adjoindrons, pour achever de déterminer la position de la Lune, les trois suivantes :

${\begin{aligned}\xi '&={\sqrt {a'}},\\[0.75ex]\eta '&=1-{\sqrt {1-e'^{2}}},\\[0.75ex]\mu '&=2\sin ^{2}{\frac {i'}{2}}=1-\cos i',\end{aligned}}$

$a',\,e',\,i'$ représentant le demi-grand axe, l’excentricité et l’inclinaison sur l’équateur de l’orbite lunaire.

Le vecteur des aires a alors pour valeur (à un facteur constant près dépendant des masses et dont nous faisons abstraction)

${\sqrt {a'}}{\sqrt {1-e'^{2}}}=\xi '(1-\eta '),$

et la projection de ce vecteur sur la perpendiculaire au plan de l’équateur a pour valeur

${\sqrt {a'}}{\sqrt {1-e'^{2}}}\cos i'=\xi '(1-\eta ')(1-\mu ').$

Les six éléments

$\xi ',\quad \xi '(1-\eta '),\quad \xi '(1-\eta ')(1-\mu '),\quad l'-\varpi ',\quad \varpi ',\quad -\chi ',$

forment un système de variables canoniques^[10] entre lesquelles existent les équations de Hamilton. Nous aurons en particulier

(20)

$\left\{{\begin{aligned}{\frac {d\xi '}{dt}}&={\frac {d\mathrm {W} }{d(l'-\varpi ')}},\\[0.75ex]{\frac {d[\xi '(1-\eta ')]}{dt}}&={\frac {d\mathrm {W} }{d\varpi '}},\\[0.75ex]{\frac {d[\xi '(1-\eta ')(1-\mu ')]}{dt}}&={\frac {d\mathrm {W} }{d(-\chi ')}}.\end{aligned}}\right.$

Telles sont les équations auxquelles nous conduit l’application de la méthode de la variation des constantes, pour calculer les perturbations des éléments lunaires sous l’action de la fonction perturbatrice $\mathrm {W} .$

111.Le calcul qui précède est relatif à l’action, sur l’orbite lunaire, du bourrelet liquide soulevé sur les océans terrestres par la marée solaire. Ne pourrait-on pas appliquer le même calcul à l’action, sur l’orbite lunaire, du bourrelet liquide soulevé par la marée lunaire elle-même ? On le peut certainement, mais à condition de prendre quelques précautions : $\chi ',$ $\varpi ',$ $l'$ devenant alors égaux à $\chi ,$ $\varpi ,$ $l$, la fonction perturbatrice $\mathrm {W}$ se trouve dépendre de la variable $\chi$ de deux manières différentes ; elle en dépend par $\chi$ et ensuite par $\chi '$. Dans le calcul de ${\frac {d\mathrm {W} }{d\chi '}},$ il faut donc supposer d’abord $\chi '\neq \chi ,$ puis dériver $\mathrm {W}$ par rapport à $\chi ',$ et enfin faire $\chi =\chi '.$ Les mêmes précautions doivent être prises dans le calcul des autres dérivées de $\mathrm {W} .$ En d’autres termes, il faut distinguer la Lune en tant qu’astre troublant producteur des marées et en tant qu’astre troublé par ces marées. C’est ainsi que Sir G. H. Darwin appelle notre satellite Diane quand il est troublant et Lune quand il est troublé : alors $\chi ,$ $\varpi ,$ $l$ sont les coordonnées de Diane, $\chi ',$ $\varpi ',$ $l'$, sont les coordonnées de la Lune, et l’on a

$\chi '=\chi ,\quad \varpi '=\varpi ,\quad l'=l.$

Moyennant cette précaution, notre analyse s’applique à l’action des marées lunaires sur la Lune elle-même,

112.Nous reprendrons donc les formules (20), et comme nous ne nous occupons que des effets séculaires, nous ne conserverons aux seconds membres que les termes constants indépendants du temps $t.$ Nous avons d’après la formule (19)

(20bis)

$\left\{{\begin{aligned}{\frac {d\mathrm {W} }{d(l'\!-\!\varpi ')}}&=-\!\!\sum \mathrm {AA} '\cos \varepsilon \cos(\theta \!-\!\varepsilon )\beta '\sin \theta '\!\iint \!\mathrm {XX} '\,d\sigma ,\\[0.75ex]{\frac {d\mathrm {W} }{d\varpi '}}&=-\!\!\sum \mathrm {AA} '\cos \varepsilon \cos(\theta \!-\!\varepsilon )(\gamma '\!+\!\beta ')\sin \theta '\!\iint \!\mathrm {XX} '\,d\sigma ,\\[0.75ex]{\frac {d\mathrm {W} }{d(-\chi ')}}&=-\!\!\sum \mathrm {AA} '\cos \varepsilon \cos(\theta \!-\!\varepsilon )\alpha '\sin \theta '\!\iint \!\mathrm {XX} '\,d\sigma .\end{aligned}}\right.$

Dans ces expressions, le temps ne figure que dans le produit

$\cos(\theta -\varepsilon )\,\sin \theta ',$

produit qui, développé, fournit des termes en

${\cos \atop \sin }(\theta -\theta '),$

et des termes en

${\cos \atop \sin }(\theta +\theta ').$

Nous aurons donc, aux seconds membres des expressions (20), un terme indépendant de $t$ chaque fois que $\theta -\theta '$ ou $\theta +\theta '$ se réduira à une constante. Comme $\theta +\theta '$ n’est jamais une constante, les termes séculaires correspondent à

$\theta -\theta '={\text{const.}}$

c’est-à-dire à

(21)

${\frac {d\theta }{dt}}={\frac {d\theta '}{dt}},$

Si l’astre troublant et l’astre troublé sont différents, cette condition n’est jamais remplie^[11], car le rapport des moyens mouvements de ces deux astres n’est pas commensurable. Nous pouvons donc dire que la marée solaire ne produit pas d’effet séculaire sur l’orbite lunaire.

Mais si l’astre troublant et l’astre troublé sont identiques, la condition (21) est remplie chaque fois que $\theta =\theta '$ et n’est remplie que dans ce cas : on a alors

$\cos(\theta -\varepsilon )\sin \theta '={\frac {1}{2}}\sin(\theta '-\theta +\varepsilon )+{\frac {1}{2}}\sin(\theta '+\theta -\varepsilon ),$

qui donne le terme constant

${\frac {1}{2}}\sin(\theta '-\theta +\varepsilon )={\frac {1}{2}}\sin \varepsilon .$

Les seconds membres des formules (20^bis), dans lesquels on ne conserve que les termes constants indépendants de $t$, deviennent donc

${\begin{aligned}-\sum \mathrm {AA} '{\frac {\sin 2\varepsilon }{4}}&\beta '\iint \mathrm {XX} '\,d\sigma ,\\[0.5ex]-\sum \mathrm {AA} '{\frac {\sin 2\varepsilon }{4}}&(\gamma '+\beta ')\iint \mathrm {XX} '\,d\sigma ,\\[0.5ex]\sum \mathrm {AA} '{\frac {\sin 2\varepsilon }{4}}&\alpha '\iint \mathrm {XX} '\,d\sigma ,\end{aligned}}$

Nous pouvons maintenant effacer les accents « prime » devenus inutiles, puisque tout se rapporte au même astre, la Lune. Nous remarquons que le facteur

$-{\frac {1}{4}}\iint \mathrm {X} ^{2}\,d\sigma$

est le même pour tous les termes, puisque nous avons eu soin de choisir les fonctions sphériques $\mathrm {X}$ de façon que cette intégrale ait toujours la même valeur constante $\mathrm {K}$ (note de la p. 151). Nous n’écrivons donc pas ce facteur, qui est le même partout (quitte à le rétablir plus tard), et les formules (20^bis) prennent la forme

(20ter)

$\left\{{\begin{alignedat}{2}{\frac {d\mathrm {W} }{d(l-\varpi )}}&={}&&\sum \mathrm {A} ^{2}\beta \sin 2\varepsilon ,\\[0.5ex]{\frac {d\mathrm {W} }{d\varpi }}&={}&&\sum \mathrm {A} ^{2}(\gamma +\beta )\sin 2\varepsilon ,\\[0.5ex]{\frac {d\mathrm {W} }{d(-\chi )}}&={}&-&\sum \mathrm {A} ^{2}\alpha \sin 2\varepsilon .\end{alignedat}}\right.$

Rappelons-nous que l’angle $\varepsilon$ est très petit et que par suite $\sin 2\varepsilon$ est proportionnel à $\operatorname {tang} \varepsilon$, c’est-à-dire à la vitesse de la marée ${\frac {d\theta }{dt}}$. Or,

${\frac {d\theta }{dt}}=\alpha {\frac {d\chi }{dt}}+\beta {\frac {dl}{dt}}+\gamma {\frac {d\varpi }{dt}},$

et l’on a

$\,{\frac {d\chi }{dt}}=n$		vitesse angulaire de rotation de la Terre.
$\,{\frac {dl}{dt}}\;=\Omega$		vitesse angulaire de rotation de la Lune.
${\frac {d\varpi }{dt}}=0$		à très peu près.

Par suite, dans les formules (20^ter), nous pouvons remplacer $\sin 2\varepsilon$ par

$\alpha n+\beta \Omega$

qui lui est proportionnel.

Finalement les formules (20), dans lesquelles on ne conserve que ce qui est relatif aux termes séculaires, sont devenues

(21)

$\left\{{\begin{alignedat}{2}{\frac {d\xi }{dt}}&=&&\sum \mathrm {A} ^{2}\beta (\alpha n+\beta \Omega ),\\{\frac {d[\xi (1-\eta )]}{dt}}&=&&\sum \mathrm {A} ^{2}(\gamma +\beta )(\alpha n+\beta \Omega ),\\{\frac {d[\xi (1-\eta )(1-\mu )]}{dt}}&={}&-&\sum \mathrm {A} ^{2}\alpha (\alpha n+\beta \Omega ).\end{alignedat}}\right.$

Ces dernières formules, par un calcul immédiat, nous fournissent les suivantes :

(22)

$\left\{{\begin{alignedat}{2}{\frac {d\xi }{dt}}&=&&\sum \mathrm {A} ^{2}\beta (\alpha n+\beta \Omega ),\\\xi {\frac {d\eta }{dt}}&=&-&\sum \mathrm {A} ^{2}(\gamma +\eta \beta )(\alpha n+\beta \Omega ),\\\xi {\frac {d\mu }{dt}}&=&&\sum \mathrm {A} ^{2}(\alpha +\beta -\mu \beta )(\alpha n+\beta \Omega )+{\text{termes en}}\;\eta .\end{alignedat}}\right.$

Ces trois formules vont nous permettre de calculer les variations séculaires du grand axe, de l’excentricité et de l’inclinaison de l’orbite lunaire, provoquées par le bourrelet liquide de la marée lunaire elle-même. Dans la troisième de ces formules (22), qui nous servira à calculer la variation de l’inclinaison $(\mu =1-\cos i),$ nous négligerons les termes en $\eta$ car

$\eta =1-{\sqrt {1-e^{2}}}$

s’annule avec l’excentricité, et, dans le calcul relatif à l’inclinaison, nous pouvons, en première approximation, supposer l’excentricité nulle.

113.Les seconds membres de (22) sont des sommes de termes dont chacun provient d’un des termes

(15)

$\mathrm {AX} \,\cos(\alpha \chi +\beta l+\gamma \varpi +h)=\mathrm {AX} \,\cos \theta$

en lesquels on a pu décomposer le potentiel $\mathrm {U} _{2}$ producteur de la marée lunaire. Parmi ces termes, nous ne conserverons ici que ceux qui sont du premier ordre au plus par rapport à l’excentricité $e$ et à l’inclinaison $i$. La théorie des marées^[12] nous enseigne que ces termes sont les suivants :

Termes semi-diurnes :
$(\mathrm {M} _{2})$	$=$	$\;\;{\frac {\sin ^{2}\delta }{2}}\cos(2\chi +2\chi _{0}-2l)$	(principal semi-diurne),
$(\mathrm {N} )$	$=$	$\;\;{\frac {7e}{2}}{\frac {\sin ^{2}\delta }{2}}\cos(2\chi +2\chi _{0}-3l+\varpi )\quad$	(elliptique majeur),
$(\mathrm {L} )$	$=$	$-{\frac {e}{2}}{\frac {\sin ^{2}\delta }{2}}\cos(2\chi +2\chi _{0}-l-\varpi )$	(elliptique mineur)
Termes diurnes :
$(\mathrm {O} )$	$=$	$\sin {\frac {i}{2}}\,\sin 2\delta$ $\cos \left(\chi +\chi _{0}-2l+{\frac {\pi }{2}}\right)$	(principal diurne),
$(\mathrm {K} _{1})$	$=$	$\sin {\frac {i}{2}}\,\sin 2\delta \cos \left(\chi +\chi _{0}-{\frac {\pi }{2}}\right)$	(sidéral) ;
Terme à longue période :
$(\mathrm {M} _{m})$	$=$	${\frac {e}{2}}(1-3\cos ^{2}\delta )\cos(l-\varpi )$	(elliptique mensuel),

Ces six termes sont ceux que nous conserverons dans $\mathrm {U} _{2}$, (seul le premier $(\mathrm {M} _{2})$ est indépendant de $e$ et de $i$),

114.Tels qu’ils sont, ces six termes ne sont pas tout à fait de la forme (15) (puisque $\chi _{0}$ figure dans l’argument) ; or, il convient de les rendre de cette forme.

1^o Les trois termes semi-diurnes sont de la forme

(sd)

$\mathrm {B} {\frac {\sin ^{2}\delta }{2}}\cos(2\chi _{0}+\theta ),$

qui peut s écrire

$\mathrm {B} {\frac {\sin ^{2}\delta }{2}}\cos(2\chi _{0})\cos \theta -\mathrm {B} {\frac {\sin ^{2}\delta }{2}}\sin(2\chi _{0})\cos \left(\theta -{\frac {\pi }{2}}\right)\,;$

or,

${\frac {\sin ^{2}\delta }{2}}\,\cos 2\chi _{0}={\frac {x^{2}-y^{2}}{2}}$

et

${\frac {\sin ^{2}\delta }{2}}\,\sin 2\chi _{0}=xy$

sont justement des fonctions sphériques $\mathrm {X}$ qui donnent à l’intégrale

$\iint \mathrm {X} ^{2}\,d\sigma$

la valeur $\mathrm {K}$ (note de la p. 151). Donc chaque terme semi-diurne (sd) fournit deux termes de la forme (15) ayant respectivement pour coefficient $\mathrm {B}$ et $-\mathrm {B}$, et pour argument $\theta$ et $\theta -{\frac {\pi }{2}}$. Par suite, chaque terme semi-diurne fournit aux seconds membres des formules (22) deux termes égaux, pour lesquels on a

$\mathrm {A} ^{2}=\mathrm {B} ^{2}.$

2^o Les deux termes diurnes sont de la forme

(d)

$\mathrm {B} \,\sin 2\delta \,\cos(\chi _{0}+\theta ),$

ce qui peut s’écrire

$2\mathrm {B} \,{\frac {\sin 2\delta }{2}}\,\cos \chi _{0}\,\cos \theta -2\mathrm {B} \,{\frac {\sin 2\delta }{2}}\,\sin \chi _{0}\,\cos \left(\theta -{\frac {\pi }{2}}\right)\,;$

or,

${\frac {\sin 2\delta }{2}}\,\cos \chi _{0}=xz$

et

${\frac {\sin 2\delta }{2}}\,\sin \chi _{0}=yz$

sont justement des fonctions sphériques $\mathrm {X}$ qui donnent à l’intégrale

$\iint \mathrm {X} ^{2}\,d\sigma$

la valeur $\mathrm {K}$. Donc chaque terme diurne (d) fournit deux termes de la forme (15) ayant respectivement pour coefficient $2\mathrm {B}$ et $-2\mathrm {B}$, et pour argument $\theta$ et $\theta -{\frac {\pi }{2}}$. Par suite, chaque terme diurne fournit aux seconds membres des formules (22) deux termes égaux, pour lesquels on a

$\mathrm {A} ^{2}=4\mathrm {B} ^{2}\,;$

3^o Le terme à longue période est de la forme

$\mathrm {B} \,{\frac {1-3\cos ^{2}\delta }{2}}\,\cos \theta \,;$

et, comme

${\frac {1-3\cos ^{2}\delta }{2{\sqrt {3}}}}={\frac {x^{2}+y^{2}-2z^{2}}{2{\sqrt {3}}}}$

est une fonction sphérique $\mathrm {X}$ donnant à l’intégrale

$\iint \mathrm {X} ^{2}\,d\sigma$

la valeur $\mathrm {K}$, ce terme est de la forme (15), ayant pour coefficient $\mathrm {B} {\sqrt {3}}$. Il donnera donc aux seconds membres des formules (22) un seul terme pour lequel on aura

$\mathrm {A} ^{2}=3\mathrm {B} ^{2}.$

Comme chaque terme diurne ou semi-diurne en fournit deux égaux dans les seconds membres des formules (22), tandis que le terme longue période n’en fournit qu’un seul, il y a lieu de multiplier par 2 la quantité $\mathrm {A} '$ relative à chaque terme diurne ou semi-diurne. Au lieu de cela, nous diviserons par 2 la quantité $\mathrm {A} ^{2}$ relative au terme à longue période^[13], pour lequel on devra prendre, par conséquent,

$\mathrm {A} ^{2}={\frac {3\mathrm {B} ^{2}}{2}}.$

115.Bref, si nous prenons les six termes

$(\mathrm {M} _{2}),\quad (\mathrm {N} ),\quad (\mathrm {L} ),\quad (\mathrm {O} ),\quad (\mathrm {K} _{1}),\quad (\mathrm {M} _{m}),$

nous pouvons former le tableau suivant à double entrée :

${\begin{array}{l|c|r|r|c|c|r|c}{\begin{array}{c}\;\\[2ex]\;\end{array}}&\alpha &\beta &\gamma &\mathrm {A} ^{2}&\alpha n+\beta \Omega &-\gamma -\eta \beta &\alpha +\beta -\mu \beta \\\hline {\begin{array}{c}\;\\[2ex]\;\end{array}}\!\!\!\!{\text{Terme}}\;(\mathrm {M} _{2})&2&-2&0&1&2n-2\Omega &2\eta \quad &2\mu \\\hline {\begin{array}{c}\;\\[2ex]\;\end{array}}\!\!\!\!{\text{Terme}}\;(\mathrm {N} )&2&-3&1&{\dfrac {49}{2}}\eta &2n-3\Omega &-1\quad &\;\;{\text{»}}\\\hline {\begin{array}{c}\;\\[2ex]\;\end{array}}\!\!\!\!{\text{Terme}}\;(\mathrm {L} )&2&-1&-1&\;{\dfrac {1}{2}}\eta &2n-\;\Omega &1\quad &\;\;{\text{»}}\\\hline {\begin{array}{c}\;\\[2ex]\;\end{array}}\!\!\!\!{\text{Terme}}\;(\mathrm {O} )&1&-2&0&2\mu &\;\;n-2\Omega &{\text{»}}\quad &-1\\\hline {\begin{array}{c}\;\\[2ex]\;\end{array}}\!\!\!\!{\text{Terme}}\;(\mathrm {K} _{1})&1&0&0&2\mu &n&{\text{»}}\quad &\;\;\,1\\\hline {\begin{array}{c}\;\\[2ex]\;\end{array}}\!\!\!\!{\text{Terme}}\;(\mathrm {M} _{m})&0&1&-1&3\eta &\Omega &1\quad &\;\;{\text{»}}\\\end{array}}$

Pour le calcul des quantités $\mathrm {A} ^{2}$, $e^{2}$ a été remplacé par $2\eta$ et $\sin ^{2}{\frac {i}{2}}$ par ${\frac {\mu }{2}}$. Dans les deux dernières colonnes on n’a conservé les termes en $\eta$ et en $\mu$ que pour le terme principal ($\mathrm {M} _{2}$). Enfin, dans l’avant dernière colonne, on ne s’est pas occupé des termes $(\mathrm {O} )$ et $(\mathrm {K} _{1})$ qui contiennent $\sin {\frac {i}{2}}$ en facteur ; dans la dernière colonne, on ne s’est pas occupé des termes $(\mathrm {N} ),$ $(\mathrm {L} )$ et $(\mathrm {M} _{m})$ qui contiennent $e$ en facteur ; car, pour le calcul des variations de l’excentricité, nous supposons l’inclinaison nulle et, pour le calcul des variations de l’inclinaison, nous supposons l’excentricité nulle.

116.Le Tableau précédent fournit tous les éléments nécessaires pour calculer

${\frac {d\xi }{dt}},\qquad \xi \,{\frac {d\eta }{dt}},\qquad \xi \,{\frac {d\mu }{dt}}$

au moyen des formules (22). Nous trouvons ainsi

${\begin{aligned}{\frac {d\xi }{dt}}&=(-4n+4\Omega )+{\text{termes en}}\;\eta \;{\text{et en}}\;\mu ,\\[0.5ex]\xi \,{\frac {d\eta }{dt}}&=2\eta (2n-2\Omega )-{\frac {49}{2}}\eta (2n-3\Omega )+{\frac {1}{2}}\eta (2n-\Omega )+3\eta \Omega ,\\[0.5ex]\xi \,{\frac {d\mu }{dt}}&=2\mu (2n-2\Omega )-2\mu (n-2\Omega )+2\mu n.\end{aligned}}$

Ces trois formules s’écrivent (en négligeant au second membre de la première les termes en $\eta$ et $\mu$ à côté du premier terme qui est fini)

(23)

$\left\{{\begin{aligned}{\frac {d\xi }{dt}}&=-4n+4\Omega ,\\{\frac {1}{\eta }}\xi {\frac {d\eta }{dt}}&=-44n+72\Omega ,\\{\frac {1}{\mu }}\xi {\frac {d\mu }{dt}}&=4n.\\\end{aligned}}\right.$

Rappelons-nous que nous avons fait abstraction, aux seconds membres des formules (20) ou (22), d’un même facteur constant. Ce facteur, il est facile de le voir, est négatif. Désignons-le par $-{\frac {k}{4}}$ et rétablissons-le maintenant dans les formules (23) qui deviennent ainsi

(24)

$\left\{{\begin{aligned}{\frac {d\xi }{dt}}&=k(n-\Omega ),\\{\frac {1}{\eta }}\xi {\frac {d\eta }{dt}}&=k(11n-18\Omega ),\\{\frac {1}{\mu }}\xi {\frac {d\mu }{dt}}&=-kn.\\\end{aligned}}\right.$

Au lieu de conserver les variables $\eta$ et $\mu$, introduisons l’excentricité $e$ et l’inclinaison $i$ : nous avons, à des termes près d’ordre supérieur,

${\begin{aligned}\eta &={\frac {e^{2}}{2}},&\mu &=2\sin ^{2}{\frac {i}{2}}={\frac {i^{2}}{2}},\end{aligned}}$

et par suite

${\begin{aligned}{\frac {1}{\eta }}{\frac {d\eta }{dt}}&={\frac {2}{e}}{\frac {de}{dt}},\\{\frac {1}{\mu }}{\frac {d\mu }{dt}}&={\frac {2}{i}}{\frac {di}{dt}}.\end{aligned}}$

Les équations (24) s’écrivent donc

(25)

$\left\{{\begin{aligned}{\frac {d\xi }{dt}}&=k(n-\Omega ),\\\xi {\frac {de}{dt}}&={\frac {ke}{2}}(11n-18\Omega ),\\\xi {\frac {di}{dt}}&=-{\frac {ki}{2}}n.\\\end{aligned}}\right.$

Ces dernières équations donneront les variations du grand axe, de l’excentricité et de l’inclinaison de l’orbite lunaire par suite de l’effet des marées.

117.Nous voulons aussi calculer la variation de la vitesse angulaire $n$ de rotation de la Terre. Nous nous servirons pour cela du théorème des aires. Dans la Section 'II' de ce Chapitre, nous avons posé

$x=\Omega ^{-{\frac {1}{3}}},\qquad y=n\,;$

et l’équation des aires nous a donné (n^o 98)

(3)

$x+y=h.$

En vertu de la troisième loi de Képler, $x$ est proportionnel à la racine carrée du grand axe, c’est-à-dire à ce que nous appelons ici $\xi .$ Donc, en adoptant des unités convenables, cette équation (3) peut s’écrire

$\xi +n=h.$

Mais cette équation n’a été établie qu’en supposant nulle l’inclinaison de l’orbite lunaire sur l’équateur, hypothèse que nous abandonnons ici. Représentons (fig. 32) par O le plan de l’orbite lunaire,
fig.32. par E celui de l’équateur terrestre, et par Π le plan invariable (plan du maximum des aires).

Modifiant un peu les notations précédentes, nous appellerons $i$ l’inclinaison de l’orbite sur le plan invariable et $j$ l’inclinaison de celui-ci sur l’équateur.

Le théorème des aires donne alors les deux équations suivantes :

${\begin{aligned}\xi \cos i+n\cos j&=h,\\[0.5ex]\xi \sin i-n\sin j&=0.\end{aligned}}$

Les angles $i$ et $j$ étant supposés petits, ces équations s’écrivent approximativement

(26)

$\left\{{\begin{aligned}\xi +n&=h,\\[0.5ex]jn&=i\xi .\end{aligned}}\right.$

Ces équations nous serviront à calculer les variations des éléments terrestres $n$ et $j,$ puisque les variations des éléments lunaires $\xi$ et $i$ sont données par les équations (25). Nous aurons d’abord

(27)

${\frac {dn}{dt}}=-{\frac {d\xi }{dt}}=-k(n-\Omega ).$

Ensuite, puisque nous appelons maintenant $j+i,$ ce qui, dans les équations (25), est désigné simplement par $i,$ nous devons, dans la troisième équation (25), remplacer $i$ par $j+i$ ($di$ n’étant pas changé) ; cette équation devient

(28)

$\xi \,{\frac {di}{dt}}=-{\frac {kn}{2}}(i+j).$

Alors la seconde équation (26) donne

$j{\frac {dn}{dt}}+n{\frac {dj}{dt}}=i{\frac {d\xi }{dt}}+\xi {\frac {di}{dt}},$

d’où nous tirons

(29)

$n{\frac {dj}{dt}}={\frac {k}{2}}(i+j)(n-2\Omega ).$

118.Réunissons dans un tableau les deux premières équations (25) et les équations (27), (28) et (29) :

(30)

$\left\{{\begin{aligned}{\frac {d\xi }{dt}}&=k(n-\Omega ),\\[0.75ex]{\frac {dn}{dt}}&=-k(n-\Omega ),\\[0.75ex]{\frac {de}{dt}}&={\frac {ke}{2\xi }}(11n-18\Omega ),\\[0.75ex]{\frac {di}{dt}}&=-{\frac {kn}{2\xi }}(i+j),\\[0.75ex]{\frac {dj}{dt}}&={\frac {k}{2n}}(i+j)(n-2\Omega ).\end{aligned}}\right.$

C’est de ces équations que nous allons tirer les variations des éléments.

119.Remarquons d’abord que les deux premières ne contiennent ni $e$ ni $i$. Elles donnent les variations de la rotation terrestre et de la distance moyenne de la Lune. Ce sont ces variations que nous avons discutées en détail dans la Section II. Rappelons les résultats de cette
fig.33. discussion. Prenant pour abscisse $\xi$ et pour ordonnée $n$ (fig. 33), nous traçons la droite

$\xi +n=h,$

et la courbe de rigidité

$n\xi ^{3}=1$

qui coupe la droite en deux points C et D. Le point représentatif $(\xi ,n)$ du système Terre-Lune est parti de C, état dans lequel le jour et le mois étaient tous deux égaux à 5^h36^m ; actuellement, ce point représentatif est en P$\,(\xi =3,2,\,n=0,8)\,;$ et l’état final sera représenté par D, où le jour redeviendra égal au mois, leur durée commune étant de 55 jours actuels.

120.Passons maintenant à la variation de l’excentricité $e$ donnée par la troisième équation (30). Il s’agit de savoir si ${\frac {de}{dt}}$ est positif ou négatif, pour reconnaître si l’excentricité $e$ croit ou décroît. Or, le signe de ${\frac {de}{dt}}$ dépend du signe de l’expression

$11n-18\Omega .$

Si

$11n-18\Omega >0,$

l’excentricité croît. Si, au contraire,

$11n-18\Omega <0,$

l’excentricité décroît. Traçons sur la figure 33 la courbe

$11n-18\Omega =0,$

c’est-à-dire la courbe

$n\xi ^{3}={\frac {18}{11}}.$

Cette courbe (représentée en trait ponctué) coupe la droite AE en deux points C′ et D′.

Lorsque le point représentatif ($\xi ,n$) parcourait le segment de droite CC′, on avait

$n\xi ^{3}<{\frac {18}{11}},$

c’est-à-dire

$11n-18\Omega <0\,;$

l’excentricité a donc commencé par décroître.

En P (étal actuel), on est entre C′ et D′, par suite

$11n-18\Omega >0,$

et l’excentricité est en train de croître.

Enfin, lorsque le point représentatif parcourra D′D, l’excentricité recommencera à décroître.

Si l’on trace la courbe (fig. 34) qui représente les variations de l’excentricité $e$ en fonction de $\xi$ (ce qui est possible puisqu’on connaît l’état actuel P), on constate que cette courbe présente une asymptote verticale correspondant à l’abscisse du point C et que l’excentricité $e$ passe par un minimum en C′, par un maximum en D′, puis décroît ensuite jusqu’au point final D où elle s’annule.

Il ne faudrait pas croire que l’asymptote verticale signifie que l’excentricité a été initialement très grande. Les équations (30), en effet, supposent essentiellement $e$ très petit et cessent d’être applicables dès que $e$ devient grand.

D’ailleurs, ce n’est pas ainsi que le problème se pose. Supposons que l’excentricité $e$ ait été initialement nulle, la troisième équation (30) donnerait

${\frac {de}{dt}}=0\,;$

donc

$e=0$

est une solution : elle correspond à une orbite circulaire restant indéfiniment circulaire^[14]. L’important est de savoir si cette solution est
fig.34. stable ou instable. Supposons que $e$ ait subi une petite variation : la troisième équation (30) étant de la forme

${\frac {de}{dt}}=\mathrm {M} e,$

la solution

$e=0$

sera stable ou instable, suivant que $\mathrm {M}$, c’est-à-dire

$11n-18\Omega ,$

sera négatif ou positif.

Donc, tant que le point représentatif (fig. 33) est situé entre C et C′, la solution

$e=0$

est stable ; l’orbite reste circulaire. Mais à partir du point C′ cette solution devient instable, et l’excentricité, ayant cessé d’être nulle par suite d’une petite perturbation quelconque, croît jusqu’en D′ ; puis, à partir de là, ${\frac {de}{dt}}$ devenant négatif, elle décroît jusqu’en D où elle s’annule.

La courbe représentative de l’excentricité (fig. 34) se composerait ainsi de la portion de droite cC′ et du morceau de courbe C′D′D.

Par suite, le fait qu’actuellement l’orbite lunaire est excentrique n’implique pas forcément qu’à l’origine l’excentricité était différente de zéro : le frottement des marées a pu, d’après Sir G. H. Darwin, faire naître une excentricité qui n’existait pas initialement.

121.Étudionsmaintenant les variations des inclinaisons $i$ et $j$, données par les deux dernières équations (30). Comme ce qui nous intéresse c’est l’angle $i+j$ que fait l’orbite avec l’équateur, nous ajoutons ces deux équations : il vient

(31)

${\frac {d(i+j)}{dt}}{\frac {k}{2}}(i+j)\left(1-2{\frac {\Omega }{n}}-{\frac {n}{\xi }}\right).$

Donc $\left(i+j\right)$ croîtra ou décroîtra suivant le signe de la quantité

$1-2{\frac {\Omega }{n}}-{\frac {n}{\xi }}=1-{\frac {2}{n\xi ^{3}}}-{\frac {n}{\xi }}.$

Remplaçant $n$ par $h-\xi ,$ cette quantité s’écrit (au facteur positif $n\xi ^{3}$ près)

$-2\xi ^{4}+3h\xi ^{3}-h^{2}\xi ^{2}-2\,;$

ce polynôme en $\xi$ présente deux variations de signe ; il a donc au plus deux racines positives. Dans le cas de la Lune, il a effectivement deux racines positives qui correspondent aux abscisses de deux certains points C′′ et D′′ situés entre C et D (fig. 33).

Nous pouvons donc faire pour l’inclinaison la même discussion que pour l’excentricité. Nous avons pour l’équation (31) la solution

$i+j=0.$

Cette solution est stable lorsque le point représentatif est entre C et C′′ ; elle devient instable entre C′′ et D′′. Si donc nous partons d’un état initial où l’inclinaison $i+j$ est nulle, l’inclinaison restera nulle au début ; puis, lorsque le point représentatif sera arrivé en C′′, si elle cesse d’être nulle par suite d’une petite perturbation quelconque, elle augmentera jusqu’en D′′ ; ensuite elle diminuera jusqu’en D où elle s’annulera de nouveau.

Nous voyons donc que le frottement des marées a pu faire naître une inclinaison du plan de l’orbite sur l’équateur, qui n’existait pas initialement.

122.Nous venons d’exposer, d’après Sir G. H. Darwin, l’évolution passée du système Terre-Lune. Mais quelle a pu être la durée de cette évolution ? Nos formules ne nous l’apprennent pas, car il y entre le coefficient de viscosité inconnu qu’avait la Terre quand elle était encore pâteuse. Néanmoins nous pouvons reconnaître facilement qu’il y a un maximum de l’action perturbatrice, c’est-à-dire un minimum de temps nécessaire.

Les seconds membres des formules (20^ter) sont de la forme

(32)

$\sum \mathrm {A} ^{2}\beta \sin 2\varepsilon .$

Les $\mathrm {A} ^{2}$ et les $\beta$ sont connus par la théorie des marées. Mais les $\sin 2\varepsilon$, définis par les équations

$\operatorname {tg} \varepsilon =k(2n+\beta \Omega ),$

sont inconnus puisque $k$ dépend de la viscosité. Or, un sinus est toujours inférieur à l’unité en valeur absolue. Nous exagérerons donc l’expression (32), par suite nous diminuerons le temps nécessaire à la variation de $\xi$, si nous remplaçons les $\sin 2\varepsilon$ par l’unité et si nous prenons tous les termes avec le même signe.

Époques	Durée du jour	Durée du mois (en jours actuels)	Incli- naison	Inverse de l’aplatis- sement	Distance (en rayons terrestres actuels)	ξ/n	Chaleur dégagée
0	23h56m	27,32	23°28'	232	60,4	'4,01'	0
46 300 000	15°30°	18,62	20°40'	96	46,8	'2,28'	225
56 600 000	9°55°	8,17	17°20'	40	27,0	'1,11'	760
56 800 000	7°50°	3,59	15°30'	25	15,6	'0,67'	1300
56 810 000	6°45°	1,58	14°25'	18	9,0	'0,44'	1760

C’est de cette façon qu’a procédé Sir G. H. Darwin pour introduire le temps dans son analyse. Il a dressé le Tableau ci-dessus, dans lequel la première colonne indique le nombre d’années écoulées à partir de l’époque actuelle, et en arrière (ces époques sont de plus en plus rapprochées à mesure qu’on remonte dans le passé, parce que, la Lune étant alors plus proche de la Terre, les effets des marées étaient plus considérables).

L’énergie mécanique du système Terre-Lune a toujours été en diminuant, le frottement la transformant en chaleur. Si cette chaleur avait été employée à échauffer la Terre, elle aurait élevé sa température d’un certain nombre de degrés (Fahrenheit) : c’est ce nombre de degrés qui figure à la dernière colonne du Tableau. Sir G. H. Darwin fait remarquer que l’on pourrait peut-être invoquer cette cause pour expliquer l’origine de la chaleur interne du globe.

123.Sir G. H. Darwin a aussi essayé de calculer une valeur du coefficient de viscosité inconnu de la Terre, en partant de l’accélération séculaire de la Lune. Des observations d’éclipses dans l’antiquité ont permis d’évaluer cette accélération à 10″. Or, le calcul indique une accélération théorique de 6″ seulement. Il y a donc une accélération de 4″ que la gravitation n’explique pas^[15]. Sir G. H. Darwin cherche, comme le fit autrefois Delaunay (n^o 95), à en rendre compte par l’augmentation du jour sidéral, due au frottement des marées. La Lune s’éloignant de la Terre subit réellement, non pas une accélération, mais un retard, et son accélération apparente ne serait due qu’à la différence entre le retard réel de la rotation terrestre et le retard réel de la révolution lunaire, le premier de ces deux retards étant plus grand que l’autre. C’est en égalant à 4″ la différence de ces deux retards, telle que la lui donnent ses formules, que Sir G. H. Darwin a calculé le coefficient de viscosité de l’intérieur de la Terre. Si l’on adoptait le coefficient ainsi obtenu, on trouverait pour la durée de l’évolution plusieurs milliards d’années ; mais il importe d’observer que la Terre a pu être autrefois beaucoup plus liquide qu’aujourd’hui.

124.Jusqu’ici, nous avons toujours adopté des unités particulières destinées à simplifier les formules. Cela était légitime, parce que nous étudiions l’action des marées produites par un même astre, la Lune, sur un même astre, la Terre. Mais si nous voulons maintenant comparer l’action des marées produites par divers astres sur un même astre, ou par un même astre sur divers astres (par exemple si nous envisageons le système formé par une planète et plusieurs satellites, ou bien le système formé par le Soleil et l’ensemble des planètes), il faudra rétablir les coefficients de proportionnalité. C’est ce que nous allons faire.

125.De même que la marée lunaire a une influence sur la longueur du jour et du mois, la marée solaire a une influence sur la longueur du jour et de l’année. Désignons par $\mathrm {S} ,$ $\mathrm {L} ,$ $\mathrm {T}$ les masses du Soleil, de la Lune, de la Terre. Nous appelons toujours

$\mathrm {C}$	le moment d’inertie de la Terre,
$n$	sa vitesse angulaire de rotation,
$\Omega$	la vitesse de révolution de la Lune,
$a$	le demi-grand axe de son orbite.

L’équation des aires, appliquée au système Terre-Lune, supposé seul, s’écrit

(33)

$\mathrm {L} a^{2}\Omega +\mathrm {C} n={\text{const.}}$

$\mathrm {C} n$ représente le moment de rotation dû à la rotation terrestre, $\mathrm {L} a^{2}\Omega$ le moment de rotation dû au mouvement orbital de la Lune. Le moment de rotation dû au mouvement orbital de la Terre autour du centre de gravité du système Terre Lune étant très petit, nous le négligeons à côté de $\mathrm {L} a^{2}\Omega$. Quant à celui qui est dû à la rotation de la Lune sur elle-même, nous en faisons abstraction, envisageant ici la Lune comme un simple point matériel sans dimensions.

Écrivons maintenant l’équation des aires pour le système Terre-Soleil, supposé seul. Appelant

$\Omega '$	la vitesse de révolution de la Terre autour du Soleil,
$a'$	le demi-grand axe de l’orbite terrestre,

nous aurons

(34)

$\mathrm {T} a'^{2}\Omega '+\mathrm {C} n={\text{const.}}$

$\mathrm {C} n$ représente toujours le moment de rotation dû à la rotation terrestre ; $\mathrm {T} a'^{2}\Omega '$ représente le moment de rotation dû au mouvement orbital de la Terre autour du Soleil, à côté duquel celui qui est dû au mouvement orbital du Soleil, autour du centre de gravité du système Terre-Soleil, est négligeable. Nous faisons aussi abstraction du moment de rotation dû à la rotation du Soleil sur lui-même, envisageant ici le Soleil comme un simple point matériel, ou, si l’on préfère, comme une sphère absolument rigide dont le moment de rotation est constant.

Transformons les équations (33) et (34), en introduisant les quantités

$\xi =\Omega ^{-{\frac {1}{3}}},\qquad \xi '=\Omega '^{-{\frac {1}{3}}},$

et en nous servant de la troisième loi de Képler qui donne

${\begin{aligned}a^{3}\Omega ^{2}&=\mathrm {T} ,\\[0.5ex]a'^{3}\Omega '^{2}&=\mathrm {S} .\end{aligned}}$

Les équations des aires (33) et (34) s’écrivent alors

${\begin{alignedat}{3}\mathrm {LT} ^{\frac {2}{3}}\xi &{}+{}&\mathrm {C} n&={\text{const.}},\\[0.75ex]\mathrm {TS} ^{\frac {2}{3}}\xi '&{}+{}&\mathrm {C} n&={\text{const.}}.\end{alignedat}}$

Considérons d’abord l’action de la marée lunaire. Cette marée donne, pendant un certain temps $\tau$, à la rotation $n$ de la Terre une variation $\delta n$, et il en résulte pour $\xi$ une variation $\delta \xi$ donnée par

(35)

$\mathrm {LT} ^{\frac {2}{3}}\,\delta \xi +\mathrm {C} \,\delta n=0.$

De même, la marée solaire fait, dans le même temps $\tau$, subir à $n$ une variation $\delta 'n,$ et il en résulte pour $\xi '$ une variation $\delta '\xi '$ donnée par

(36)

$\mathrm {TS} ^{\frac {2}{3}}\,\delta '\xi '+\mathrm {C} \,\delta 'n=0.$

Comparons $\delta 'n$ à $\delta n$ : il s’agit de l’action de deux marées différentes sur un même astre, la Terre. Le rapport de $\delta 'n$ à $\delta n$ sera donc approximativement égal au rapport ${\frac {\mathrm {A} '^{2}}{\mathrm {A} ^{2}}}$ des carrés des coefficients des deux marées. La marée solaire est environ trois fois moindre que la marée lunaire. On a donc

${\frac {\delta 'n}{\delta n}}={\frac {\mathrm {A} '^{2}}{\mathrm {A} ^{2}}}=\left({\frac {1}{3}}\right)^{2}={\frac {1}{9}}.$

L’augmentation de la durée du jour provenant de la marée solaire est donc environ 9 fois moindre que celle qui provient de la marée lunaire.

Les équations (35) et (36) donnent ensuite

${\frac {\delta '\xi '}{\delta \xi }}={\frac {1}{9}}{\frac {\mathrm {LT} ^{\frac {2}{3}}}{\mathrm {TS} ^{\frac {2}{3}}}}\,;$

or, le second membre est extrêmement petit ; $\delta '\xi '$ est donc incomparablement plus petit que $\delta \xi$ ; ce qui signifie que la marée solaire n’a qu’une influence insignifiante sur la distance moyenne de la Terre au Soleil, c’est-à-dire sur la longueur de l’année.

126.Les marées que la Lune soulève sur la Terre ralentissent la rotation terrestre. De même les marées que la Terre pourrait soulever sur la Lune exerceraient une influence sur la rotation de la Lune. Actuellement, la Terre ne soulève pas de marées sur la Lune, puisque la Lune nous présente toujours le même hémisphère. Mais aux époques reculées, la Terre a dû soulever des marées sur son satellite, et c’est précisément, ainsi que l’avait déjà affirmé Laplace, à l’action de ces marées qu’est due l’égalité actuelle de la durée de rotation et de la durée de révolution de la Lune.

Soit $\mathrm {M}$ la masse de l’astre perturbateur qui produit la marée sur un astre sphérique T de rayon $a$ (fig. 35). Appelons $c$ la distance
fig.35. TM du centre de la sphère T à l’astre perturbateur et $r$ la distance MA de l’astre perturbateur à un point A de la surface de l’astre T. Le potentiel dû à l’astre perturbateur est

${\begin{aligned}{\frac {\mathrm {M} }{r}}&={\frac {\mathrm {M} }{c}}\left(1-2{\frac {a}{c}}\cos \sigma +{\frac {a^{2}}{c^{2}}}\right)^{-{\frac {1}{2}}}\\[0.75ex]&={\frac {\mathrm {M} }{c}}+{\frac {\mathrm {M} a}{c^{2}}}\cos \sigma +{\frac {\mathrm {M} a^{2}}{c^{3}}}{\frac {3\cos ^{2}\sigma -1}{2}}\\[0.75ex]&=\mathrm {\mathrm {U} _{0}+\mathrm {U} _{1}+\mathrm {U} _{2}} .\end{aligned}}$

Le potentiel générateur de la marée est

$\mathrm {U} _{2}={\frac {\mathrm {M} a^{2}}{c^{3}}}{\frac {3\cos ^{2}\sigma -1}{2}},$

il est proportionnel à

${\frac {\mathrm {M} a^{2}}{c^{3}}}\,\cdot$

La dénivellation statique est

$\zeta ={\frac {\mathrm {U} _{2}}{g}},$

elle est proportionnelle à

${\frac {\mathrm {M} a^{2}}{c^{3}g}}.$

Le bourrelet liquide, dû à cette dénivellation, produit sur l’astre M un potentiel perturbateur

$\mathrm {W} =\mathrm {M} w\,\iint {\frac {\zeta \,d\sigma }{r}}\,,$

où $w$ désigne la densité du bourrelet liquide soulevé sur l’astre T. Or, nous avons, le signe $\propto$ indiquant la proportionnalité,

${\begin{aligned}\zeta &\propto {\frac {\mathrm {M} a^{2}}{c^{3}g}},\\[0.5ex]d\sigma &\propto a^{2},\end{aligned}}$

et ${\frac {\mathrm {M} }{r}}$ peut, sous le signe $\iint$ être remplacé par $\mathrm {U} _{2}$^[16] qui est proportionnel à ${\frac {\mathrm {M} a^{2}}{c^{3}}}.$ Nous pouvons donc écrire

$\mathrm {W} \propto {\frac {\mathrm {M} ^{2}a^{6}w}{c^{6}g}}.$

Le couple $\Gamma$ qui fait varier la rotation de l’astre T est proportionnel à

${\frac {d\mathrm {W} }{d\chi }},$

puisque

${\frac {d\mathrm {W} }{d\chi }}\,d\chi$

représente le travail virtuel produit dans une petite rotation $d\chi$ de la sphère T.

Comme ${\frac {d\mathrm {W} }{d\chi }}$ est lui-même proportionnel à $\mathrm {W}$^[17] le couple $\Gamma$ est proportionnel à

${\frac {\mathrm {M} ^{2}a^{6}w}{c^{6}g}}.$

Si, maintenant, nous tenons compte de la viscosité de l’astre T, nous trouvons

couple perturbateur $\Gamma \propto {\frac {\mathrm {M} ^{2}a^{6}w}{c^{6}g}}\sin 2\varepsilon .$

La dérivée ${\frac {dn}{dt}}$ de la vitesse de rotation de l’astre T s’obtiendra en divisant le couple perturbateur $\Gamma$ par le moment d’inertie de la sphère T qui est proportionnel à $wa^{5}$

Bref, nous aurons

${\frac {dn}{dt}}\propto {\frac {\mathrm {M} ^{2}a}{c^{6}g}}\sin 2\varepsilon .$

L’angle $\varepsilon$ est défini par l’équation

$\operatorname {tg} \varepsilon =k\alpha ,$

$k$ étant une constante proportionnelle à la viscosité et $\alpha$ étant proportionnel à la vitesse de la marée. Pour la marée principale semi-diurne, on trouve, en faisant le calcul,

$\operatorname {tg} \varepsilon =19\,\nu \,{\frac {n-\Omega }{gaw}},$

$\nu$ étant le coefficient de viscosité de l’astre T. Comme l’angle $\varepsilon$ est très petit (en prenant pour $\nu$ le coefficient de viscosité de la poix, ou trouve que cet angle un dépasse pas 10″ pour le système Terre-Lune), nous pouvons écrire

$\sin 2\varepsilon \propto \operatorname {tg} \varepsilon \propto {\frac {n-\Omega }{gaw}}.$

Or, nous avons pour la gravite $g$, à la surface de l’astre T

$g\propto {\frac {wa^{3}}{a^{2}}}\propto wa,$

et par suite

$\sin 2\varepsilon \propto {\frac {n-\Omega }{g^{2}}}\propto {\frac {n-\Omega }{a^{2}w^{2}}}\,\cdot$

Finalement, il vient

${\frac {dn}{dt}}\propto {\frac {\mathrm {M} ^{2}a}{c^{6}g}}{\frac {n-\Omega }{g^{2}}}\propto {\frac {\mathrm {M} ^{2}(n-\Omega )}{c^{6}w^{3}a^{2}}}\,\cdot$

Si la sphère T est la Terre et l’astre M la Lune, ces proportionnalités représentent la diminution de la rotation terrestre due à la marée lunaire.

Si, maintenant, nous voulions avoir la diminution ${\frac {dn'}{dt}}$ de la rotation de la Lune, due aux marées que la Terre produit sur la Lune, nous aurions

${\frac {dn'}{dt}}\propto {\frac {\mathrm {M} '^{2}(\omega -\Omega )}{c^{6}w'^{3}a'^{2}}}.$

où $\mathrm {M} '$ désigne cette fois la masse de la Terre, $w'$ et $a'$ la densité et le rayon de la Lune, $\omega$ sa vitesse angulaire de rotation.

Actuellement, les durées de rotation et de révolution de la Lune étant les mêmes, $\omega -\Omega$ est nul et il en est de même de ${\frac {dn'}{dt}}\,:$ l’action retardatrice de la Terre sur la Lune est épuisée. Mais il n’en a pas toujours été ainsi : à l’origine $\omega -\Omega$ était comparable à $n-\Omega$, et alors on avait

${\frac {\dfrac {dn'}{dt}}{\dfrac {dn}{dt}}}\propto \left({\frac {\mathrm {M} '}{\mathrm {M} }}\right)^{2}\left({\frac {w}{w'}}\right)^{3}\left({\frac {a}{a'}}\right)^{2},$

ce qui, puisque

${\begin{aligned}\mathrm {M} &\propto w'a'^{3},\\\mathrm {M} '&\propto w\,a^{3},\end{aligned}}$

s’écrit

${\frac {\dfrac {dn'}{dt}}{\dfrac {dn}{dt}}}\propto \left({\frac {w}{w'}}\right)^{5}\left({\frac {a}{a'}}\right)^{8}.$

Comme les densités $w$ et $w'$ de la Terre et de la Lune sont du même ordre, ce rapport est comparable à

$\left({\frac {a}{a'}}\right)^{8}={}$ 32 000 environ.

Donc l’action retardatrice de la Terre sur la Lune a dû être au début environ 32 000 fois plus forte que l’action retardatrice de la Lune sur la Terre. On conçoit donc que cette action ait pu être assez puissante pour avoir arrêté le mouvement de rotation de la Lune relativement à la Terre, et pour avoir forcé notre satellite à nous tourner toujours la même face.

127.Si, maintenant, on étudie le système formé par le Soleil et les différentes planètes, ou constate d’abord que l’action produite sur la rotation du Soleil par les marées que les planètes soulèvent sur le Soleil est tout à fait insignifiante. Quant à l’action retardatrice de la marée solaire sur la rotation des différentes planètes, son coefficient de proportionnalité est

${\frac {\mathrm {M} ^{2}a}{c^{6}g}}{\frac {n-\Omega }{g^{2}}}\,,$

ce qui peut s’écrire

${\frac {\mathrm {M} ^{2}an}{c^{6}g^{3}}},$

en négligeant la vitesse angulaire $\Omega$ de révolution de la planète, à côté de sa vitesse angulaire $n$ de rotation.

Or, $\mathrm {M}$, masse du Soleil, est le même pour toutes les planètes, et l’on a

$g\propto {\frac {m}{a^{2}}},$

$m$ étant la masse de la planète envisagée. Le coefficient de proportionnalité auquel est proportionnel ${\frac {dn}{dt}}$ est donc pour chaque planète

${\frac {a^{7}n}{c^{6}m^{3}}}.$

Sir G. H. Darwin donne le Tableau suivant (où $\mathrm {C}$ représente le moment d’inertie de la planète) :

Planètes	$\mathrm {C} {\tfrac {dn}{dt}}$	${\tfrac {dn}{dt}}$
Mercure	9,10000	1 000,00002
Vénus	8.1	11,00002
La Terre	1	1,00002
Mars	0,026	0,89002
Jupiter	2,3	0,00005
Saturne	0,11	0,00002

Le calcul, en ce qui concerne Mercure et Vénus, a été fait en supposant à ces deux planètes une durée de rotation de 24 heures. On voit que, pour ces planètes intérieures, l’action retardatrice de la marée solaire est forte. S’il est vrai, comme le prétendent plusieurs observateurs, que ces deux planètes tournent toujours une même face vers le soleil^[18], ce fait pourrait s’expliquer par l’action retardatrice de la marée solaire. La théorie expliquerait aussi pourquoi les planètes extérieures Uranus et Neptune, n’ayant subi qu’une marée solaire très faible, ont conservé leur rotation rétrograde.

IV. Influence accélératrice du refroidissement.

128.Le refroidissement séculaire de la Terre la contracte et diminue son moment d’inertie ; par suite, en vertu de la loi des aires, sa vitesse de rotation doit s’accroître de ce chef. Il y a donc lieu, à côté de l’influence retardatrice des marées, étudiée dans les pages précédentes, de tenir compte de l’influence accélératrice du refroidissement.

Nous avons vu plus haut (n^o 126) que le couple retardateur $\Gamma$ dû à la marée est proportionnel à

${\frac {\mathrm {M} ^{2}a^{6}w}{c^{6}g}}\sin 2\varepsilon .$

c’est-à-dire à

${\frac {\mathrm {M} ^{2}a^{6}w}{c^{6}g^{3}}}(n-\Omega ),$

ou encore à

${\frac {\mathrm {M} ^{2}a^{9}}{c^{6}m^{2}}}(n-\Omega ).$

Or, $\mathrm {M}$ (masse de la Lune) et $m$ (masse de la Terre) sont des constantes, et nous regarderons aussi $c$ (distance de la Lune à la Terre) comme constant. Par suite, le couple $\Gamma$ est proportionnel à

$a^{9}(n-\Omega ).$

Le moment de rotation $\mathrm {C} n$ de la Terre aura sa dérivée ${\frac {d(\mathrm {C} n)}{dt}}$ proportionnelle au couple $\Gamma$ : nous aurons donc l’équation

${\frac {d(\mathrm {C} n)}{dt}}=-\mathrm {A} a^{9}(n-\Omega ),$

$\mathrm {A}$ étant une certaine constante positive.

Comme $\mathrm {C}$, moment d’inertie de la Terre, est proportionnel au carré $a^{2}$ de son rayon, nous pouvons écrire l’équation précédente ainsi

${\frac {d(a^{2}n)}{dt}}=-\mathrm {B} a^{9}(n-\Omega ),$

$\mathrm {B}$ étant une nouvelle constante positive. De là nous tirons

(37)

${\frac {dn}{dt}}=-{\frac {2n}{a}}{\frac {da}{dt}}-\mathrm {B} a^{7}(n-\Omega ).$

Par suite du refroidissement, le rayon terrestre $a$ diminue, et ${\frac {da}{dt}}$ est négatif ; donc, au second membre de l’équation (37), nous avons un terme positif dû au refroidissement séculaire, et un terme négatif dû au frottement de la marée.

Posons

${\frac {dn}{dt}}=-\lambda a,$

$\lambda$ étant une quantité positive. L’équation (37) s’écrit

(38)

${\frac {dn}{dt}}=n(2\lambda -\mathrm {B} a^{7})+\mathrm {B} a^{7}\Omega .$

Nous allons tout d’abord supposer, à seule fin de faciliter les calculs, que le refroidissement suit la loi particulière indiquée par la formule

$2\lambda =\mu a^{7},$

$\mu$ étant une constante : nous aurons alors

${\frac {da}{dt}}=-{\frac {\mu }{2}}a^{8},$

d’où

${\frac {da}{a^{8}}}=-{\frac {\mu }{2}}\,dt,$

et

${\frac {1}{7a^{7}}}={\frac {\mu }{2}}(t-t_{0})\,;$

le rayon terrestre, avec cette loi, varierait comme l’inverse de la racine septième du temps. L’équation (38) s’écrit alors

${\frac {1}{a^{7}}}\,{\frac {dn}{dt}}=n(\mu -\mathrm {B} )+\mathrm {B} \Omega .$

Si l’on a

$\mu >\mathrm {B} ,$

$n$ ira constamment en croissant, et tendra vers $\pm \infty ,$ suivant son signe.

Si l’on a

$\mu <\mathrm {B} ,$

$n$ tendra vers une limite finie qui sera atteinte lorsque ${\frac {dn}{dt}}$ s’annulera, c’est-à-dire lorsqu’on aura

${\frac {n}{\Omega }}={\frac {-\mathrm {B} }{\mu -\mathrm {B} }}.$

Cette rotation finale est directe (de même signe que $\Omega$), puisque le second membre est positif.

129.Appliquons cette loi du refroidissement à l’étude de l’évolution d’une nébuleuse planétaire qui se transforme en planète. Nous avons vu (Chap. III, n^o 42) qu’au début de son existence, lorsqu’elle vient de se former aux dépens d’un anneau de Laplace, la rotation d’une telle nébuleuse planétaire est rétrograde.

Alors, si

$\mu >\mathrm {B} ,$

l’effet du refroidissement l’emporte sur celui des marées : la rotation reste toujours rétrograde et tend même à s’accélérer. C’est ce qui a pu arriver pour les systèmes extérieurs d’Uranus et de Neptune.

Si

$\mu <\mathrm {B} ,$

la rotation, d’abord négative, a varié en tendant vers la limite finale

${\frac {-\mathrm {B} \Omega }{\mu -\mathrm {B} }},$

qui est positive. Si $\mu$ est inférieur à $\mathrm {B}$, mais très voisin de $\mathrm {B}$, cette vitesse angulaire finale est très grande. On peut penser que ce cas s’est présenté pour Jupiter et Saturne, car leur rotation est directe et très rapide.

Pour les planètes plus voisines du Soleil, $\mathrm {B} -\mu$ croît puisque l’influence de la marée solaire se fait sentir davantage. La rotation finale est moins rapide.

Enfin, pour les planètes très voisines du Soleil (Mercure et Vénus) (tout au moins dans l’opinion de M. Schiaparelli), $\mu$ est négligeable devant $\mathrm {B}$ et la vitesse limite de rotation est

$\mathrm {B} =\Omega \,;$

elle est égale à la vitesse de révolution.

130.Pour une loi de refroidissement autre que celle que nous avons envisagée pour simplifier, au lieu d’être une constante, serait variable et $n$ tendrait toujours à se rapprocher de

${\frac {-\mathrm {B} \Omega }{\mu -\mathrm {B} }}$

si $\mu <\mathrm {B}$, et à s’en éloigner si $\mu >\mathrm {B}$.

Lord Kelvin estime que la variation séculaire de la durée du jour, due au refroidissement, serait de 1/30 de seconde. Cette accélération est très petite à côté du retard qui serait dû à l’influence de la marée. On doit donc penser que, pour la Terre, l’effet du frottement de la marée interne l’emporte sur celui du refroidissement, et que la vitesse angulaire $n$ de rotation de la Terre est actuellement en voie de décroissance.

131.Une troisième cause peut modifier la rotation de la Terre. Cette cause, c’est l’augmentation de la masse de la Terre par suite de la pluie météorique, de la chute d’étoiles filantes dont elle est bombardée. Ces projectiles qui tombent sur la Terre viennent augmenter son moment d’inertie et, par conséquent, retarder sa rotation. On a dit qu’il suffirait, pour expliquer les 4″ d’accélération séculaire de la Lune dont la gravitation ne rend pas compte, d’admettre que le rayon de la Terre s’accroît de 1 mètre en 10 000 ans, par suite de la chute des météores. Mais un tel accroissement du rayon terrestre représente une pluie météorique vraiment énorme et inadmissible.

V. — Hypothèse sur la formation de la Lune.

132.Nous avons dit que, d’après Sir G. H. Darwin, la Lune à sa naissance était très voisine de la Terre. Mais comment la Lune a-t-elle pu naître de la Terre ?

On peut d’abord supposer, restant dons l’ordre d’idées de Laplace qu’elle s’est formée aux dépens d’un anneau abandonné par la nébuleuse terrestre.

On peut aussi — c’est là une hypothèse proposée par Sir G. H. Darwin — penser que la Terre encore liquide subissait la marée solaire : il est arrivé un moment ou la période propre d’oscillation de cette masse fluide est devenue égale à la période de la marée solaire. Alors l’amplitude de la marée s’est exagérée par suite du phénomène de résonnance : l’intumescence est devenue énorme, et une portion de la masse se serait détachée de la Terre, lui formant un satellite.

Mais une autre hypothèse, que nous allons examiner maintenant, est encore admissible.

133.Rappelons ce que nous avons dit relativement aux figures d’équilibre d’une masse fluide homogène soumise à l’attraction mutuelle de ses parties et tournant avec une vitesse angulaire constante $\omega$ autour d’un axe $ox$ (n^o 47). Nous avons comme figures d’équilibre possibles :

1^o Des ellipsoïdes de révolution aplatis, dits ellipsoïdes de Mac-Laurin ;

2^o Des ellipsoïdes à trois axes inégaux, dits ellipsoïdes de Jacobi. Reprenant les notations du n^o 45, nous appelons $a,b,c$ les trois demi-axes de l’ellipsoïde qui est une figure d’équilibre, et nous posons

$s={\frac {a^{2}}{b^{2}}},\qquad t={\frac {a^{2}}{c^{2}}}.$

Nous avons vu que $s$ et $t$ sont compris entre 0 et 1, c’est-à-dire que l’axe de rotation est toujours le plus petit axe de l’ellipsoïde, et que dans le plan des $s,t,$ la courbe lieu du point $\left(s,t\right)$ représentatif de l’ellipsoïde se compose, à l’intérieur du carré

${\begin{aligned}0<s&<1\\0<t&<1,\\\end{aligned}}$

de la droite OA, et d’une ligne DB (fig. 36). La droite OA correspond
fig.36. aux ellipsoïdes de Mac-Laurin, la courbe DB correspond aux ellipsoïdes de Jacobi,

Si l’on examine comment varie la vitesse angulaire $\omega$ lorsqu’on chemine sur ces deux portions de courbe, on constate qu’au point A où l’ellipsoïde de Mac-Laurin est une sphère, la vitesse $\omega$ est nulle ; lorsqu’on décrit la droite AO dans le sens AO, $\omega$ croît jusqu’à un certain point E où il est maximum, puis décroît jusqu’en O où il s’annule de nouveau. Si, maintenant, on décrit l’arc DB qui correspond aux ellipsoïdes à axes inégaux, $\omega$ part de zéro en D, croît jusqu’en C où il passe par un maximum, puis décroît jusqu’en B où il s’annule. Deux points tels que M et M′, symétriques par rapport à OA, représentent le même ellipsoïde de Jacobi, ayant simplement tourné de 90°.

Mais ces figures ellipsoïdales d’équilibre, de Mac-Laurin ou de Jacobi, ne sont pas les seules possibles pour notre masse fluide homogène animée d’un mouvement de rotation ; il en existe une infinité d’autres^[19] dont nous allons maintenant parler.

134.Rappelons la définition des coordonnées elliptiques de l’espace. Considérons la famille de quadriques homofocales

${\frac {x^{2}}{\lambda ^{2}-a^{2}}}+{\frac {y^{2}}{\lambda ^{2}-b^{2}}}+{\frac {z^{2}}{\lambda ^{2}-c^{2}}}-1=0.$

Par chaque point de l’espace passent trois de ces surfaces : en effet, $x,y,z$ étant donnés, on a pour déterminer $\lambda ^{2}$ une équation du troisième degré, dont les racines sont séparées par les nombres $a^{2},$ $b^{2},$ $c^{2}.$ Appelant $\rho ^{2},$ $\mu ^{2},$ $\nu ^{2},$ ces trois racines, nous aurons

$\rho ^{2}>a^{2}>\mu ^{2}>b^{2}>\nu ^{2}>c^{2}.$

La plus grande racine $\rho ^{2}$ correspond à un ellipsoïde, la racine moyenne $\mu ^{2}$ à un hyperboloïde à une nappe, la plus petite $\nu ^{2}$ à un hyperboloïde à deux nappes.

Réciproquement, si $\rho ,\mu ,\nu$ sont donnés, on a trois surfaces se coupant en huit points placés symétriquement, par rapport aux divers plans de coordonnées. Si on ne considère que les points situés dans le trièdre positif des axes de coordonnées, les trois nombres $\rho ,\mu ,\nu$ définissent un point et un seul : ce sont les coordonnées elliptiques de l’espace.

Soit $\mathrm {R}$ une fonction de $\rho$ qui sera, soit un polynôme en $\rho ^{2}$, soit un tel polynôme multiplié par un, deux ou trois des radicaux

${\sqrt {\rho ^{2}-a^{2}}},\qquad {\sqrt {\rho ^{2}-b^{2}}},\qquad {\sqrt {\rho ^{2}-c^{2}}}.$

Soient $\mathrm {M}$ la même fonction de $\mu$ et $\mathrm {N}$ la même fonction de $\nu$. $\mathrm {M}$ et $\mathrm {N}$ ne diffèrent de $\mathrm {R}$ que par le changement de $\rho ^{2}$ en $\mu ^{2}$ et en $\nu ^{2}$ respectivement.

Le produit $\mathrm {RMN}$ est une fonction de $x,y,z$. Si cette fonction est harmonique, c’est-à-dire si l’on a

$\left({\frac {d^{2}}{dx^{2}}}+{\frac {d^{2}}{dy^{2}}}+{\frac {d^{2}}{dz^{2}}}\right)\mathrm {RMN} =0,$

les fonctions $\mathrm {R} ,$ $\mathrm {M} ,$ $\mathrm {N}$ sont dites fonctions de Lamé. On démontre qu’il existe effectivement une infinité de fonctions de Lamé.

Considérons un ellipsoïde E correspondant à une valeur donnée $\rho$ du paramètre, et définissons une surface $\Sigma$ voisine de l’ellipsoïde E
fig.37. (fig. 37) : en chaque point de E nous menons une petite normale PP′ de longueur

$\zeta =\varepsilon \,l\,\mathrm {MN} ,$

en posant

$l={\frac {1}{\sqrt {\left(\rho ^{2}-\mu ^{2}\right)\left(\rho ^{2}-\nu ^{2}\right)}}}\,;$

$l$ est une fonction bien déterminée du point quelconque P de l’ellipsoïde E ; $\mathrm {M}$ et $\mathrm {N}$ sont deux fonctions de Lamé conjuguées ; $\varepsilon$ est une constante très petite.

Le lieu du point P’ est une surface $\Sigma$ qui coupe l’ellipsoïde E suivant des lignes de courbure : en effet, le long de l’intersection de ces deux surfaces, on a

$\zeta =0,$

c’est-à-dire

$\mathrm {M} =0\qquad {\text{ou}}\qquad \mathrm {N} =0\,;$

c’est dire que cette intersection est située sur un hyperboloïde

$\mu =\,{\text{const.}}\qquad {\text{ou}}\qquad \nu =\,{\text{const.}}$

hyperboloïde qui, on le sait, coupe E suivant une ligne de courbure.

135.Revenons maintenant à nos ellipsoïdes de Mac-Laurin et de Jacobi, figures d’équilibre d’une masse fluide homogène en rotation. On peut démontrer qu’il existe une infinité d’ellipsoïdes de Mac-Laurin, correspondant à des points N₁, N₂, N₃, …,^[20] de la droite AO (fig. 36), tels qu’une surface voisine Σ définie comme nous venons de le faire soit aussi une figure d’équilibre. De même, il existe une infinité d’ellipsoïdes de Jacobi, correspondant à des points M, M₁, M₂, …, M′, M′₁, M′₂, …, de la courbe DB, tels qu’une surface voisine Σ soit aussi une figure d’équilibre.

136.Parlons maintenant de la stabilité de nos figures d’équilibre. On démontre que les ellipsoïdes de Mac-Laurin sont stables de A en C et instables de C en O (fig.. 36). Pour les ellipsoïdes de Jacobi, il suffit d’examiner la demi-courbe CB : ils sont stables depuis C jusqu’au point M où l’on rencontre pour la première fois une figure Σ. ils sont instables de M en B.

Quant aux figures d’équilibre Σ voisines des ellipsoïdes, un démontre qu’elles sont toutes instables, sauf peut-être une seule, celle qui correspond justement au point M où l’ellipsoïde de Jacobi cesse d’être stable.

137.Considérons alors une masse fluide homogène animée originairement d’un mouvement de rotation et se refroidissant lentement. Si le refroidissement est assez lent, le frottement interne détermine la révolution de l’ensemble dans toutes ses parties avec la même vitesse angulaire. Le moment de rotation demeurera d’ailleurs constant.

Au début, la densité étant très faible, la figure de la masse est un ellipsoïde de révolution peu différent d’une sphère. Le refroidissement aura d’abord pour effet d’augmenter l’aplatissement de l’ellipsoïde qui restera cependant de révolution. Le point représentatif (fig. 36) décrira la portion de droite AC qui correspond aux ellipsoïdes de Mac-Laurin, et cela jusqu’en C où les ellipsoïdes de Mac-Laurin cessent d’être stables. Le point représentatif ne pouvant pas prendre le chemin CO prendra alors, par exemple, la direction CM ; l’ellipsoïde deviendra à trois axe inégaux, et cela jusqu’en M où les ellipsoïdes de Jacobi cessent d’être stables. À partir de là, la masse ne peut plus conserver la forme ellipsoïdale puisque celle-ci est devenue instable : elle prendra alors la seule forme possible, celle de la surface Σ voisine de l’ellipsoïde. Cette surface Σ (fig. 37) présente une figure piriforme, offrant comme un étranglement dans la région marquée 3, tandis que les régions 2 et 4 tendent à se renfler aux dépens des régions 1 et 3, comme si la masse cherchait à se diviser en deux masses inégales.

Il est difficile d’annoncer ce qui arrivera ensuite. On peut penser que la masse ira en se creusant de plus en plus dans la région 3 et finira par se partager en deux corps isolés.

La figure piriforme Σ, avons-nous dit, est peut-être stable ; mais il n’est pas certain qu’elle le soit réellement. Sir G. H. Darwin a trouvé que cette figure est stable, mais, d’après M. Liapounoff elle serait instable. Pour trancher la question il faudrait recommencer le calcul ; or, ce calcul est extrêmement pénible.

Si cette figure Σ est instable, la rupture, la séparation de la masse fluide en deux masses inégales, au lieu d’être progressive, se produirait d’un seul coup et brusquement.

138.Quelles conclusions pouvons-nous tirer, au point de vue cosmogonique, de la discussion précédente ? Il est impossible de voir là une origine, même approchée, des planètes : car les planètes n’ont qu’une masse insignifiante relativement à celle du Soleil. Mais Sir G. H. Darwin estime^[21] que certains satellites ont pu su former de cette façon aux dépens du leur planète. Cela aurait pu arriver notamment pour le système Terre-Lune dans lequel les deux masses sont comparables, l’une n’étant pas une fraction extrêmement petite de l’autre. La Lune, s’étant ainsi détachée de la Terre, aurait décrit autour d’elle une orbite de très petit rayon ; mais, par suite du frottement des marées, ce rayon aurait été en augmentant, ainsi qu’il a été expliqué.

On pourrait concevoir de la même façon la formation de certaines étoiles doubles, dont les composantes ont des masses du même ordre de grandeur.

1. Les travaux de Sir G. H. Darwin sur ce sujet forment l’objet d’une série de Mémoires publiés dans les Philosophical Transactions et dans les Proceedings of the Royal Society de 1879 à 1882. Ils se trouvent réunis dans G. H. Darwin’s Scientific Papers, dont ils forment l’ensemble du volume II intitulé Tidal friction and Cosmogony (Cambridge, 1908). Voir aussi C. Wolf : Les Hypothèses Cosmogoniques, Chap. VI, p. 75.
2. Ici, la Lune L est regardée, pour simplifier, comme un simple point matériel sans dimensions.
3. L’attraction $\mathrm {R'}$ de la Terre sur la Lune (fig. 25) se décompose en : 1^o une force centrale presque égale à la force entière et donnant le mouvement képlérien, et 2^o une force perturbatrice $\mathrm {F}$ perpendiculaire au rayon vecteur.
4. Voir M. Lévy : Leçon sur la théorie des Marées, t. I, chap. I ; et H. Poincaré : Leçons de Mécanique céleste, t. III, Théorie des Marées, chap. I et III.
5. Dans $\mathrm {V} _{0}$ il est tenu compte de la force centrifuge qui provient de la rotation diurne. Nous négligeons le potentiel dû à la couche d’eau comprise entre la surface moyenne et la surface vraie des mers.
6. $\zeta$ sera fonction du temps par l’intermédiaire de $\rho ,$ $\delta '$ et ${\mathcal {A}}.$ Observons que les coordonnées $\rho$ et $\delta '$ de l’astre varient très lentement, tandis que son angle horaire ${\mathcal {A}}$ varie vite.
7. On reconnaît aisément que l’intégrale
   $\iint \mathrm {X} ^{2}\,d\sigma$

   étendue à toute la sphère a, comme nous le désirions, la même valeur $\mathrm {K}$ pour toutes ces fonctions sphériques $\mathrm {X}$.

8. Rappelons que l’angle $\varepsilon$ est très petit et peut être confondu avec sa tangente ou son sinus (n^o 107)).
9. Voir H. Poincaré ; Leçons de Mécanique Céleste, t. I, Chap. III.
10. Ce sont celles qui ont été désignées par
    $\mathrm {L} ,\,\mathrm {G} ,\,\Theta ,\,l,\,g,\,\theta ,$

    à la p. 76 de l’Ouvrage de M. H. Poincaré : Leçons de Mécanique Céleste, t. I. Dans les trois premières de ces variables, nous faisons abstraction d’un même facteur constant où figurent les masses de la Terre et de la Lune.

11. Excepté pour les termes sidéraux. Ces termes sidéraux n’ont d’ailleurs d’influence que sur l’inclinaison, et cette influence est faible.
12. Voir Maurice Lévy : Leçons sur la Théorie des Marées, t. I, Ch. III, et H. Poincaré: Leçons de Mécanique Céleste, t. III, Théorie des Marées, Ch. II. Nous faisons ici abstraction d’un facteur constant, le même pour tous les termes. Et nous laissons de côté les termes évectionnels et variationnels, bien qu’ils ne contiennent $e$ qu’à la puissance 1 ou 0, parce qu’ils se trouvent affectés de coefficients numériques très petits.
13. Cela revient à faire abstraction, ainsi que nous l’avons déjà fait plusieurs fois, d’un même facteur constant aux seconds membres des équations (22).
14. Cf., n^o 97.
15. Peut-être qu’en ajoutant moins de foi à certains passages d’auteurs anciens qui en sont parfois peu dignes, ou dont les textes sont plus ou moins obscurs quand ils rapportent des observations d’éclipses, on arriverait à rétablir l’accord entre l’observation et la théorie de la gravitation.
16. Car on a
    $\iint \zeta \mathrm {U} _{0}\,d\sigma =0,\qquad \iint \zeta \mathrm {U} _{1}\,d\sigma =0$

    puisque $\zeta$ est une fonction sphérique du second ordre.

17. Bien entendu, nous ne conservons dans $\mathrm {W}$ que le terme le plus important, celui qui, pour les marées terrestres, est appelé terme principal semi-diurne.
18. Cette opinion, en ce qui concerne Vénus, ne paraît plus guère soutenable depuis les récentes observations spectroscopiques de M. Belopolsky.
19. H. Poincaré : Sur l’équilibre d’une masse fluide animée d’un mouvement de rotation (Acta Mathematica, t. VII, 1885, p. 250-380). Voir aussi H. Poincaré : Figures d’équilibre d’une masse fluide (Leçons professées à la Sorbonne en 1900).
20. Les points N, N₁, N₂, …, sont tous situés entre C et O.
21. Voir l’Adresse de Sir G. H. Darwin à M. H. Poincaré (Séance de la Société royale astronomique de Londres du 9 février 1900), traduite dans E. Lebon : Savants du jour : Henri Poincaré, Paris, Gauthier-Villars, 1909, p. 38-40.