Théorie mathématique de la lumière/2/Chap.06

Henri Poincaré

Théorie mathématique de la lumière

Georges Carré, 1892 (2, p. 96-122).

CHAPITRE VI

PROPAGATION RECTILIGNE DE LA LUMIÈRE

80. Étude des ondes sphériques. — Jusqu’ici nous n’avons considéré que des solutions très particulières des équations du mouvement, celles qui correspondent aux ondes planes.

Nous allons chercher à généraliser notre étude et considérer d’autres solutions de ces équations. Rappelons d’abord leur forme.

En posant :

$\theta ={\frac {d\xi }{dx}}+{\frac {d\eta }{dy}}+{\frac {d\zeta }{dz}},$

nous avons trouvé

$\rho \,{\frac {d^{2}\xi }{dt^{2}}}=\mu \left(\Delta \xi -{\frac {d\theta }{dx}}\right),\;\mathrm {etc.}$

ou

${\frac {d^{2}\xi }{dt^{2}}}=\mathrm {V} ^{2}\left(\Delta \xi -{\frac {d\theta }{dx}}\right)$

en prenant :

$\mathrm {V} ^{2}={\frac {\mu }{\rho }}\cdot$

En général nous supposerons $\theta =0$, et les équations se réduiront à

${\begin{aligned}{\frac {d^{2}\xi }{dt^{2}}}&=\mathrm {V} ^{2}\Delta \xi \\[1.25ex]{\frac {d^{2}\eta }{dt^{2}}}&=\mathrm {V} ^{2}\Delta \eta \\[1.25ex]{\frac {d^{2}\zeta }{dt^{2}}}&=\mathrm {V} ^{2}\Delta \zeta \\\end{aligned}}$

$\xi ,\,\eta ,\,\zeta$ étant de plus assujettis à la condition

$\theta =0.$

Si nous nous plaçons au point de vue de la théorie électromagnétique, nous aurons les mêmes équations pour la force magnétique $(\alpha ,\,\beta ,\,\gamma )$ et pour la force électrique $\mathrm {X,\,Y,\,Z} .$

${\begin{aligned}{\frac {d^{2}\alpha }{dt^{2}}}&=\mathrm {V} ^{2}\Delta \alpha \\[1.25ex]{\frac {d^{2}\beta }{dt^{2}}}&=\mathrm {V} ^{2}\Delta \beta \\[1.25ex]{\frac {d^{2}\gamma }{dt^{2}}}&=\mathrm {V} ^{2}\Delta \gamma ,\\\end{aligned}}$

avec

${\frac {d\alpha }{dx}}+{\frac {d\beta }{dy}}+{\frac {d\gamma }{dz}}=0$

et

${\begin{aligned}{\frac {d^{2}\mathrm {X} }{dt^{2}}}&=\mathrm {V} ^{2}\Delta \mathrm {X} \\[1.25ex]{\frac {d^{2}\mathrm {Y} }{dt^{2}}}&=\mathrm {V} ^{2}\Delta \mathrm {Y} \\[1.25ex]{\frac {d^{2}\mathrm {Z} }{dt^{2}}}&=\mathrm {V} ^{2}\Delta \mathrm {Z} ,\\\end{aligned}}$

avec

${\frac {d\mathrm {X} }{dx}}+{\frac {d\mathrm {Y} }{dy}}+{\frac {d\mathrm {Z} }{dz}}=0.$

Comme dans le premier cas, le problème se ramène à trouver trois solutions de l’équation fondamentale, ces trois solutions devant obéir à une relation différentielle.

81. Mais le problème peut se simplifier encore, car il suffit de trouver trois solutions indépendantes de l’équation pour former celles qui nous conviennent.

Soient en effet, $u,\,v,\,w,$ trois solutions indépendantes de l’équation fondamentale

(1)

${\frac {d^{2}u}{dt^{2}}}=\mathrm {V} ^{2}\Delta u,\;\mathrm {etc.}$

Faisons :

${\begin{aligned}\xi &={\frac {dw}{dy}}-{\frac {dv}{dz}}\\[1.5ex]\eta &={\frac {du}{dz}}-{\frac {dw}{dx}}\\[1.5ex]\zeta &={\frac {dv}{dx}}-{\frac {du}{dy}}\cdot \\\end{aligned}}$

$\xi ,\,\eta ,\,\zeta$ ainsi déterminés satisferont à toutes les conditions.

En effet, puisque $u,\,v,\,w$ sont des solutions de l’équation fondamentale, on a :

${\begin{aligned}{\frac {d^{2}}{dt^{2}}}\left({\frac {dw}{dy}}\right)&=\mathrm {V} ^{2}\Delta \left({\frac {dw}{dy}}\right)\\[1.5ex]{\frac {d^{2}}{dt^{2}}}\left({\frac {dv}{dz}}\right)&=\mathrm {V} ^{2}\Delta \left({\frac {dv}{dz}}\right)\cdot \\\end{aligned}}$

Retranchons la deuxième de la première, il vient :

${\frac {d^{2}\xi }{dt^{2}}}=\mathrm {V} ^{2}\Delta \xi .$

Il est facile en outre de vérifier que :

${\frac {d\xi }{dx}}+{\frac {d\eta }{dy}}+{\frac {d\zeta }{dz}}=0$

identiquement. Les fonctions $\xi ,\,\eta ,\,\zeta$ satisfont donc bien aux conditions demandées.

82. De même pour les équations de la théorie électromagnétique, il suffira de trouver trois solutions indépendantes de l’équation fondamentale ; à l’aide de celles-là, on pourra en former d’autres vérifiant l’équation de continuité.

Soient en effet $\varphi _{1},\,\varphi _{2},\,\varphi _{3},$ trois fonctions satisfaisant à l’équation :

${\frac {d^{2}\varphi }{dt^{2}}}=\mathrm {V} ^{2}\Delta \varphi .$

Posons :

${\begin{aligned}\alpha &={\frac {d^{2}\varphi _{3}}{dt\,dy}}-{\frac {d^{2}\varphi _{2}}{dt\,dz}}\\[1.5ex]\beta &={\frac {d^{2}\varphi _{1}}{dt\,dz}}-{\frac {d^{2}\varphi _{3}}{dt\,dx}}\\[1.5ex]\gamma &={\frac {d^{2}\varphi _{2}}{dt\,dx}}-{\frac {d^{2}\varphi _{1}}{dt\,dy}}\cdot \\\end{aligned}}$

On vérifierait comme dans le cas précédent que ces fonctions sont bien des solutions de l’équation fondamentale ; $\alpha ,\,\beta ,\,\gamma$ sont formés avec ${\frac {d\varphi _{1}}{dt}},\,{\frac {d\varphi _{2}}{dt}},\,{\frac {d\varphi _{3}}{dt}},$ comme $\xi ,\,\eta ,\,\zeta$ avec $u,\,v,\,w$ et ces dérivées ${\frac {d\varphi }{dt}}$ satisfont aussi à l’équation fondamentale. Il est aisé de voir aussi qu’on a identiquement

${\frac {d\alpha }{dx}}+{\frac {d\beta }{dy}}+{\frac {d\gamma }{dz}}=0.$

En ce qui concerne la force électrique, si je remplace $\alpha ,\,\beta ,\,\gamma$ par leurs expressions dans les relations

$\mathrm {K} \,{\frac {d\mathrm {X} }{dt}}={\frac {d\gamma }{dy}}-{\frac {d\beta }{dz}}$

je trouve :

$\mathrm {K} \,{\frac {d\mathrm {X} }{dt}}={\frac {d^{2}\mathrm {J} }{dt\,dx}}-\Delta {\frac {d\varphi _{1}}{dt}}$

en posant pour abréger :

$\mathrm {J} ={\frac {d\varphi _{1}}{dx}}+{\frac {d\varphi _{2}}{dy}}+{\frac {d\varphi _{3}}{dz}}\cdot$

Intégrons par rapport à $t$ en supposant que toutes les quantités soient nulles à l’origine du temps, il viendra :

${\begin{aligned}\mathrm {KX} &={\frac {d\mathrm {J} }{dx}}-\Delta \varphi _{1}\\[1.5ex]\mathrm {KY} &={\frac {d\mathrm {J} }{dy}}-\Delta \varphi _{2}\\[1.5ex]\mathrm {KZ} &={\frac {d\mathrm {J} }{dz}}-\Delta \varphi _{3}.\\\end{aligned}}$

Hertz a procédé de cette façon dans l’étude de son excitateur : il a pris :

$\varphi _{2}=\varphi _{3}=0$

et

$\varphi _{1}={\frac {\sin p\left(t-{\dfrac {r}{v}}\right)}{r}}$

$r$ étant le rayon vecteur $\textstyle {\sqrt {x^{2}+y^{2}+z^{2}}}.$ Cette fonction satisfait

à l’équation fondamentale ; elle est finie et continue en

tout point, sauf à l’origine des coordonnées.

Mais cette solution particulière ne peut pas représenter ce qui se passe dans une onde lumineuse sphérique telle que nous les observons habituellement, c’est-à-dire une onde sphérique produite par une source de dimensions infiniment petites, assimilable à un point lumineux, et étudiée en un point très éloigné de la source. Supposons l’excitateur placé à l’origine et une sphère de rayon très grand ayant son centre à l’origine : il est facile de voir que pour les points de cette sphère l’intensité est proportionnelle au carré du sinus de l’angle que fait le rayon vecteur avec $\mathrm {O} x.$ Au contraire, avec une onde lumineuse naturelle, l’intensité serait sensiblement la même dans toutes les directions.

Pour que le calcul rende compte de ce qui se passe dans le cas de l’onde lumineuse, il faut chercher une solution beaucoup plus générale que celle de Hertz.

Nous pouvons d’abord remplacer la fonction de Hertz

$\psi ={\frac {\sin p\left(t-{\dfrac {r}{v}}\right)}{r}}$

par une quelconque de ses dérivées ${\frac {d\psi }{dx}},$ ${\frac {d^{2}\psi }{dx\,dy}},$ etc., ou par une combinaison linéaire de ces dérivées. Enfin, pour avoir la solution la plus générale, il faudrait adopter pour les trois fonctions $\varphi _{1},\,\varphi _{2},\,\varphi _{3}$ des combinaisons linéaires des dérivées de tous les ordres de cete fonction $\psi .$

83. Propagation rectiligne de la lumière parallèle. — Poisson ne pouvait comprendre (cf. sa correspondance avec Fresnel) comment, dans la théorie des ondulations, il était possible que la lumière se propageât en ligne droite.

C’est ce dont nous allons essayer de nous rendre compte.

Considérons un faisceau de rayons parallèles

${\begin{aligned}\xi &=\mathrm {A} e^{{\sqrt {-1}}p\left({\frac {z}{\mathrm {V} }}-t\right)}\\[1.25ex]\eta &=\mathrm {B} e^{{\sqrt {-1}}p\left({\frac {z}{\mathrm {V} }}-t\right)}\\[1.25ex]\zeta &=\mathrm {C} e^{{\sqrt {-1}}p\left({\frac {z}{\mathrm {V} }}-t\right)}\\[1.25ex]\end{aligned}}$

$p$ est un très grand nombre ; il est égal à $2\pi$ multiplié par le nombre des oscillations par seconde ; ${\frac {p}{\mathrm {V} }}={\frac {2\pi }{\lambda }}$ est aussi un très grand nombre, $\lambda$ étant la longueur d’onde qui est très petite.

Lorsqu’il s’agit d’une onde plane, $\mathrm {A,\,B,\,C}$ sont des constantes : il n’en est plus de même ici : nous supposerons que $\mathrm {A,\,B,\,C}$ sont fonctions de $x,\,y,\,z,\,t,$ mais que ces fonctions ne varient pas très rapidement, de telle sorte qu’elles soient continues ainsi que leurs dérivées.

$\xi$ doit satisfaire à l’équation fondamentale :

${\frac {d^{2}\xi }{dt^{2}}}=\mathrm {V} ^{2}\Delta \xi .$

Or, d’après la formule de Leibnitz,

${\begin{aligned}{\frac {d^{2}\xi }{dt^{2}}}&={\frac {d^{2}\mathrm {A} }{dt^{2}}}e^{\mathrm {P} }-2{\sqrt {-1}}p\,{\frac {d\mathrm {A} }{dt}}e^{\mathrm {P} }-p^{2}\mathrm {A} e^{\mathrm {P} }\\[1.25ex]{\frac {d^{2}\xi }{dz^{2}}}&={\frac {d^{2}\mathrm {A} }{dz^{2}}}e^{\mathrm {P} }+2{\sqrt {-1}}{\frac {p}{\mathrm {V} }}{\frac {d\mathrm {A} }{dz}}e^{\mathrm {P} }-{\frac {p^{2}}{\mathrm {V} ^{2}}}\mathrm {A} e^{\mathrm {P} }\\[1.25ex]{\frac {d^{2}\xi }{dx^{2}}}&={\frac {d^{2}\mathrm {A} }{dx^{2}}}e^{\mathrm {P} }\\[1.25ex]{\frac {d^{2}\xi }{dy^{2}}}&={\frac {d^{2}\mathrm {A} }{dy^{2}}}e^{\mathrm {P} }\\\end{aligned}}$

en posant

$\mathrm {P} ={\sqrt {-1}}\,p\left({\frac {z}{\mathrm {V} }}-t\right)\cdot$

Substituons et supprimons le facteur $e^{\mathrm {P} }.$

$\mathrm {V} ^{2}\Delta \mathrm {A} +2{\sqrt {-1}}\,p\,\mathrm {V} \,{\frac {d\mathrm {A} }{dz}}-p^{2}\mathrm {A} ={\frac {d^{2}\mathrm {A} }{dt^{2}}}-2{\sqrt {-1}}\,p\,{\frac {d\mathrm {A} }{dt}}-p^{2}\mathrm {A}$

ou

(1)

$2{\sqrt {-1}}\,p\left(\mathrm {V} \,{\frac {d\mathrm {A} }{dz}}+{\frac {d\mathrm {A} }{dt}}\right)={\frac {d^{2}\mathrm {A} }{dt^{2}}}-\mathrm {V} ^{2}\Delta \mathrm {A} .$

$p$ étant très grand, nous pouvons développer $\mathrm {A}$ suivant les puissances croissantes ${\frac {1}{p}}\cdot$

$\mathrm {A} =\mathrm {A} _{0}+{\frac {\mathrm {A} _{1}}{p}}+\mathrm {{\frac {\mathrm {A} _{2}}{p^{2}}}+\cdots }$

Substituons dans l’équation et identifions les coefficients des mêmes puissances de ${\frac {1}{p}}\cdot$

${\begin{aligned}\mathrm {V} \,{\frac {d\mathrm {A} _{0}}{dz}}+{\frac {d\mathrm {A} _{0}}{dt}}&=0\\[1.5ex]2{\sqrt {-1}}\left(\mathrm {V} \,{\frac {d\mathrm {A} _{1}}{dz}}+{\frac {d\mathrm {A} _{1}}{dt}}\right)&={\frac {d^{2}\mathrm {A} _{0}}{dt^{2}}}-\mathrm {V} ^{2}\Delta \mathrm {A} _{0}\\[1.5ex]2{\sqrt {-1}}\left(\mathrm {V} \,{\frac {d\mathrm {A} _{2}}{dz}}+{\frac {d\mathrm {A} _{2}}{dt}}\right)&={\frac {d^{2}\mathrm {A} _{1}}{dt^{2}}}-\mathrm {V} ^{2}\Delta \mathrm {A} _{1}\\&\qquad \qquad \qquad \mathrm {etc.} \\\end{aligned}}$

Ces relations permettent de résoudre le problème.

En général les dérivées ${\frac {d^{2}\mathrm {A} _{0}}{dt^{2}}},\,\dots \,$ etc. seront finies, la seconde équation donnera une valeur finie pour $\mathrm {A} _{1}\,:$ ${\frac {\mathrm {A} _{1}}{p}}$ sera négligeable et il restera seulement $\mathrm {A} =\mathrm {A} _{0},$ avec

$\mathrm {V} \,{\frac {d\mathrm {A} _{0}}{dz}}+{\frac {\mathrm {d\mathrm {A} } _{0}}{dt}}=0,$

d’où :

$\mathrm {A} _{0}=f(z-\mathrm {V} t,\,x,\,y).$

Comme l’intensité est proportionnelle à $\mathrm {A} _{0}^{2},$ on voit qu’elle se propage dans la direction de $\mathrm {O} z$ avec une vitesse $\mathrm {V} ,$ ce qui explique pourquoi la lumière se propage en ligne droite.

Mais le faisceau ne pourra être aussi délié que nous le voudrons. Supposons en effet que ce faisceau soit limité par un cylindre de section très petite : $\mathrm {A}$ aurait des valeurs très grandes dans l’intérieur du cylindre et très petites à l’extérieur : il faudrait donc que $\mathrm {A}$ variât très rapidement sur les bords du faisceau. Ses dérivées deviendraient très grandes et ${\frac {\mathrm {A} _{1}}{p}}$ ne serait plus négligeable, parce que $\mathrm {A} _{1}$ deviendrait très grand : il se produirait des phénomènes de diffraction.

En raisonnant sur $\mathrm {B}$ et $\mathrm {C}$ comme nous venons de le faire sur $\mathrm {A} ,$ nous arriverions aux mêmes conclusions.

En outre, $\xi ,\,\eta ,\,\zeta$ doivent vérifier l’équation de transversalité :

${\frac {d\xi }{dx}}+{\frac {d\eta }{dy}}+{\frac {d\zeta }{dz}}=0$

qui devient, en substituant à $\xi ,\,\eta ,\,\zeta$ leurs expressions et supprimant le facteur $e^{\mathrm {P} },$

${\frac {d\mathrm {A} }{dx}}+{\frac {d\mathrm {B} }{dy}}+{\frac {d\mathrm {C} }{dz}}={\frac {{\sqrt {-1}}\,p}{\mathrm {V} }}\,\mathrm {C} .$

Développons $\mathrm {A,\,B,\,C}$ suivant les puissances croissantes de ${\frac {1}{p}}\,:$

${\begin{aligned}\mathrm {A} &=\mathrm {A} _{0}+{\frac {\mathrm {A} _{1}}{p}}+\cdots \\[1ex]\mathrm {B} &=\mathrm {B} _{0}+{\frac {\mathrm {B} _{1}}{p}}+\cdots \\[1ex]\mathrm {C} &=\mathrm {C} _{0}+{\frac {\mathrm {C} _{1}}{p}}+\cdots \\\end{aligned}}$

Faisons la substitution et égalons les coefficients des mêmes puissances de ${\frac {1}{p}}\,:$

${\frac {{\sqrt {-1}}\,\mathrm {C} _{0}}{\mathrm {V} }}=0,$

donc

$\mathrm {C} _{0}=0.$

Par conséquent $\mathrm {C}$ est très petit, de l’ordre de ${\frac {1}{p}}$ et dans une première approximation on peut prendre

$\zeta =0.$

À ce degré d’approximation, la vibration est donc parallèle au plan de l’onde

84. Réflexion totale. — J’ai supposé jusqu’ici qu’on avait affaire à une onde plane ordinaire, mais il ne sera peut-être pas sans intérêt, on verra tout à l’heure pourquoi, d’examiner ce qui se passe dans le cas des ondes planes évanescentes produites par la réflexion totale.

Si l’onde lumineuse se réfléchit (la force électrique étant perpendiculaire au plan d’incidence), nous aurons en reprenant les notations que nous avons déjà employées :

Pour l’onde incidente

$\mathrm {X} =\mathrm {A} e^{{\sqrt {-1}}(by+cz+pt)}\,;$

Pour l’onde réfléchie

$\mathrm {X} =\mathrm {B} e^{{\sqrt {-1}}(by-cz+pt)}\,;$

Et enfin pour l’onde réfractée

$\mathrm {X} =\mathrm {C} e^{{\sqrt {-1}}(by+c'z+pt)}.$

Au premier degré d’approximation, c’est-à-dire en supposant la propagation perpendiculaire à l’onde, ce qui revient à négliger les termes en ${\frac {1}{p}},$ l’équation (1) du numéro précédent deviendrait :

$\mathrm {V} \,{\frac {d\mathrm {A} }{dz}}+{\frac {d\mathrm {A} }{dt}}=0,$

puisque

$\mathrm {V} \,{\frac {d\mathrm {A} _{0}}{dz}}+{\frac {d\mathrm {A} _{0}}{dt}}=0.$

Mais dans le numéro précédent nous avions supposé l’onde parallèle au plan des $xy\,;$ nous ne faisons plus ici la même hypothèse ; on trouve alors en se bornant toujours à la première approximation :

(2)

${\begin{aligned}\mathrm {V} ^{2}\left(b\,{\frac {d\mathrm {A} }{dy}}+c\,\,{\frac {d\mathrm {A} }{dz}}\right)-p\,{\frac {d\mathrm {A} }{dt}}&=0\\[1ex]\mathrm {V} ^{2}\left(b\,{\frac {d\mathrm {B} }{dy}}-c\,\,{\frac {d\mathrm {B} }{dz}}\right)-p\,{\frac {d\mathrm {B} }{dt}}&=0\\[1ex]\mathrm {V} ^{2}\left(b\,{\frac {d\mathrm {C} }{dy}}+c'\,{\frac {d\mathrm {C} }{dz}}\right)-p\,{\frac {d\mathrm {C} }{dt}}&=0.\\\end{aligned}}$

Écrivons maintenant les conditions aux limites ; $\mathrm {X}$ et ${\frac {d\mathrm {X} }{dz}}$ doivent être continus quand on traverse la surface réfléchissante :

$\mathrm {A} +\mathrm {B} =\mathrm {C}$

(3)

$(\mathrm {A} -\mathrm {B} )c+{\frac {d\mathrm {A} }{dz}}+{\frac {d\mathrm {B} }{dz}}=\mathrm {C} c'+{\frac {d\mathrm {C} }{dz}}\cdot$

mais les dérivées par rapport à $z$ sont négligeables vis-à-vis des autres termes, et on peut écrire :

(4)

$(\mathrm {A} -\mathrm {B} )c=\mathrm {C} c'.$

Supposons qu’à l’origine nous ayons une perturbation se propageant vers la surface réfléchissante, mais circonscrite dans une certaine région, n’ayant aucun point commun avec cette surface ; nous nous donnons $\mathrm {A}$ qui est nul d’ailleurs en dehors de la région considérée ; de même $\mathrm {B}$ et $\mathrm {C}$ sont nuls. Nous pourrons calculer alors les valeurs de $\mathrm {A,\,B,\,C}$ à un instant ultérieur à l’aide des équations ci-dessus.

Si le milieu inférieur est le plus réfringent ou si le contraire ayant lieu, l’angle limite n’est pas dépassé, il n’y a rien à ajouter ; les trois équations (2) signifient que la propagation se fait perpendiculairement au plan de l’onde. Mais, s’il y a réflexion totale, $c'$ devient imaginaire. Posons :

$c'=c_{1}{\sqrt {-1}}.$

Alors :

$\mathrm {X} =\mathrm {C} e^{-c_{1}z}\cos(by+pt).$

La présence de ce cosinus a induit Cauchy en erreur. Il a conclu que ce rayon se propageait parallèlement à $\mathrm {O} y,$ c’est-à-dire à la surface réfléchissante avec une vitesse ${\frac {p}{b}}$ et il a cru observer un tel rayon dans une lunette rasant la surface réfléchissante. Mais cette observation n’a pas été vérifiée par les expériences ultérieures, en particulier par les expériences que M. Quincke a faites sur les anneaux colorés. Nous avons vu qu’en faisant tomber de la lumière sur la base d’un prisme à réflexion totale, au point de contact de cette base avec une lentille, on observait des anneaux ou plutôt une tache lumineuse. Si le rayon tombe en dehors du point de contact et que le rayon réfracté se propage parallèlement à la surface comme le veut Cauchy, on observera encore des anneaux : or rien de pareil n’a été observé. Il est aisé de le comprendre.

Les équations (2) sont encore les mêmes pour les ondes imaginaires, mais elles ne doivent plus recevoir la même interprétation. Les deux premières montrent encore que le rayon se propage perpendiculairement au plan d’onde, mais la dernière n’a plus la même signification quand on y fait $c'$ imaginaire.

Les équations (3) et (4) nous apprennent d’abord quelles sont les valeurs de $\mathrm {A,\,B,\,C}$ sur la surface réfléchissante, et en particulier que ces valeurs sont nulles en dehors des parties de cette surface où tombent les rayons incidents.

La troisième équation (2) nous permettrait ensuite de calculer $\mathrm {C}$ en un point situé à distance finie de cette surface ; mais cela est inutile ; en un pareil point, en effet, quel que soit $\mathrm {C} ,$ $\mathrm {X}$ sera négligeable à cause du facteur $e^{-c_{1}z}$ qui est très petit dès que $z$ atteint une valeur notable. Ainsi pas de lumière près de la surface réfléchissante en dehors des points où tombent les rayons incidents à cause des équations (3) et (4) ; pas de lumière non plus loin de cette surface à cause de ce facteur exponentiel.

85. Étude des faisceaux très déliés. — Il est possible de nous représenter d’une manière un peu plus précise le degré de ténuité que peut prendre le faisceau lumineux sans que les lois de la propagation soient changées. Considérons la fonction de Bessel

$\mathrm {J} _{0}(x)=1-{\frac {x^{2}}{2^{2}}}+{\frac {x^{4}}{2^{2}.4^{2}}}-{\frac {x^{6}}{2^{2}.4^{2}.6^{2}}}+\cdots$

Cette série est convergente quel que soit $x,$ et il est aisé de vérifier qu’elle satisfait à la relation :

${\frac {d^{2}\mathrm {J} _{0}}{dx^{2}}}+{\frac {1}{x}}{\frac {d\mathrm {J} _{0}}{dx}}+\mathrm {J} _{0}=0.$

Si nous construisons la courbe

$y=\mathrm {J} _{0}(x),$

Fig. 11.

cette courbe sera symétrique par rapport à l’axe des $y$ ; elle coupe cet axe au point $y=1,$, et présente ensuite des ordonnées maxima et minima qui vont en décroissant à mesure que $x$ devient plus grand (fig. 11).

Pour $x$ suffisamment grand, $\mathrm {J} _{0}$ est représenté asymptotiquement par

$\mathrm {J} _{0}=\cos \left(x-{\frac {\pi }{4}}\right){\sqrt {\frac {2}{\pi x}}}$

À partir d’un certain moment, $\mathrm {J} _{0}$ est donc $<{\sqrt {\frac {2}{\pi x}}}\cdot$ Ainsi pour $x>64,$ $\mathrm {J} _{0}$ est toujours plus petit que ${\frac {1}{10}}\cdot$

Reprenons l’équation fondamentale

${\frac {d^{2}\xi }{dt^{2}}}=\mathrm {V} ^{2}\Delta \xi .$

Supposons en particulier que $\xi$ soit une fonction de $z,$ de $t$ et de $\rho ={\sqrt {x^{2}+y^{2}}},$ autrement dit que $\xi$ ne change pas quand les axes tournent d’un angle quelconque autour de $\mathrm {O} z.$ L’équation prend alors la forme :

${\frac {1}{\mathrm {V} ^{2}}}{\frac {d^{2}\xi }{dt^{2}}}={\frac {d^{2}\xi }{d\rho ^{2}}}+{\frac {1}{\rho }}{\frac {d\xi }{d\rho }}+{\frac {d^{2}\xi }{dz^{2}}}\cdot$

Posons :

$\xi =\mathrm {A} \,\mathrm {J} _{0}(h\rho )\,\cos 2\pi \left({\frac {z}{l}}-{\frac {t}{\mathrm {T} }}\right)\cdot$

$\mathrm {A} ,\,h,\,l,\,\mathrm {T}$ étant des constantes.

$\mathrm {T}$ est la période, $l$ une quantité analogue à la longueur d’onde $\lambda =\mathrm {VT} .$ Nous pourrons appeler $l$ longueur d’onde apparente par opposition à la longueur d’onde normale $\lambda .$

Pour que $\xi$ satisfasse à l’équation fondamentale, il faut que ces quatre constantes soient liées par une relation. En effet :

${\frac {d^{2}\xi }{d\rho ^{2}}}+{\frac {1}{\rho }}{\frac {d\xi }{d\rho }}+h^{2}\xi =0,$

puisque seul le facteur $\mathrm {J} _{0}(h\rho )$ dépend de $\rho .$

${\begin{aligned}{\frac {d^{2}\xi }{dz^{2}}}&=-{\frac {4\pi ^{2}}{l^{2}}}\xi \\[1ex]{\frac {d^{2}\xi }{dt^{2}}}&=-{\frac {4\pi ^{2}}{\mathrm {T} ^{2}}}\xi .\\\end{aligned}}$

Substituons ces valeurs dans l’équation et nous obtenons la condition :

${\frac {h^{2}}{4\pi ^{2}}}={\frac {1}{\mathrm {V} ^{2}\mathrm {T} ^{2}}}-{\frac {1}{l^{2}}}={\frac {1}{\lambda ^{2}}}-{\frac {1}{l^{2}}}\cdot$

Cette formule nous apprend que $l$ n’est pas égal à $\lambda ,$ mais que $l>\lambda .$

Mais nous ne pourrons pas supposer que cette différence $l-\lambda$ soit grande, car les phénomènes différeraient trop alors des phénomènes lumineux pour qu’il nous soit permis d’appliquer nos équations à ces derniers. La valeur de $l-\lambda$ nous donnera donc en quelque sorte une mesure de la finesse que peut prendre un faisceau lumineux, sans que les lois de la propagation soient troublées.

Pour plus de clarté, prenons quelques nombres. Posons par exemple :

$\rho ={\frac {64}{h}}\qquad$ ou $\qquad \mathrm {J} _{0}(h\rho )=\mathrm {J} _{0}(64).$

D'après ce que nous avons vu, on a :

$\mathrm {J} _{0}(64)<{\frac {1}{10}}\cdot$

L’intensité lumineuse est proportionnelle à $\mathrm {J} _{0}^{2},$ c’est-à-dire qu’elle sera plus petite que le ${\frac {1}{100}}$ de l’intensité en un point de $\mathrm {O} z,$ dès que l’on sera à une distance de cet axe égale ou supérieure à ${\frac {64}{h}}\cdot$

Si nous considérons par exemple un cylindre de révolution autour de $\mathrm {O} z$ et de rayon égal à

$\rho _{0}=64\,$ µ

et que nous prenions $\lambda ={\frac {1}{2}}\,\mu ,$ nous trouverons que l’erreur relative ${\frac {l-\lambda }{\lambda }}$ est inférieure à ${\frac {1}{300}}\cdot$

Avec $\rho _{0}=640$ µ, c’est-à-dire un diamètre de un peu plus de $1$ millimètre, cette erreur devient inférieure à ${\frac {1}{30000}}\cdot$

86. On serait tenté de croire, d’après ce qui précède, que la vitesse de propagation d’un faisceau très délié est égale à ${\frac {l}{\mathrm {T} }}$ et par conséquent plus grande que la vitesse normale. Ce serait une erreur.

Reprenons en effet la formule

$\xi =\mathrm {A} \mathrm {J} _{0}(h\rho )\,\cos 2\pi \left({\frac {z}{l}}-{\frac {t}{\mathrm {T} }}\right),$

et posons pour abréger

$\varphi =\mathrm {J} _{0}(h\rho )\cos 2\pi \left({\frac {z}{l}}-{\frac {t}{\mathrm {T} }}\right)\cdot$

Jusqu’ici $\mathrm {A}$ était considéré comme une constante : nous le regarderons maintenant comme une fonction de $z$ et de $t.$

Substituons à $\xi$ son expression dans l’équation

${\frac {1}{\mathrm {V} ^{2}}}{\frac {d^{2}\xi }{dt^{2}}}=\Delta \xi .$

On a :

${\begin{aligned}{\frac {d^{2}\xi }{dz^{2}}}&={\frac {d^{2}\mathrm {A} }{dz^{2}}}\varphi +2{\frac {d\mathrm {A} }{dz}}{\frac {d\varphi }{dz}}+\mathrm {A} {\frac {d^{2}\varphi }{dz^{2}}}\\[1ex]{\frac {d^{2}\xi }{dx^{2}}}&=\mathrm {A} {\frac {d^{2}\varphi }{dx^{2}}}\\[1ex]{\frac {d^{2}\xi }{dy^{2}}}&=\mathrm {A} {\frac {d^{2}\varphi }{dy^{2}}}\\\end{aligned}}$

${\frac {1}{\mathrm {V} ^{2}}}\left({\frac {d^{2}\mathrm {A} }{dt^{2}}}\varphi +2{\frac {d\mathrm {A} }{dt}}{\frac {d\varphi }{dt}}+\mathrm {A} {\frac {d^{2}\varphi }{dt^{2}}}\right)={\frac {1}{\mathrm {V} ^{2}}}{\frac {d^{2}\xi }{dt^{2}}}$

$\mathrm {A} \Delta \varphi ={\frac {\mathrm {A} }{\mathrm {V} ^{2}}}{\frac {d^{2}\varphi }{dt^{2}}}\cdot$

Additionnons ces sept relations membre à membre et faisons les réductions ; il vient :

${\frac {1}{\mathrm {V} ^{2}}}\left[{\frac {d^{2}\mathrm {A} }{dt^{2}}}\varphi +2{\frac {d\mathrm {A} }{dt}}{\frac {d\varphi }{dt}}\right]={\frac {d^{2}\mathrm {A} }{dz^{2}}}\varphi +2{\frac {d\mathrm {A} }{dz}}{\frac {d\varphi }{dz}}\cdot$

D’autre part :

${\begin{aligned}{\frac {d\varphi }{dt}}&=\;\mathrm {J} _{0}(h\rho )\,{\frac {2\pi }{\mathrm {T} }}\sin 2\pi \left({\frac {z}{l}}-{\frac {t}{\mathrm {T} }}\right)\\[1.5ex]{\frac {d\varphi }{dz}}&=-\mathrm {J} _{0}(h\rho )\,{\frac {2\pi }{l}}\sin 2\pi \left({\frac {z}{l}}-{\frac {t}{\mathrm {T} }}\right)\cdot \\\end{aligned}}$

Or ${\frac {2\pi }{\mathrm {T} }}$ et ${\frac {2\pi }{l}}$ sont des nombres très grands, les autres facteurs sont de l’ordre de $\varphi \,:$ ${\frac {d\varphi }{dt}}$ et ${\frac {d\varphi }{dz}}$ sont donc très grands vis-à-vis de $\varphi$ et les termes qui contiennent seulement $\varphi$ peuvent être négligés en regard de ceux qui contiennent ces dérivées.

Notre relation se réduira donc à :

${\frac {1}{\mathrm {V} ^{2}}}{\frac {d\mathrm {A} }{dt}}{\frac {d\varphi }{dt}}={\frac {d\mathrm {A} }{dz}}{\frac {d\varphi }{dz}}\cdot$

Substituons aux dérivées leurs valeurs ; nous trouvons :

$l\,{\frac {d\varphi }{dz}}+\mathrm {T} \,{\frac {d\varphi }{dt}}=0,$

et par suite :

$-{\frac {l}{\mathrm {V} ^{2}}}{\frac {d\mathrm {A} }{dt}}=\mathrm {T} \,{\frac {d\mathrm {A} }{dz}},$

ou

${\frac {d\mathrm {A} }{dt}}+{\frac {\mathrm {V} ^{2}\mathrm {T} }{l}}{\frac {d\mathrm {A} }{dz}}=0.$

L’intégrale générale de cette équation est la suivante :

$\mathrm {A} =f\left(z-{\frac {\mathrm {V} ^{2}\mathrm {T} }{l}}\,t\right)\cdot$

La perturbation se propage donc avec une vitesse ${\frac {\mathrm {V} ^{2}\mathrm {T} }{l}}=\mathrm {V} {\frac {\lambda }{l}}\cdot$ Cette vitesse est donc moindre que la vitesse normale. Cette différence n’a jamais été observée, ce qui prouve que $l-\lambda$ est toujours négligeable.

87. Propagation de la lumière non parallèle. — Pour étudier ce qui se passe dans le cas où le faisceau est formé de rayons qui ne sont pas parallèles, nous ferons un changement de coordonnées.

Considérons trois fonctions $u,\,v,\,w$ de $x,\,y,\,z$ et les trois systèmes de surfaces :

$u=\mathrm {C^{te}} ,\quad v=\mathrm {C^{te}} ,\quad w=\mathrm {C^{te}} .$

Nous prendrons comme nouvelles coordonnées $u,\,v,\,w,$ et nous supposerons que les surfaces forment un système triple orthogonal.

Considérons deux points dont les coordonnées soient $(u,v,w),$ $(u+du,\,v,\,w),$ autrement dit deux points infiniment voisins situés sur une normale à la surface $u=\mathrm {C^{te}} \,;$ j’appellerai $a\,du$ la distance de ces deux points. De même $b\,dv$ sera la distance de deux points $(u,v,w),$ $(u,\,v+dv,\,w),$ infiniment voisins situés sur une normale à la surface $v=\mathrm {C^{te}} \,;$ $c\,dw,$ la distance des deux points $(u,v,w),$ $(u,\,v,\,w+dw)\dots$ etc., $a,\,b,\,c$ étant des fonctions de $(x,y,z).$

On démontre alors que :

$abc\,\Delta \xi ={\frac {d}{du}}\left({\frac {bc}{a}}{\frac {d\xi }{du}}\right)+{\frac {d}{dv}}\left({\frac {ca}{b}}{\frac {d\xi }{dv}}\right)+{\frac {d}{dw}}\left({\frac {ab}{c}}{\frac {d\xi }{dw}}\right)\cdot$

Et l’équation

${\frac {1}{\mathrm {V} ^{2}}}{\frac {d^{2}\xi }{dt^{2}}}=\Delta \xi$

devient dans ce nouveau système

${\frac {abc}{\mathrm {V} ^{2}}}{\frac {d^{2}\xi }{dt^{2}}}={\frac {d}{du}}\left({\frac {bc}{a}}{\frac {d\xi }{du}}\right)+\cdots$

Nous ferons en outre sur les systèmes de surfaces une hypothèse particulière. Les surfaces $w=\mathrm {C^{te}}$ seront des surfaces parallèles : les trajectoires orthogonales

$\left\{{\begin{aligned}u=\mathrm {C^{te}} \\v=\mathrm {C^{te}} \\\end{aligned}}\right.$

seront les normales communes à ces surfaces ; $w$ sera une longueur
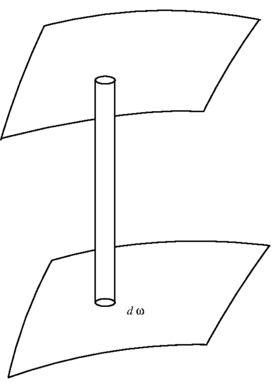
Fig. 12. comptée sur ces normales, la distance des deux points $(u,\,v,\,w)$, $(u,\,v,\,w+dw)$ sera $dw$ et par suite $c=1.$

Considérons deux des surfaces $w,$ prenons sur la première un élément d’aire $d\omega '$ infiniment petit et menons les normales en tous les points de son contour : le pinceau de normales ainsi obtenu découpera sur l’autre surface un élément d’aire $d\omega ''$ (fig. 12).

Soient $a'$ et $b'$ les valeurs des coefficients $a$ et $b$ relatives à $d\omega ',$ $a''$ et $b''$ les valeurs relatives à $d\omega ''.$

Nous aurons

${\frac {d\omega '}{a'b'}}={\frac {d\omega ''}{a''b''}}\cdot$

Si donc nous posons :

$abc={\frac {ab}{c}}=s,$

$s$ sera aux différents points d’un même pinceau de normales infiniment délié proportionnel à la section droite de ce pinceau.

Soit :

$\xi =\mathrm {A} \cos p(w-\mathrm {V} t),$

$p$ étant un très grand nombre (comme ci-dessus). $\mathrm {A}$ est une fonction quelconque de $(u,\,v,\,w).$ Je suppose que ces dérivées sont finies, ce qui sera vrai en tous les points du faisceau, sauf en général sur les bords.

Il résultera de cette hypothèse que les termes seront de grandeur très différente suivant qu’ils contiendront en facteur $p,\,p^{2}\dots$ ou ne contiendront pas $p.$ Aussi ne conserverons-nous que les termes renfermant au moins $p$ en facteur.

Alors les termes

${\begin{aligned}{\frac {d}{du}}\left({\frac {bc}{a}}\,{\frac {d\xi }{du}}\right)&=\cos p(w-\mathrm {V} t)\left({\frac {d}{du}}\,{\frac {bc}{a}}\,{\frac {d\mathrm {A} }{du}}\right),\\[1.5ex]{\frac {d}{dv}}\left({\frac {ca}{b}}\,{\frac {d\xi }{dv}}\right)&=\cos p(w-\mathrm {V} t)\left({\frac {d}{dv}}\,{\frac {ca}{b}}\,{\frac {d\mathrm {A} }{dv}}\right)\\\end{aligned}}$

seront négligeables.

Posons pour abréger

$p(w-\mathrm {V} t)=\omega ,$

il vient :

${\begin{aligned}{\frac {abc}{\mathrm {V} ^{2}}}{\frac {d^{2}\xi }{dt^{2}}}&={\frac {s}{\mathrm {V} ^{2}}}\left({\frac {d^{2}\mathrm {A} }{dt^{2}}}\cos \omega +2\,{\frac {d\mathrm {A} }{dt}}\,p\mathrm {V} \sin \omega -p^{2}\mathrm {V} ^{2}\mathrm {A} \cos \omega \right)\\[1.5ex]{\frac {d\xi }{dw}}&={\frac {d\mathrm {A} }{dw}}\cos \omega -p\,\mathrm {A} \,\sin \omega \\[1.5ex]s\,{\frac {d\xi }{dw}}&=s\,{\frac {d\mathrm {A} }{dw}}\cos \omega -ps\mathrm {A} \,\sin \omega \\[1.5ex]{\frac {d}{dw}}\left(s\,{\frac {d\xi }{dw}}\right)&={\frac {d}{dw}}\left(s\,{\frac {d\mathrm {A} }{dw}}\right)\cos \omega -ps\,{\frac {d\mathrm {A} }{dw}}\sin \omega -p\mathrm {A} \,{\frac {ds}{dw}}\sin \omega \\&\qquad -ps\,{\frac {d\mathrm {A} }{dw}}\sin \omega -p^{2}\mathrm {A} s\cos \omega .\\\end{aligned}}$

Le premier terme ne contenant pas $p$ est négligeable, il reste :

${\frac {d}{dw}}\left(s\,{\frac {d\xi }{dw}}\right)=-p\,\sin \omega \left({\frac {2s\,d\mathrm {A} +\mathrm {A} \,ds}{dw}}\right)-p^{2}\mathrm {A} s\cos \omega .$

L’équation fondamentale devient donc : en remarquant que les termes en $p^{2}$ se détruisent et supprimant les facteurs communs :

${\frac {1}{\mathrm {V} }}\,s\,{\frac {d\mathrm {A} }{dt}}=-s\,{\frac {d\mathrm {A} }{dw}}-{\frac {1}{2}}\,\mathrm {A} \,{\frac {ds}{dw}}$

ou

${\frac {\sqrt {s}}{\mathrm {V} }}{\frac {d\mathrm {A} }{dt}}=-{\sqrt {s}}\,{\frac {d\mathrm {A} }{dw}}-\mathrm {A} \,{\frac {d{\sqrt {s}}}{dw}}$

comme $s$ est indépendant de $t$

${\frac {1}{\mathrm {V} }}\,{\frac {d\mathrm {A} {\sqrt {s}}}{dt}}=-{\frac {d\mathrm {A} {\sqrt {s}}}{dw}}\cdot$

Intégrons

${\begin{aligned}&\mathrm {A} {\sqrt {s}}=f(u,\,v,\,w-\mathrm {V} t),\\[1ex]&\mathrm {A} ={\frac {1}{\sqrt {s}}}f(u,\,v,\,w-\mathrm {V} t).\\\end{aligned}}$

La perturbation se propage donc avec une vitesse $\mathrm {V}$ rectiligne dans la direction des normales

$\left\{{\begin{aligned}u=\mathrm {C^{te}} \\v=\mathrm {C^{te}} \\\end{aligned}}\right.$

aux surfaces parallèles $w=\mathrm {C^{te}} .$

L’amplitude varie comme ${\frac {1}{\sqrt {s}}}$ et par suite l’intensité est proportionnelle à ${\frac {1}{s}}\,;$ c’est-à-dire qu’elle est en raison inverse de la section du faisceau.

Il est à remarquer que cette formule contient toute l’optique géométrique.

88. Les surfaces $w=\mathrm {C^{te}}$ sont les surfaces de l’onde. Comme cas particulier on peut supposer que ce sont des sphères, les rayons lumineux se réduisent alors aux rayons de la sphère.

L’intensité est proportionnelle à ${\frac {1}{s}}\,:$ mais dans le calcul actuel

${\frac {d\omega }{r^{2}}}={\frac {d\omega '}{r'^{2}}},$

donc

$s=r^{2}$

et

$\mathrm {A} ={\frac {1}{2}}f(\varphi ,\,\theta ,\,r-\mathrm {V} t),$

$\varphi ,\,\theta ,\,r$ étant les coordonnées polaires définies par les relations :

${\begin{aligned}x&=r\cos \varphi \cos \theta \\[1ex]y&=r\sin \varphi \cos \theta \\[1ex]z&=r\sin \theta .\\\end{aligned}}$

Nous avons à tenir compte encore de la condition de transversalité. Soient :

${\begin{alignedat}{2}\xi &=\mathrm {A} \cos p(r-\mathrm {V} t)&&=\mathrm {A} \cos \omega \\[1ex]\eta &=\mathrm {B} \cos p(r-\mathrm {V} t)&&=\mathrm {B} \cos \omega \\[1ex]\zeta &=\mathrm {C} \cos p(r-\mathrm {V} t)&&=\mathrm {C} \cos \omega .\\\end{alignedat}}$

Les fonctions $\mathrm {A,\,B,\,C}$ ne sont pas indépendantes, mais elles sont liées par une relation que nous obtiendrons précisément en écrivant la condition de transversalité

${\frac {d\xi }{dx}}+{\frac {d\eta }{dy}}+{\frac {d\zeta }{dz}}=0.$

Or

${\frac {d\xi }{dx}}={\frac {d\mathrm {A} }{dx}}\,\cos \omega -\mathrm {A} \,\sin \omega \,{\frac {d\omega }{dr}}{\frac {dr}{dx}}={\frac {d\mathrm {A} }{dx}}\,\cos \omega -p\mathrm {A} \,\sin \omega \,{\frac {x}{r}}\cdot$

Le premier terme ne contient pas $p$ et est négligeable. Donc :

${\begin{aligned}{\frac {d\xi }{dx}}&=-{\frac {p}{r}}\mathrm {A} x\sin \omega ,\\[1.5ex]{\frac {d\eta }{dy}}&=-{\frac {p}{r}}\mathrm {B} y\sin \omega ,\\[1.5ex]{\frac {d\zeta }{dz}}&=-{\frac {p}{r}}\mathrm {C} z\sin \omega .\\\end{aligned}}$

La condition de transversalité s’écrira :

$\mathrm {A} x+\mathrm {B} y+\mathrm {C} z=0.$

D’ailleurs

$x^{2}+y^{2}+z^{2}=r^{2}.$

Si trois fonctions réelles$\mathrm {A,\,B,\,C}$ des coordonnées d’un point de la sphère satisfont à cette relation, il y a forcément sur la sphère deux points au moins pour lesquels simultanément $\mathrm {A} =0,$ $\mathrm {B} =0,$ $\mathrm {C} =0,$ et pour lesquels par conséquent l’intensité lumineuse serait nulle. En effet, entre les deux relations :

${\begin{alignedat}{3}\mathrm {A} \,dx&+\mathrm {B} \,dy&&+\mathrm {C} \,dz&&=0\\x\,dx&+y\,dy&&+z\,dz&&=0\\\end{alignedat}}$

on peut éliminer $dz$ par exemple et obtenir une équation différentielle ordinaire. Cette équation représentera certaines courbes tracées sur la sphère, ces courbes auront des points singuliers pour lesquels $\mathrm {A=B=C=} 0\,;$ (cf. mon Mémoire sur les courbes définies par les équations différentielles, Journal de Liouville, 3^e série, tome vii).

En effet, on démontre que de semblables courbes ont des points singuliers de deux espèces et que le nombre des points singuliers de première espèce surpasse toujours de deux unités celui des points de deuxième espèce. Il y aura donc toujours sur la sphère au moins deux points singuliers pour ces courbes.

Mais alors dans cette direction, $\mathrm {A,\,B,\,C}$ étant nuls, l’intensité lumineuse sera nulle. Or l’expérience montre que l’onde sphérique n’est pas ainsi constituée et que l’intensité est la même dans toutes les directions. Mais ceci n’infirme pas la théorie : en effet, les coefficients $\mathrm {A,\,B,\,C}$ sont variables ; par exemple $\mathrm {A}$ est une fonction de $\omega ,$ de $\theta ,$ de $r-\mathrm {V} t.$ Si nous considérons un point sur une sphère donnée, dans une direction donnée, $\omega ,\,\theta ,\,r$ ont des valeurs déterminées, mais $\mathrm {A}$ varie avec $t.$ Cette variation des coefficients $\mathrm {A,\,B,\,C}$ est très lente relativement à la durée des vibrations, mais très rapide relativement à nos unités ordinaires par exemple à la durée (¹/₁₀ de seconde) de la persistance des impressions lumineuses sur la rétine : dans cet intervalle, $\mathrm {A,\,B,\,C}$ ont pris un grand nombre de fois toutes les valeurs dont ils sont susceptibles, et on n’observe que l’intensité moyenne. Il convient d’ajouter que la phase ne sera pas la même dans toutes les directions et par conséquent que $\mathrm {A,\,B,\,C}$ seront imaginaires ; il y aura alors une direction pour laquelle les parties réelles de $\mathrm {A,\,B,\,C}$ s’annuleront à le fois, et une autre pour laquelle les parties imaginaires seront nulles à la fois ; mais ces deux directions ne coïncideront pas, de sorte qu’il n’y aura pas de direction d’intensité nulle ; mais cette circonstance ne suffirait pas à elle seule pour expliquer l’égalité d’intensité dans toutes les directions.

---