Des théorèmes mécaniques (trad. Reinach)/Théorème III
(Théorème III)[1].
1o Le cylindre ayant une base égale au plus grand cercle d’un ellipsoïde de révolution[2] et une hauteur égale à l’axe de ce solide vaut les 3/2 de l’ellipsoïde.
2o Quand on coupe un ellipsoïde par un plan passant par son centre et perpendiculaire à son axe, le demi-ellipsoïde ainsi déterminé est double du cône ayant même base et même axe.
Soit l’ellipsoïde K (fig. 4) coupé par un plan 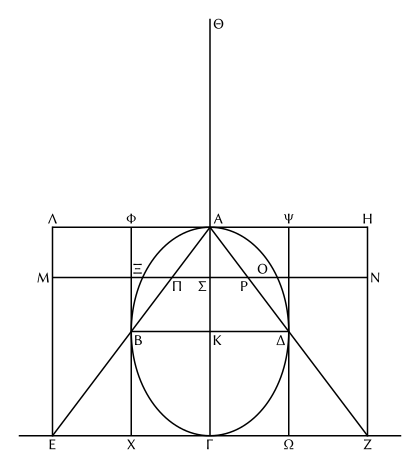
Fig. 4. passant par son axe suivant l’ellipse[3] ΑΒΓΔ, les diamètres ΑΓ, ΒΔ, le centre K ; soit encore le grand cercle de diamètre ΒΔ perpendiculaire à ΑΓ.
Considérons le cône ayant pour base le cercle ΒΔ, pour sommet Α, et prolongeons la surface latérale jusqu’à son intersection, suivant le cercle ΕΖ, avec le plan mené par Γ parallèlement à la base ; construisons aussi le cylindre ayant pour base le cercle ΕΖ, pour axe ΑΓ ; enfin prolongeons ΑΓ d’une longueur égale ΑΘ, et considérons ΘΓ comme un levier ayant Α pour milieu fixe.
Dans le rectangle ΛΖ, menons à ΕΖ une parallèle quelconque ΜΝ, et par ΜΝ un plan perpendiculaire à l’axe ΑΓ. Ce plan coupera le cylindre suivant un cercle de diamètre ΜΝ, l’ellipsoïde suivant un cercle de diamètre ΞΟ, le cône suivant un cercle de diamètre ΠΡ.
On a :
(1) |
ΑΓΑΣ = ΑΕΑΠ = ΜΣΣΠ, |
donc aussi :
(2) |
ΑΘΑΣ = ΜΣΣΠ = ΜΣ²ΜΣ × ΣΠ. |
Je dis maintenant que ΜΣ × ΣΠ = ΣΠ² + ΣΞ². En effet, on a :
(3) |
ΑΣ × ΣΓΣΞ² = ΑΚ × ΚΓΚΒ², |
car l’un et l’autre rapport égale celui du grand axe au paramètre[4].
Dès lors (puisque ΑΚ = ΚΓ) :
intervertissant :
Mais (à cause de ΑΣΣΓ = ΣΠΠΜ) :
Donc :
c’est-à-dire :
Ajoutant de part et d’autre ΣΠ², il vient :
comme nous l’avions annoncé.
Remplaçons maintenant, dans l’égalité (2), ΜΣ × ΣΠ par sa valeur ; il vient :
En d’autres termes, par rapport au point fixe Α, le cercle ΜΝ, restant en place, équilibrera la somme des cercles ΟΞ et ΠΡ suspendus au centre de gravité commun Θ, car les distances des centres de gravité au point fixe sont inversement proportionnelles aux poids considérés.
Semblablement, pour toute parallèle à ΕΖ menée à l’intérieur du rectangle ΑΖ et par laquelle on mène un plan perpendiculaire à ΑΓ, le cercle intercepté dans le grand cylindre, restant en place, équilibrera par rapport à Α les deux cercles interceptés dans l’ellipsoïde et dans le cône, transférés en Θ, comme centre de gravité commun.
Remplissons complètement ces trois corps de cercles semblables. Au total, le cylindre restant en place équilibrera l’ellipsoïde et le cône ΑΕΖ transportés en Θ. Le cylindre a pour centre de gravité Κ, on doit donc avoir :
Mais ΘΑ = 2ΑΚ, donc :
Mais le cylindre ΛΖ vaut trois fois le cône ΑΕΖ qui a même base et même hauteur ; donc :
ou
Le cône ΑΕΖ vaut huit fois le cône ΑΒΔ dont le rayon de base et l’axe sont moitié des siens, donc :
et
Menons maintenant dans le rectangle ΛΖ les parallèles ΧΦ, ΩΨ à l’axe par les points Β, Δ et considérons le cylindre ΦΨΩΧ. Il est évidemment double du cylindre ΦΨΔΒ, qui a base égale et axe moitié moindre ; ce dernier vaut trois fois le cône ΑΒΔ, donc :
et comme le cône vaut le quart de l’ellipsoïde :
- ↑ Cf. De conoid., prop. 29-30.
- ↑ Archimède dit : « un sphéroïde ».
- ↑ Archimède dit : « une section de cône acutangle ».
- ↑ τῷ τῆς πλαγίας πρὸς τὴν ὀρθίαν. La πλαγία (d’une ellipse) est le grand axe (ou diamètre par excellence). L’ὀρθία ou paramètre est une longueur dont la mesure est déterminée par Apollonius, Coniques, I, 13. Étant donnée une ellipse dans un cône (fig. 5), il mène, par le sommet Α du cône, une parallèle au grand axe ΕΔ de l’ellipse jusqu’à sa rencontre Κ avec un diamètre ΒΓ de la base du cône. Il prend ensuite la perpendiculaire ΕΘ à ΕΔ telle que :
ΕΘΕΔ = ΒΚ.ΚΓΑΚ².
ΕΘ sera le paramètre (ὁρθία). Apollonius démontre (I, 21 ; p. 75, Heib.) que, pour un point Ξ quelconque de l’ellipse, on a :
ΞΣ²ΑΣ × ΣΓ = paramètregrand axe.Heiberg croit que les mots soulignés au texte ont été interpolés
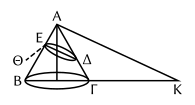
Fig. 5. ou du moins substitués à une phrase autrement rédigée, parce que les termes ὀρθία et πλαγία sont de la création d’Apollonius.L’égalité (3) peut d’ailleurs être démontrée assez simplement en considérant l’ellipse comme la projection orthogonale d’un cercle (théorème de Stevin). Soient 2a, 2b les axes de l’ellipse, y, y′ deux ordonnées quelconques correspondantes du cercle et de l’ellipse. On a évidemment dans le cercle : y² = ΑΣ.ΣΓ et, comme y′ = y ba, il vient : y′² = (ΑΣ.ΣΓ) b²a² d’où ΑΣ.ΣΓy′² = a²b² = constante.
On peut aussi déduire cette relation de l’équation de l’ellipse rapportée à ses axes x²a² + y²b² = 1, d’où y² = (a² − x²) b²a². Or, ΑΣ.ΣΓy² = (a + x) (a − x)y² = a² − x²y² = a²b² = constante.

