L’Emploi des mathématiques en économie politique/II

Jacques Moret

L’Emploi des mathématiques en économie politique

M. Giard & É. Brière, 1915 (p. 61-156).

DEUXIÈME PARTIE

Historique de l’emploi des mathématiques en économie politique.

À proprement parler, ce n’est pas tant l’historique de l’emploi des mathématiques en économie politique que l’histoire des économistes qui ont fait appel aux mathématiques que nous allons essayer d’esquisser ici. Étant donné en effet, d’après ce que nous avons vu, qu’il n’existe pas d’école mathématique, c’est-à-dire que l’emploi bien entendu des mathématiques en économie politique n’a pas pour but l’élaboration d’un corps de doctrines particulières dont on puisse suivre la genèse, mais uniquement l’explication scientifique de questions de fait, il ne nous paraît guère possible d’adopter dans cette partie de notre travail un ordre autre que celui qui nous est naturellement fourni par la succession chronologique des auteurs d’œuvres mathématico-économiques. Par suite, nous nous proposons de passer rapidement en revue ces auteurs, en nous efforçant de mettre en évidence les caractères de similitude ou même de dissemblance qui, en les rattachant les uns aux autres, constituent les seuls éléments anonymes dont l’évolution puisse être considérée comme l’histoire de l’emploi des mathématiques en économie politique.

Mais nous ne songeons cependant nullement à nous arrêter à tous les auteurs d’œuvres mathématico-économiques, car, en présence de l’abondance de ces productions, nous serions amenés à entrer dans des développements absolument hors de proportion et avec un examen d’ensemble tel que celui que nous avons entrepris, et avec l’intérêt même qu’ils seraient susceptibles d’offrir ; nous avons simplement l’intention de présenter uniquement ceux d’entre ces auteurs dont les œuvres nous semblent les plus importantes, eu égard aux époques où elles où été écrites. Après avoir signalé tous ceux qui dans les débuts ont appliqué les mathématiques au traitement de questions économiques même très particulières, nous laisserons peu à peu de côté les auteurs d’études trop spéciales, dont la seule mention dans les bibliographies dont nous indiquerons ultérieurement l’existence paraît suffisante, pour ne nous occuper, dans la période contemporaine, que des économistes ayant apporté une réelle contribution à l’édification des seules théories qui justifient pleinement l’emploi des mathématiques.

Nous allons donc tout d’abord rappeler les noms des précurseurs, qui, s’ils n’ont guère participé à l’élaboration des conceptions modernes, ont du moins contribué à leur formation, tant en fournissant l’idée de l’emploi des mathématiques en économie politique qu’en indiquant les premiers éléments de cet emploi. Puis, nous nous arrêterons plus longuement sur les fondateurs de l’économie pure, qui, par la découverte du principe de l’utilité finale et son application à la détermination des prix sous le régime de la libre concurrence, ont été conduits à faire, pour la première fois, une application rationnelle importante des mathématiques en les utilisant pour représenter la solidarité des transactions qui s’effectuent sur un marché. Nous parlerons enfin des économistes contemporains qui ont perfectionné l’emploi des mathématiques en économie politique en le dégageant tout d’abord de l’hypothèse de la possibilité de mesurer l’utilité, possibilité primitivement considérée comme nécessairement liée à l’application du principe de l’utilité finale qui avait donné naissance à l’économie pure, et même, en dernier lieu, de toute considération d’utilité ; élargi leur rôle en y recourant non seulement pour représenter la solidarité des transactions, mais aussi la mutuelle dépendance des biens économiques (marchandises ou services producteurs) ; et considérablement agrandi leur champ d’application en l’étendant de l’étude du régime particulier de la libre concurrence à celle des diverses circonstances qui peuvent régir le phénomène économique.

CHAPITRE PREMIER

Les précurseurs de l’emploi des mathématiques en économie politique.

§ I. — Première Période : 1711 — 1800.

La première tentative d’application des mathématiques à la résolution des problèmes économiques paraît dater de 1711, et être due au mathématicien Giovanni Ceva — dont le nom est resté attaché à certains théorèmes importants de la théorie des transversales — qui fit paraître à cette époque, à Mantoue, un petit traité, écrit en latin, ayant pour titre De re nummaria quoad fieri potuit geometrice tractata. Cet ouvrage, comme d’ailleurs la plupart de ceux dont nous aurons l’occasion de parler dans ce premier chapitre, n’a apporté qu’une bien faible contribution à la science ; c’est une œuvre de logique ordinaire à laquelle l’arithmétique est simplement venue prêter son langage. Mais il mérite néanmoins d’attirer l’attention, car on y constate que si G. Ceva n’a pas sa profiter du concours que les mathématiques lui offraient, il n’en a pas moins eu conscience, dès 1711, du grand parti que l’on en pouvait tirer dans l’étude des questions monétaires du fait de la mutuelle dépendance des phénomènes économiques, mutuelle dépendance qu’il a du reste limitée à l’influence de la population et de la quantité de la monnaie sur ce qu’il appelle la valeur externe de celle-ci, par opposition à sa valeur interne, c’est-à-dire à la valeur intrinsèque du métal qui la constitue^[1].

Cette première tentative demeura, semble-t-il, longtemps isolée, et ce n’est que à partir de 1765 qu’apparurent les autres productions mathématico-économiques du xviii^e siècle, d’ailleurs peu nombreuses, dont les principales sont celles de Cesare Beccaria, Henry Lloyd, A.-X. Isnard et Guglielmo Silio^[2].

Cesare Beccaria, le célèbre auteur du Traité des délits et des peines, dans un article intitulé Tentativo analitico sui contrabbandi et publié dans le journal Il caffè^[3], s’est préoccupé, à propos de l’établissement de droits de douane et de la contrebande consécutive, de déterminer analytiquement, avec des symboles algébriques, les risques courus tant par le fisc que par les contrebandiers, montrant par cet exemple que les mathématiques sont applicables à l’étude de toutes les questions, de quelque nature qu’elles soient, dont les données sont susceptibles d’accroissement ou de diminution.

Le major-général Henry Lloyd serait, d’après L. Cossa, l’auteur anonyme d’un Essay on the theory of money, publié à Londres en 1771, essai au sujet duquel W. St. Jevons s’exprime en ces termes : « Bien qu’il soit à peine ébauché et absurde en certaines de ses parties, il ne manque ni d’intérêt ni de science et contient une tentative nette et partiellement satisfaisante d’établissement d’une théorie mathématique de la circulation »^[4].

Mais l’œuvre du xviii^e siècle, de beaucoup la plus importante au point de vue qui nous occupe est le Traité des richesses publié^[5] sans nom d’auteur en 1781, et dû en réalité à l’Ingénieur des Ponts et Chaussées français, Achille-Nicolas Isnard^[6].

Dans le premier livre du premier volume de cet ouvrage — qui en comporte deux — sous le titre Des richesses en général et de leurs rapports, A.-N. Isnard a présenté en effet une véritable « théorie de la valeur » en avance de près d’un siècle sur les idées de son temps. Comprenant que « en parlant de richesses, on ne prend guère le mot valeur dans un sens absolu » et que ce mot exprime le rapport de deux choses que l’on compare pour les échanger », il s’est préoccupé de répondre à ces questions : « Comment les choses acquièrent-elles une valeur dans les échanges ? Comment cette valeur dépend-elle de la quantité des choses et du besoin qu’on en a ? Comment les quantité dépendent-elles du besoin et des valeurs ? Comment les besoins sont-ils subordonnés eux-mêmes aux quantités et aux valeurs ? » Et, seul peut-être avant L. Walras, il a été ainsi amené à concevoir une théorie de l’échange tenant compte, d’une manière restreinte il est vrai, de la mutuelle dépendance des phénomènes économiques, théorie qu’il expose de la manière suivante dans les cas d’un marché isolé soumis au régime de la libre concurrence absolue, et ne comportant que deux ou trois marchandises :

« Il est facile de voir ce qui arriverait dans un échange entre les propriétaires isolés de deux marchandises, dont les besoins du superflu de l’un équivaudraient aux besoins du superflu de l’autre. Si l’on suppose, par exemple, que le superflu des premiers est une quantité a de mesures M d’une marchandise, et que celui des seconds est une quantité b de mesures M’ d’une autre ; ces choses ne pouvant être échangées que l’une contre l’autre, puisqu’on les suppose seules, la quantité a de mesures M équivaudra à la quantité b de mesures M’: ainsi on aura aM = bM’ et par conséquent M : M’:: 1/a : 1/b. La valeur de chaque mesure sera donc en raison inverse de la quantité qui en est exposée en échange. »

« Si au lieu de deux marchandises, on en suppose dans le commerce trois ou un plus grand nombre, il en sera de même pour la valeur générale des marchandises. Chaque mesure particulière sera égale à la somme des offres faites par les propriétaires des autres marchandises divisée par la quantité des mesures, ou, ce qui est la même chose, les valeurs des marchandises seront en raison directe de la somme des offres et en raison inverse de la quantité des mesures. Mais les offres étant composées de plusieurs marchandises hétérogènes, il n’est pas possible de déduire de l’égalité, ou de l’équation dont nous venons de parler, le rapport de deux marchandises particulières ; pour trouver le rapport des marchandises prises deux à deux, il faudrait former autant d’équations qu’il y a de marchandises ; le premier membre de ces équations contiendrait la quantité de marchandises, le second la somme des offres. »

« Soient trois marchandises exposées pour être échangées les unes contre les autres ; soit une quantité a de mesures M de l’une, une quantité b de mesures M’ de l’autre, et une quantité c de mesures M" de la troisième. Soit divisée la quantité a de marchandises M en deux parties am et an, dont chacune soit la somme des parties offertes par chaque propriétaire des mesures M pour recevoir des mesures M’et M" ; soit divisée la quantité b de marchandises M’en deux parties bp et bq, dont chacune soit la somme des parties offertes par chaque propriétaire des mesures M’ pour recevoir des mesures M et M" ; soit divisée la quantité c de marchandises M" en deux parties cr et cs, dont chacune soit la somme des parties offertes par chaque propriétaire des mesures M" en échange des mesures M et M’. Ces suppositions donnent trois équations aM = pbM' + rcM . bM' = maM + scM", cM = qbM' + naM. On peut déduire de ces trois équations les rapports des marchandises prises deux à deux, et l’on aura

M : M’: M" ${\frac {r+p-pr}{a}}:{\frac {s+m-sm}{b}}:{\frac {n+q-nq}{c}}$

on peut en déduire aussi la valeur de chaque marchandise relativement à chaque autre, et les quantités que chaque propriétaire attirera en échange de ses offres »^[7].

Cette théorie de l’échange — que nous avons crû devoir reproduire parce qu’elle constitue sans doute la plus ancienne ébauche de celles que nous rencontrerons par la suite — est complétée par une théorie de la monnaie, dans laquelle A. N. Isnard s’attache à montrer que la monnaie est une marchandise comme les autres, dénuée de vertus particulières. Quant au reste de l’ouvrage, nous nous abstiendrons d’en parler, non qu’il soit dénué d’intérêt, il contient au contraire de bonnes critiques des idées de Quesnay et des «  Économistes », mais parce que les mathématiques n’y jouent aucun rôle.

Pour en finir avec les auteurs du xviii^e siècle, il ne nous reste plus qu’à dire quelques mots de l’œuvre du palermitain Guglielmo Silio qui, de même que G. Beccaria, et sans doute à son imitation, a fait porter ses recherches sur les questions de contrebande. Son Saggio su l’influenza dell’ analisi nelle scienze politiche ed economiche applicata ai contrabbandi^[8] a pour objet la résolution de cinq problèmes du premier desquels voici^[9], à titre d’exemple, l’énoncé : « Connaissant le droit dédouane, le prix de la marchandise susceptible de donner lieu à la contrebande, le nombre des circonstances favorables au marchand et celui des circonstances favorables au fisc (Regalia), déterminer la peine qu’il convient d’appliquer au marchand et la somme à percevoir par le fisc », et il se termine par cette conclusion typique : « Qui donc serait assez audacieux ou insensé pour pouvoir espérer obtenir, sans l’aide du calcul, des résultats si nombreux et si importants pour l’exacte balance de l’État ».

§ 2. — Deuxième Période : 1800-1870^[10].

Peu nombreuses au xviii^e siècle, les productions mathématico-économiques sont au contraire devenues très abondantes dès le début du xix^e ; aussi, dans ce rapide historique laisserons-nous de côté les auteurs qui sont restés ignorés à juste titre, tels que Du Mesnil-Marigny ou Esmenard du Mazet, pour ne nous arrêter qu’à ceux qui se sont fait remarquera un titre quelconque, ou dont les œuvres semblent avoir exercé une influence sur le développement de l’économie mathématique. Ces derniers sont, croyons-nous, en France : N.-F. Canard, A. Cournot et E.-J. Dupuit ; en Allemagne : H. von Thünen et H. von Mangoldt ; en Angleterre : W. Whewell et Fleeming Jenkin ; enfin, en Italie : L.-M. Valeriani et F. Fuoco.

Les Principes d’économie politique de François-Nicolas Canard, publiés à Paris en 1801, constituent certainement l’une des plus mauvaises tentatives d’application des mathématiques à l’économie politique. Assez confus et verbeux dans leur ensemble, ils n’offrent dans leur partie mathématique, qui porte principalement sur « la détermination du prix des choses », qu’une simple traduction en symboles d’idées préconçues, traduction qui vient d’ailleurs ajouter aux erreurs économiques dont ces idées sont parfois l’expression des erreurs purement analytiques, car, quoique professeur de mathématiques, F.-N. Canard « ignore ou oublie les éléments du calcul des fonctions »^[11]. En un mot, ainsi que le dit A. Cournot, « ces prétendus principes sont si radicalement faux, et l’application en est tellement erronée, que le suffrage d’un corps éminent n’a pu préserver l’ouvrage de l’oubli »^[12]. Le livre de F.-N. Canard présente en effet cette particularité d’être le seul ouvrage d’économie politique mathématique qui ait reçu en France une sorte de consécration officielle, et c’est à ce titre que nous n’avons pas voulu le passer sous silence. Écrit pour donner sous la forme d’ « un chaînon d’une suite de conséquences » une réponse négative à cette question mise au concours par l’Institut : Est-il vrai que dans un pays agricole, toute espèce de contribution retombe sur les propriétaires fonciers ?, il fut couronné par cette assemblée. Il est vrai que ce fut « faute de mieux », nous dit Blanqui^[13], ce qui est évidemment une explication, mais qui n’est peut-être pas suffisante pour répondre à ces interrogations de Joseph Bertrand : « Comment [Canard] devint-il lauréat de l’Institut ? Sur le rapport de quelle commission ? Je n’ai pas eu l’indiscrétion de le chercher »^[14].

Luigi Molinari Valeriani, d’Imola, et Francesco Fuoco, de Naples, sont les deux derniers membres de ce groupe d’auteurs, dont nous avons déjà cité plusieurs noms, qui, à la naissance même de l’économie mathématique, à la fin du xviii^e siècle et au début du xix^e siècle ont largement représenté l’Italie, qui compte, aujourd’hui encore, les plus nombreux adeptes de cette science^[15].

L.-M. Valeriani est un des premiers qui — à la suite de P. Verri et de Frisi — aient essayé d’élaborer une théorie scientifique de la détermination des prix par le seul jeu de l’offre et de la demande. Il a été ainsi conduit à introduire dans son analyse, à côté de la notion de la valeur d’usage (pregio), la notion de la valeur spécifique (pregio specifico), sorte de valeur d’échange intrinsèque proportionnelle à la demande i et inversement proportionnelle à l’offre o de la marchandise considérée, c’est-à-dire représentée par la formule $p={\frac {i}{o}}$ qu’il s’est attaché à établir et à justifier<^[16] dans deux discours, publiés à Bologne en 1810 et 1817, respectivement intitulés Apologia della formola $p={\frac {i}{o}}$, trallandosi del come si determini il prezzo delle cose tulle mercatabili, contro ciò che ne dice il celebre autore del « Nuovo prospetto delle scienze economiche »^[17] et Discorso apologetico in cui si sostiene recarsi invano pel celebre autore del « Nuovo prospetto delle scienze economiche » contro l’apologia della formola $p={\frac {i}{o}}$ trallandosi del come si determini il prezzo delle cose tulle mercatabili, ciò che il medesimo ha scritto nel tomo II, in pag. 114-117, 141-146 ed net IV, pag. 214-219, 244-263 del opera susdetta^[18].

Quant à F. Fuoco, qui, dans ses Saggi economici, — publiés à Pise en 1825-27, mais dont la valeur n’a été reconnue que plus tard par Antonio Scialoja — a été le premier des auteurs italiens à montrer l’importance des théories de Ricardo, il présente, d’après L. Cossa^[19], l’originalité d’avoir répondu par avance dans cet ouvrage à l’objection de ceux qui invoquent contre l’emploi des mathématiques en économie politique, l’impossibilité d’assujettir les prémisses à une détermination mathématiquement exacte, tout en fixant lui-même des limites trop étroites à cet emploi.

L’ordre chronologique que nous suivons dans cette rapide revue nous amène à parler maintenant de Heinrich von Thünen, son Isolirte Staat in Beziehung auf Landwirthschaft und Nationalökonomie, oder Untersuchungen über den Einfluss, den die Getreidepreise, der Reichtum des Bodens und die Abgaben auf den Ackerbau ausüben ayant été publié à Hambourg en 1826^[20]. Il convient toutefois de noter que ce n’est guère dans cette partie de l’œuvre de H. von Thünen, désignée sous le nom générique de l’État isolé, mais bien plutôt dans la seconde partie éditée en deux volumes^[21] parus à Rostok en 1850 et 1863, sous le titre Der isolirte Staat…, Der naturgemässe Arbeitstohn und dessen Verhältniss zum Zinsfluss und zur Landrente, que l’on rencontre des applications des mathématiques à la solution de problèmes d’économie politique. Dans la première partie en effet, le savant agronome mecklembourgeois a étudié uniquement des questions d’économie rurale, tandis que dans la seconde il a voulu profiter de l’expérience qu’il avait acquise dans l’exploitation de son domaine de Tellow pour essayer d’élucider les diverses questions de salaire, d’intérêt et de rente qui étaient déjà à cette époque à l’ordre du jour des économistes. Or, c’est principalement dans ce dernier travail qu’il a jugé à propos de recourir à l’algèbre pour donner aux résultats de ses observations des formes synthétiques permettant d’en tirer des conclusions précises, telles que la fameuse loi d’après laquelle le salaire naturel serait la moyenne proportionnelle entre la valeur de ce qui est indispensable à l’ouvrier et celle de ce qu’il produit à l’aide du capital dans une exploitation considérable, le reste du produit formant le revenu du capitaliste et donnant le taux naturel de l’intérêt du capital. Mais ce n’est d’ailleurs que rarement que H. von Thünen a entendu chercher dans les mathématiques un moyen d’investigation, et le plus souvent, comme ses prédécesseurs, il s’est borné à leur demander un langage commode pour enregistrer des conclusions auxquelles il était parvenu sans en faire usage. Aussi croyons-nous que s’il jouit d’un certain prestige parmi les économistes mathématiciens, il ne le doit pas tant aux formules algébriques figurant dans son œuvre qu’à cette impression générale qui s’en dégage, que c’est là l’œuvre d’un esprit scientifique pénétré des notions de continuité et de limite qui échappent souvent aux ἀγεωμετρητοί et qui ont tout naturellement permis à H. von Thünen de devancer les théories de l’utilité ou de la productivité marginales, par exemple lorsqu’il dit que c’est « l’utilité de la dernière parcelle de capital employée qui détermine le taux du revenu de la totalité de la somme prêtée »^[22].

Sur William Whewell qu’il nous reste à signaler avant d’arriver à A. Cournot, nous serons bref. Nous en dirons simplement que si l’on désirait disposer méthodiquement, dans une bibliothèque par exemple, les œuvres des auteurs que nous sommes en train de passer rapidement en revue, il serait tout indiqué de placer ses œuvres à côté de celles de F.-N. Canard, à moins qu’on ne préfère les mettre en pendants du fait de la différence des sujets choisis. Ses divers mémoires ayant pour objet tant la Mathematical exposition of some [et certain] doctrines of political economy que la Mathematical exposition of the leading doctrines in Ricardo’s « Principles of political economy and taxation » dont la publication dans les Cambridge philosophical transactions^[23] valu à W. Whewell une certaine célébrité, n’offrent en effet, comme l’ouvrage du lauréat de l’Institut, que des traductions en symboles algébriques sous le prétexte qu’elles traitent de quantités, de théories économiques préexistantes. Ces traductions se différencient cependant de celles de N.-F. Canard en ce que W. Whewell a repris les idées de spécialistes autorisés au lieu d’adopter tout simplement, comme son prédécesseur, celles qui avaient ordinairement cours autour de lui ; mais cette différence ne parait pas suffisante pour empêcher de telles productions d’être, les unes comme les autres, de véritables non-sens — selon la forte expression de W. St. Jevons^[24].

Antoine-Augustin Cournot est le premier économiste qui ait essayé de faire une œuvre mathématico-économique réellement constructive, et d’arriver « de manière évidente à la connaissance des faits en partant de l’ignorance de ces mêmes faits »^[25], c’est-à-dire qui ait réellement employé les mathématiques comme moyen d’investigation au lieu de se borner à les utiliser pour traduire ou pour commenter des théories plus ou moins préconçues. Aussi, la plupart des auteurs ont-ils l’habitude de présenter cet éminent mathématicien comme le fondateur de l’économie pure, bien que, en réalité, il n’ait fait état dans son œuvre ni du principe de l’utilité finale, qui fut l’occasion de la naissance de cette science, ni du fait de la mutuelle dépendance économique (dont il avait pourtant nettement conscience qui en est la raison d’être. Cependant, si A. Cournot ne peut guère être considéré comme le fondateur de l’économie pure, il est incontestablement le plus considérable de ses précurseurs, et ses Recherches sur les principes mathématiques de la théorie des richesses, publiées à Paris en 1838, sont très importantes et très remarquables surtout pour l’époque à laquelle elles ont été écrites.

Dans cet ouvrage, duquel il a éliminé « les questions où l’analyse mathématique n’a aucune prise »^[26], A. Cournot — comme la plupart des économistes mathématiciens qui n’ont pas su abandonner toutes visées pratiques pour se livrer à des études exclusivement scientifiques dans le seul but de savoir — s’est proposé d’élaborer une théorie de la valeur ou de la détermination des prix. Après toute une série de considérations plus ou moins philosophiques sur la valeur, et un exposé de la question du change qui ne semble pas présenter de grands caractères d’originalité, il a abordé cette théorie par l’examen du problème dont la solution est le plus directement accessible aux mathématiques, celui du monopole. Supposant connue expérimentalement la « loi du débit » ou « de la demande » d’une marchandise en fonction décroissante de son prix de vente uniquement, il a cherché la grandeur de ce prix la plus avantageuse pour un monopoleur, d’abord dans le cas où les frais de production sont négligeables (eau minérale naturelle), et ensuite dans celui où ces frais sont appréciables (eau minérale artificielle ou produit pharmaceutique de composition secrète ; en se préoccupant en outre de l’influence de l’impôt sur le coût de ces marchandises. Puis, du cas où un seul individu jouit du monopole, il est passé à celui où deux individus se partagent ce monopole, pour en arriver finalement à la libre concurrence considérée comme le cas limite où le nombre des monopoleurs devient infini, si toutefois il est permis de s’exprimer ainsi. Mais, tandis qu’il avait fait une ce analyse magistrale » (F.-Y. Edgeworth) du premier cas, A. Cournot a commis dans la généralisation de sa théorie de graves erreurs qui ont donné naissance, dans des conditions que nous rappellerons plus loin, à toute une série de discussions auxquelles M.-V. Pareto^[27] paraît avoir mis fin en montrant que si la solution du problème de la détermination du prix d’une marchandise dont la production serait entre les mains de deux monopoleurs est indéterminée (comme l’a indiqué M. F.-Y. Edgeworth^[28]), ce problème ne peut en réalité se poser par suite de l’incompatibilité des équations traduisant pour chacun des producteurs le fait que ce producteur est un monopoleur. Enfin, après avoir étudié la détermination du prix de chaque marchandise, A. Cournot a essayé de réaliser la synthèse du système économique à partir des éléments qu’il en avait dissociés — ce qui constituait évidemment une utopie^[29], car il était clair qu’il ne pouvait retrouver les éléments qu’il avait précédemment négligés — en faisant parfois, pour l’harmonie de ses démonstrations, trop bon marché des circonstances accessoires. De minimis non curat prætor ! Ajoutons que l’interprétation géométrique de l’équation à laquelle il est parvenu analytiquement a conduit A. Cournot à faire figurer, pour la première fois croyons-nous, dans la détermination des prix de véritables courbes de demande et d’offre représentant les variations de la demande ou de l’offre d’une marchandise en fonction de son prix^[30].

Malgré l’intérêt qu’elles présentent, malgré la réputation de leur auteur comme mathématicien, les Recherches, venues avant leur heure, passèrent complètement inaperçues : elles ne furent mentionnées ni dans la bibliographie de l’Histoire de l’économie politique de Blanqui ni dans le Répertoire général d’économie politique de Coquelin, ni même dans le Dictionnaire de l’économie politique publié par Guillaumin. Aussi, A. Cournot, découragé par cet insuccès, ainsi qu’il le dit lui-même, reprit-il en 1863 l’exposé de ses conceptions économiques, en les dégageant de toutes équations, dans un livre intitulé Principes de la théorie des richesses, qui fut du reste dans la suite jugé bien inférieur à sa première œuvre, dont on finit en effet par reconnaître la réelle valeur lorsque L. Walras et W. St. Jevons eurent attiré l’attention sur elle : le premier, en exprimant publiquement le regret que justice n’ait pas été rendue à celui qu’il considérait comme son maître, dans un mémoire qu’il présenta en 1873 à l’Académie des sciences morales et politiques, et dont J. Bertrand prit prétexte pour émettre sur l’ouvrage de A. Cournot des critiques qui, portant à faux, donnèrent lieu aux discussions dont nous avons eu précédemment l’occasion de parler ; le second, en rendant, dans la préface de la seconde édition de sa Theory un éclatant hommage à l’œuvre économique du mathématicien français. Il est d’ailleurs intéressant de signaler que c’est surtout à l’étranger^[31], en Angleterre et aux États-Unis notamment, que s’est établie la réputation de A. Cournot en tant qu’économiste. C’est ainsi qu’un long article lui est consacré dans le {{lang|en|Dictionary of political economy}} de R.-H. Inglis Palgrave, et que ses Recherches ont eu le rare honneur d’être traduites en Anglais^[32], alors que son nom était presque oublié en France et que son livre était devenu introuvable en librairie.

L’ingénieur des Ponts et Chaussées, Étienne-Juvénal Dupuit, est bien connu comme économiste. Néanmoins ses œuvres ne tiennent pas une place très considérable parmi celles dont nous nous occupons ici, car, bien que cet auteur eût une grande habitude des mathématiques (ses ouvrages techniques le prouvent), il ne s’est guère soucié en général de faire appel à cette science dans ses recherches économiques. On lui doit cependant deux articles : l’un sur la mesure de l’utilité des travaux publics, l’autre sur l’influence des péages sur l’utilité des voies de communication, publiés l’un et l’autre dans les Annales des Ponts et Chaussées en 1844 et en 1849, qui présentent un grand intérêt au point de vue de la genèse de l’économie politique pure. Dans ces articles — qui ont pour objet des questions de monopole à propos desquelles il a renouvelé, à son insu sans doute, les théories de A. Cournot — E.-J. Dupuit a en effet fait ressortir, pour la première fois semble-t-il, le fait de la « gradation de l’utilité » (W. St. Jevons), dont une analyse plus approfondie a donné naissance à l’économie mathématique. Il a montré que l’utilité d’un objet n’est pas mesurée par le sacrifice que l’on fait effectivement pour se procurer cet objet, ainsi que le prétendait J.-B. Say, mais par le sacrifice que l’on serait disposé à faire, et que, par suite, « l’utilité d’un morceau de pain peut croître pour le même individu depuis zéro jusqu’au chiffre de sa fortune entière ». Mais après avoir ainsi défini l’utilité d’un objet par ce que W. St. Jevons a appelé plus tard la désutilité (disutility) du sacrifice que l’on serait disposé à faire pour se le procurer, E.-J. Dupuit a cru pouvoir évaluer cette utilité par l’expression pécuniaire de ce sacrifice, telle qu’elle est fournie par la loi de variation de la demande en fonction du prix, que A. Cournot a appelée loi du débit, et qu’il a désignée sous le nom de loi de consommation. Or, il est évident que non seulement l’utilité de la monnaie diffère d’un individu à un autre, mais encore qu’elle varie pour un même individu suivant les circonstances ; en la prenant comme base d’évaluation, E.-J. Dupuit a donc commis une grave faute de raisonnement^[33], dont on ne saurait cependant lui tenir rigueur, car depuis lors bien d’autres, qui n’avaient pas l’excuse d’être des innovateurs, sont tombés dans la même erreur.

Hans von Mangoldt, quoique n’appartenant pas à la même classe que les derniers auteurs que nous venons de rencontrer, s’est néanmoins placé à l’avant-garde des économistes mathématiciens. Dès 1863 — l’année même où A. Cournot a renoncé à l’emploi des mathématiques — il s’est en effet avisé, dans son Grundriss der Volkswirthschaftslehre publié à Stuttgart, de recourir à des représentations graphiques pour expliquer la détermination des prix courants des marchandises, en montrant, ainsi qu’on l’a fait bien souvent depuis, que ces prix courants correspondent aux points d’intersection de courbes de demande et de courbes d’offre représentant en fonction des prix les quantités de marchandises offertes ou demandées^[34]. Il s’est en outre préoccupé dans le même ouvrage de la question si importante, au point de vue de l’économie pure, des marchandises concurrentes et des marchandises complémentaires. Mais sa tentative n’eut sans doute pas plus de succès que celle de A. Cournot, car son livre a subi un sort analogue à celui de son prédécesseur, en ce sens que, de même que A. Cournot crut devoir éviter les mathématiques dans ses Principes (qu’il fit paraître à la suite de l’insuccès de ses Recherches), de même l’éditeur de la seconde édition du Grundriss^[35] jugea opportun de supprimer les courbes qui figuraient dans la première. Il y a d’ailleurs lieu de noter que, du fait de cette suppression, cette partie de l’œuvre de H. v. Mangoldt reste souvent ignorée, et c’est pour cette raison que nous avons pensé intéressant de la rappeler ici, d’autant plus que ce savant professeur de Gœttingen est bien connu par ailleurs pour ses travaux sur la théorie de la rente et « extensions », qui sont venus compléter dans une certaine mesure ceux de F.-B.-W. Hermann, dont nous aurions peut-être pu faire figurer également le nom parmi ceux des économistes mathématiciens, car, remarquons-le en passant, ce sont souvent des économistes mathématiciens — H. v. Thünen, H. v. Mangoldt, A. Marshall, L. Walras, V. Pareto, etc., — qui sont venus perfectionner cette théorie.

Nous terminerons notre liste des précurseurs avec le nom de Fleeming Jenkin, qui vient du reste la clôturer dignement. À la vérité, on ne doit guère de conceptions économiques nouvelles à cet éminent professeur d’« engineering » de l’université d’Edimbourg, car, sans s’en douter, il n’a, le plus souvent, que redécouvert les théories de A. Cournot ou de E.-J. Dupuit. C’est ainsi qu’il a repris en considération les variations de la demande et aussi celles de l’offre en fonction des prix et montré que « sur un marché donné, à un instant donné, le prix courant d’un produit est celui auquel les courbes d’offre et de demande se coupent » — dans un article sur les Trade Unions publié dans le numéro de mars 1868 de la North British Review, et dans un travail sur The graphic representation of the laws of supply and demand, and their application to labour figurant dans les Recess Studies éditées à Edimbourg en 1870 par A. Grant — et qu’il s’est trouvé inspiré des mêmes idées que E.-J. Dupuit^[36] dans un mémoire on the principles which regulate the incidence of taxes présenté à la session 1871-72 de la Royal Society of Edimbourg. Mais s’il a suivi un chemin déjà frayé, F. Jenkin a certainement, par la netteté et la précision qu’il a apportées dans ses ouvrages, fourni une large contribution aux travaux d’élagage qui ont permis à tant d’autres de s’engager par la suite dans la même voie^[37].

CHAPITRE II

Les fondateurs de l’économie pure.

§ 1. — Hermann Heinrich Gossen.

Bien que nous le signalions le premier parmi les fondateurs de l’économie pure, H. Gossen^[38] n’est pas au nombre de ceux qui ont le plus illustré l’emploi des mathématiques en économie politique ; il s’est en effet contenté, en général, de la grossière approximation consistant à attribuer, aux fins de simplicité, des lois linéaires aux variations de l’intensité du plaisir ou de la peine en fonction, soit de la durée de la jouissance ou du travail qui les procure, soit des quantités de produits dont ils dépendent, ce qui l’a conduit à formuler des résultats d’une précision purement apparente^[39]. Et même, malgré la multiplicité des graphiques, des symboles et des tableaux que l’on rencontre dans son œuvre, on pourrait le rattacher à l’École autrichienne presqu’aussi bien qu’à celle de Lausanne, car tout cet appareil sert à expliquer et à commenter les théories plutôt qu’il n’est indispensable à leur démonstration Mais H. Gossen fut le premier membre de ce petit groupe de penseurs originaux, comprenant avec lui W. St. Jevons, K. Menger et L. Walras, qui, au coups de la seconde moitié du dernier siècle, ont énoncé, sous une forme ou sous un autre, le principe de l’utilité finale^[40], dont la découverte fut le point de départ de l’économie mathématique.

Malgré cette importante contribution à la science, cet économiste demeura longtemps ignoré, et léserait sans doute encore aujourd’hui si W. St. Jevons et L. Walras n’avaient tenu à honneur de ne pas laisser dans l’ombre ce devancier à qui ils n’étaient nullement redevables de leurs théories. Le seul ouvrage que l’on doit à H.-H. Gossen, l’Entwickelung der Gesetze des memchlichen Verkers, und der daraus fliessenden Regeln für menschliches Handeln^[41], n’eut en effet aucun succès lors de sa publication, de telle sorte que les éditeurs, Frederick Vieweg et Fils, ne tardèrent pas à en restituer tous les exemplaires restés entre leurs mains à l’auteur, qui passa ainsi inaperçu au point de n’être même pas mentionné dans l’histoire de l’économie politique en Allemagne^[42] due à Roscher, « un homme qui a tout lu », suivant l’expression du professeur N.-G. Pierson. Ce ne fut que près d’un quart de siècle plus tard que l’importance du livre de H. Gossen fut révélée aux économistes, non pas, comme le veut la légende, grâce à la découverte fortuite, à la bibliothèque du British Museum, du dernier exemplaire qui en aurait subsisté, mais, en réalité, dans les circonstances suivantes :

Le professeur Robert Adamson avait noté, dans la Theorie und Geschichte der National-Oekonomik^[43] de J. Kautz (vol. I, p. 9), une brève référence à un livre contenant, est-il dit, une théorie du plaisir et de la peine écrite par un auteur allemand appelé H. -H. Gossen. Comme il savait que son prédécesseur au collège Owens, W. St. Jevons, poursuivait, des études dans le même ordre d’idées, R. Adamson entreprit aussitôt des recherches pour se procurer le livre en question. Mais ce recherches furent vaines, et ce ne fut que quelques années plus tard, en août 1878, qu’il finit par pouvoir en acquérir un exemplaire, qu’il avait découvert par hasard dans le catalogue d’un libraire allemand, et en faire une analyse qu’il communiqua à W. St. Jevons. Celui-ci s’aperçut aussitôt, non, semble-t-il, sans un certain dépit bien compréhensible, que H. Gossen avait, déjà clairement élucidé les principaux points de la théorie, de l’échange dont il avait lui-même quatre ans plus tôt — ainsi que nous le verrons — revendiqué la priorité sur L. Walras. Il s’empressa alors de signaler cette a antériorité » à ce dernier le 15 septembre 1878, et l’année suivante, il n’hésita pas à présenter H. -H. Gossen au monde économique en lui faisant une large place dans la préface de la seconde édition de sa Theory of political economy. Ce n’est cependant pas à W St. Jevons que H. Gossen doit la plus grande part de sa renommée actuelle, mais à L. Walras, qui, dès qu’il avait eu connaissance de l’Entwickelung, s’en était procuré un exemplaire, non sans peine d’ailleurs, et s’était entouré de renseignements sur son auteur, de telle sorte qu’en 1881 il était à même d’écrire sur l’œuvre et la vie de H.-H. Gossen, et pour la plus grande gloire de cet « Économiste inconnu », une étude très documentée, qu’il fit paraître, après la mort de W. St. Jevons, dans le Journal des Économistes^[44], en vue d’établir nettement les positions respectives des fondateurs de l’économie pure.

⁂

L’ouvrage de H.-H. Gossen constitue, à notre sens, le livre le plus rébarbatif qui puisse tomber sous les yeux d’un lecteur avide d’économie mathématique. Il forme en effet un volume compact de 277 pages, sans division en sections ni chapitres, dont les diverses parties, séparées par de simples tirets, sans titres, offrent, en un style bien allemand, diffus et « emberlificoté », un mélange d’exposés théoriques et de considérations morales à tendances pratiques dont on ne saurait affronter la lecture si l’on n’a pas le cœur blindé de l’aes triplex dont parle Horace.

On peut néanmoins diviser le livre en deux parties : l’une, d’économie pure, comprenant les lois de la jouissance et du travail accompagnées de tableaux arithmétiques, les lois de l’échange et la théorie des rentes ; l’autre, d’économie appliquée, comprenant les règles de conduite relatives aux besoins et aux plaisirs et la réfutation de certaines idées relatives à l’éducation, au crédit et à la propriété.

Au début de son ouvrage, Gossen, qui n’était pas précisément modeste, — le titre prétentieux qu’il a donné à son livre l’indique suffisamment — commence par revendiquer, non sans quelques formes, il est vrai, une place à côté de Copernic, sous le prétexte que ses découvertes sont de nature à faire connaître aux hommes la voie où ils rencontreront le maximum de bonheur de même que les découvertes du célèbre astronome permirent de déterminer les chemins suivis par les corps célestes. Puis, après avoir posé en principe que la méthode mathématique est la seule rationnelle en économie politique, tout en promettant, par égard pour le lecteur, de ne recourir à l’emploi de l’analyse que dans les questions de minima et de maxima, il entre dans le vif de son sujet : l’étude du plaisir et de la peine en vue de la détermination des conditions permettant à chacun de réaliser la plus grande somme de satisfaction possible tout en étant susceptibles, d’après lui, d’assurer, par surcroît, le bonheur de la collectivité.

Gossen part de la loi naturelle de décroissance en fonction du temps du plaisir procuré pour une consommation donnée, et il infère de cette loi, dont il illustre l’exposé au moyen de graphiques, qu’un individu, qui n’a pas le temps d’épuiser plusieurs sources de jouissance, doit user de chacune d’elles dans une proportion telle que les grandeurs des diverses satisfactions réalisées au moment de l’arrêt soient égales entre elles. Il pose ensuite en principe que l’utilité — il dit la valeur d’usage (Werth) — d’un objet est mesurée par la quantité de plaisir que cet objet est susceptible de procurer, ce qui le conduit à classer les objets en trois catégories : 1^o les produits de consommation ; 2^o les produits complémentaires ; 3^o les moyens de production. Puis, l’utilité ainsi déterminée, sans plus s’inquiéter de l’interdépendance des biens économiques dont il avait pourtant conscience, — cela résulte de la classification précédente — il est directement amené à reconnaître à cette utilité une loi de décroissance parallèle à celle des variations du plaisir, d’où il déduit, pour achever la théorie de la jouissance, cette règle pratique, qui est restée à la base de l’économie mathématique : « Lorsque ses ressources sont insuffisantes pour lui permettre de se procurer de tous les biens possibles à satiété, l’homme doit se procurer de chacun d’eux dans une proportion telle que la valeur d’usage du dernier atome soit la même pour tous les biens » (Wenn seine Kräfte nicht ausreichen alle möglichen Genussmittel sich vollauf zu verschaffen, muss der Mensch sich ein jedes so weit verschaffen, dass die letzten Atome bei einem jeden noch für ihn gleichen Werth behatten.)

La théorie du travail fait suite, ainsi que nous l’avons dit, à celle de la jouissance. Gossen la fait reposer tout entière sur ce principe, que l’utilité d’un produit quelconque ne doit être appréciée que déduction faite de la peine correspondant au travail de production, peine qui est d’ailleurs une fonction croissante de la durée de ce travail. Aussi la conclusion en est-elle que l’homme doit répartir ses efforts de telle manière que son travail ne se prolonge jamais au delà du point où l’utilité du produit est égale à la peine de production.

Quant à la théorie de l’échange, confondue avec celle de la production, qui termine la partie scientifique de l’Entwickelung, elle est en quelque sorte la conséquence de celle de la jouissance. Le troc a, en effet, pour raison d’être un accroissement d’utilité au profit des échangistes ; et c’est précisément ce que fait ressortir Gossen, qui en infère qu’il n’y a lieu de continuer à pratiquer l’échange que jusqu’au moment où l’utilité des portions à donner ou à recevoir deviennent égales, cependant qu’il assigne à la réalisation du maximum d’utilité les conditions suivantes dont Walras a pu critiquer, ajuste titre, le défaut d’adaptation à un régime individualiste^[45] : « Pour qu’un maximum de valeur d’usage soit réalisé par l’échange, il faut qu’après lui chaque produit soit réparti entre tous les hommes, de telle sorte que le dernier atome échu à chacun d’eux soit de nature à lui procurer la même jouissance que le dernier atome du même produit à chacun des autres »^[46].

Nous ne nous arrêterons pas à la théorie de la rente, d’ailleurs traitée d’une manière très générale, qui figure à la fin de la première partie du livre de Gossen, non plus qu’aux spéculations sociales qui en constituent la seconde partie, parce que l’examen des questions d’économie appliquée sort du cadre de notre travail. Du reste, cette seconde partie n’est que la conséquence de la première ; son unique objet est l’exposition des conditions pratiques — la nationalisation du sol, par exemple, dont Gossen, à la différence des autres «  nationalisateurs  », n’entend pas fonder le principe sur l’illégitimité de la propriété foncière^[47] — considérées par l’auteur comme susceptibles de mettre chacun à même de réaliser le maximum de satisfaction possible indiqué par la théorie.

Ainsi toute l’œuvre de Gossen n’est qu’un vaste commentaire du principe fondamental de l’économie pure. Aussi, semble-t-il que, dans leur désir de lui rendre largement justice, Jevons et surtout Walras^[48], heureux sans doute de retrouver dans son livre les théories qui leur étaient chères, aient été un peu prodigues d’éloges à son égard, et qu’au contraire M, Edgeworth se soit beaucoup rapproché de la vérité lorsque — sans cependant aller aussi loin que M. Pantaleoni qui, en la faisant remonter à D. Bernouilli, Laplace et Quetelet, ne laisse même pas à Gossen l’honneur de la découverte du principe de l’utilité finale — il formula son opinion en ces termes : « Gossen paraît avoir été un simple spécialiste aux idées de peu de valeur à l’exception d’une seule, qui l’a rendu immortel »^[49].

§ 2. — William Stanley Jevons.

L’œuvre de W. St. Jevons est trop connue dans son ensemble pour qu’il y ait lieu de nous attarder à des généralités sur cet auteur, qui fut le premier économiste de son époque en Angleterre. Aussi entrerons-nous immédiatement dans le vif de notre sujet en abordant de plano l’examen de ses conceptions sur l’économie mathématique, telles qu’elles sont exposées dans sa Theory of political economy^[50].

Comme Bastiat et bon nombre d’économistes anglais, Jevons est parti de ce principe que la théorie de la valeur est l’essence même de la science pure, mais, sans s’arrêter à l’affirmation de Mill que tout était dit sur cette théorie, il a entrepris de l’édifier sur une base qu’il considérait comme nouvelle. Au lieu de rechercher l’origine, voire la cause, de la valeur dans le travail de production, comme la plupart de ses prédécesseurs — notamment Mill et Ricardo, auxquels il a fait, à tort ou à raison^[51], le reproche de ne s’être pas rendu compte que le coût de production n’est pas l’élément fondamental de la détermination des prix, — il s’est attaché, sous l’influence de Bentham, Senior, Jennings, etc., à montrer que cette valeur ne dépend que de l’utilité des produits. Par suite, sa Theory of poilitical economy n’est pas, à proprement parler, autre chose qu’un exposé, sous une forme plus ou moins mathématique ; des principes de la science économique à partir de la seule notion d’utilité. D’après ce que nous avons vu précédemment, ce n’était évidemment pas là un point de départ aussi nouveau que Jevons se l’était tout d’abord imaginé ; puisque, ainsi qu’il a été le premier à le reconnaître ultérieurement^[52], Gossen l’avait tout à fait devancé quant aux principes et à la méthode de l’Économique, mais l’économiste anglais n’en a pas moins eu le mérite de l’originalité. En effet, lorsque, en 1862, il présenta une première esquisse de sa théorie au congrès de Cambridge de la British Association^[53], non seulement il ne connaissait pas l’œuvre de Gossen, mais encore il ne pouvait lui être fait grief de son ignorance, car l’exemplaire de l’ouvrage de Gossen, dont nous avons eu l’occasion de signaler l’existence à la bibliothèque du Britisih Museum, n’a été acquis par cet établissement qu’en 1865. D’ailleurs, lors même qu’il eût sciemment repris les idées de Gossen, ce qui n’est pas le cas, Jevons n’en mériterait pas moins une grande partie de l’honneur de la découverte qu’on a coutume de lui attribuer, car il a apporté dans son exposé des qualités qui faisaient totalement défaut à Gossen : la clarté et la précision qu’il avait sans doute conservées de ses débuts comme chimiste à la monnaie de Sydney et qui caractérisent toutes ses œuvres. Et c’est précisément là ce qui explique, qu’au lieu de rester inconnu comme l’économiste allemand, il ait au contraire fait école, d’où il résulte clairement que son génie était plus réellement créateur que celui de son prédécesseur.

Dans ces conditions, il ne nous semble donc pas superflu d’indiquer les grandes lignes de la Theory of political economy.

Dans l’introduction de cet ouvrage, Jevons pose en principe que « l’Économique, si elle doit être une science, doit être une science mathématique », tout en s’attachant à faire ressortir la compatibilité de l’emploi des mathématiques avec l’économie politique. — Nous avons précédemment (I, I, 1) examiné cette question et indiqué les vues de Jevons à son endroit, nous n’avons donc pas à y revenir. — Puis il présente une théorie quantitative du plaisir et de la peine qu’il considère comme du plaisir négatif, en se préoccupant des divers éléments dont ils peuvent dépendre, tels que : intensité, durée, etc. ; mais ce sont là des considérations qui se rattachent au domaine de la psychologie plutôt qu’à celui de l’économie politique. Enfin, il entre dans son sujet proprement dit par l’étude de l’utilité, montrant ainsi nettement qu’il entendait faire de cette théorie la pierre angulaire de toute son œuvre. Et c’est ainsi» qu’après de nouvelles considérations philosophiques sur les « lois des besoins humains », il arrive à sa « tâche principale » qui est « de montrer la nature exacte et les conditions de l’utilité »^[54].

La théorie de l’utilité de Jevons repose entièrement, comme celle de Gossen, sur le principe de la décroissance de l’utilité d’un produit en fonction de sa quantité, décroissance corrélative à celle du plaisir en fonction de la durée d’une jouissance ; mais elle se distingue largement de celle de l’économiste prussien par la netteté qu’il a apportée dans son exposition. Or, de cette netteté il nous serait difficile de donner une idée même approximative sans faire appel sinon aux symboles du moins au langage mathématique. Aussi croyons-nous préférable de renvoyer intégralement l’exposé de la théorie de l’utilité de Jevons au début de la quatrième partie de ce travail, où cet exposé trouvera naturellement sa place étant donné que cette théorie constitue précisément la meilleure expression des principes dont la découverte a donné naissance à l’économie pure et qui sont restés à la base de cette science.

Quoi qu’il en soit, de sa théorie de l’utilité Jevons déduit directement celles de l’échange et du travail, i. e. de la production, qui constituent la partie la plus importante de son livre et forment à elles seules son système économique.

Dans sa théorie de l’échange il commence par faire ressortir que la valeur (d’échange) d’un produit est essentiellement relative, « qu’elle n’exprime rien d’autre qu’un rapport », d’où il est conduit à poser en principe que « la clé de voûte de toute la théorie de l’échange et des principaux problèmes de l’Économique se trouve dans la proposition suivante : Le rapport d’Échange de deux produits quelconques sera inversement proportionnel aux degrés finals d’utilité des quantités de produits disponibles pour la consommation, après que l’échange est achevé »^[55] ; ce qui revient à dire que l’échange s’établira de telle sorte que l’une des parties nait plus le désir d’acheter ni l’autre de vendre davantage. Et, en effet, il suffit de traduire en symboles cette proposition pour obtenir un système de deux équations permettant de déterminer les deux inconnues du problème de rechange, dans le cas particulier où le marché est limité à deux trafiquants et deux produits (Cf. III, I, 1). Jevons ne borne d’ailleurs pas à ce cas particulier son étude de l’échange. Après avoir ainsi établi la condition de satisfaction maximum et en avoir déduit la formule du partage individualiste, — tandis que Gossen, laissant de côté la condition d’égalité de l’offre et de la demande, avait plutôt envisagé le partage communiste, — il s’est efforcé d’étendre son principe à un marché plus complexe. Abordant le cas où trois échangistes possédant chacun un produit se trouvent en présence sur un marché, il s’est attaché à faire ressortir que quel que soit le nombre des trafiquants, il suffit de décomposer l’ensemble des opérations en échanges simples pour obtenir autant d’équations que le problème renferme d’inconnues, chaque échange donnant naissance à deux équations suffisantes pour déterminer les deux inconnues qu’il implique. Mais ce faisant, il ne semble pas s’être rendu compte qu’à côté de la condition de satisfaction maximum il en est une autre à laquelle il faut se préoccuper de satisfaire dès l’instant où le nombre des échangistes devient supérieur à deux, parce qu’alors elle ne se trouve plus satisfaite ipso facto, c’est la condition de l’unité de rapport d’échange sur le marché, ou, ce qui revient au même, de l’unité de prix. Or, il est clair, ainsi que l’a montré Walras^[56], qu’en l’absence de cette unité de prix, un ensemble de transactions conclues entre trafiquants pris deux à deux ne saurait aboutir à un équilibre général du marché, car certains arbitrages, c’est-à-dire certains échanges entre individus appartenant à des groupes différents, resteraient désirables^[57]. Le procédé de généralisation de ses « équations d’échange », préconisé par Jevons, doit donc, pour le moins, être considéré comme incomplet. Quant à la théorie du travail qui complète le système économique de Jevons, dont la théorie de l’échange forme l’armature, elle est en quelque sorte le pendant ou, plutôt, la contre-partie de celle de l’utilité, dont elle dérive directement. Elle repose, en effet, comme celle de Gossen, sur le fait de la croissance (après une certaine période de décroissance) du degré de pénibilité du travail en fonction de sa durée, et, par suite, de la quantité produite. Jevons a attaché une importance fondamentale à cette théorie parce qu’elle lui a permis — en partant de ce fait que l’individu suspend évidemment son travail au point où le degré d’utilité du dernier élément produit devient égal au degré de désutilité (disutility) de l’effort de production — de montrer que les articles qui s’échangent, d’après ce que nous avons vu, en quantités inversement proportionnelles à leur utilité finale, s’échangent par là même en quantités inversement proportionnelles à leur coût de production. Or, tout en combattant les idées de ceux qui voyaient dans le coût de production la cause de la valeur, il éprouvait le besoin de trouver la confirmation de ses théories dans la concordance des conclusions auxquelles elles conduisaient avec le principe de proportionnalité de la valeur au coût de production, qui avait généralement cours en Angleterre à son époque^[58]. Mais pour ingénieuse que soit cette théorie, elle n’en perd pas moins la plus grande partie de son intérêt dès que l’on abandonne le point de vue particulier auquel s’est placé son auteur, parce qu’elle ne présente qu’une face, la moins importante, de l’équilibre de la production. Dans l’état actuel de la division du travail en effet, l’homme se préoccupe bien moins du rendement de ses efforts que de la valeur d’échange de sa peine, de telle sorte que « le rapport [valeur] d’échange régit la production autant que la production régit le rapport d’échange »^[59], ainsi que Jevons lui-même a été le premier à le reconnaître, encore que, par esprit de réaction contre la théorie du coût de production, il ait été porté à l’exagération en sens contraire, comme en témoigne cette affirmation placée en tête de son ouvrage : « la valeur dépend entièrement de l’utilité »^[60].

L’ouvrage de Jevons est complété par une théorie de la rente reposant sur « cette vérité, que les articles s échangeront en quantités inversement proportionnelles aux coûts de production des portions les plus coûteuses, savoir, les dernières portions échangées »^[61], qui n’offre pas de caractères particuliers ; puis, par une théorie du capital, qu’il s’est efforcé d’exposer « d’une manière plus simple et plus logique que ne l’ont fait quelques-uns des plus récents Économistes »^[62], tout en restant d’accord avec Ricardo ; et enfin, par un certain nombre de considérations sur la population, les salaires, etc., qui n’avaient pu trouver place dans le corps du livre. Nous ne nous arrêterons pas à ces diverses questions dans l’étude desquelles le rôle des mathématiques, déjà peu important dans le reste de l’ouvrage, devient à peu près nul.

La Theory of political economy n’est pas en effet un traité d’économie mathématique, « une vue systématique de l’Économique », mais « une esquisse »^[63] des principes de cette science que, dans un but de propagande, l’auteur, se réservant d’entrer plus tard dans de plus amples développements^[64], s’est attaché à exposer le plus simplement possible. Car, il est important de le noter, pour juger en toute justice de son œuvre, l’économiste anglais était avant tout « désireux de convaincre d’autres économistes que leur science ne peut être étudiée de manière satisfaisante qu’en partant d’une base mathématique explicite »^[65], et c’est uniquement cette base qu’il s’est proposé d’établir. Or, il a si bien réussi, grâce à sa « lucidité brillante et à son style séduisant » (A. Marshall), qu’il est considéré, ainsi que nous le disions au début, comme l’instaurateur de la théorie de l’utilité finale, sur laquelle reposa exclusivement jusqu’à ces derniers temps toute l’économie mathématique. Aussi, sans songer à lui faire grief des lacunes ou des inexactitudes qui ont pu se glisser dans certaines parties de son œuvre qu’il considérait comme accessoires, et dont, à l’occasion, il a reconnu lui-même l’imperfection, Jevons doit-il être considéré comme le fondateur effectif de l’économie pure, encore qu’il ait eu tendance à confondre le domaine de l’Économique avec celui de l’Hédonique^[66], et qu’il se soit parfois montré enclin aux élubrations philosophiques et aux digressions pratiques.

§ 3. — Alfred Marshall.

Il est un autre économiste mathématicien anglais que sa grande situation dans le monde économiste contemporain ne nous permet pas de passer sous silence : c’est le professeur Alfred Marshall de l’Université de Cambridge. On ne saurait guère à la vérité classer M. Marshall parmi les fondateurs de l’économie pure, dont l’étude fait l’objet de ce chapitre, mais comme il est le chef incontesté de l’école anglaise, à laquelle Jevons a imprimé une impulsion nouvelle, nous croyons tout indiqué de lui donner ici une place qu’il nous serait difficile de lui attribuer ailleurs, car, toutes proportions gardées, il y aurait plutôt lieu de le rapprocher de Whewell que des auteurs que nous rencontrerons par la suite, étant donné qu’il n’a fait appel aux mathématiques qu’à titre tout à fait subsidiaire. Il s’est en effet interdit de leur faire jouer le seul rôle qui justifie pleinement leur emploi en économie politique : celui d’auxiliaire puissant permettant d’élucider, après les avoir convenablement débarrassées des circonstances accessoires, les questions trop complexes pour être abordées utilement avec la logique ordinaire ; et cela parce qu’il a entendu envisager immédiatement le phénomène économique dans tous ses détails, au lieu de commencer par en abstraire les éléments essentiels pour les analyser séparément, ainsi que l’on procède en mécanique, par exemple ; de telle sorte qu’il s’est trouvé en présence d’un mécanisme tellement compliqué qu’il n’a pu songer à l’étudier avec le concours des procédés de l’analyse mathématique.

⁂

C’est ainsi que ses Principles of economics^[67] se présentent sous la forme d’un exposé littéraire des doctrines classiques dans lequel les graphiques qui figurent en bas des pages servent simplement à illustrer les idées exprimées dans un texte qui se suffit à lui-même, tandis que les « notes mathématiques » que l’on trouve à la fin de l’ouvrage n’ont pas, en général, d’autre objet que de présenter ces mêmes idées sous une forme plus synthétique ou plus compréhensive. Ces notes sont d’ailleurs de moins en moins étendues au fur et à mesure qu’augmente la complexité des matières discutées, conformément à la conception que M. Marshall s’est faite de l’emploi des mathématiques et qu’il a lui-même précisée en ces termes : « Les applications les plus heureuses des mathématiques à l’économie politique sont celles qui sont courtes et simples, qui emploient peu de symboles et qui visent à projeter un rayon lumineux sur quelque point de détail du vaste monde économique plutôt qu’à le représenter dans son infinie complexité »^[68]. Dès lors, si important que soit cet ouvrage, devenu classique depuis longtemps, il est clair qu’il n’a guère contribué à la constitution du domaine de la science pure, dont l’objet est précisément de représenter sinon l’infinie complexité du monde économique, du moins l’interdépendance des phénomènes qui en fournit les rouages essentiels ; aussi n’en parlerons-nous que brièvement. C’est dans la théorie de la demande et de l’offre que M. Marshall a fait le plus large appel à l’emploi des graphiques. Pour traiter cette question, il a pris une position intermédiaire entre les anciens économistes anglais et Jevons : attribuant la détermination du prix aux actions simultanées du coût de production sur l’offre et de l’utilité finale sur la demande, il a admis que la valeur « se maintient en équilibre entre les deux forces opposées comme la clé de voûte d’une arche »^[69]. Cette conception indique évidemment une tendance à se préoccuper de la mutuelle dépendance économique que le professeur de Cambridge a d’ailleurs concouru, dans une certaine mesure, à mettre en évidence en insistant sur l’existence de produits complémentaires et de produits concurrents (Voir III, IV, 1) notamment dans son analyse de la demande et de l’offre conjointes et composites^[70]. Mais, au demeurant, il ne nous semble pas que l’usage des graphiques auxquels a eu recours M. Marshall ait apporté une bien grande contribution à l’élaboration sur des bases scientifiques de la théorie envisagée. Dès l’instant en effet où l’on ne fait état dans l’étude de la demande et de l’offre que des variations des quantités demandées ou offertes en fonction des prix, sans se préoccuper des autres facteurs de l’équilibre économique — par exemple, des variations de l’utilité finale de la monnaie, que l’auteur des Principles s’est cru autorisé à considérer comme négligeables^[71] — il est, a priori, à peu près évident qu’on ne peut guère aboutir à des résultats sensiblement différents dans l’ensemble de ceux que les économistes littéraires désignent sous le nom de lois de l’offre et de la demande. Et, en fait, ce n’est guère que dans l’explication de phénomènes particuliers, dont l’importance est d’ailleurs loin d’être négligeable, tels que la rente des consommateurs^[72] on la possibilité de la coexistence de plusieurs positions d’équilibre économique, les unes stables et les autres instables^[73], que l’introduction de graphiques a permis au professeur de Cambrige de jeter la lumière sur des questions encore obscures.

Quant aux notes mathématiques, dont nous avons précédemment indiqué l’esprit, elles portent en général sur des points de détails trop isolés pour que nous puissions donner des renseignements globaux à leur égard Seules quelques-unes d’entre elles ont pour objet des analyses d’ensemble, et voici, croyons-nous, celles qui sont les plus importantes. C’est tout d’abord un exposé schématique de la question de la variabilité des facteurs de production^[74], c’est-à-dire de la variabilité des quantités des différents éléments (matières premières ou services producteurs) susceptibles d’assurer l’obtention d’un produit déterminé, ainsi que la question subséquente du choix de l’affectation d’un élément quelconque à la fabrication de tel ou tel produit, question d’ailleurs traitée par M. F.-Y. Edgeworth, dès 1889 (Cf. infra, ch. III. § 2). C’est ensuite un examen général « à vol d’oiseau » du problème de la production et de l’échange en vue d’établir que ce problème est toujours parfaitement déterminé. C’est enfin l’étude de certains points de la théorie des monopoles, qui, en s’y prêtant tout particulièrement, a souvent inspiré des applications des mathématiques à l’économie politique. Mais même dans ces analyses d’ensemble, l’auteur des Principles s’est toujours borné adonner de simples indications, sans entrer dans une analyse approfondie.

⁂

Ce n’est pas uniquement dans ses Principles que M. Marshall a fait appel à l’emploi des graphiques ou des équations, mais comme cet ouvrage constitue la partie essentielle de son œuvre, nous croyons que les quelques considérations qui précèdent sont suffisantes pour préciser ses conceptions économico-mathématiques. Il ne faut d’ailleurs pas voir dans ces considérations une manifestation d’un esprit de dénigrement qui, à l’égard d’un auteur qui jouit d’une autorité indiscutée, serait aussi malséante que maladroite de notre part. Si nous avons cru devoir souligner que, tout compte fait, le professeur de Cambridge ne s’est guère écarté des routes classiques, c’est uniquement parce que certains détracteurs systématiques de l’emploi des mathématiques en économie politique prétendent donner son œuvre comme un exemple, absolument typique, de la faiblesse des ressources qu’un économiste avisé, fut-il doublé d’un mathématicien averti, peut trouver dans cette voie. Or, si M. Marhiall n’a rencontré qu’un médiocre concours dans l’emploi des mathématiques, c’est qu’il ne lui en a pas demandé un plus efficace parce qu’il n’a pas estimé qu’à côté de l’économie appliquée il y avait place pour l’économie pure. On ne saurait donc voir dans ses explications que la manifestation d’une simple opinion relative à la consistance de la science économique, sans pouvoir y trouver, ainsi que l’on a vainement tenté de le faire, une preuve irrécusable de la faillite de l’emploi des mathématiques dans son édification, sans compter qu’il serait quelque peu étrange de rechercher cette preuve chez un auteur qui se réclame lui-même des idées de Cournot et de von Thünen.

§ 4. — Léon Walras.

Tandis que Gossen et Jevons peuvent être considérés comme les fondateurs de l’économie pure, parce que, les premiers, ils ont établi le principe de l’utilité finale qui a fourni, non pas sans doute la charpente de cette science puisque, comme nous le verrons, M. Pareto est parvenu à l’en affranchir, mais du moins l’échafaudage qui a permis de l’édifier, Walras en est le véritable créateur, car c’est lui qui l’a construite et si solidement que, jusqu’à ces derniers temps, ses successeurs se sont bornés à en modifier l’aménagement intérieur sans avoir à retoucher le gros œuvre. L’œuvre économique de Walras n’est d’ailleurs pas limitée à l’économie pure, elle embrasse l’étude de toute la partie économique de la science sociale ; mais comme il a pris soin de diviser lui-même cette étude en trois parties, ayant respectivement pour objet l’économie politique pure, l’économie sociale et l’économie politique appliquée, il nous sera facile de ne pas sortir de notre sujet en ne nous arrêtant qu’aux travaux qui composent la première partie, la plus importante du reste, et qui ont pris un corps définitif dans la quatrième édition de ses Éléments d’économie politique pure ou théorie de la richesse sociale^[75].

À ne lire — ainsi que l’ont certainement fait quelques critiques — que la préface de cet ouvrage, dans laquelle l’économie pure est définie « la théorie de la détermination des prix sous un régime hypothétique de libre concurrence absolue », il semblerait que le professeur de Lausanne ait assigné à cette science des limites bien étroites. Mais ce n’est là qu’une apparence, car la mutuelle dépendance des facteurs économiques ne permettant pas de procéder correctement à cette détermination des prix sans tenir compte des autres éléments de l’équilibre, la mise en équation du seul problème qu’il s’est proposé a tout naturellement conduit Walras à écrire, dans le cas de la libre concurrence, les conditions générales de l’équilibre économique, conditions dont la découverte restera sa gloire^[76]. À vrai dire, la question de la détermination des prix est un véritable fil d’Ariane, que l’auteur des Éléments a offert à leurs lecteurs, car, en donnant un prétexte concret à la recherche des conditions de l’équilibre économique, elle permet d’aborder l’étude du cas général par l’examen d’un certain nombre de cas particuliers très simples, à travers lesquels le lecteur se trouve insensiblement conduit à envisager des abstractions qui, considérées de piano, auraient pu lui paraître aussi inextricables que dénuées de signification.

Voici, en effet, l’économie des Éléments d’économie politique pure de Walras.

Dans une première section, l’auteur commence par exposer sa conception de l’objet et des divisions de l’économie politique et sociale ; mais ce ne sont là que des considérations plus ou moins philosophiques sur lesquelles nous nous arrêterons d’autant moins que, dans sa constante préoccupation de préparer dans son économie pure la justification du système social qu’il entendait préconiser, le professeur de Lausanne a posé dans cette partie de son œuvre certains principes qui prêteraient à des confusions, si la belle ordonnance de ses idées positives ne venait remédier à ce qui pourrait sembler un peu confus dans l’exposé de ses conceptions métaphysiques.

C’est dans la seconde section que Walras entre dans son sujet proprement dit par l’exposition de sa théorie de l’échange de deux marchandises entre elles. Il a divisé la solution de cette question en deux parties. Évaluant le prix de chaque marchandise en prenant l’autre comme numéraire, il a commencé par montrer comment, étant donné deux marchandises, on peut déduire le prix « de l’une en l’autre » de la connaissance de leurs courbes de demande, puis il a établi que ces courbes de demande résultent elles-mêmes de l’utilité dé ces deux marchandises pour chacun des échangistes ainsi que de la quantité de chacune d’elles possédée par chacun des porteurs ; et il en a finalement conclu que « les prix d’équilibre sont égaux aux rapports des raretés [id est des degrés finaux d’utilité] »^[77]. Cette conclusion est foncièrement identique à celle à laquelle Jevons est arrivé par une voie différente. Cependant Walras ne s’est nullement inspiré des idées du professeur du Collège Owens, dont il ignora totalement les travaux économiques jusqu’au moment où, sa théorie publiée, M. d’Aulnis de Bourouill, alors étudiant à l’Université de Leyde, pais Jevons lui-même^[78], vinrent lui révéler la coïncidence des résultats auxquels il était parvenu avec ceux qu’avait obtenus son devancier. Le point de départ du Professeur de Lausanne fut uniquement son désir d’appliquer le calcul des fonctions indiqué par Cournot à une théorie de la valeur d’échange exposée par son père A.-A. Walras, dans un ouvrage intitulé : De la nature de la richesse et de l’origine de la valeur^[79]. Du reste, loin d’éprouver du dépit du fait de la découverte de la concordance de sa conclusion avec celle de Jevons, Walras vit au contraire avec satisfaction dans cette concordance une confirmation de ses principes. C’est ainsi qu’il fut le premier à proclamer^[80] la priorité de son prédécesseur, et cela d’autant plus volontiers qu’il conservait en propre les plus importantes de ses conceptions, car l’étude de l’échange, sur un marché ne comportant que deux marchandises, ne se présente dans les Éléments que comme préparation à l’exposition de celles qui figurent dans la troisième section.

Cette troisième section a pour sujet la théorie de l’échange d’un nombre quelconque de marchandises entre elles, théorie qui peut être considérée, à un double titre, comme la partie capitale de l’œuvre de Walras, car non seulement, ainsi que nous allons le voir, elle fournit la substratum de toutes les autres, mais encore elle présente la manifestation la plus caractéristique de cette mutuelle dépendance, dont le Professeur de Lausanne a eu l’honneur de signaler l’influence là où les économistes littéraires ne cherchaient que des rapports de cause à effet. Cette théorie est en effet l’exposé des conditions auxquelles doivent satisfaire les quantités de marchandises échangées sur un marché et les prix correspondants pour que l’équilibre puisse s’établir sur ce marché ; or, la seule existence de ces conditions, en montrant la solidarité des différents éléments de l’équilibre, établit d’une façon définitive l’inanité de toutes les recherches entreprises pour découvrir « la cause » du prix ou de la valeur. Comme nous aurons ultérieurement l’occasion d’indiquer en détail la consistance de l’œuvre de Walras, nous nous contenterons d’énoncer ici, sans commentaire, les conditions d’équilibre de l’échange. Ce sont : pour chaque individu, la réalisation du maximum de satisfaction correspondant à l’égalité des prix aux rapports des raretés (degrés finaux d’utilité) et l’équivalence de ses recettes et de ses dépenses, et, pour chaque marchandise, la compensation de l’offre et de la demande. Puis, pour en terminer avec la troisième section des Éléments, nous ajouterons simplement que l’auteur l’a complétée par une rapide esquisse monétaire qui l’a finalement amené à reprendre en considération les courbes de prix dont les équations, sous le nom d’équations de la demande ou du débit, avaient été posées a priori par Cournot.

La quatrième section vient en quelque sorte compléter la précédente, en ce sens qu’elle a pour objet la détermination de certaines inconnues précédemment considérées comme des données. Dans la troisième section, en effet, se préoccupant uniquement des prix des marchandises, Walras avait supposé préfixées les quantités qui en sont apportées sur le marché. Or, cette hypothèse ne peut être regardée que comme une première approximation par laquelle, fidèle à sa méthode consistant à « aller du simple au composé », l’auteur des Éléments a jugé bon de faire passer leurs- lecteurs, car il est bien évident que les quantités produites dépendent des prix de vente. Aussi, à la suite de sa théorie de l’échange, le professeur de Lausanne s’est-il préoccupé de déterminer ces quantités ou plutôt les relations qui les rattachent aux prix des marchandises ainsi, bien entendu, qu’aux prix et quantités des services producteurs (usage de la terre, du travail et du capital), et c’est là ce qui fait l’objet de la « théorie de la production » exposée dans la quatrième section. Il est parvenu ainsi à un système d’équations, en nombre égal à celui des variables, qu’il n’a envisagées qu’au point de vue de l’évaluation des prix des services producteurs parce que les questions de prix étaient les seules qu’il entendait résoudre, mais qui représentent en réalité les conditions générales de l’équilibre économique sous le régime de la libre concurrence, à savoir :

La réalisation de la satisfaction maximum pour chaque individu ;

La compensation des recettes et des dépenses de chaque individu ;

L’équivalence entre les quantités de services producteurs offertes et les quantités de services demandées ;

Enfin l’égalité des prix de revient et des prix de vente. Walras a d’ailleurs présenté cette théorie de la production très simplement, grâce à l’introduction dans son analyse d’un entrepreneur idéal se bornant à acheter des services producteurs et à vendre des produits, ce qui, lui a permis de scinder son étude en considérant séparément le marché des services et celui des produits, sans toutefois faire abstraction des phénomènes qui, en fait, rendent les deux marchés solidaires l’un de l’autre.

Après avoir établi les conditions d’équilibre de l’échange et de la production, Walras a exposé dans la cinquième section de son traité une théorie de la capitalisation, et dans la sixième une théorie de la monnaie. Mais nous ne nous arrêterons pas à ces deux dernières théories, parce que la capitalisation ne diffère pas, au point de vue strictement mathématique, de la détermination de l’équilibre de la fabrication de choses quelconques, et que la question de la monnaie sortirait du cadre que nous [nous sommes fixé^[81]. Signalons ce pendant que le professeur de Lausanne a insisté sur la variabilité du degré d’utilité de la monnaie, qui, lorsqu’elle a été négligée, a été la cause de graves erreurs connexes à cette confusion de la courbe de l’utilité avec celle des prix, que nous avons précédemment rencontrée dès l’apparition des graphiques en économie politique, dans les travaux de Dupuit.

Les Éléments se terminent par deux sections dans lesquelles les mathématiques ne jouent qu’un rôle tout à fait secondaire. La première intitulée Conditions et conséquences du progrès économique. Critiques des systèmes d’économie politique pure, comprend, comme son titre l’indique, deux parties : l’une, à tendances politiques, dans laquelle Walras s’est efforcé de poser les jalons de ses conceptions sociales ; l’autre, purement critique, consacrée à l’examen et à la réfutation de la doctrine des physiocrates et de théories anglaises du coût de la production, de la rente et des salaires. Quant à la seconde section, dans laquelle l’auteur des Éléments, qui ne s’était préoccupé jusque-là que de la libre concurrence, a abordé les questions des tarifs, du monopole et des impôts, elle n’offre guère qu’une reproduction des idées de Cournot — à cette différence près, qu’au lieu de passer du monopole à la concurrence indéfinie, le professeur de Lausanne a préféré, ainsi que nous l’avons vu à propos de la troisième section des Éléments, procéder dans l’ordre inverse — suivie de considérations sociales sur la répartition^[82].

Ayant ainsi indiqué la substance des Éléments, il ne nous reste plus à dire que quelques mots de leur composition.

Cette composition participe tout à la fois du désir d’offrir une étude aussi claire que possible — au risque de paraître long — des fondements de la science économique et de celui de faire aboutir cette étude à la justification de la supériorité pratique de la libre concurrence. Aussi présente-t-elle un curieux mélange de théories mathématiques et de considérations morales ou sociales — ou même métaphysiques — car l’auteur des Éléments n’est jamais parvenu, semble-t-il, à se libérer complètement de certaines préoccupations des économistes littéraires, telles, par exemple, que la recherche des causes lorsqu’il s’agit de phénomènes interdépendants.

Mais les digressions, encore qu’elles masquent parfois les résultats obtenus, n’ont nui en aucune mesure à l’édification régulière, qui s’est poursuivie normalement à côté d’elles, ou même malgré elles, de la théorie de l’économie pure. Walras ne s’est jamais cru lié dans ses développements par telle distinction entre l’art et la science établie au début de son ouvrage pour des raisons d’opportunité, et, à côté de la recherche de la cause de la valeur, il n’a pas hésité à montrer, le premier, la multiplicité des facteurs dont elle dépend. Son esprit hautement scientifique a toujours su dominer ses tendances pratiques, et c’est pour cette raison qu’il a laissé une œuvre dont, selon l’expression de l’un de ses critiques aussi sévère qu’autorisé, on peut dire, comme Napoléon de ses victoires : « Il y a là du solide que la dent de l’envie ne peut ronger ».

CHAPITRE III

Les principaux économistes mathématiciens.

§ 1. — Wilhelm Launhardt.

L’un des premiers disciples de Walras, et celui qui peut-être s’est le plus conformé à ses principes, tout au moins dans la première partie de son principal ouvrage, fut M. Wilhelm Launhardt, directeur de l’École supérieure technique de Hanovre, qui est d’ailleurs parfois parvenu à des conclusions diamétralement opposées à celles du professeur de Lausanne, ce qui n’est pas étonnant, étant donné que ces deux auteurs se sont bornés, pour résoudre des problèmes pratiques, à appliquer purement et simplement les résultats de leurs recherches scientifiques sans se préoccuper des facteurs, éthiques ou autres, qui ne figuraient pas dans leurs équations.

Dès 1872 M. Launhardt se préoccupa de l’application des mathématiques à la solution de questions économiques, et c’est ainsi qu’il publia successivement un ouvrage sur le tracécommercial des voies de communication^[83], un travail sur l’emplacement convenable pour un établissement industriel^[84], et, enfin, une étude sur des questions économiques relatives aux chemins de fer^[85]. Puis, sur ces entrefaites, il eut l’occasion de lire la Mathematische Theorie der Preisbestimmung der wirihschaftlichen Güter de Walras, publiée en allemand par Louis de Winterfeid^[86], et la Theory of political economy de Jevons, ce qui l’amena à écrire son principal ouvrage d’économie mathématique : Mathematische Begründimg der Volkswirthschaftslehre^[87].

Cet ouvrage comprend trois parties : l’échange, la production des marchandises, le transport des marchandises.

M. Launhardt a fait reposer sa théorie de l’échange sur les mêmes bases que Walras. Il en a simplement modifié très légèrement l’exposé, en substituant aux courbes (ou à leurs équations) représentant les variations du degré de l’utilité en fonction des quantités consommées, d’autres courbes (ou leurs équations) représentant les variations de l’utilité totale en fonction de ces mêmes quantités. Mais, tout en ayant adopté le même point de départ que le professeur de Lausanne, il a orienté ses recherches dans une direction toute différente de celle de son prédécesseur, ce qui s’explique sans doute par ce fait que, lors de la composition de sa Mathematische Begründung, l’économiste de Hanovre n’était en possession que de l’abrégé, traduit en allemand, des théories de Walras — il n’eut connaissance des Éléments qu’au moment de l’impression de son livre — et que dès lors il était amené à apporter dans le développement de ses théories le même esprit que celui qui avait présidé à la conception de ses travaux économiques antérieurs.

Tandis que le savant professeur de Lausanne s’est en général efforcé de présenter des synthèses d’ensemble du phénomène économique, M. Launhardt s’est au contraire arrêté à des analyses portant sur des points particuliers, analogues à celles que l’on rencontre constamment dans la science de l’ingénieur. Il est à cet égard un détail qui montre nettement que l’auteur de la Mathematische Begründung s’est fait une conception un peu étroite de l’emploi des mathématiques en économie politique : c’est la substitution d’équations particulières aux fonctions générales qu’on laisse figurer d’habitude dans les calculs d’analyse, l’adoption, par exemple, à l’instar de Gossen^[88], de l’équation d’une parabole comme fonction d’utilité (ou de satisfaction), ce qui non seulement diminue la généralité des théories, mais surtout donne à ces théories une précision purement gratuite qui conduit parfois à des conclusions erronées.

Quoiqu’il en soit, après avoir, comme nous l’avons dit, montré de la même manière que Walras comment le prix d’équilibre se trouve déterminé dans le cas de l’échange de deux produits entre deux individus, M. Launhardt a poursuivi l’étude de l’échange en calculant le profit que les deux échangistes sont susceptibles de recueillir. Il a été ainsi amené tout d’abord à constater que le libre jeu de l’offre et de la demande assure à ce profit sa valeur maximum ; mais ensuite il s’est aperçu que le profit total correspondant à une opération donnée pouvait être accru par le fractionnement de cette opération (Wiederholler Tausch), aussi a-t-il conclu de ses calculs au rejet définitif de la formule de l’école libérale « laisser faire, laisser passer », offrant de la sorte un exemple typique de la divergence (que nous avons signalée au début) de ses tendances pratiques et de celles de Walras.

L’exposé de la théorie de l’échange dans le cas particulier d’un marché ne comportant que deux échangistes ainsi terminé, M. Launhardt s’est, comme son prédécesseur, occupé de la généralisation de cette théorie en examinant d’abord le cas où le nombre des produits étant limité à deux, celui des échangistes est quelconque, puis celui où un nombre quelconque d’individus trafiquent sur un marché d’un nombre de produits également quelconque. Il est ensuite passé du problème de l’échange à ceux de l’achat et de la vente, par l’introduction dans son analyse de la monnaie, dont il s’est cru autorisé, pour plus de simplicité, à considérer l’évaluation comme une grandeur constante que, à défaut de mesure absolue, il a regardée comme égale à l’unité, rendant de la sorte les prix égaux aux degrés d’utilité des produits. Cette introduction de la monnaie l’a d’ailleurs conduit à faire entrer en ligne de compte pour la détermination des prix, la condition d’équilibre des budgets individuels (Gleichgewicht des Haushaltes).

Enfin, M. Launhardt a terminé la première partie de ton ouvrage en étudiant un certain nombre de questions particulières : la capitalisation, qu’il a traitée à un point de vue presque purement arithmétique ; l’influence sur les prix des frais généraux commerciaux (Handelskosten), qu’il a, à l’instar de Jevons, exprimée sous forme de réduction des quantités de produits obtenues dans l’échange ; les droits de douane, à propos desquels la spécialisation des données, et en particulier l’adoption d’une courbe d’utilité parabolique, l’a amené à énoncer cette règle assez inattendue : le meilleur droit de douane est égal au tiers de celui qui serait prohibitif ; la question classique des produits indivisibles, qu’il a du reste esquissée sans faire appel aux mathématiques.

Dans la seconde partie de sa Mathematische Begründung, qui a trait à la production, au lieu de continuer à s’inspirer des idées de Walras, M. Launhardt s’est plutôt inspiré des idées de Jevons. De même que l’économiste anglais, il a considéré la peine résultant du travail comme une satisfaction négative dont le degré d’intensité est fonction de la durée de ce travail, ce qui l’a tout naturellement conduit à représenter dans ses calculs la quantité de peine en fonction du temps par une expression parabolique, analogue à celle à laquelle il avait eu précédemment recours pour la satisfaction, et à poser le principe de l’égalité de prix du plaisir et de la peine, qui n’est autre chose que celui de l’égalité des degrés d’utilité des produits et de désutilité des travaux de production dont nous avons déjà eu l’occasion de parler. Il est à noter que dans son étude de la production. M. Launhardt s’est également attaché à mettre en évidence l’analogie entre le profit de l’entrepreneur et la rente du sol. Mais dans cette partie de son ouvrage, précisément sans doute sous l’influence de Jevons, il a donné, plus encore que dans sa théorie de l’échange, libre cours à sa tendance à fragmenter son analyse. Au lieu de réclamer des mathématiques le seul concours qui justifie entièrement leur usage en économie politique, en les utilisant à mettre en évidence la mutuelle dépendance des phénomènes économiques, qui ne peut se traduire que par des équations, il a limité leur emploi à l’établissement de formules, ainsi qu’avaient coutume de le faire les premiers, économistes mathématiciens. Par suite, cette étude de la production ne présente, à notre sens, qu’un intérêt restreint au point de vue scientifique.

Quant à l’étude des transports, qui fait l’objet de la dernière partie de la Mathematische Begründung son sujet est trop spécial et la façon dont il est traité trop particulière pour que nous songions à nous y arrêter dans un exposé aussi général que celui que nous essayons de faire. Elle participe du reste des mêmes tendances que le début de l’ouvrage.

Nous en resterons donc là de notre aperçu de l’œuvre économique de M. Launhardt, en rappelant toutefois qu’on lui doit en outre un travail sur la monnaie intitulé Das Wesen des Geldes^[89].

§ 2. — Francis Ysidro Edgeworth

En 1881, le professeur Francis-Ysidro Edgeworth, d’Oxford, a publié un volume intitulé Mathematical Psychics^[90]. Cet ouvrage, qui n’a pas uniquement pour objet l’économie politique, ne constitue pas, ainsi que l’indique son sous-titre An essai on the application of mathematics to the moral sciences, un traité proprement dit, c’est un simple exposé des idées de l’auteur. Il comprend deux parties. Dans la première, qui est théorique, le professeur d’Oxford pose les principes de l’usage des mathématiques dans l’étude des sciences morales en s’appliquant à en justifier l’emploi ; dans la seconde, qui est pratique, il fait l’application au calcul hédonistique des principes établis dans la première. Cette deuxième partie se subdivise elle-même en deux sections : l’une ayant trait au calcul économique, l’autre au calcul utilitaire. Et, tandis que le calcul économique a pour objet la recherche des conditions permettant à certaines personnes ou à certains groupements de personnes d’obtenir pour eux-mêmes le maximum d’utilité, le calcul utilitaire est relatif au contraire à la réalisation de la plus grande somme possible d’utilité pour une collectivité. Le livre est complété par plusieurs appendices théoriques ou critiques.

Depuis la publication de ce livre, économiste consommé et mathématicien distingué, M. Edgeworth a fait passer au crible de sa puissante analyse un grand nombre des travaux d’économie mathématique de divers auteurs. Il s’était déjà livré à des études critiques particulières, notamment sur la formule de l’échange de Jevons^[91] et sur la théorie de l’équilibre économique de Walras^[92], lorsque la brillante communication^[93] qu’il fit à la séance d’ouverture du Congrès de l’Association Britannique pour l’avancement des sciences, tenu à Newcastle en septembre 1889, le jeta définitivement dans la mêlée. C’est ainsi qu’il a dès lors publié de nombreux articles dans diverses revues parmi lesquelles nous citerons le Giornale degli Economisti et l’Economic Journal, organe de la Royal Economie Society, qu’il fonda en 1891 et dont il est le rédacteur en chef.

Mais ce serait cependant une erreur de croire que M. Edgeworth s’est borné à des critiques. Au contraire, il a introduit dans la science pure certaines notions qui sont restées à la base des œuvres les plus modernes, notamment la notion de dépendance des consommations d’où résulte le remplacement de la courbe de l’utilité par une surface dans le cas de deux biens, et par une variété de l’hyperespace dans le cas d’un plus grand nombre de biens (Cf. III, IV, 2 et 3). Et, en outre, il semble être le premier à avoir eu des idées d’ensemble sur le phénomène économique général non seulement sous un régime de libre concurrence absolue, mais aussi sous un régime de concurrence limitée ainsi que dans les divers cas de monopole^[94].

Dans l’étude de la libre concurrence absolue, partant de ce principe que la réalisation du maximum d’utilité possible pour chacun des contractants est à la base de toutes les transactions, M. Edgeworth a été naturellement amené à représenter l’équilibre de l’échange par des équations équivalentes à celles de Walras : par contre, ses conceptions relatives à l’équilibre économique général sont quelque peu différentes de celles du professeur de Lausanne en ce sens que, à côté de la concurrence commerciale, étudiée par Walras, il a envisagé ce que Cairnes a appelé^[95], par opposition à celle-ci, la concurrence industrielle.

Il existe en effet entre ces deux régimes une différence profonde, provenant de l’existence de cette sorte d’utilité négative de certains biens économiques, que Jevons a désignée sous le nom de désutilité (disutility)^[96]. Tandis que dans le cas de libre concurrence commerciale il n’y a pas lieu de se préoccuper des désutilités des quantités de produits qui entrent en jeu, parce qu’elles sont nécessairement égales aux utilités des produits reçus en échange, il n’en va pas de même dans le cas de la concurrence industrielle, où la désutilité d’un travail n’est nullement mesurée par l’utilité d’un service rendu.

Voici du reste, pour éclaircir ce point, la comparaison que M. Edgeworth a empruntée à M. Böhm-Bawerk^[97] en la généralisant : « Pour figurer les conditions possibles de la vie industrielle, représentons-nous un maître d’école sévère qui, pour développer chez ses écoliers la patience et la persévérance, leur distribue certains cadeaux — par exemple des jouets et des bonbons — en récompense d’une certaine fatigue on d’une certaine souffrance endurée. Ainsi le « coût » d’une bille sera d’écrire vingt lignes, le coût d’une toupie sera de rester une demi-heure en pénitence ».

« Supposons que la pratique de l’échange se répande dans cette jeune population, en supposant d’ailleurs la libre concurrence : il s’établira nécessairement un certain équilibre des échanges de telle façon que la valeur de chaque article corresponde à son utilité finale. C’est-à-dire que si une toupie s’échange contre dix billes, on peut en conclure que chaque garçon estime sa toupie autant que la dernière dizaine de billes qu’il a envie d’acheter. Ainsi l’utilité finale peut être regardée comme le principe régulateur. »

« Mais il est également vrai de dire que les désutilités des articles échangés sont égales. Si une toupie vaut dix billes, nous sommes autorisés à conclure que chaque enfant aime autant passer une demi-heure en pénitence que d’écrire deux cents lignes — coût de dix billes à raison de vingt lignes par bille ».

« Maintenant introduisons le principe de la division du travail, et supposons qu’il n’est pas permis à un même enfant d’apprendre à la fois le latin et le grec, mais qu’il a simplement la possibilité de choisir entre ces deux études. Cette hypothèse implique que les profits nets qui peuvent résulter de la production de vers grecs ou de vers latins dans chacun de ces départements de l’instruction sont équivalents. Supposons maintenant qu’une considération particulière ou un certain prestige ou quelque autre avantage qui ne résulte pas de l’échange direct des lignes écrites soit attaché à l’étude du grec. On pourra concevoir alors que vingt lignes de latin puissent avoir autant de valeur d’échange que cinquante lignes de grec, alors même qu’il serait beaucoup plus pénible pour un écolier d’avoir à écrire à la fin de sa tâche cinquante lignes de grec que vingt lignes de latin. En un mot, les avantages nets, les utilités totales de ces deux occupations qui consistent à écrire des vers latins ou des vers grecs sont égales. Mais les désutilités finales dans les deux départements de la production ne sont pas en général égales partout où prévaut la division du travail »^[98].

Par suite, dans le cas de concurrence industrielle, pour évaluer l’avantage qu’un individu tire des transformations économiques auxquelles il se livre, il faut tenir compte de la désutilité de ses efforts, en d’autres termes, l’utilité totale $\Phi$ qui résulte pour lui de ces transformations est fonction de son effort $e$. À cette nouvelle variable, introduite dans le système des équations de l’équilibre économique, correspond d’ailleurs une équation supplémentaire que l’on obtient en écrivant qu’au point d’équilibre cette fonction d’utilité $\Phi$ de $e$ est maximum, c’est-à-dire que sa dérivée totale par rapport à e est nulle. Il semblerait donc que le problème ne subisse pas du chef de la prise en considération de la désutilité des efforts une bien grande complication. Cette conception serait erronée. En effet, pour que l’équilibre économique s’établisse, il ne suffit pas que dans la catégorie de transformations auxquelles il se livre l’individu réalise le plus grand profit possible ; il faut encore que cette catégorie de transformations soit la plus avantageuse de celles qu’il lui est loisible de choisir, et à chacune desquelles correspond une forme particulière de la fonction d’utilité $\Phi$.

Dès lors, « si nous essayons maintenant de mettre en formule la concurrence industrielle, il convient de considérer les utilités dont on s’occupe, non plus simplement comme variant continuellement avec l’accroissement ou le décroissement de variables dont elles représentent une fonction constante, mais aussi comme variant d’une façon discontinue par suite de changement dans la fonction^[99]. Le problème n’est plus simplement de découvrir ce système de variables par lequel l’utilité de toutes les personnes que l’on considère se trouve au maximum (dans le sens technique de ce terme), mais de trouver telles fonctions et telles valeurs des variables pour lesquelles la formule ne donne pas seulement un maximum, mais la plus grande valeur possible. Par le fait, il y a toute la différence qui existe dans le calcul des variables entre les problèmes où l’on se propose de trouver un maximum et ceux où l’on se propose de trouver la plus grande valeur possible^[100]»^[101].

Si nous nous sommes arrêté un peu longuement sur cette question quelque peu subtile, c’est qu’elle a donné lieu à une polémique assez vive dont nous allons dire un mot. Après avoir exposé les considérations précédentes, le professeur d’Oxford avait en effet conclu en ces termes dans le discours cité : « Si nous passons aux complexités qui surgissent de la division du travail, le problème [de l’équilibre économique] cesse d’être un simple problème d’algèbre ou de géométrie. Et alors, fussions-nous même en possession des données numériques relatives aux motifs agissant sur chaque individu, on pourrait à peine concevoir qu’il soit possible de déduire a priori l’état d’équilibre auquel tendrait un système compliqué à ce point » et M. L. Bortkevitch crut alors devoir prendre la défense de Walras^[102]. Mais il ne semble pas que les deux économistes se soient nettement entendus. M. Bortkevitch paraît avoir considéré les observations du professeur d’Oxford comme une critique des équations de Walras^[103], tandis que M. Edge worth, s’efforçant dans son analyse de se rapprocher du phénomène concret, avait en vue la solution d’un problème différent de celui qui a été traité par le professeur de Lausanne, problème plus général, dont il se bornait d’ailleurs à indiquer l’existence. « Je ne ferai jamais », disait-il^[104], « un reproche à un économiste mathématicien de n’avoir pas formulé le problème de la concurrence industrielle. Les représentations abstraites se trouvent toujours en défaut pour représenter la réalité ».

D’autre part, dans l’étude des monopoles et de la concurrence limitée auxquels il a également étendu ses recherches, ainsi que nous l’avons ci-dessus mentionné, non seulement M. Edgeworth a repris et complété les théories de Cournot, relatives à l’exercice d’un monopole sur des tiers se faisant librement concurrence, en se préoccupant notamment de l’influence de l’accroissement de la demande sur le prix^[105], mais encore il a examiné, pour la première fois en pleine connaissance de cause, l’hypothèse dans laquelle deux individus (ou deux groupements d’individus) jouiraient d’un certain monopole par rapport à un même produit^[106] (Cf. III, V, 4 et 5). Il s’est en outre préoccupé de l’indétermination de la position de l’équilibre économique qui résulte de la présence vis-à-vis l’un de l’autre de deux monopoleurs, comme un syndicat de patrons et un syndicat d’ouvriers, par exemple^[107]. Plus généralement, après avoir montré ce qu’il faut entendre par marché parfait, il a pris en considération les différents cas où le marché est imparfait par suite du nombre limité des concurrents, de l’indivisibilité des produits, de l’existence d’ententes (combinations), d’unions (unionism), d’associations coopératives etc.^[108]. Il a fait ressortir que dans ces hypothèses, où aucune position d’équilibre stable n’est déterminée a prioiri, il doit y avoir un principe d’ajustement (principle of adjustement) procurant une base aux transactions. Et il a indiqué que ce principe peut être fourni soit par les conditions de l’équilibre, considéré comme le πρακτὸν ἀγαθὸν, qui se trouverait réalisé sous un régime de libre concurrence absolue — de même que dans les travaux à la mer le talus naturel d’un remblai de pierre peut offrir à l’ingénieur l’inclinaison-type à donner à son ouvrage^[109] — soit par les conditions de l’ « arrangement utilitaire » qui assurerait aux divers intéressés la plus grande somme d’utilité compatible avec les circonstances.

Enfin, dans la section de ses Mathematical Psychics consacrée au calcul utilitaire, M. Edgeworth a recherché, comme nous l’avons dit, les conditions de la réalisation de la plus grande somme possible d’utilité pour une collectivité. Dans cette recherche, posant en principe que le plaisir est mesurable, il a commencé, en présence de quantités de plaisir relatives à des individus différents, par admettre que tous les plaisirs sont commensurables^[110], puis, pour répondre au besoin d’une unité, il a considéré, avec le psychologue-physiologiste Wundt, comme assimilables les plus petites quantités de plaisir perceptibles^[111]. Et il a été amené de la sorte à formuler cette conclusion que le plus grand bonheur possible (pour une collectivité) est égal à la plus grande valeur possible de l’intégrale $\iiint dp\,dn\,dt$ (où $dp$ correspond à la plus petite quantité de plaisir perceptible, $dn$ à un individu sensible, $dt$ à un élément de temps), les limites de l’intégration par rapport au temps étant $0$ et $\infty$, le présent et l’avenir indéfiniment, et les autres limites étant des variables qu’il y a lieu de déterminer à l’aide du calcul des variations^[112].

Mais il semble que dans cette partie de son œuvre M. Edgeworth ait subi l’influence de Jevons, à qui le professeur Marshall a pu reprocher de créer une confusion entre le domaine de l’économique et celui de l’hédonique, et l’on comprend que de telles conceptions aient pu prêter aux critiques. « Il y a un point », dit à ce propos M. Irving Fisher^[113], « où, à ce qu’il me semble, l’auteur de ce livre vraiment fécond en idées s’est écarté du droit chemin. On a reproché aux économistes mathématiciens cette énigme : Qu’est-ce qu’une unité de plaisir ? Et M. Edgeworth, à la suite du psychologue-physiologiste Fechner, répond : « Les plus petites quantités de plaisir perceptibles sont assimilables ». J’ai toujours pensé que l’utilité doit être susceptible d’une définition qui la rattachée ses rapports avec les biens positifs on objectifs. Un physicien serait certainement dans l’erreur en définissant l’unité de force le minimum sensible de sensation musculaire… Cette introduction subreptice de la Psychologie dans l’Économique me semble inappropriée et défectueuse…Il en est résulté que « les mathématiques » ont été accusées de « restaurer les entités métaphysiques précédemment écartées »^[114]. Le professeur d’Oxford a d’ailleurs été le premier à avouer que, en la circonstance, il avait « abandonné la terra firma des analogies physiques »^[115], et il a rappelé lui-même, il est piquant de le noter, l’accusation précitée du D^r Ingram^[116].

Ajoutons que nous allons voir dans un prochain paragraphe comment le professeur Irving Fisher a su se mettre à l’abri de ses critiques, et que nous montrerons plus loin comment le professeur Vilfredo Pareto s’est définitivement libéré de la considération des quantités de plaisir.

§ 3. — Rudolf Auspitz et Richard Lieben.

À côté de l’ouvrage de M. Launhardt, il en est un autre, en langue allemande, que nous ne saurions passer sous silence. Il est intitulé Untersuchungen über die Theorie des Preises^[117] et est dû à la collaboration de deux économistes autrichiens MM. Rudolf Auspitz et Richard Lieben. De même que les Éléments de Walras, cet ouvrage a essentiellement pour objet, ainsi que son nom l’indique, la détermination des prix, et il repose tout entier sur le principe de l’égalité de la valeur d’échange à la valeur d’usage de la dernière parcelle échangée. Il se divise d’ailleurs en deux parties : le corps même du livre et les annexes, de chacune desquelles nous dirons successivement quelques mots.

Dans la première partie, exclusivement géométrique, MM. Auspitz et Lieben ont fait appel à un mode de représentation graphique, déjà employé par le professeur Marshall, consistant à adopter comme coordonnées des courbes de demande et d’offre les quantités des deux produits échangés : le quid et le pro quo, avec cette particularité que dans leur ouvrage l’un des deux produits, celui dont ils portent les quantités en ordonnées, est toujours le numéraire qu’ils ont jugé à propos d’introduire immédiatement dans leurs recherches. Ils ont en outre considéré l’évaluation individuelle du numéraire comme une grandeur constante que, à défaut de mesure absolue, ils ont regardée comme égale à l’unité, ce qui leur a permis de rapporter aux mêmes axes, d’une part, les courbes d’utilité et les courbes de demande, et, d’autre part, les courbes de coût de production — qui sont en quelque sorte des courbes d’utilité négative — et les courbes d’offre qu’ils en déduisent en assimilant tous les offreurs à des entrepreneurs. Dans les conditions que nous venons de définir, les courbes de demande sont d’ailleurs les dérivées des courbes d’utilité du type usité par M. Launhardt dans sa Mathematische Begründung der Volkswirtschaftslehre^[118] dont, pour cette raison notamment, nous avons cru devoir rapprocher les Untersuchungen, de même les courbes d’offre sont les dérivées des courbes de coût de production.

Cela étant, les deux économistes autrichiens ont commencé par indiquer les dispositions générales et les caractéristiques des courbes d’offre et de demande. Puis ils ont recherché dans quelles conditions l’individu, tant comme producteur que comme consommateur, peut réaliser la plus grande satisfaction possible. Enfin, ils ont examiné l’influence sur la détermination des prix de l’abandon de certaines hypothèses simplificatrices primitivement adoptées, et envisagé la question des monopoles ainsi que celle du commerce international, à propos de laquelle le mode de représentation graphique adopté par eux leur a permis de faire ressortir nettement dans quelles conditions une taxe à l’importation ou à l’exportation est susceptible de produire des résultats avantageux^[119].

Dans la seconde partie — les annexes — les auteurs ont fait une assez large part à l’emploi de l’analyse, ce qui leur a permis de pousser leurs recherches plus loin qu’ils ne l’avaient fait dans la première partie. C’est ainsi qu’après avoir établi les équations des courbes précédemment prises en considération, ils ont étudié les variations de la satisfaction et recherché les conditions de son maximum sans s’astreindre à la regarder comme une fonction d’une seule variable : la quantité de tel ou tel produit ; ils sont au contraire entrés largement dans la voie ouverte par M. Edgeworth en la considérant a priori comme une fonction de tous les facteurs intervenant dans l’équilibre économique, qu’ils ont d’ailleurs ramenée en dernière analyse à une fonction des prix et des quantités des produits dont trafique l’individu envisagé, et de la quantité de numéraire dont dispose cet individu. C’est ainsi également qu’ils ont étudié les variations de la satisfaction indépendamment de l’hypothèse de la fixité de l’évaluation du numéraire, ce qui les a conduits, pour représenter ces variations, à remplacer les courbes par des surfaces de satisfaction (Befriedigungsflächen) analogues à celles que le professeur d’Oxford avait précédemment prises en considération, et sur lesquelles nous aurons l’occasion de revenir dans la troisième partie de ce travail (III, IV, 2). C’est ainsi enfin qu’ils ont pu déterminer les conditions générales de l’équilibre économique sans s’assujettir à supposer les prix indépendants les uns des autres, comme ils avaient cru^[120] indispensable de l’admettre dans un exposé géométrique.

Telle est dans les grandes lignes la structure générale des Untersuchungen. Nous ne croyons pas qu’il y ait lieu d’en faire une analyse plus détaillée parce qu’il ne nous semble pas qu’elles aient sensiblement modifié, par la contribution qu’elles lui ont apportée, le domaine de la science tel qu’il était constitué lors de leur publication, encore que MM. Auspitz et Lieben n’aient pas jugé à propos de donner d’indications bibliographiques sur les sources auxquelles ils ont puisé, sous le prétexte que si le lecteur est au courant des questions traitées, ces indications lui seraient superflues, et que si au contraire il n’est pas au courant, elles ne lui offriraient aucun renseignement qu’il ne puisse trouver dans tout livre d’étude détaillé. Dans tous les cas, en présence du développement considérable de leur ouvrage, on est tenté d’appliquer aux deux économistes autrichiens le reproche que M. Edgeworth adressa à un auteur qui avait pourtant le mérite d’apporter des innovations extrêmement importantes « It is true that we fin in him rather multum than multa ; that his principal achievement is the copious exposition of the one fondamental theorem we are referred [à savoir que la valeur d’échange est égale à la valeur d’usage de la dernière parcelle échangée] ». Or, d’une part, il est incontestable qu’il n’est pas dénué de danger de multiplier sans nécessité les développements mathématiques car, selon l’heureuse comparaison du professeur d’Oxford, ce mode de culture de la science, au lieu de favoriser la croissance des fruits de la vérité économique, a plutôt pour effet de fournir, à leurs dépens, un exubérant feuillage mathématique susceptible de les masquer, le cas échéant. D’autre part, il est fort à craindre que des applications trop laborieuses de la méthode mathématique ne soient préjudiciables à son emploi en économie politique, du fait qu’elles peuvent jeter le doute dans l’esprit de ceux à qui ce mode de raisonnement n’est pas familier en leur donnant à penser que les économistes mathématiciens ont pris pour devise : Odi profamum valgus et arceo. Il suffit pour s’en convaincre de se reporter au grand traité de M. Paul Leroy-Beaulieu, dans lequel, après avoir systématiquement critiqué l’usage des mathématiques en économie politique, l’auteur ajoute à titre de justification : « En écrivant ces lignes, nous avons sous les yeux deux tentatives d’applications de ce genre. La première consiste en un très volumineux et superbe traité allemand : Untersuchungen über die Théorie des Preises (Recherches sur la théorie des prix) par MM. Rudolf Auspitz et Richard Lieben [Leipsig verlag von Duncker et Humblot, 1889]. Il y a étonnamment d’ingéniosité et de science dépensées dans ce gros volume qui foisonne de figures géométriques et algébriques très compliquées. On y étudie successivement la courbe de l’utilité, celle des frais de production (die Kurven der Nützlichkeit, der Herstellungs kosten, etc.), leur concavité, leur convexité (Konvexität jeder Kurve, Konkavität jeder Kurve) les contre-courbures, etc, (Gegenkrümmungen) : tout cela et toutes ces combinaisons se poursuivent pendant 555 pages.

« Nous rendons justice à toute la patience et à toute la subtilité des auteurs qui se réfèrent pour l’établissement de leur théorie à Jevons, à Walras et aussi à l’école psychologique autrichienne. Nous sommes fâché d’être obligé de dire que, à notre sens, il n’y a aucun enseignement à tirer de semblables grimoires »^[121].

Pour en terminer avec l’œuvre de MM. Auspitz et Lieben, il nous faut signaler une polémique qui s’est élevée à son occasion entre ses auteurs et Walras. Dans la préface de leur ouvrage, les deux économistes autrichiens, faute d’avoir prêté une attention suffisante à ce fait que la théorie géométrique de l’échange de Walras était limitée à un marché ne comportant que deux produits, n’ont pas craint de prétendre que le professeur de Lausanne faisait appel à des hypothèses contradictoires ; celui-ci leur répondit en publiant dans la Revue d’Économie politique^[122], sous forme de bulletin bibliographique, une série d’« observations » sur les Untersuchungen que MM. Auspitz et Lieben entreprirent de réfuter point par point en une longue lettre adressée également à la Revue d’Économie politique^[123].

Le premier et même le second chef de cette discussion, relatifs à la supériorité de tel ou tel système de coordonnées et à l’opportunité de l’introduction plus ou moins rapide du numéraire dans la théorie de l’échange, ne sont guère que des disputes sur la pointe d’une aiguille, des questioni di lana caprina, selon l’expression de M. V. Pareto.

Le troisième et le cinquième chefs sont plus sérieux : ils ont trait à l’hypothèse de l’indépendance des prix, mais ils ont perdu beaucoup de leur importance depuis que Walras est parvenu à élaborer un exposé géométrique de toute la théorie économique indépendamment de cette hypothèse.

Le quatrième chef vise une accusation portée par Walras contre MM. Auspitz et Lieben d’être « tombés dans l’erreur de Dupuit » (II, I, 2), mais cette accusation semble être le résultat d’un simple malentendu de la part du professeur de Lausanne, qui n’a peut-être pas suffisamment tenu compte des conditions, qu’elles soient admissibles ou non, dans lesquelles se sont placés les deux économistes autrichiens.

Enfin, le sixième et le septième chefs portent sur le principe de l’égalité du coût de production et du prix de vente, qui fera l’objet d’un examen particulier dans la troisième partie de ce travail.

Nous ne nous occuperons pas davantage de cette polémique parce que, ne présentant pas de caractères de généralité et n’ayant pas eu d’influence sensible sur l’évolution de la science, elle n’offre plus aujourd’hui qu’un intérêt relatif, et que d’ailleurs, à l’époque où elle était d’actualité, elle a été analysée avec le plus grand soin par M. V. Pareto en une étude^[124] à laquelle il est toujours loisible de se reporter.

§ 4. — Irving Fisher.

Tant au point de vue de l’ordre chronologique qu’à celui de l’enchaînement des conceptions de l’économie mathématique, il convient de parler maintenant de la contribution que M. Irving Fisher, professeur à l’Université de Yale, a apportée à la science pure. Dans sa remarquable étude intitulée Mathematical investigations in the theory of value and prices^[125], il a, en effet, tout en faisant état des travaux de ses prédécesseurs, notamment de ceux de Jevons et de MM. Auspitz et Lieben, posé les principes ou du moins fourni les germes des théories les plus récentes.

Dans la première partie de cet ouvrage, l’auteur a commencé par remarquer que les théories des économistes mathématiciens qui l’ont précédé présentent un point faible, car ces économistes « omettent d’indiquer en quoi que ce soit ce qu’ils entendent par le rapport de deux utilités »^[126], alors que les graphiques auxquels chacun d’eux a recours participent de cette notion. On reconnaît, sous une forme légèrement différente, la critique que nous avons développée à propos de Walras, attendu que mesurer une quantité c’est précisément chercher un rapport : le rapport entre cette quantité et une autre choisie pour unité. En dernière analyse, c’est toujours la question de l’unité de plaisir qui se pose ; il s’agit de définir un étalon qui permette de mesurer le plaisir. Nous avons montré précédemment que cette question a été abordée par M. Edgeworth dans le cas où les intérêts d’individus différents sont simultanément en jeu, parce qu’alors il n’est pas possible de la passer sous silence, mais il est clair qu’il y a également lieu de lui donner une solution lorsque ne sont en jeu que les intérêts d’un seul individu, dès l’instant où — ce qui n’est nullement indispensable (III, V, 1) — l’on prend en considération des quantités de plaisir.

Nous avons vu à propos des Mathematical Psychics que la définition psychologique, proposée par le professeur d’Oxford, n’était pas de nature à donner satisfaction à M. Irving Fisher. Il y a en effet lieu de faire une distinction essentielle entre la psychologie et l’économie politique : tandis que la première de ces deux sciences étudie des sensations, la seconde a pour objet des phénomènes objectifs, d’où il résulte qu’elle comporte des définitions en relation avec des données positives. Aussi estimant que si Gossen et Jevons avaient considéré le calcul du plaisir et de la peine comme une partie fondamentale de leurs théories, c’est qu’ils n’avaient pas trouvé le moyen d’échapper à son emploi, le professeur de Yale s’est-il efforcé de débarrasser l’économie pure de toute considération subjective.

Il a commencé par poser ce postulatum conforme à l’hypothèse hédonistique : « Chaque individu agit suivant ses goûts »^[127], puis il a énoncé les trois définitions suivantes, afin de préciser le sens dans lequel l’utilité est une quantité :

I. — « Pour un individu donné, à un instant donné, l’utilité de A unités d’un produit ou d’un service (a) est égale à l’utilité de B unités d’un autre produit ou service (b), si l’individu ne désire pas l’un à l’exclusion de l’autre. »

II. — « Pour un individu donné, à un instant donné, l’utilité de A unités de (a) excède l’utilité de B unités de (b), si l’individu préfère (ou désire) A à l’exclusion de B plutôt que B à l’exclusion de A. Dans ce cas, l’utilité de B est dite moindre que l’utilité de A. »

III. — « Le rapport de deux utilités est mesuré par le rapport de deux accroissements infiniment petits du produit dont il s’agit, tels que leurs utilités soient respectivement égales à celles dont on cherche le rapport, pourvu que ces accroissements infiniment petits s’ajoutent à des quantités finies égales. »

« Cette définition s’applique non seulement aux utilités infinitésimales d’un même produit, mais aussi à celles de produits ou services différents. »

(M. Irving Fisher fait remarquer que cette dernière définition est absolument conforme aux autres définitions mathématiques.)

Dans ces conditions, l’utilité marginale (finale) d’un produit étant la limite du rapport de l’utilité d’un accroissement marginal à la grandeur de cet accroissement, on voit que le rapport de deux utilités marginales est le rapport des utilités de deux accroissements marginaux divisé par le rapport de ces accroissements. Dès lors « l’utilité marginale d’un produit, arbitrairement choisi, sur la limite (margin) d’une quantité arbitrairement choisie de ce produit peut servir d’unité d’utilité pour un individu donné à un instant donné. Cette unité peut être appelée un util ».

Par suite, en partant de ces définitions, il est facile de justifier, en précisant sa signification, la courbe de l’utilité de Jevons et par conséquent les œuvres de divers auteurs qui l’ont, plus ou moins directement, prise en considération. Et en fait, dans le cas de la libre concurrence, le seul dont il se soit occupé, M. Irving Fisher est parvenu à des équations qui sont essentiellement celles de Walras. Les seules différences fondamentales que l’on constate entre elles proviennent de ce que le docteur Irving Fisher a constamment fait figurer dans ses relations l’utilité marginale considérée comme une fonction des quantités de produits, tandis que le professeur de Lausanne avait regardé la quantité de chaque produit comme une fonction du prix. — Notons en passant que ce fait « que des résultats similaires aient été obtenus séparément et par des voies différentes, constitue certainement un argument à faire entrer en ligne de compte pour ceux qui se montrent sceptiques au sujet de l’emploi de la méthode mathématique »^[128]

Dans cette partie de ses Mathematical investigations, au lieu d’éclairer son exposé à l’aide de diagrammes, le professeur de Yale a préféré faire appel à des analogies mécaniques, parce que « ceux qui étudient l’économique sont naturellement portés à faire état de la mécanique plutôt que de la géométrie », et qu’ainsi « une illustration mécanique s’adapte plus parfaitement à leurs connaissances antérieures qu’une illustration graphique »^[129]. C’est ainsi qu’il a non seulement imaginé, mais encore fait construire un appareil^[130] qui rend en quelque sorte tangible la mutuelle dépendance des variables économiques, en montrant, grâce à un mécanisme ingénieux, le système économique en action, ainsi que l’a rappelé M. Pantaleoni au Congrès de Parme en septembre 1907^[131]. « Cet appareil ne constitue pas une simple merveille scientifique ; ce n’est pas seulement un procédé pratique d’illustration des systèmes d’équations auxquels… recourt l’économie mathématique : c’est, à proprement parler, un véritable instrument d’investigation, qui est susceptible de faire voir avec une singulière netteté quels seraient, cœleris paribus, les effets de telle ou telle cause, et à en donner une mesure approximative »^[132]. Les Mathematical investigations — qui n’ont d’ailleurs malheureusement pas été traduites en français — étant devenues introuvables en librairie et ne figurant que dans un très petit nombre de bibliothèques, nous donnerons, avec des figures, dans la quatrième partie de notre étude, une description détaillée de cet appareil présentant l’immense avantage de faire saisir, pour ainsi dire sur le vif, la consistance générale de l’équilibre économique, qui peut, dans une certaine mesure, se trouver masquée par des abstractions qui ne sont pas toujours faciles à saisir pour ceux qui ne sont pas familiarisés avec l’emploi des mathématiques.

Tandis que dans la première partie de son ouvrage, M. Irving Fisher avait admis avec Jevons, Walras, etc., que l’utilité de chaque produit ne dépend que de la quantité de ce produit, dans la seconde, au contraire, il a considéré l’utilité de chaque produit comme une fonction des quantités de tous les autres produits, par suite de l’existence de produits complémentaires (completing commodities) et de produits substituables — succédanés — (competing commodilies).

Ainsi que nous l’avons mentionné, le professeur Edgeworth, puis MM. Auspitz et Lieben s’étaient déjà arrêtés à cette conception, mais il faut remarquer que, d’une part, M. Irving Fisher n’eut connaissance des Mathematical Psychics qu’après l’achèvement de la seconde partie de son travail^[133], et que, d’autre part, il a donné à la théorie de la mutuelle dépendance des consommations un développement et une importance qu’elle n’avait pas dans l’œuvre du professeur d’Oxford, ainsi qu’il résulte du compte rendu des Mathematical investigations publié par ce dernier lui-même dans l’Economic Journal^[134]. Il est d’ailleurs digne d’être noté que M. Irving Fisher a reconnu^[135], à la suite du professeur Marshall^[136], que l’approximation obtenue grâce à l’hypothèse simplificatrice admise par ses prédécesseurs est en général suffisante, et qu’il n’a étudié le phénomène complexe qu’en tant que seconde approximation, de telle sorte qu’on ne serait pas fondé à lui reprocher d’avoir voulu aborder un problème trop compliqué dans l’état actuel de la science.

Dans cette seconde partie de son ouvrage, le professeur de Yale a été amené à faire une observation de la plus haute importance au point de vue des principes de l’économie pure. D’après ce que nous venons de voir, il avait fait reposer toutes ses recherches relatives à la théorie de la valeur et des prix sur trois définitions que nous avons rappelées. Or, il est évident que la définition III du rapport de deux utilités n’aurait plus aucun sens dès l’instant où il s’agirait de comparer des utilités relatives à deux individus différents. Eh bien ! non seulement M. Irving Fisher a fait remarquer, pour la première fois croyons-nous, que « dans le but d’étudier les prix et la distribution, il n’est pas nécessaire de préciser la signification du rapport d’utilités relatives à deux individus différents », mais encore il a fait observer que la définition III n’est nullement requise par la recherche de l’équilibre économique, à la condition de ne pas avoir recours aux systèmes de coordonnées employés par Gossen, Jevons, MM. Launhardt et Marshall, mais de partir de la notion de courbe d’indifférence (Cf. III, IV, 2) introduite dans la science par M. Edgeworth. Et c’est là une observation que nous retrouverons à la base des plus objectifs, et, par suite, des plus scientifiques des travaux d’économie pure, dus au professeur Vilfredo Pareto.

En outre de ses Mathematical Investigations et de divers ouvrages, notamment ses Elementary principles of economics^[137], contenant trop peu d’applications des procédés mathématiques pour que nous nous y arrêtions ici, on doit également à M. Irving Fisher A brief introduction to the infinitesimal calculus, designed especially to aid in reading mathematical economics and statistics^[138], ainsi qu’un grand nombre d’articles portant principalement sur des questions monétaires^[139].

§ 5. — Vilfredo Pareto.

L’œuvre économique du professeur Vilfredo Pareto peut être divisée en deux parties assez nettement distinctes. Elle comprend, d’une part, l’ensemble de ses travaux antérieurs à 1898, parmi lesquels il faut citer en première ligne son Cours d’économie politique professé à l’Université de Lausanne^[140], et, d’autre part, ses travaux postérieurs à 1898, principalement son Manuale di economia politica con una introduzione alla scienza sociale^[141] et son Manuel d’économie politique^[142][143].

⁂

Disciple de Walras et son successeur dans la chaire d’Économie Nationale de l’Université de Lausanne, M. Pareto a commencé par reprendre les théories de son prédécesseur pour en généraliser les conclusions, en complétant certaines données, et en étendre le domaine.

Il y a cependant entre les Éléments de Walras et le Cours de M. Pareto des différences profondes du fait que les deux auteurs ont eu en vue des objets tout différents.

Le premier poursuivait un but pratique : démontrer l’excellence de sa doctrine. Il n’a par suite fait l’étude que du seul régime économique qu’il avait dès lors à prendre en considération, celui de la libre concurrence. « L’économie politique pure est essentiellement la théorie de la détermination des prix sous un régime hypothétique de libre concurrence absolue »^[144]. Il a d’ailleurs été amené, pour atteindre son but, à faire intervenir certaines considérations métaphysiques.

Le second, au contraire, s’est proposé de traiter l’économique à un point de vue purement scientifique, de telle sorte qu’il a été naturellement conduit à examiner, à côté de la libre concurrence, les divers types de monopole, parmi lesquels il faut ranger les régimes socialistes. En outre, dégagé de tendances pratiques, il s’est efforcé de prendre une position aussi objective que possible pour faire de l’économie pure, débarrassée de toutes conceptions philosophiques, la première approximation dans l’étude du phénomène économique concret.

Le Cours de M. Pareto se compose de deux sections : l’économie pure et l’économie appliquée, deuxième approximation dans la recherche des conditions de l’équilibre économique. En effet, « deux conceptions dominent tout ce livre : celle des approximations successives et celle de la mutuelle dépendance, non seulement des phénomènes économiques, mais aussi des phénomènes sociaux »^[145].

La première section (économie pure) comprend l’exposé des conditions générales de l’équilibre économique, non seulement dans le cas de la libre concurrence, dans lequel l’individu accepte les prix du marché sans essayer de les modifier directement et volontairement, mais aussi, d’après ce que nous venons de dire, dans le cas où un individu ou une collectivité, jouissant à quelque titre que ce soit d’un monopole quelconque, — c’est-à-dire d’un avantage spécial sur les autres individus justifiant l’espoir du succès — s’efforce, en réglant son offre et sa demande, de dominer le phénomène économique pour modifier les prix dans son intérêt ou dans tout autre but, tout en faisant état des conditions du marché. Cette étude de l’équilibre économique, dans laquelle M. Pareto distingue des positions stables et des positions instables, se divise en deux parties : l’étude de l’échange correspondant aux transformations économiques, et l’étude de la production correspondant aux transformations matérielles (Cf. infra III, V, 3). Nous retrouvons ainsi les deux problèmes envisagés par Walras.

Bien que dans tout cet exposé, M. Pareto se soit, en général, placé dans les mêmes conditions restrictives que Walras, et qu’il ait admis les mêmes hypothèse simplificatrices, il a néanmoins introduit certaines conceptions nouvelles qui ont assuré une plus grande généralité à sa théorie cependant que l’emploi de l’analyse^[146] permettait de lui donner une plus grande extension. C’est ainsi que prenant en considération, avec les professeurs Edgeworth et Irving Fisher (Cf., supra §§ 2 et 4) ce fait que l’ophélimité (utilité) procurée par la consommation d’une marchandise dépend fréquemment de la consommation d’autres marchandises, il a été amené à distinguer plusieurs espèces de dépendances : d’une part, celles qui correspondent à l’existence de succédanés, et, d’autre part, celles qui proviennent de ce que certains biens nous procurent plus de plaisir réunis que séparés, soit parce qu’ils se complètent, soit parce que par suite de leur réunion nos dispositions se trouvent modifiées, (si bien que le plaisir total procuré par plusieurs consommations peut être influencé par leur ordre^[147]). Dans la même partie, après avoir montré mathématiquement la décroissance de la demande en fonction du prix, M. Pareto s’est de plus préoccupé des exceptions à cette décroissance provenant de l’existence de succédanés. Cette étude de la dépendance des consommations a d’ailleurs permis au professeur de Lausanne d’expliquer un phénomène qui semble a priori paradoxal : dans les années de famine, la demande du pain augmente au lieu de diminuer avec la cherté du prix. « Il semble », dit Malthus^[148], « que l’on n’ait pas assez fait attention à une cause particulière de la cherté. Le prix du blé en temps de rareté dépend beaucoup moins du déficit réel que de l’espèce d’obstination avec laquelle on persiste à vouloir soutenir la consommation au même degré ». M. Pareto remarque^[149] que cette prétendue obstination provient de ce que les classes pauvres sont peu à peu obligées, à mesure que les prix s’élèvent, de renoncer à certains aliments de qualité supérieure et de se contenter de pain, dont, par suite, la consommation augmente.

Dans cette première section du Cours, les démonstrations mathématiques ont une importance fondamentale, quoique, par suite des nécessités didactiques inhérentes à un cours destiné à des étudiants en droit, l’auteur ait dû les placer en notes. Dans la deuxième section (économie appliquée) l’emploi des mathématiques ne joue au contraire qu’un rôle très secondaire, sauf lorsque l’auteur traite de sujets particuliers tels que : la question de la répartition des revenus, la théorie de la monnaie (analogue à celle de Walras), la théorie de la rente, qui vient réfuter celle de Ricardo. M. Pareto, en effet, s’est servi, sans aucun parti pris, de tous les moyens qui lui ont semblé propres à la découverte de la vérité, et c’est à tort qu’on le considère parfois comme un auteur qui veut appliquer les mathématiques à l’économie politique de préférence à toute autre méthode. « Lorsque nous avons rencontré quelque fait historique intéressant l’économie politique, nous n’avons pas craint de nous livrer aux recherches critiques qui pouvaient donner à ce fait une vraie valeur. Enfin, lorsque nous avons eu à traiter de l’évolution, nous n’avons pas hésité à emprunter des notions de fait et des explications aux sciences biologiques »^[150].

Nous sortirions de notre programme en nous arrêtant longuement sur cette seconde section, étant donné que l’emploi des mathématiques y est relégué au second plan. Qu’il nous suffise de dire que la théorie qui y est exposée se rapproche de la réalité en tenant compte de certains éléments perturbateurs négligés tout d’abord, en tenant compte, par exemple, dans l’étude de la production, de la variabilité des coefficients de fabrication quantités des services producteurs qu’il est nécessaire d’employer pour obtenir une unité de produit) que Walras avait considérés comme constants. Mais ce n’est encore là qu’une seconde approximation, car il s’agit toujours d’états limites ; il ne saurait être question de faire une description du phénomène économique concret qui est du domaine de la sociologie (Cf. I, II, 3).

Tels sont, dans les grandes lignes, les caractères du Cours qui est complété par de nombreuses études historiques et statistiques. « No other work contains such a compact, varied and comprehensive collection of statistical data » (Irving Fisher, Yale Review). Nous n’insisterons pas davantage sur cet ouvrage, parce que nous aurons l’occasion d’en revoir les éléments à propos du Manuel, dans lequel nous trouverons les idées actuelles du Maître sur l’économie politique.

⁂

À partir de 1898 M. Pareto s’est avisé que pour déterminer l’équilibre économique, il n’est nullement besoin de connaître la mesure du plaisir, un indice du plaisir suffit. C’est là l’origine de la théorie qu’il a commencé à exposer dès cette époque, qu’il a ensuite développée dans son Manuale, et qu’il a enfin présentée dans toute sa généralité dans son Manuel. Graduellement (Cf. III, V, 1 et 2), se dégageant des conceptions de l’ancienne économie politique, à la notion d’ophélimité il a substitué celle de fonction-indice, assez analogue à la notion de température (Cf. p. 175 n.), et le Manuel a dans une certaine mesure pour objet d’édifier la théorie de l’équilibre économique indépendamment de l’hypothèse de Walras et de « la condition de satisfaction maximum », sur laquelle reposait encore le Cours. L’utilité des dernières parcelles échangées, la rareté, le plaisir, l’ophélimité qui, en toute rigueur, ne peuvent être considérés comme des quantités ni, par suite, être soumis à l’analyse mathématique, ne figurent plus dans les équations du Manuel.

Nous aurons, dans la III^e partie, l’occasion d’insister sur ce sujet, qui n’est d’ailleurs pas du domaine de l’histoire ; nous nous bornerons donc ici à exposer quelques-unes des idées directrices qui sont à la base des dernières œuvres de M. Pareto.

D’une façon générale, dans le Manuale et dans le Manuel, l’auteur s’est efforcé d’affirmer la position objective qu’il avait prise dans le Cours : tandis que dans les déductions pratiques qu’il tirait de la théorie du Cours, il ne cachait nullement ses tendances libérales, — sans que toutefois cette théorie ait pour objet de démontrer la supériorité de telle doctrine considérée comme orthodoxe — il s’est placé dans le Manuel au point de vue de la science pure, sans laisser aucune place à l’art. Par suite, il a cherché à accroître la généralité de ses théories en les débarrassant de tout ce qui était susceptible, en apparence ou en fait, de les rapprocher de réalités nécessairement particulières et subjectives, et en ne prenant en considération que des phénomènes moyens : « Nous étudierons les actions logiques^[151], répétées, en grand nombre, qu’exécutent les hommes pour se procurer les choses qui satisfont leurs goûts »^[152].

C’est ainsi que dans le Manuale et ensuite dans le Manuel, au lieu de commencer par prendre séparément en considération l’échange et la production, le professeur de Lausanne étudie immédiatement l’équilibre économique en général, en le regardant comme naissant dans son ensemble du contraste des goûts des hommes et des obstacles que rencontre leur satisfaction, et que, plus tard, dans l’Encyclopédie des sciences mathématiques pures et appliquées^[153], il a été encore plus loin en faisant abstraction des obstacles eux-mêmes, pour ne tenir compte que des différents genres de liaisons qui peuvent en résulter, liaisons qui constituent, à proprement parler, les liens de mutuelle dépendance du système économique.

C’est ainsi également que dans le Manuel, au lieu de parler des phénomènes économiques des types concrets nécessairement un peu vagues : libre concurrence, monopoles, etc., M. Pareto considère les phénomènes de trois types abstraits à caractéristiques mathématiques rigoureusement déterminables. Si l’individu accepte les prix du marché en se laissant uniquement guider par ses goûts, on a le type 1 (libre concurrence). Si, au contraire, il cherche à modifier les conditions du marché, dans son intérêt ou dans tout autre but, on a le type II (monopole pouvant d’ailleurs être exercé par un groupement)^[154]. Enfin, le type III « est celui auquel on arrive quand on veut organiser tout l’ensemble du phénomène économique, de telle sorte qu’il procure le maximum de bien-être à tous ceux qui y participent… Le type III correspond à l’organisation collectiviste de la société »^[155]. Sous ces formes, les divers cas de monopole qui n’étaient abordés qu’accessoirement dans le Cours sont définitivement incorporés dans l’étude de l’équilibre économique au même titre que la libre concurrence.

Ajoutons que M. Pareto ne s’est pas borné à renouveler les dispositions d’ensemble de ses premiers travaux, il a aussi apporté sur certains points particuliers des modifications profondes, qui participent de la même tendance à généraliser en simplifiant. Dans ses derniers ouvrages, par exemple, il ne considère plus la notion de capital comme fondamentale. « Au point de vue strictement mathématique de la détermination de l’équilibre, la capitalisation ne diffère pas de la fabrication de choses quelconques »^[156], (elle constitue en somme les premiers échelons de la production.)

Le Manuel est complété par des études d’économie appliquée sur la population et sur les capitaux fonciers et les capitaux mobiliers, et enfin par un aperçu d’ensemble du phénomène économique concret. Ces derniers chapitres mettent nettement en évidence l’importance du rôle de l’économie pure, en offrant à une étude générale des bases réellement scientifiques, qui permettent de la soustraire aux influences éthico-métaphysiques.

Nous nous sommes efforcé dans ce qui précède de donner une idée d’ensemble de l’œuvre actuelle de M. Pareto. Nous essaierons dans la III^e partie de faire voir plus clairement les résultats qu’il a obtenus, mais nous croyons devoir dès à présent souligner que cette œuvre vaut non seulement par ces résultats, mais encore par ceux qu’elle permettra d’obtenir grâce aux éléments qu’elle a fournis à la science. Le savant professeur de Lausanne a commencé à frayer une voie nouvelle qui ne saurait manquer d’être féconde, car on y découvre dès à présent de nombreux problèmes, dont les ἀγεωμετρητοί ne soupçonnaient même pas l’existence et dont la solution n’est encore actuellement qu’effleurée (Cf. Pareto, passim).

CHAPITRE IV

Indications bibliographiques.

Nous ne saurions avoir la prétention de passer en revue tous les auteurs qui se sont occupés peu ou beaucoup d’économie mathématique, car nombreux sont ceux qui, depuis une quarantaine d’années surtout, ont fait dans leurs recherches appel au puissant concours que l’emploi des mathématiques peut fournir à la logique ordinaire ou qui, du moins, ont contribué à vulgariser par leurs ouvrages théoriques, critiques ou historiques une science dont ils sont devenus les adeptes.

En outre des auteurs que nous avons rencontrés précédemment, nous nous bornerons donc à signaler dans la période contemporaine :

En Allemagne.

Julius Lehr (Grundbegriffe und Grundlagen der Volkswirthschaft, Leipzig, 1893, et de nombreux articles notamment dans le Jahr Nalionalök. u. Statist. et le Vierteljahrschr. Volkswirth.). — J. Schumpeter (Das Wesen und das Hauphinhalt der theoretischen Nationalökonomie, Leipzig, 1908).

En Angleterre.

Philip H. Wicksteed (The alphabet of economic science I^re part. Elements of the theory of value and worth, Londres, 1888 et plusieurs articles du Dictionary of political economy de Palgrave, Londres, 1894-1896).

En Danemark.

Harald Westergaard (Mathematiken i Nationalökonomiens Tjeneste dans le volume Smaaskrifter Tilegne de A.-F. Krieger, Copenhague, 1887 ; Indledning til Studiet of Nationalökonomien, Copenhague, 1891).

En Hollande.

D’Aulnis de Bourouill (Het Inkomen der Maatschappij. Eene Prœve van theoretische Slaathuishoudkunde, Leyde 1874). — A. Beaujon (Wiskunde in de Economie, dans l’Economist, Amsterdam, oct. 1889. À propos de la théorie des prix, dans la Revue d économie politique, Paris, fév. 1890). — A.-J. Cohen Stuart (Bijdraje tot de Theorie der progressieve Inkomstenbelasting, La Haye. 1889). — Mees (Junior).

En Italie.

E. Barone, dont les travaux, notamment les Principi di economia politica (Rome, 1889), ont largement contribué à la vulgarisation des théories de l’économie pure, en mettant « à la disposition de ceux qu’avaient rebutés les exposés souvent très ardus de ces auteurs [Walras et Pareto] l’instrument le plus commode et le plus maniable pour connaître et comprendre leurs théories » (Charles Rist). Il convient de citer également les nombreux articles théoriques que M. Barone a publiés dans le Giornale degli Economisti depuis 1894 — J.-B. Antonelli (Sulla teoria matematica della economia politica, Pise, 1886). — G. Rossi (La matematica applicata alla teoria della richezza sociale, dans Studi bibliog. storici e critici e nuovi ricerce, Reggio Emilia, 1889) — P. Bonin-Segni (Articles dans le Giornale degli economisti) — Luigi Amoroso — V. Furlan — Tullio Martello — Guido Sensini et même M. Pantaleoni quoiqu’il appartienne plutôt à l’École Autrichienne. Ses Principii di economia pura (Florence 1890, 2^e éd., 1894), qui contiennent un résumé des travaux sur l’utilité, rendirent « pour la première fois accessibles à tous les démonstrations profondément originales et vigoureuses, quoique parfois abstraites, de Gossen » (A. Marshall).

En Suède.

Knut Wicksell (Uber Wert, Kapital und Rente nach den neueren nationalökonomischen Theorien), Iéna, 1893.

Il existe d’ailleurs diverses bibliographies très riches, quoique incomplètes, des œuvres des économistes qui ont eu recours à l’emploi des mathématiques.

La plus ancienne date de 1878, elle a toute une histoire. Elle fut dressée par Jevons et Walras eux-mêmes à la suite de la constatation de la coïncidence des résultats auxquels ils étaient parvenus chacun de son côté. « Il est assez naturel », dit Walras^[157], « que M. Jevons et moi, mis en éveil par cette coïncidence singulière, nous ayons pris soin de nous enquérir des diverses tentatives qui avaient précédé les nôtres, et que nous ayons été ainsi amenés à dresser de compte à demi la Bibliographie des ouvrages relatifs à l’application des mathématiques à l’économie politique. » « Dans ce but, » dit Jevons^[158], « je dressai la liste chronologique de tous les ouvrages mathématico-économiques que je connaissais, alors au nombre d’environ 70 : cette liste fut, grâce à l’obligeance de l’éditeur, M. Giffen, imprimée dans le numéro de juin 1878 du Journal of the London Statistical Society, et adressée aux principaux économistes, aux fins d’additions et de corrections. Mon ami, M. L. Walras, recteur de l’Académie de Lausanne, après y avoir fait lui-même des additions considérables, la communiqua au Journal des Économistes décembre 1878) ». Cette bibliographie, améliorée grâce aux indications de différentes personnes citées par l’auteur, fut insérée par Jevons dans la deuxième édition de sa Theory, puis, après son décès, elle fut complétée par les soins de M^me  Jevons telle qu’elle figure dans la troisième édition (1888).

Depuis cette époque, le professeur Irving Fisher a dressé successivement deux bibliographies.

La première constitue l’appendice IV de ses Mathematical investigations (1892)^[159] ; elle comprend une liste de publications choisies parmi celles qui sont citées par W. St. Jevons (Selected from Jevons) et une liste additionnelle (Extension of Jevons’ bibliography).

La seconde se trouve à la suite de la traduction en langue anglaise des Recherches de A.-A. Cournot (1897)^[160] ; elle est divisée en quatre périodes :

de Ceva à Cournot 1711-1837.

de Cournot à Jevons, 1838-1870.

de Jevons à Marshall, 1871-1889.

de Marshall à nos jours, 1890-1897.
et dans chaque période les différentes publications sont classées systématiquement.

L’examen de cette liste, qui comprend 327 publications réparties sur 187 années, est des plus encourageant pour les partisans de l’emploi des mathématiques en économie politique, car elle peut être résumée dans le tableau suivant :

	1re Période	2e Période	3e Période	4e Période
Durée en années	127	33	19	8
Nombre des publications	27	44	114	142

qui permet de bien augurer de l’avenir.

Un extrait de cette dernière bibliographie figure dans l’Introduzione alla economia matematica de F. Virgilii et C. Garibaldi^[161].

1. Le livre de G. Ceva a été analysé par F. Nicolini dans le numéro d’octobre 1878, du Giornale degli economisti, sous ce titre : Un antico economista matematico.
2. Ce n’est guère qu’accidentellement que les autres auteurs de cette époque dont les noms sont cités, soit dans la bibliographie de W. St. Jevons (Cf. II, IV), soit dans l’Histoire des doctrines… [p. 5] de L. Cossa (part. I, ch. vi, § 4), ont fait appel aux mathématiques pour traiter des questions économiques.
3. Vol. I., Brescia, 1765. Cet article est reproduit dans les Scrittori classici italiani di economia politica du baron Custodi, Partie moderne, vol. XII, Milan, 1804.
4. Théorie… [p. 91], préf. de la 2^e éd., p. 39
5. À Londres et mis en vente « à Lausanne en Snisse, chez François Grasset et C^ie »
6. Sur Isnard, voir L. Renevier : Les théories économiques de Achille-Nicolas Isnard d’après son ouvrage « Traité des richesse », Poitiers, 1909.
7. Traité des richesses, t. I, 1. I, ch. i, sect. 1^re.
8. Ce travail figure dans le t. V de la Nuova raccolta d’opusculi di autori siciliani, Palerme, 1792.
9. D’après l’Introduzione… [p. 259] de F. Virgilii et C. Gari-baldi.
10. Nous avons limité cette seconde période à l’année 1870 — c’est-à-dire à l’apparition des œuvres de W. St. Jevons et de L. Walras — bien que H. -H. Gossen, que nous classerons parmi les fondateurs de l’économie pure, ait publié son livre en 1854, parce que, ainsi que nous le verrons, cet ouvrage n’a acquis, en fait, droit de cité qu’après la publication des œuvres de W. St. Jevons et de L. Walras.
11. J. Bertrand, Journal des savants, numéro de septembre 1883 et aussi Bulletin des sciences mathématiques de la même année.
12. Recherches… [p. 76], préf. p. vii.
13. Histoire de l’économie politique, 4^e éd., Paris, 1860, t. II, p. 323
14. Loc. cit.
15. Cf. A. Montanari, La matematica applicata all’ economia politica da Cesare Beccaria, Guglielmo Silio, L. M. Valeriant ed Antonto Scialoja, Reggio-Emilia, 1899.
16. Cf. A. Graziani, Le idee economiche degli scrittori emiliani et romagnoli sino al 1848, Modena, 1893, ch. viii, § 2.
17. Melchiorre Gioja, un défenseur de la théorie du coût de production.
18. Si nous avons énoncé ces titres tout au long, bien que cela puisse paraître oiseux, c’est parce que ces deux publications ne sont pas mentionnées dans la bibliographie dressée par W. St. Jevons (Cf. II, IV) qui est la plus répandue.
19. Histoire des doctrines… [p. 5], part. I, ch. vi, § 4.
20. Cet ouvrage, qui a eu une 2^e édition (Rostock, 1842), a été traduit en français par J. Laverrière (Paris, 1851).
21. Le premier a été traduit en français par M. Wolkoff (Paris, 1857).
22. Isolirte Staat, 2^e part., vol. I, § 18.
23. Vol. III (1829), pp. 191-230 ; IV (1831), pp. 155-198 ; IX (1850), pp. 128-149 et 2^e part., pp. 1-7 (Ces deux derniers mémoires ont été traduits en italien dans la Biblioteca dell’economista, 3^e sér., vol. II, pp. 1-65).
24. Théorie... [p. 91], préf. 2^e éd., p. 21.
25. W. St. Jevons, Théorie... [p. 91], préf. 2^e éd., p. 28.
26. Recherches, préf. p. xi.
27. Encyclopédie… [p. 149], § 14 n. 22, p. 606 et Manuel… [p. 143], §§ 73 et s., p. 600. Voir infra, III, V, 4.
28. Mathematical psychics [p. 119], App. V, p. 116.
29. Cf. V. Pareto, Di un errore del Cournot nel trattare l’economia politica colla matematica dans le Giornale degli economisti, numéro de janvier 1892.
30. Il est intéressant de noter à ce propos que dès le xviii^e siècle G. Ortes, dans son Calcolo sopra il valore delle opinioni umane, avait illustré l’exposé de ses idées avec des courbes qu’il s’était, il est vrai, borné à décrire minutieusement, sans les tracer. (Dictionary of political economy de R.-H. Inglis Palgrave^e siècle, vol. III, Londres, 1899, p. 44.)
31. Voir cependant l’article de M. A. Aupetit dans le numéro de mai 1905, entièrement consacré à Cournot, de la Revue de métaphysique et de morale.
32. Cette traduction faite par M. N.-T, Bacon et publiée à New-York en 1897, dans la collection des Economie Classics éditée par W.-J. Ashley, est en quelque sorte aujourd’hui la meilleure édition des Recherches. Le traducteur a, en effet, pris soin de rectifier les erreurs qui s’étaient glissées dans l’œuvre originale, à l’exception pourtant de deux d’entre elles, dont la rectification aurait sérieusement affecté les raisonnements et qui portent respectivement sur les formules (6) de la page 122 [140 de l’original], dans lesquelles $\epsilon$ devrait être remplacé par zéro, et sur deux inégalités de la page 158 [183 de l’original] dont le sens devrait être renversé (Cf. pp. vi et vii de la préface, due à M. Irving Fisher de la traduction en question). — Il existe également une traduction en italien des Recherches (Biblioteca dell’ economista, 3^e série, vol. II, Turin, 1878), mais elle n’offre pas les avantages de la traduction anglaise.
33. Cf. L. Walras, Éléments… [p. 106], 41^e leç., §§ 385 et s.
34. Par une de ces coïncidences dont on rencontre maints exemples dans l’histoire de l’économie politique mathématique, l’étude des variations de la demande en fonction du prix avait été déjà envisagée en Allemagne par K.-H. Hagen (Von der Staatslehre und von der Vorbereitung zum Dienste in der Staatsverwaltung, Kœnigsberg, 1839), presque en même temps qu’en France par A. -A. Cournot.
35. Stuttgart, 1871 (et non 1873, comme il est parfois indiqué).
36. Cf. l’art. de M. F.-Y. Edgeworth dans le Dictionary of political economy de R.-H. Palgrave, vol. II, Londres, 1896, p. 473.
37. Les diverses études de F. Jenkin ont été réunies, sous le titre Papers literary, scientific, etc., en deux volumes publiés à Londres en 1887-88.
38. Cet auteur se qualifiait de Ancien répartiteur royal du gouvernement de Prusse.
39. W. Whewell (op. cit.) et J. Tozer (Mathematical investigation… Cambridge philosophical transactions, vol. VI, 1838, pp. 507-522) avaient déjà usé de simplifications de ce genre.
40. Nous adoptons l’expression d’utilité finale (final utility), imaginée par Jevons, pour désigner l’utilité de l’élément le moins utile d’une certaine quantité d’un bien donné, parce que c’est celle qui est consacrée par l’usage en France. Mais nous nous réservons cependant de faire appel, à l’occasion des œuvres d’auteurs déterminés, aux autres désignations qui ont pu paraître préférables à ceux-ci, telles que les expressions de utilité marginale (marginal utility) et de utilité limite (Grenznutzen) ou mieux liminale, qui sont d’ailleurs plus satisfaisantes que la première, ou que le mot de rareté, qui présente par contre l’inconvénient de prêter à des confusions en donnant à penser qu’il n’est question que de la limitation en quantité, alors qu’il s’agit également de l’utilité (Voir un exemple typique de ces confusions dans les Comptes rendus des séances et travaux de l’Académie des sciences morales et politiques, numéro de janvier 1874, p. 119).
41. Brunswick, 1854 ; Berlin, 1889 (réimpression).
42. Geschichte der Nationalökonomie in Deutschland, Munich, 1874.
43. Vienne, 1858.
44. Numéro d’avril 1885. (Cette étude figure également dans la III^e section des Études d’économie sociale, de L. Walras.) — Antérieurement G.-D. Hooper avait également fait paraître un article sur H. -H. Gossen dans le Journal of the London statistical society, numéro de septembre 1879, pp. 727-733.
45. Éléments… [p. 106], 16^e leç., § 164.
46. Entwickelung, p. 85.
47. Sur la manière dont Gossen a envisagé cette question, qui tient une place importante dans son œuvre, voir l’Histoire des doctrines… [p. 21] de Ch. Gide et Ch. Rist, LV, ch. ii, § 3 notamment pp. 654, 655, 657 et notes.
48. Loc. cit.
49. Revue anglaise Nature, numéro du 5 septembre 1889, p. 435.
50. Ce livre, publié pour la première fois à Londres en 1871, a eu, en 1879, 1888 et 1911 trois autres éditions (dont les deux dernières ne sont, du reste, que des réimpressions de la seconde) et il a été traduit en français, sous le titre Théorie de l’économie politique, par MM. H.-E. Barrault et Maurice Alfassa, au travail de qui nous nous référerons.
51. Voir sur ce point A. Marshall, Principes… [p. 100], LV, ch. xiv, §§6 et 7.
52. Théorie, préface de la 2^e édition, p. 32.
53. Le compte rendu de cette communication a été publié par le Journal of the statistical society of London en juin 1866 (vol. XXIX) et sa traduction, par MM. Barrault et Alfassa, figure à la suite de celle de la Theory of political economy.
54. Théorie, ch. iii p. 103.
55. Théorie, ch. iv, p. 163.
56. Éléments… [p. 106], 11^e leç., §§ 111 et s.
57. Nous avons parlé dans ce qui précède d’unité de prix parce que c’est là, croyons-nous, la forme sous laquelle la condition d’équilibre entre les divers groupes de trafiquants se présente sous la forme la plus simple ; mais il n’est nullement indispensable, comme pourrait le faire supposer une critique adressée par Walras à Jevons (Éléments… [p. 106], 16^e leç., § 163), de faire intervenir la notion de prix, qui peut être entièrement exclue de l’économie pure, ainsi que l’a montré M. V. Pareto (Manuel… [p. 143], ch. iii).
58. Il y a dans la Théorie une manifestation absolument typique de cet état d’esprit : c’est la formule lapidaire suivante, critiquée, à juste titre, par MM. A. Marshall (loc. cit.) et Irving Fisher (Mathematical Investigations… [p. 136], part. I, ch. v, § 1), dans laquelle Jevons n’a pas craint d’établir un enchaînement entre une série de faits qui se suivent chronologiquement il est vrai, mais ne présentent pas de rapports de causalité :

    « Cost of production détermines supply,

    « Supply détermines final degree of utility

    « Final degree of utility détermines value »,

    (Theory, ch. iv, in fine.)

59. Théorie, ch. v, p. 269.
60. Ibid., ch. i, p. 54.
61. Ibid., ch. v, p. 269.
62. Ibid., ch. vii, p. 309.
63. Ibid., préface de la 2^e éd., p. 41.
64. L’accident qui mit, comme l’on sait, fin à ses jours prématurément l’empêcha de réaliser ce projet.
65. Théorie, préf. de la 2^e éd., p. 9.
66. Cpr. l’article de M. Jean Lescure, Revue d’Économie politique, numéro de juin 1910.
67. Londres (5 éd. : 1890, 1891, 1895, 1898, 1907). Trad. franç. par MM. F. Sauvaire-Jourdan et F. Savinien Bouissy, sous le titre Principes d’économie politique, Paris (1907-1909).
68. A. Marshall, Distribution and exchange dans l’Economie Journal, numéro de mars 1898, cité dans l’Histoire des doctrines… [p. 21] de Ch. Gide et Ch. Rist, l. V, ch. i, in fine.
69. Citation de M. Ch. Gide dans son Cours d’économie politique, 2^e éd. (Paris, 1911), Not. Gén., ch. iii, sect. iv, § 2 note in fine.
70. Principes, l. V, ch. vi.
71. Ibid., l. III, ch. vi, sect. iv, § 2.
72. La rente ou bénéfice des consommateurs (consumers’ surplus) est, comme l’on sait, le bénéfice subjectif représenté par la différences entre la dépense correspondant à l’acquisition d’une certaine quantité de marchandise au cours du marché et celle que les consommateurs seraient disposés à faire plutôt que de se priver de cette quantité de marchandise. Or, l’emploi de courbes de demande et d’offre, en fonction des prix, permet de rendre en quelque sorte tangible ce bénéfice, car il est clair que si DD’ et OO’ (fig. 1) représentent respectivement une courbe de demande et une courbe d’offre, dont le point d’intersection A détermine par son abscisse le prix courant, la rente des consommateurs (abstraction faite des variations de l’utilité finale de la monnaie), est représentée par l’aire du triangle AFD, de même que, sous certaines conditions (Cf. Principes, l. V, ch. xi, in fine), la rente des producteurs est représentée par l’aire du triangle AFO.

    
    

    

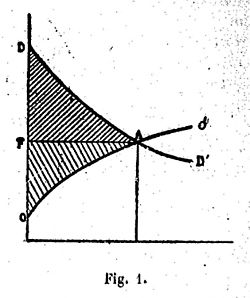
73. Nous dirons quelques mots de ce phénomène à propos des théories de L. Walras, qui l’a envisagé à peu près au même point de vue que A. Marshall. (Cf. III, I, 2.)
74. Il était réservé à M. V. Pareto de faire, pour la première fois l’analyse approfondie de cette question (Cf. III, V, 5).
75. Lausanne et Paris, 1900 (Les premières éditions portent les dates suivantes : 1874-1877, 1889, 1896).
76. L’inscription, accompagnant un médaillon qui, à l’Université de Lausanne, — non loin de celui de Sainte-Beuve, son parent — rappelle aux étudiants les traits du maître, est rédigée en ces termes a « À Léon Walras, né à Évreux en 1834, professeur à l’Académie et à l’Université de Lausanne, qui, le premier, a établi les conditions générales de l’équilibre économique, fondant ainsi l’« École de Lausanne ». Pour honorer cinquante ans de travail désintéresser ».
77. Éléments, 10^e leç., § 100.
78. Dans une lettre dont nous reproduirons plus loin la partie essentielle.
79. Paris, 1831. — Walras étant dans un très grand nombre d’ouvrages qualifié d’ « économiste suisse » du fait qu’il a consacré une grande partie de sa vie à l’Université de Lausanne, nous ne croyons pas inutile de rappeler ici le curriculum vitæ de son père, tel qu’il figure dans le Dictionnaire de l’économie politique, de Ch. Coquelin et Guillaumin (4^e tirage, 1873) :

    « Walras (Antoine, Auguste) inspecteur de l’Académie du Nord, né à Montpellier en 1801. En 1820 il entra à l’École Normale ; en 1831 il devint professeur de rhétorique au collège d’Évreux, et publia, peu après son arrivée dans cette ville, son premier ouvrage d’économie politique, sous les auspices de la Société libre de l’Eure. L’année suivante il ouvrit un cours d’économie politique ; et, après avoir été, de 1833 à 1835, principal du collège d’Évreux, il vint à Paris, professa l’économie politique à l’Athénée de cette ville, et, après avoir été reçu agrégé en 1840, il fut tour à tour professeur de philosophie au lycée de Caen et professeur de littérature française à la faculté des lettres de cette même ville. »

80. D’abord dans sa réponse — dont nous citerons un passage ultérieurement (III, I, 2) — à la lettre précitée de Jevons, puis dans la préface de la 1^re édition des Éléments.
81. Nous avons pensé, en effet, qu’un simple aperçu de la théorie mathématique de la monnaie n’ajouterait rien à ce que nous disons par ailleurs, la monnaie étant, en somme, une marchandise au même titre que les autres biens économiques ; et d’un autre côté un exposé détaillé de cette question aurait dépassé les limites de l’espace que nous aurions pu lui consacrer dans un travail aussi général que celui que nous avons entrepris. Cet exposé fait, du reste, l’objet d’un ouvrage remarquable dû à M. A. Aupetit, Essai sur la théorie générale de la monnaie, Paris, 1901.
82. La 4^e édition des Éléments comprend en outre, en supplément, une Théorie géométrique de la détermination des prix, qui n’est que la traduction, sous une forme géométrique, des théories de l’échange et de la production, et des Observations sur le principe de la théorie des prix de MM. Auspitz et Lieben, dont nous aurons l’occasion de parler (infra, III, 3) à propos de ces auteurs.
83. Kommerzielle Trassirung der Verkehrswege (Hanovre, 1872, 2^e éd., 1887).
84. Der zweekmässigte Standort einer gewerblichen Anlage, dans la Zeitschrift des Vereins deutscher Ingenieure (1882).
85. Wirthschaftliche Fragen des Eisenbahnwesens, dans la Centralbatt der Bawerwaltung (1883).
86. Cf. p. 163
87. Leipzig, 1885.
88. Il revient, en effet, au même d’attribuer une loi linéaire aux variations du degré d’utilité ou une loi parabolique aux variations de l’utilité totale.
89. Leipzig, 1885.
90. Londres, 1881.
91. Mathematical Psychics, App, V.
92. The mathematical theory of political economy, dans la revue anglaise Nature, numéro du 5 septembre 1889.
93. On the application of mathematics to the political economy. Cette communication a été publiée dans la revue anglaise Nature, numéro du 19 septembre 1889, ainsi que dans le Journal of the Royal statistical Society, numéro de décembre 1889 (auquel nous nous référerons sous la désignation : Discours) et dans le Report of the British Association for the Advancement of Science de la même année.
94. Notons de plus que M. Edgeworth a rédigé dans le Dictionary of political economy de R.-H. Inglis Palgrave (Londres, 1894-1896), un certain nombre d’articles relatifs à l’économie mathématique et aux économistes mathématiciens.
95. Cf. Sidgwick, Political Economy, B. II, ch. i.
96. Théorie… [p. 91], ch. iii, p. 119.
97. « Es kann ein Erzieher einem Knaben, um ihn gegen Weheleidigkeit abzuhärten, für die tapfere, freiwillige Erduldung von Schmerzen ein sehnlich begehrtes Spielzung ; in Aussicht stellen. So untergeordnet das Vorkommen solcher Falle auch sein mag, so wichtig ist es für die Theorie festzustellen, dass Arbeit und Arbeits-plage doch nicht der einzige Umstand ist, auf den sich… die Wertschätzung gründen kann. » (Konrad’s Jahrhuch, 1866, p. 43).
98. La théorie mathématique de l’offre et de la demande, dans la Revue d’Économie politique, numéro de janvier 1891, pp. 26-27.
99. Cpr. : « Commercial competition might be likened to a system of lakes flowing into each other ; industrial competition to a system of vessels so communicating by means of valves, that when the level in one exceeded that of another to a certain extent, then per saltum a considerable portion of the contents of that one (a finite différence as compared with the differentials of the open system) is discharged into the other. » (Discours, p. 545 note).
100. Voir Todhunter, Researches in the calculus of variations (ch. i et passim).
101. Revue d’Économie politique, numéro de janvier 1891, p. 24.
102. Revue d’Économie politique, numéro de janvier-février 1890.
103. « Les « sacrifices et les efforts », mais ce n’est qu’un autre terme pour ce que Walras appelle les services des capitaux personnels. » Loc, cit., p. 84.
104. Revue d’Économie politique, numéro de janvier 1891, p. 25.
105. Giornale degli Economisti, numéro d’octobre 1897.
106. Idem, numéro de juillet 1897.
107. Discours, pp. 547-549 et note l.
108. Mathematical Psychics, pp. 37-52.
109. Cpr. A. et M.-P. Marshall, Economics of Industry, Londres 1879, p. 215.
110. « Axiom. — Pleasure is measurable, and all pleasures are commensurable ; so much of one sort of pleasure felt by one sentient being equateable to so much of other sorts of pleasure felt by other sentient. » (Mathematical psychics, p. 59).
111. « Just perceivable increments [of pleasure] are equateable » (Mathematical psychics, p. 99).
112. Mathematicals psychics, p. 57.
113. Mathematical Investigations… [p. 136], Préf. pp. 4 et 5.
114. J.-K. Ingram, Histoire… [p. 36], ch. vi, p. 335.
115. Mathematical psychics, p. 99.
116. Discours, p. 554.
117. Leipzig, 1889.

118. 

     
     Cela résulte immédiatement de ce fait que l’égalité numérique de l’utilité et du prix relatifs à une quantité de produit donnée $oq$ implique le parallélisme de la tangente à la courbe d’utilité $pt$ et du rayon vecteur $op'$ de la courbe de demande aux points correspondant à la quantité considérée (fig. 2).

119. Les courbes dérivées se prêtent, en effet, tout particulièrement à la mise en évidence de la rente des consommateurs ou, plus généralement, du profit du commerce (gain of trade), suivant l’expression du professeur Edgeworth (Discours [p. 120], note c), ce profit, pour une quantité de produit $oq$ (fig. 2) donnée, étant représenté par la différence $p'p$ des cotes des points correspondants de la courbe primitive et de la courbe dérivée.
120. Nous avons vu (II, II, 4) que Walras est parvenu ultérieurement à élaborer une théorie purement géométrique indépendamment de toute supposition de ce genre.
121. Traité… [p. 33], t. I, ch. iv.
122. Numéro de mai-juin 1890 (Cet article figure également à la fin de la 4^e édition des Éléments... [p. 106]).
123. Numéro de novembre-décembre 1890.
124. La teoria dei prezzi dei Signori Auspitz e Lieben e le osservazioni del Professore Walras dans le numéro de mars 1892, du Giornale degli economisti.
125. Extrait des Transactions of the Connecticut Academy, vol. IX, juillet 1892.
126. Mathematical investigations, part. I, ch. i, § 5 note.
127. Op. cit., part. I, ch. i.
128. Op. cit., préf., p. 4.
129. Ibid., part. I, ch. ii, § 1.
130. Dont le professeur Edgeworth semble avoir eu également l’idée à la même époque. Cf. Revue d’Économie politique, numéro de janvier 1891, p. 27.
131. Cf. Revue d’Économie politique, numéro de mars 1908.
132. E. Barone, Giornale degli Economisti, numéro de mai 1894.
133. Voir Mathematical Investigations, préf., p. 4.
134. Numéro de mars 1893.
135. Mathematical Investigations, part. II, chap. i, § 5.
136. Principes... [p. 100], t. II, App. A, n. XII bis, p. 589.
137. New-York, 1912, réimp., 1913.
138. New-York, 1897, 3^e édit, 1906.
139. Voir en particulier : Economie Journal, 1894, vol. IV, pp. 527-237 ; Publ. Amer. Econ. Assoc., 1896, vol, XI, n^o  4 ; American Economie Review, mars 1913 ; Quarterly Journal of Economics, février 1913 ; Annales of the American Academy of Political and Social science, juillet 1913, pp. 133-139.
140. I, Lausanne, 1896 ; II, Id., 1897.
141. Milan, 1906.
142. Paris, 1909.
143. M. Pareto a publié à partir de 1892 un très grand nombre d’articles dans le Giornale degli Economisti, dont la substance a été en grande partie incorporée à ses ouvrages.
144. Éléments… [p. 106], p. xi.
145. Cours, t, I, préf. p. iv.
146. Walras n’avait eu recours qu’à l’algèbre et à la géométrie analytique plane.
147. C’est ainsi que dans un dîner, par exemple, il ne serait pas aussi agréable de commencer par le dessert et de terminer par le potage que de procéder dans l’ordre normal inverse.
148. Essai sur le principe de population, l. III, ch. v.
149. Cours, II, n^o  978, p. 338.
150. Cours, I, préf., p. iii.
151. Par opposition à irraisonnées, ce qui ne veut pas dire nécessairement illogiques (Voir sur ce sujet un article de M. Pareto dans la Rivista italiana di sociologia, XIV, fasc iii-iv, mai-août 1910).
152. Manuel, ch. iii, § 1.
153. T. I, vol. 4, fasc. 4, Paris, 1911.
154. Les phénomènes du type II, sont ceux qui correspondent à l’exercice d’un monopole parce que la possibilité de modifier à leur profit les conditions d’un marché est évidemment réservée à ceux qui jouissent, par rapport aux autres individus, d’un avantage spécial, c’est-à-dire, d’un monopole.
155. Manuel, ch. iii, § 49.
156. Encyclopédie, § 48.
157. Journal des Économistes, numéro d’avril 1885, p. 71.
158. Théorie… [p. 91], préf. de la 2^e éd., p. 15.
159. Cf. p. 136.
160. Cf. p. 79.
161. Cf. p. 259.