Le Traité des Corps flottants d’Archimède/Livre I

Archimède

Des corps flottants

Traduction par Adrien Legrand.
Gauthier-Villars et fils, 1891 (p. 11-24).

PREMIER LIVRE.

PREMIÈRE HYPOTHÈSE.

Supposons que tout liquide soit de telle nature que, si l’on considère les parties de même niveau^[1] et continues, la moins poussée cède à celle qui l’est plus. Disons encore que chacune des parties est poussée par le liquide qui est au-dessus d’elle suivant la verticale [et cela^[2], lorsque le liquide descend dans quelque chose et supporte quelque autre chose].

Proposition I.

Une surface étant coupée par un plan, qui passe par un point déterminé^[3], si la section est une circonférence ayant ce point pour centre, la surface sera sphérique.

Fig. 1.

Soit une surface coupée par un plan passant en κ de façon que l’intersection soit toujours une circonférence ayant pour centre κ. Supposons que ce ne soit pas une surface de sphère. Toutes les lignes allant du centre de la circonférence à la surface ne seront point égales entre elles.

Soient donc les points αβγδ sur la surface, et supposons ακ, κβ inégales entre elles. Par κα, κβ faisons passer un plan dont la section avec la surface soit la ligne αβγδ. Cette ligne sera une circonférence ayant pour centre κ, puisque telle a été notre position sur la nature de la surface en question.

Donc les lignes κα, κβ ne sont point inégales, et, nécessairement, la surface en question est sphérique.

Proposition II.

Si un liquide est en état d’équilibre et d’immobilité, la forme de sa surface est celle d’une sphère ayant pour centre le centre de la Terre.

En effet, supposons le liquide en état d’équilibre et d’immobilité. Coupons sa surface avec un plan passant par le centre de la Terre. Soit κ le centre de la Terre. Soit αβγδ l’intersection de la surface du liquide avec ce plan.

Fig. 2.

Je dis donc que la ligne αβγδ est une circonférence, dont le centre est κ. En effet, s’il n’en est pas ainsi, les droites menées de κ à la ligne αβγδ ne seront pas égales. Prenons donc une droite qui, comparée à celles qui vont vers αβγδ, soit plus grande que les unes, plus petite que les autres. Avec cette ligne pour rayon, en prenant κ comme centre, décrivons une circonférence. Cette circonférence passera en partie au delà, en partie en deçà de αβγδ, puisque son rayon est plus grand que certaines des droites menées jusqu’à αβγδ, plus petit que certaines antres. Soit ζβε la circonférence ainsi décrite. Menons la droite κβ et les droites κζ et κελ formant des angles égaux^[4]. Décrivons encore en prenant κ pour centre, une circonférence ξοπ dans le même plan et dans le liquide.

Les parties de liquide, situées sur la circonférence ξοπ, sont de même niveau et continues entre elles^[5]. Celles qui sont situées en ξο sont poussées par le liquide ξοβζ sous βζ ; celles en οπ par le liquide ποβε sous βε. Ainsi les parties du liquide, situées sur l’arc de cercle ξο, ne sont pas poussées comme celles situées en οπ. Par conséquent, les moins poussées céderont aux plus poussées ; nous n’avons donc pas affaire à un liquide en équilibre.

Or, nous l’avions supposé en état d’équilibre et d’immobilité. Il faut donc nécessairement que la ligne αβγδ soit une circonférence ayant pour centre κ.

On démontrera de même que, de quelque façon que l’on coupe la surface du liquide par un plan passant au centre de la Terre, l’intersection sera une circonférence ayant pour centre celui de la Terre. Il est donc évident que la surface d’un liquide en équilibre a la forme d’une sphère ayant le même centre que la Terre, puisque cette surface est telle que, coupée d’un plan par un point fixe, elle donne pour section une circonférence ayant pour centre le point par lequel est mené le plan dont on la coupe.

Proposition III.

Un solide de même volume et de même poids^[6] que le liquide, dans lequel il est abandonné, y enfoncera de façon à n’émerger nullement au-dessus de la surface, mais^[7] à ne pas descendre encore plus bas.

En effet, supposons qu’un solide de même poids que le liquide y soit abandonné, et, si toutefois cela se peut, qu’il émerge au-dessus de la surface. Supposons le liquide en équilibre et immobile. Fig. 3.
Imaginons un plan qui passe par le centre commun de la Terre et du liquide et par le solide. Soit αβγ son intersection avec la surface du liquide, εζηθ le corps flottant^[8], κ le centre de la Terre. Soit βγηθ la partie du solide immergée, βεζγ celle qui émerge.

Représentons-nous le solide comme compris dans une pyramide, dont la base est un parallélogramme à la surface du liquide et dont le sommet est le centre de la Terre. Disons que l’intersection αβγ est une circonférence et que celles des faces de la pyramide avec le plan sont κλ, κμ. Décrivons dans le liquide, autour de κ pris pour centre, une autre surface de sphère sous εζηθ, ce sera ξοπ ; et supposons-la coupée (suivant cette ligne ξοπ) par la surface du plan. Supposons une autre pyramide semblable, égale et contiguë à celle qui contient le solide. Soient κμ, κν les sections de ses faces par le plan. Envisageons, dans le liquide, un volume de ce liquide même, soit ρστυ, égal et identique à la partie βηγθ du solide qui se trouve immergée.

Les parties de liquide qui sont dans la première pyramide sous la surface coupée en ξο et celles de la seconde sous οπ sont de même niveau et continues. Or^[9] elles ne sont pas également poussées. En effet, celles qui sont en ξο sont poussées : 1^o  par le solide εζηθ, 2^o  par le liquide situé entre les surfaces λμ, ξο et les faces de la pyramide ; celles en οπ le sont : 1^o  par le solide ρστυ et 2^o  par le liquide situé entre les surfaces μν, οπ et les faces de la pyramide. Mais le poids du liquide μνοπ sera moindre que celui du liquide λμξο. En effet, la partie liquide ρστυ est moindre que le solide εζηθ, puisqu’elle est égale à la partie βγηθ et qu’on a supposé le solide de même poids et de même dimension que le liquide. Le reste des parties liquides est égal de part et d’autre.

Il est donc évident que le liquide, situé en οπ, cédera à celui qui est situé en οξ et qu’il ne sera pas en équilibre. Or on l’a supposé immobile^[10].

Donc, aucune partie du solide en question n’émergera. Et le solide immergé ne descendra pas au fond, car toutes les parties du liquide, situées au même niveau, seront également poussées, puisque le solide est de même poids que le liquide^[11].

Proposition IV.

Tout corps solide plus léger que le liquide où il est abandonné ne sera pas complètement immergé, mais restera en partie au-dessus de la surface liquide.

En effet, supposons un corps plus léger que le liquide et qui y est abandonné. Supposons, si toutefois la chose est possible, qu’il y soit totalement immergé sans qu’aucune partie s’élève au-dessus de la surface, que d’ailleurs^[12] le liquide reste immobile.

Fig. 4.

Imaginons maintenant un plan mené par le centre de la Terre, le liquide et le solide. Soit αβγ la circonférence suivant laquelle ce plan coupe la surface du liquide ; la section du solide est représentée par la figure en ζ, le centre de la Terre par κ. Imaginons, comme précédemment, une pyramide comprenant ζ et ayant pour sommet le point κ ; ses faces seront coupées par le plan αβγ suivant ακ, κβ. Admettons une autre pyramide égale et semblable, dont les faces sont coupées par le plan αβγ suivant κβ, κγ. Décrivons ensuite dans le liquide une autre surface de sphère située sous le solide et ayant κ pour centre ; elle sera coupée par le même plan suivant ξοπ.

Que l’on se représente, dans la seconde pyramide, un volume de liquide η^[13] égal au solide ζ. Les parties liquides de la première pyramide, situées sous les deux surfaces en ξο et celles de la seconde, situées également sous les deux surfaces en οπ, sont de même niveau et continues entre elles. Mais elles ne peuvent être également poussées. Car celles de la première pyramide le sont par le solide en ζ et par le liquide qui l’entoure et qui occupe la partie de pyramide αβοξ. Celles de la seconde sont poussées par le liquide en η et le liquide qui l’entoure et qui occupe la partie de pyramide ποβγ. Mais le poids de ce qui est en ζ est moindre que celui de ce qui est en η, puisque nous supposons le solide égal en volume au liquide, mais plus léger^[14]. Quant au liquide qui entoure ζ et η, son poids est égal dans les deux parties de pyramides qui sont égales entre elles^[15]. Donc, la portion de liquide située sous les deux surfaces^[16] suivant l’arc de cercle οπ est la plus poussée des deux. Elle chassera donc la moins poussée et le liquide ne peut dès lors rester immobile. Donc, le solide ne sera pas entièrement immergé ; une portion en restera au-dessus de la surface du liquide^[17].

Proposition V.

Un solide plus léger que le liquide dans lequel on l’abandonne y enfonce de telle façon qu’un volume de liquide égal à la partie immergée ait le même poids que le solide entier. (Voir fig. 3.)

Faisons les mêmes constructions que ci-dessus, et supposons le liquide immobile. Soit un solide εζηθ plus léger que le liquide. Pour que le liquide soit immobile, il faut que les parties de même niveau soient également poussées. Par conséquent, le liquide sera également poussé sous les surfaces déterminées par les arcs de cercle ξο et οπ. Les poids qui les pressent seront donc égaux.

Mais le poids du liquide dans la première pyramide, diminution faite du solide βηθγ, est égal au poids du liquide de la seconde moins la partie πστυ. Donc, il est évident que le poids εζηθ est égal à celui du liquide πστυ. Donc, un volume de liquide égal à la partie immergée pèse autant que le solide entier.

Proposition VI.

Lorsqu’un corps est plus léger que le liquide où on l’enfonce et remonte à la surface, la force^[18] qui pousse en haut ce corps a pour mesure la quantité dont le poids d’un égal volume de liquide surpasse le poids même du corps.

Fig. 5.

En effet, soit un corps Α plus léger^[19] que le liquide. Soit β le poids de ce corps, et β + γ le poids d’un volume de liquide égal à Α. Il s’agit de démontrer que le corps Α, enfoncé de force dans le liquide, remontera avec une force égale à γ.

Prenons un corps Δ, dont le poids soit égal à γ. L’ensemble composé des corps Α et Δ sera plus léger^[19] que le liquide. Car, le poids des deux réunis est β + γ, mais le poids du liquide égal en volume à Α + Δ, serait supérieur à β + γ qui est seulement ce que pèse un volume de liquide égal à Α.

Donc, abandonnons dans le liquide l’ensemble composé des corps Α et Δ. Il y enfoncera jusqu’à ce que le volume de liquide égal à la partie immergée ait le même poids que le corps tout entier. C’est, en effet, ce qu’on vient de démontrer^[20].

[Soit αδ la circonférence formant la surface du liquide.] Puisqu’un volume de liquide égal à Α a le même poids que ΑΔ, il est clair que la partie immergée sera Α, que l’autre partie, c’est-à-dire Δ, émergera tout entière. [Cela étant démontré, le reste de la proposition l’est^[21]]. Il est évident que la force qui pousse Α vers le haut est égale à celle qui pousse en bas la partie supérieure Δ, puisqu’aucune des deux parties n’entraîne l’autre avec elle.

Mais la pesée de Δ vers le bas est précisément le poids γ ; car nous avons supposé le poids de Δ égal à γ. Ce qu’il fallait démontrer est donc évident.

Proposition VII.

Un corps plus lourd que le liquide où on l’abandonne descendra au fond, et son poids, dans le liquide, diminuera d’une quantité mesurée par ce que pèse un volume de liquide égal à celui du corps.

D’abord, il est évident que le corps descendra au fond. Car les parties de liquide qui se trouvent sous lui sont plus pressées que celles qui sont à son niveau^[22], puisque le solide est supposé plus lourd que le liquide. Démontrons maintenant que son poids y diminuera de la quantité que nous avons dite.

Soit en effet un corps Α plus lourd que le liquide, et soient β + γ le poids de Α, β le poids du liquide égal en volume à Α. Il s’agit de démontrer que le corps Α, plongé dans le liquide, aura précisément pour poids γ. Prenons un autre corps Δ plus léger à égalité de volume que le liquide^[23], ayant d’ailleurs pour poids β ; convenons Fig. 6.
qu’un volume de liquide égal à Δ aurait pour poids β + γ L’ensemble composé des corps Α et Δ sera aussi pesant que le liquide. Car le poids des deux réunis est égal à β + γ + β ; mais le poids du volume équivalent de liquide est égal à cette même somme. Par conséquent, si l’on jette et qu’on abandonne ces deux corps réunis dans le liquide, ils y seront en équilibre et ne remonteront ni ne descendront ; car le corps Α, étant plus lourd que le liquide, sera porté en bas, mais ramené aussi en haut, exactement avec la même force, par le corps Δ. Mais le corps Δ, plus léger que le liquide, est porté en haut par une force égale à γ. Car il a été démontré^[24] que les corps solides plus légers que le liquide où on les enfonce remontent à la surface avec une force égale à la différence entre le poids du volume de liquide égal au leur et leur propre poids. Or, le volume de liquide égal à Δ est plus lourd que Δ d’une quantité égale à γ. D’où il résulte que le corps Α est porté en bas par un poids égal à γ.

SECONDE HYPOTHÈSE.

Supposons que tout corps qui, plongé dans un liquide, remonte, est poussé en haut suivant la verticale qui passe par son centre de gravité.

Proposition VIII.

Si un corps solide, ayant la forme d’un segment de sphère, est abandonné dans un liquide, et si la base du segment ne touche pas le liquide, le corps se tiendra droit, et l’axe du segment sera Fig. 7.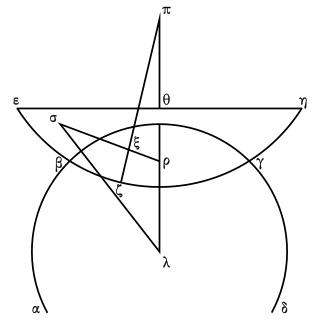
vertical. Et si l’on dérange le solide, de façon à faire toucher le liquide par la base du segment, la figure, dès qu’on l’abandonne de nouveau, ne reste pas penchée, mais reprend sa situation droite.

[Note marginale du traducteur latin de 1269 :

« Il y avait un demi-feuillet blanc. La démonstration de ce théorème manquait dans mon exemplaire grec ; c’était la fin d’un cahier, et au commencement du cahier suivant se trouvaient des figures qui sont, selon moi, celles de ce théorème. »]

Proposition IX^[25].

Par conséquent, si le corps est plus léger que le liquide, et si, quand on l’y abandonne, sa base y plonge tout entière, ce solide se tiendra droit et la direction de son axe sera verticale.

Envisageons un corps, tel qu’on vient de le définir, abandonné dans le liquide. Imaginons aussi un plan mené par la flèche du segment et par le centre de la terre. Soit αβγδ la circonférence que Fig. 8.
forme l’intersection de ce plan avec la surface du liquide, εζη le contour de notre fragment sphérique, et enfin la droite εη.

La flèche du segment étant ζθ, admettons, si toutefois la chose est possible, que ζθ ne soit pas verticale. Il faut montrer que la figure ne gardera pas sa situation, et se redressera.

Le centre de la sphère est sur ζθ. D’abord, supposons le segment plus grand que la demi-sphère. S’il était égal à la demi-sphère^[26], le centre serait en θ, en π s’il est plus petit, en κ s’il est plus grand.

Par κ et le centre de la terre λ, menons la droite κλ. La figure située au-dessus du liquide a son axe sur la verticale qui passe en κ. Pour les mêmes raisons, son centre de gravité est sur la ligne νκ, soit en ρ. Mais le centre de gravité de tout le segment est sur la ligne ζθ, entre κ et ζ, soit en τ. Par conséquent, le centre de l’autre partie de la figure, celle qui plonge dans le liquide, sera sur la droite τρ prolongée^[27]… sera avec τρ dans le même rapport où le poids de la portion de la figure qui émerge est avec celui de la portion immergée. Soit ο le centre de la portion immergée. Par ο, menons la verticale ολ. Le poids de la portion qui émerge se portera en bas suivant la droite ρο ; celui de la portion immergée en haut suivant la droite ολ. Donc la figure ne reste pas dans sa position. Mais les parties situées du côté de η descendent, celles situées vers ε montent, et cela continue jusqu’à ce que la ligne ζθ se trouve verticale.

---

1. Les parties de même niveau. — Les mêmes expressions se trouveront dans les propositions II, III, IV, V et VII. Elles y ont une importance capitale. Le mode de démonstration employé par Archimède consiste à examiner ce qui se passe, pour chacun des cas qu’il envisage, dans une même couche horizontale. La seconde proposition va définir avec précision le niveau ou l’horizontalité d’une couche liquide. Dès lors ces mots auront une signification rigoureusement déterminée qu’ils n’ont pas encore dans cette première hypothèse. Ils n’y désignent que l’horizontalité apparente de l’eau calme. Ch. Thurot (Recherches sur le principe d’Archimède, p. 13) traduit prudemment les mots latins ex æquo jacentibus par « également situées », sans préciser l’égalité dont il s’agit et qui ne peut être qu’une égalité de symétrie (autour d’un point qu’on n’indique pas). Le grec que reflètent ces trois mots est évidemment ἐξ ἴσου κειμένων. C’est une des périphrases par lesquelles le langage ordinaire désignait la direction horizontale, ne possédant aucun mot unique et spécial pour exprimer cette idée. Au reste, voici tout ce passage tel que le donne la vieille traduction latine : « Supponatur humidum habens talem naturam ut partibus ipsius ex æquo jacentibus et existentibus continuis expellatur minus pulsa a magis pulsa, et unaquæque autem partium ipsius pellitur humido quod suprà ipsius existente secundum perpendicularem [si humidum sit descendens in aliquo et ab alio aliquo pressum]. » Voici le grec que, selon les conjectures les plus probables, le traducteur a pu avoir sous les yeux : Ὑποκείσθω τὸ ὑγρὸν ἔχον τοιαύτην φύσιν ὥστε τῶν μερῶν αὐτοῦ ἐξ ἴσου κειμένων καὶ ὄντων συνεχῶν ἐξωθεῖσθαι τὸ ὠθούμενον ἧττον ὑπὸ τοῦ μᾶλλον. Καὶ ἕκαστον δὲ τῶν μερῶν αὐτοῦ ὠθεῖται τῷ ὑπὲρ αὐτοῦ ὄντι κατὰ κάθετον.
2. Et cela lorsque, etc. — Ces mots sont inutiles à l’intelligence de ce qui précède Ils n’y ajoutent rien. Ils ne figurent pas dans la traduction en arabe de 969 (Voir l’Introduction) et il est permis de croire que Mohammed ne les trouvait pas dans son texte grec. Ils paraissent n’être qu’une de ces gloses soi-disant explicatives, mais réellement oiseuses, qui, dans les transcriptions de manuscrits, passent souvent de la marge au texte. M. Heiberg a montré que ces interpolations ne sont que trop fréquentes dans le grec d’Archimède. — Peyrard traduit (librement) : « Soit que le fluide descende quelque part, soit qu’il soit chassé d’un lieu dans un autre ».
3. Déterminé. — Mot à mot : par un point toujours le même.
4. Formant des angles égaux de part et d’autre de κβ. Je ne sais pourquoi, dans la figure de Tartaglia, reproduite par Heiberg, ces deux angles sont inégaux. — D’autre part les lettres qui se rapportent aux points de la figure sont légèrement interverties, ce semble, dans la traduction de 1269, tout à fait mêlées dans Tartaglia ; si bien qu’on ne peut plus suivre la démonstration. Sans changer un mot du texte, je les ai rétablies d’après le sens de l’ensemble, qui est on ne peut plus clair. — Partout j’ai restitué les lettres grecques qui, d’après divers indices, doivent avoir été celles de l’original lui-même.
5. Voir la Note de la page 11.
6. De même volume et de même poids. — C’est-à-dire de même densité : « Archimède, dit Thurot (Recherches, p. 13), démontre facilement qu’un corps de même pesanteur que le liquide où il est abandonné plongera tout entier… À pesanteur il faut ajouter spécifique, expression à laquelle rien ne répond dans Archimède. » Ch. Thurot est sévère. La langue n’avait pas de mot unique et spécial pour exprimer cette notion. Mais nous trouvons ici æqualis molis et æqualis ponderis, plus bas magnitudine æquale et æquè grave supponitur solidum cum humido, expressions que nous serions en droit de traduire par le même poids sous le même volume. Ces périphrases dont nous soulignerons la traduction, chaque fois qu’elles se rencontreront, ne laissent rien à désirer pour la clarté.
7. Mais à ne pas descendre encore plus bas. — Cette seconde assertion n’est pas justifiée ici. L’équilibre du solide pour les déplacements vers le bas n’est physiquement stable que si l’on tient compte de l’augmentation de la densité du liquide avec la profondeur. Or c’est une condition à laquelle on ne voit pas qu’Archimède ait songé. — Cette seconde partie de l’énoncé manque chez le traducteur arabe de 969. Peut-être ne la trouvait-il pas dans son manuscrit.
8. εζηθ le corps flottant. — Le traducteur de 1269 écrit : solidæ magnitudinis insidentia (sic) et avertit en marge qu’il avait dans son texte grec ὄχημα (synonyme évident du participe ὀχούμενον qu’on lit au titre de ce traité), substantif auquel on ne connaissait que le sens de véhicule (ou rarement de bateau).
9. Ajoutons, pour la clarté : de la façon que nous avons supposé les choses, elles ne sont pas également poussées.
10. Thurot résume ainsi cette longue démonstration : « Archimède démontre que le corps plongera tout entier, en établissant que si (le liquide étant supposé immobile) une portion du corps restait au-dessus de la surface, la portion du liquide placée sous le corps serait plus pressée que celle qui est à côté, et le liquide ne serait pas immobile ».
11. La première partie du raisonnement montre que l’équilibre est impossible si le solide n’est pas entièrement immergé ; la seconde que l’équilibre est atteint dès qu’il cesse d’émerger. Mais, d’après le même raisonnement, l’équilibre subsistera à quelque profondeur que ce solide soit plongé. On s’étonne donc de trouver ici cette démonstration accessoire qui ne démontre pas. Est-elle de la même main que ce qui précède ? Voir la Note 1, page 15.
12. Que d’ailleurs. — Ajoutons, pour la clarté : dans ces conditions, …
13. « Peyrard, dit Thurot, est encore ici très inexact, en traduisant (p. 374) un solide Η qui soit composé du fluide. Archimède ne suppose nulle part la solidification d’une partie du liquide. »
14. Égal en volume mais plus léger. — Voir la Note 3, page 14.
15. Ici le texte paraît altéré, déparé par une lacune ; le sens est évident.
16. Ces trois mots, inutiles à tout prendre, manquent de clarté. Le texte grec paraît avoir été mal lu par le traducteur latin.
17. « Logiquement, dit Thurot, cette démonstration indirecte et négative serait irréprochable. Mais elle ne nous montre pas physiquement comment le corps spécifiquement plus léger que le liquide est poussé en haut. Aussi Archimède, avant de traiter de l’équilibre des conoïdes est-il forcé de demander qu’on lui accorde un second postulat. » Voir, plus loin, Hypothèse II.
18. La force qui pousse en haut ce corps. — « Peyrard, dit Ch. Thurot, traduit inexactement vi par vitesse dans le texte de la démonstration. » Voici comment Thurot traduit cet énoncé difficile à formuler brièvement : « Un corps plus léger que le liquide où il est enfoncé de force se relève et est porté en haut avec une force égale à la quantité dont le poids d’une portion de liquide égale au corps surpasse le poids du corps. »
19. Plus léger. — Spécifiquement. Il faut ici sous-entendre cette idée complémentaire, qui n’est rendue d’aucune façon.
20. Ce qu’on vient de démontrer. — Dans la proposition précédente dont celle-ci n’est qu’un corollaire.
21. Cette parenthèse dont nous donnons le sens probable est formée de quelques mots grecs lus de façon incertaine par le traducteur et transcrits tels quels à la marge de son exemplaire, sans qu’il ait tenté de les faire passer en latin. Voir Note 3, page 6.
22. Celles qui sont à son niveau. — « La traduction de Peyrard (p. 376) qui a suivi le texte de Commandin n’est pas claire : « Les parties du fluide qui sont au-dessous sont plus pressées que les parties qui leur sont adjacentes. » Archimède veut dire : « qui sont à la même distance qu’elles du centre de la Terre. » Note de Ch. Thurot (Recherches, p. 14).
23. Plus léger, à égalité de volume, que le liquide. — Levior humnido molis æqualis cum ipsa. Probablement : κουφότερον ὑγροῦ τοῦ ἰσομεγέθους αὐτῷ. La notion de poids spécifique est exprimée ici par une périphrase, mais de la façon la plus explicite.
24. Il a été démontré. — Par la Proposition VI.
25. Proposition IX. — Ce titre ne se trouve pas dans la traduction latine. Peut-être cette proposition suivait-elle, dans le texte grec, la huitième, comme une simple conséquence.
26. S’il était égal à la demi-sphère. — On voit que le texte, tel que nous le donne le traducteur latin, promet l’examen de trois cas et n’en examine qu’un seul. Encore cette démonstration n’est-elle pas très nette. Du reste, une lacune la dépare.
27. La droite prolongée… — Ici une lacune de huit lettres dans la vieille traduction latine. Sans doute : d’une longueur telle qu’elle sera….