Les Rayons alpha, bêta, gamma des corps radioactifs en relation avec la structure nucléaire
LES RAYONS α, β, γ DES CORPS RADIOACTIFS EN RELATION AVEC LA STRUCTURE NUCLÉAIRE
’étude des rayons émis par les substances radioactives
a permis d’aborder pour la première fois d’une
manière concrète, le problème de la structure des
atomes et a ouvert à la science le domaine entièrement
nouveau de la physique nucléaire. Il serait
impossible de décrire ici en détail les propriétés de ces rayons
qui font l’objet d’ouvrages consacrés à la Radioactivité. Ces propriétés
et les méthodes mises en œuvre pour les étudier seront
donc résumées ici, dans la mesure où elles apportent des éléments
d’information relativement à la structure de l’atome et
du noyau atomique.
1. — Les transformations radioactives. Les rayons α, β, γ.
Tout élément radioactif éprouve une transformation atomique, qui atteint successivement les atomes dont il se compose. La transformation consiste soit dans l’émission d’un rayon α, soit dans celle d’un rayon β. Un rayon α est un atome d’hélium doublement ionisé (charge positive), tandis qu’un rayon β est un électron (charge négative). Parmi les électrons émis par les radioéléments, il faut cependant distinguer les rayons β primaires, ou « électrons de désintégration » dont le départ détermine effectivement la transformation de l’atome, et les électrons ou rayons β secondaires qui ne correspondent pas à une modification aussi fondamentale et dont l’émission est liée à celle de rayons γ. Ces derniers sont une radiation électromagnétique émise comme suite de la perturbation produite dans l’atome par l’émission d’un rayon α ou d’un rayon β primaire.
La nature des rayons α a été établie par la mesure de leur déviation dans un champ magnétique et dans un champ électrique, d’où l’on déduit le rapport E/M de la charge à la masse, ainsi que la vitesse v des rayons. La production d’hélium par les radioéléments qui émettent des rayons α est un phénomène qu’on peut suivre quantitativement ; le volume de l’hélium produit est celui qu’on peut prévoir d’après le nombre de rayons α émis dans le même temps et déterminé par une des méthodes de numération applicable à ces rayons. Un atome d’uranium, dans ses transformations successives, libère 8 atomes d’hélium. On est ainsi conduit à penser que l’atome d’hélium entre, comme élément constitutif, dans la structure de l’atome d’uranium et d’autres radioéléments. Cette conception généralisée a été étendue à tous les éléments. D’autre part, la spectrographie des masses, née de la découverte de l’isotopie, a montré que les éléments simples au point de vue isotopique ont des masses très voisines de multiples d’une même masse unitaire, qui est la 16e partie de celle de l’atome d’oxygène et diffère peu de celle de l’atome d’hydrogène. On arrive ainsi à considérer tous les atomes comme composés d’atomes d’hydrogène dont la plupart sont groupés en atomes d’hélium, ce groupement comportant une diminution de masse ou condensation, correspondant à la perte d’énergie interne lors de la constitution du groupement.
2. — Le passage des rayons α par la matière. Parcours. Chocs exceptionnels. L’atome à noyau.
Les rayons α émis par les corps radioactifs forment des groupes homogènes en ce qui concerne la vitesse d’émission. Faisant abstraction du phénomène de « structure fine » dont il sera question plus loin, on peut dire qu’un groupe de rayons α caractérise une substance déterminée. L’énergie initiale de chaque particule s’épuise peu à peu en traversant la matière, dans de nombreux chocs contre les atomes rencontrés ; on peut suivre le trajet tant que la particule possède une énergie supérieure à celle qui est exigée pour l’ionisation. Il a été démontré que ce trajet est très approximativement rectiligne et que les trajectoires de rayons d’un même groupe ont, dans une même matière, des longueurs très peu différentes, groupées par une loi de probabilité autour d’une valeur qui est le parcours le plus probable. La mesure du pouvoir ionisant (nombre d’ions produit par unité de longueur de la trajectoire) d’un faisceau canalisé homogène de rayons α, en divers points de sa trajectoire dans l’air, donne, par ailleurs, la courbe bien connue, représentée dans la fig. 1 ; d’après la pente rectiligne de la partie terminale de cette courbe, on détermine le parcours extrapolé r qui est inversement proportionnel à la densité de l’air. En le rapportant à une densité d’air déterminée (généralement air à 15°, sous la pression normale), on obtient une donnée qui caractérise le groupe homogène considéré. Les parcours des groupes principaux sont compris entre 2 et 9 centimètres. Le parcours augmente avec la vitesse d’émission v, et il existe entre ces grandeurs une relation empirique (loi de Geiger), d’après laquelle r est proportionnel à v². Dans les matières solides ou liquides, les rayons α ont un parcours très petit, atteignant quelques centièmes de millimètres.

Les chocs qui déterminent le ralentissement progressif d’un rayon α, ont, en général, une très faible influence sur sa direction. Certains chocs, dits exceptionnels donnent, cependant, lieu à une brusque déviation qui rejette un rayon d’un faisceau canalise traversant une feuille absorbante très mince (fig. 2).
Cette dispersion des rayons α a conduit Rutherford à la théorie de structure atomique actuellement admise, selon laquelle l’atome se compose d’un noyau central de très petites dimensions, portant une charge positive Ne, et de N électrons distribués autour du noyau, ayant chacun la charge négative e. Le nombre N, nombre atomique, est le numéro d’ordre de l’atome considéré dans la classification périodique des éléments. La situation normale de chaque électron est caractérisée par son niveau d’énergie ou travail qu’il faut dépenser pour l’extraire de l’atome ; ce travail est généralement mesuré en électron-volts. L’atome à noyau a servi de base à la théorie quantique de Bohr qui a donné une interprétation des spectres de raies pour la lumière et pour les rayons X.

Un choc exceptionnel a lieu lorsque un rayon α passe si près d’un noyau atomique qu’il est soumis uniquement à la force de répulsion électrique exercée par celui-ci. En admettant que la force s’exerce selon la loi de Coulomb entre les charges des deux particules Ne et 2e, on peut faire la théorie des déviations exceptionnelles. Si la rencontre a lieu avec un noyau de grande masse, celui-ci n’entre pas en mouvement ; les directions de vitesse de la particule α, avant et après le choc, font entre elles un angle θ tel que , où m est la masse de la particule α, v sa vitesse et b la distance du noyau à la direction de vitesse initiale. La proportion de particules α pour lesquelles la déviation serait supérieure à θ, après passage au travers d’une couche de matière d’épaisseur l, contenant n atomes par unité de volume, est , où b est donné en fonction de θ par la formule précédente. En comptant, par la méthode des scintillations produites sur un écran au sulfure de zinc, les particules α dispersées par unité de surface de l’écran dans une direction θ, on vérifie que leur nombre est en accord avec les prévisions, quand on fait varier θ, N et v. Les expériences faites sur les rayons α de RaC’ traversant des feuilles minces de cuivre, d’argent ou d’or, ont montré que la loi de Coulomb reste applicable à des déviations pour lesquelles b dépasse à peine 10-12 cm.
Quand le choc a lieu contre un noyau léger, celui-ci est projeté avec une certaine vitesse, et le rayon α éprouve une perte d’énergie. Les trajectoires de la particule α et de l’atome projeté, après choc, forment une fourche dont les bras font respectivement les angles θ et θ’ avec la direction primitive du rayon α. Entre ces angles, les vitesses et les masses il existe des relations qui résultent uniquement des principes de conservation de l’énergie et de la quantité de mouvement. Ces relations ont été vérifiées par la méthode des trajectoires de brouillard de Wilson qui permet de photographier des fourches obtenues dans l’air ou autres gaz (hydrogène, hélium, oxygène, argon). Pour calculer la proportion de rayons α dispersés ou d’atomes projetés dans une direction donnée, il faut faire intervenir la loi de force, et on constate alors que les prévisions ne sont pas en accord avec l’expérience. Ce phénomène de dispersion anomale sur les atomes légers a été mis en évidence dans le cas de l’hydrogène, l’hélium, l’aluminium, le magnésium. On arrive à cette conclusion que la loi de Coulomb cesse d’être applicable quand la distance entre la particule α et le noyau est de l’ordre de 4 x 10-13 cm., et que la structure du noyau doit alors intervenir. Les théories proposées pour rendre compte de la dispersion anomale font appel à une force attractive s’ajoutant aux petites distances au terme répulsif conforme à la loi de Coulomb et pouvant résulter totalement ou en partie de la polarisation du noyau (Debye et Hardmeier, Bieler) (voir aussi § 39).
La particule α au moment de son émission est un atome d’hélium doublement ionisé, c’est-à-dire un noyau d’hélium, puisque pour cet élément N = 2. Pendant son parcours dans la matière, elle ne reste pas constamment à cet état, mais peut regagner un électron et le reperdre à nouveau. Vers la fin du parcours elle peut aussi regagner deux électrons et passer à l’état d’atome neutre, d’abord temporairement, puis définitivement.
L’atome d’hydrogène privé de son unique électron est un proton. C’est à cet état qu’il est projeté par un rayon α, lors d’un choc exceptionnel.
Un noyau quelconque peut être considéré comme un assemblage de protons et d’électrons. Une particule α doit, dans ce cas, contenir 4 protons et 2 électrons. Cet assemblage qui paraît très stable, peut faire partie de noyaux plus complexes.
Dans les transformations radioactives, on doit admettre que les particules α et les électrons de désintégration proviennent du noyau, car l’individualité d’un atome est déterminée par le noyau et ne peut être modifiée que par une altération de celui-ci. Les rayons β secondaires proviennent de la région de l’atome extérieure au noyau.
3. — Groupes de rayons α. Spectre magnétique. Structure fine. Loi Geiger Nuttall.
La déviation magnétique des rayons α permet de mesurer le rayon de courbure R de la trajectoire circulaire que décrit un rayon, dans un champ uniforme d’intensité H, normal au plan de la trajectoire. La relation RH = Mv/E donne alors la vitesse si l’on suppose connu le rapport E/M. On admet que celui-ci est donné par la formule Lorentz Einstein E/M = EM0 ; β = v/c est le rapport de la vitesse de la particule à celle de la lumière ; E/M0 est le rapport de la charge E à la masse de repos M0, que l’on admet égal à 4823 unités électromagnétiques. Pour les rayons α, le rapport M/M0 est voisin de 1 et le produit RH est compris entre 2 x 105 et 5 x 105 ; on a environ R = 20 centimètres pour les rayons α de RaC’, si H = 20000 gauss. En raison de cette faible courbure de la trajectoire, la déviation des rayons α a été d’abord étudiée seulement par la méthode directe ; plus récemment la construction du grand électro-aimant de l’Académie des Sciences par A. Cotton a permis d’appliquer la méthode à foyer, grâce à la réalisation d’un champ de grande intensité entre des pièces polaires de 75 centimètres de diamètre, écartées de quelques centimètres. La fig. 3 représente le dispositif de la méthode directe (a) et celui de la méthode à foyer (b) primitivement utilisée pour l’étude des rayons β seulement.
Dans le premier cas, un rayon issu d’une source linéaire étroite S, placée dans un récipient étanche où l’on fait le vide, traverse le diaphragme D et produit sur la plaque photographique P, une raie située en O en absence du champ, en A ou A’ quand il existe un champ normal au plan de la figure. Dans le deuxième cas, le rayon issu de la source S décrit dans le vide une demi-circonférence déterminée par la source S, le diaphragme D et la valeur du champ H, et produit une raie au point F sur la plaque P’. Le point F est un foyer où se coupent les trajectoires de rayons de même vitesse passant par divers points du diaphragme D ; l’image qui s’y forme est donc très nette. Il est facile de voir que le pouvoir séparateur de la méthode à foyer est considérablement plus grand que celui de la méthode directe, les écartements de 2 raies dans ces deux méthodes étant approximativement proportionnels aux déviations qui sont respectivement Z = OA et Z’ = DF.
Dans les dispositifs usuels de déviation directe, Z est de l’ordre de 2 millimètres tandis que Z’ est de l’ordre de 10 à 20 centimètres.

Le spectre magnétique des rayons α obtenu par la méthode directe, à l’aide de sources formées par la matière radioactive sous épaisseur assez faible pour qu’il ne puisse y avoir de ralentissement des rayons dans la matière elle-même, — se compose d’une raie unique pour un groupe de rayons α homogènes caractéristique d’une seule substance. En utilisant la méthode à foyer, S. Rosenblum a trouvé que la raie unique attribuable aux rayons α de ThC n’est pas simple, mais présente une structure fine ; elle se compose de six raies pour lesquelles l’écart extrême des vitesses est environ 4%[1]. L’application de la même méthode a permis d’établir que le groupe émis par AcC est complexe (2 raies), conformément aux résultats obtenus par Rutherford et ses collaborateurs à l’aide d’une méthode d’ionisation différentielle très sensible. On trouve de même une structure complexe dans le cas du radium, du radioactinium, de l’actinium X, de l’actinon.
Parmi les groupes soumis à l’étude, on n’a pas trouvé jusqu’ici de structure fine pour ceux de RaA, RaC’, Po et ThC’.
La détermination de la vitesse permet de calculer l’énergie cinétique d’un groupe de rayons selon la formule
qui, en ce cas, diffère peu de la formule approchée W = ½mv². On a aussi, en électron-volts, W = eV. Prenant, à titre d’exemple, les rayons α de RaC’ dont le parcours dans l’air à 15° est 6,93 cm. et la vitesse 1,922 x 109 cm./sec., on trouve W = 1,2 x 10-5 ergs ou 7,65 x 106 électron-volts.
La mesure précise des parcours offre un moyen pour étudier la complexité de structure de l’émission α. Cette méthode ne donne ni la même précision ni le même pouvoir séparateur que la méthode des spectres magnétiques à foyer. En revanche, elle peut offrir plus de sensibilité pour opérer avec de petites quantités de matière. On l’applique soit en mesurant l’ionisation soit en photographiant les trajectoires de brouillard, soit encore en observant les scintillations produites sur un écran au sulfure de zinc. La vitesse v est reliée au parcours dans l’air par la relation r= Kv³ (K coefficient constant), tant que r > 2 cm. Au-dessous de cette valeur, la relation est modifiée ; des formules empiriques qui l’expriment ont été données par Briggs, par I. Curie et par Blackett.
La mesure des parcours par la méthode d’ionisation est rendue particulièrement sensible quand on laisse pénétrer les rayons au travers de deux chambres d’ionisation étroites A et B juxtaposées, formées par 3 plateaux parallèles très rapprochés ; les rayons pénètrent dans ces chambres au travers de fenêtres ménagées dans les deux premiers plateaux et fermées par des feuilles d’or extrêmement minces. À l’aide d’un amplificateur puissant, on mesure l’excès du courant d’ionisation produit dans la chambre A sur celui produit dans la chambre B. On décèle ainsi un très petit nombre de rayons dont le parcours a pris fin dans la chambre A. C’est par cette méthode que Rutherford et ses collaborateurs ont découvert la complexité des rayons α de RaC et de AcC.
La mesure du parcours à l’aide des trajectoires de brouillard fait intervenir la fluctuation de parcours dont l’importance approchée est de l’ordre de 1 à 2 % du parcours le plus probable. On détermine celui-ci par un dénombrement des trajets compris entre des limites données. C’est ainsi qu’Irène Curie a établi que les rayons α du radioactinium forment 2 groupes dont les parcours diffèrent de 3 mm. 4, résultat en accord avec d’anciennes expériences de S. Mayer et Paneth. L’emploi de la méthode à foyer a permis de découvrir dans ce cas une structure plus fine encore ; dans le spectre magnétique chacun des deux groupes mentionnés se montre complexe, et on trouve en plus, quelques raies faibles.
La méthode des scintillations, fréquemment employée pour la mesure des parcours, a permis de découvrir, à côté des groupes normaux de rayons α de RaC’ et de ThC’, des groupes dits de « long parcours », se composant d’un nombre de rayons relativement très petit. Ces rayons de long parcours ont aussi été mis en évidence par la méthode des trajectoires de brouillard et par celle d’ionisation différentielle. Pour quelques-uns de ces groupes faibles, S. Rosenblum a récemment obtenu la raie du spectre magnétique. On compte, au total, 9 groupes de rayons de long parcours attribués à RaC’, avec des parcours à 13° compris entre 7,87 et 11,64 cm. et des nombres de rayons compris entre 0,2 et 17 pour 106 rayons normaux de parcours 6,95 cm. Pour Th (C + C’), on a caractérisé 2 groupes de rayons de parcours 9,78 cm. et 11,66 cm., avec respectivement 0,34 et 1,9 rayons pour 104 rayons normaux de ThC’ de 8,62 cm. de parcours.
En résumé, le rayonnement α des corps radioactifs est plus complexe qu’on ne l’avait cru précédemment. Il comprend soit un seul groupe normal, soit plusieurs groupes normaux de vitesses voisines. Peuvent être présents en plus des groupes de long parcours dont l’intensité, mesurée en nombre de rayons émis par atome transformé, est très faible par rapport à celle des groupes normaux, dont l’ensemble, pour un radioélément donné, doit correspondre approximativement à un rayon α émis par atome transformé.
Le nombre de rayons α dans un groupe est connu d’après des méthodes de numération qui décèlent l’effet individuel d’un rayon α. On utilise le plus fréquemment, soit les scintillations produites par les rayons sur un écran au sulfure de zinc, soit l’effet ionisant enregistré par des compteurs électriques dont on a établi de nombreux modèles, et dont certains font appel à une amplification par ionisation par choc, tandis que d’autres utilisent seulement des amplificateurs de grande puissance.
Geiger et Nuttall ont signalé une relation qui existe entre le parcours r d’un groupe de rayons α et la constante λ qui mesure la vitesse de transformation. Portant log r en abscisses et log λ en ordonnées, ils ont obtenu 3 graphiques à peu près rectilignes correspondant réciproquement aux 3 familles d’uranium radium, de thorium et d’actinium. Les parcours utilisés étaient les parcours normaux, abstraction faite de la structure fine. Quelques corps paraissent faire exception, même si l’on recherche seulement une courbe d’allure régulière, en renonçant à la rendre strictement rectiligne.
La loi Geiger Nuttall établit une relation entre la probabilité de la transformation radioactive et l’énergie du rayon α émis ; elle a fait l’objet d’une théorie proposée par Gamow sur laquelle nous reviendrons plus loin.
4. — Composition du rayonnement β. Groupes et spectre continu. Électrons de désintégration. — Les rayons β des corps radioactifs n’ont pas, en général, comme les rayons α un trajet rectiligne dans la matière, car, à vitesse égale, ils sont bien plus facilement déviés de leur direction lors de rencontres avec les noyaux d’atomes et même avec les électrons. Seuls, les électrons très rapides suivent dans l’air des trajectoires rectilignes mises en évidence dans une chambre à détente de Wilson. Tous ceux qui ont une vitesse modérée suivent un chemin sinueux. À une vitesse donnée correspond un parcours moyen, dont la détermination n’est pas précise, car la fluctuation de parcours est relativement importante. Ce parcours qui est de l’ordre du centimètre dans l’air de densité normale pour un électron dont l’énergie est environ 20.000 électron-volts, atteint 12 à 13 mètres pour des électrons de 3 x 106 électron-volts.
L’analyse des rayons β dans un champ magnétique a été faite par la méthode de déviation directe et par la méthode à foyer (fig. 3). Elle a révélé que les spectres magnétiques obtenus pour différentes substances radioactives sont très différents, pouvant se composer d’un spectre continu et de raies plus ou moins nombreuses. Pour Ra, RaD, Rth, on observe quelques raies seulement ; pour RaE, le spectre continu est surtout apparent. Pour les corps qui composent les dépôts actifs : RaB, RaC, etc., de même que pour RaAc et AcX on observe un spectre continu important et un grand nombre de raies (plus de 50 pour RaC). Les limites de vitesse varient également beaucoup d’un corps à l’autre. L’énergie, inférieure à 100 électrons-kilovolts pour les rayons β de RaD ou de Rth, atteint 3.000 él.-kv. pour ceux de RaC. On a même observé chez RaC, ThC″ et Mth2 l’émission de rayons β de très grande énergie sous forme de faibles raies ou bandes signalées par Yvanovitch et d’Espine au-dessus de 2.500 él.-kv., jusqu’à 11.000 él.-kv.
Les travaux de nombreux auteurs ont montré que les raies des spectres magnétiques correspondent à des rayons β d’origine secondaire, déjà signalés précédemment, tandis que les électrons de désintégration qui proviennent du noyau paraissent former le spectre continu. On est donc conduit à admettre que la désintégration d’un noyau par perte d’un électron nucléaire ne correspond pas pour celui-ci à une vitesse déterminée, comme cela a lieu pour un rayon α, mais qu’au contraire les électrons de désintégration d’une même substance sont émis avec des vitesses variables dans de larges limites. Cette circonstance constitue une difficulté théorique considérable. Il est aussi très remarquable que, pour certains radioéléments, les électrons de désintégration ont une énergie si faible qu’on ne les a pas encore identifiés jusqu’à présent (Ac, Mth1).
La nature de la transformation ne peut cependant pas être mise en doute, car les propriétés chimiques de l’atome résultant de la transformation et sa place dans le système périodique sont bien celles qui correspondent à la perte d’un électron nucléaire, c’est-à-dire à l’augmentation d’une unité pour le nombre atomique.
Le spectre continu des rayons β a été étudié par des méthodes de numération de ces rayons, le récepteur pouvant être un compteur électrique, dans lequel on reçoit les rayons issus d’une source S et déviés dans un champ magnétique comme dans la fig. 4. Les courbes de distribution de l’intensité i dans le spectre continu, en fonction de l’énergie W des rayons offrent le même type général : i augmente d’abord avec W, passe par un maximum, puis décroît et tend vers 0 quand W continue à augmenter (fig. 5). La limite du spectre continu correspond à une
énergie d’autant plus élevée que la vie de la substance est plus courte. Les raies apparaissent comme des maxima aigus superposés à la courbe représentative du spectre continu.


L’absorption des rayons β dans la matière est caractérisée par le parcours ou, plus fréquemment, par le coefficient d’absorption

entre la source et la chambre, un écran absorbant d’une épaisseur x.
Le coefficient μ diminue rapidement quand la vitesse des rayons augmente ; pour des rayons de vitesse donnée, son quotient μ / ρ par la densité augmente un peu avec le nombre atomique[2].
5. — Absorption du rayonnement γ. Groupes homogènes. Diffusion nucléaire.
Le rayonnement γ des corps radioactifs a été d’abord caractérisé par la méthode d’absorption, l’intensité des rayons étant mesurée dans une chambre d’ionisation comme dans la fig. 6. Les rayons β sont, en ce cas, déviés par un champ magnétique. Quand il s’agit de mesures précises, on utilise un faisceau canalisé, et on distingue, comme pour les rayons X, le coefficient d’absorption photoélectrique τ et le coefficient de diffusion . Le coefficient total étant μ, on a , où . Les lois numériques appliquées aux coefficients τ et sont celles qui ont été établies
pour les rayons X. Le coefficient τ qui est prédominant dans l’absorption des rayons X ou γ de faible fréquence, augmente très rapidement avec la longueur d’onde λ de ces rayons et avec le nombre atomique de la matière absorbante ; il subit une variation brusque pour chaque valeur de λ qui correspond à un niveau d’absorption de la matière considérée. Le coefficient a une
importance relative d’autant plus grande que la longueur d’onde est plus petite et les atomes absorbants plus légers. Le calcul théorique de ce coefficient a été donné par J. J. Thomson sur la base de la théorie électromagnétique classique, d’après laquelle un électron contenu dans un atome entre en vibration sous l’influence de l’onde qui passe sur lui, et par là, empruntant de l’énergie à cette onde, est une source de réémission d’ondes semblables dans l’espace environnant. À cette diffusion sans changement de longueur d’onde vient s’ajouter la diffusion avec changement de longueur d’onde découverte par A. H. Compton et accompagnée
d’une projection des électrons diffusants. D’après la théorie de l’effet Compton, le coefficient est de la forme , où est le coefficient de J. J. Thomson répondant à la formule
(e charge de l’électron en unités E. S., m sa masse de repos, n nombre d’électrons par unité de volume, c vitesse de la lumière) ; α est un paramètre défini par la relation où h est la constante de Planck et υ la fréquence de la radiation. La fonction égale à 1 pour α = 0, décroît quand α augmente et s’annule pour α = ∞. La théorie de l’effet Compton fait appel aux notions de quanta, la diffusion étant considérée comme un choc entre un quantum de radiation, et un électron. Attribuant au quantum l’énergie et la quantité de mouvement , à l’électron l’énergie et la quantité de mouvement ( rapport de la vitesse v de l’électron à

celle de la lumière), on peut écrire les équations de conservation de l’énergie et de la quantité de mouvement. Au quantum primaire correspond après le choc, un quantum diffusé dans la direction θ et un électron projeté dans la direction φ, les quantités υ’, φ et W étant définies en fonction de θ (fig. 7). Pour calculer le coefficient de diffusion il est de plus nécessaire de définir la
probabilité pour que le quantum primaire soit diffusé dans la direction θ. La formule , trouvée par Compton pour résulte de considérations basées à la fois sur la théorie des quanta et sur la théorie classique. Plus tard, Klein et Nishina ont donné à une forme plus compliquée, résultant de l’application des méthodes de la mécanique ondulatoire. L’énergie soustraite au faisceau par le processus de diffusion se partage entre les quanta diffusés et les électrons de choc.
Le coefficient τ a également reçu une interprétation quantique. On admet qu’il caractérise un processus d’absorption, dans lequel un quantum cède intégralement son énergie à un atome, en produisant l’ionisation de celui-ci dans un de ses niveaux. Si Wi est le travail d’extraction de l’électron du niveau i, sur lequel porte l’ionisation, et W l’énergie cinétique de l’électron extrait, on a la relation d’Einstein .
La mesure du coefficient d’absorption des rayons γ émis par les radioéléments permet de caractériser des groupes de ces rayons qui correspondent à des coefficients définis. Plusieurs groupes peuvent appartenir à une même substance radioactive. On détermine le coefficient d’absorption dans l’aluminium, et pour les rayons très pénétrants, dans le plomb. Ces coefficients sont compris entre de larges limites ; en les comparant à ceux qui ont été mesurés pour des rayons X de longueur d’onde connue, on reconnaît que certains groupes de rayons γ sont des groupes de fluorescence émis dans les atomes des radioéléments (ou dans les supports), comme effet secondaire, tandis que d’autres groupes doivent être d’origine nucléaire. Le coefficient d’absorption dans Al qui peut dépasser 1000 cm-1 pour les groupes secondaires, descend au-dessous de 0,1 cm-1 pour les plus pénétrants des rayons γ nucléaires.
Quand plusieurs groupes homogènes de rayons γ sont émis simultanément, l’analyse des courbes d’absorption permet de les mettre séparément en évidence. L’influence relative des termes d’absorption photoélectrique et de diffusion dépend, pour chaque groupe, de la longueur d’onde, de la nature de l’absorbant et du dispositif expérimental employé. Dans le domaine où les deux termes ont une importance comparable, le contrôle de leurs relations avec la longueur d’onde rencontre des difficultés considérables.
Par contre, la méthode d’absorption a été très utilement appliquée à l’étude des rayons γ « mous » (de grande longueur d’onde) et à celle des rayons γ très pénétrants (de petite longueur d’onde).
Dans le premier cas, l’absorption photoélectrique intervient pratiquement seule. En employant comme absorbant l’aluminium dont le niveau K correspond à 1.550 volts (), on obtient une variation continue de μ avec λ pour toutes les valeurs de λ inférieures à λk. On a caractérisé ainsi l’émission de groupes de rayons γ dont les fréquences sont du domaine des rayons X, et dont certains sont d’origine nucléaire tandis que d’autres représentent le rayonnement de fluorescence qui accompagne l’émission de rayons α ou β de désintégration, et qui peut prendre naissance soit dans les atomes de la substance radioactive elle-même, soit dans le support sur lequel elle est déposée.
Pour les rayons γ de haute fréquence, l’absorption photoélectrique
est négligeable dans un absorbant à atomes légers, mais dans un élément à nombre atomique élevé, tel que le plomb, les effets d’absorption et de diffusion sont encore du même ordre pour les rayons γ durs de RaC (λ ≥ 20 U. X). On admet, en général, que tous les électrons extranucléaires sont équivalents au point de vue de la diffusion des rayons γ durs. Le coefficient de diffusion par électron mesuré dans une matière à atomes légers, est directement comparé à celui que prévoit la théorie.
Pour cela, le faisceau canalisé de rayons γ, issu de la source S,
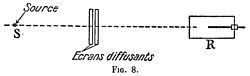
est reçu, sous un angle solide aussi petit que possible, dans un
appareil de mesures R à distance de S, et les écrans diffusants sont placés entre la source et le récepteur (fig. 8). Les radiations à étudier n’étant pas homogènes, on les soumet à une filtration
préalable qui a pour objet d’éliminer les composantes plus molles.
On apprécie la valeur de λ pour cette radiation filtrée, d’après
les données fournies par la spectrographie des rayons γ. Plusieurs
auteurs : Skobelzyn, Chao, Tarrant, Gray, L. Meitner et Hupfeld, Jacobsen ont ainsi comparé la valeur de par électron avec la valeur déduite de la formule Klein Nishina. Les résultats de ces mesures délicates font prévoir que, l’accord avec la théorie paraît satisfaisant pour λ voisin de 7 U. X., mais que pour λ = 4,7 U. X (rayons γ fortement filtrés de ThC″), l’accroissement du coefficient avec le nombre atomique de l’absorbant ne peut s’expliquer entièrement par une part d’absorption photoélectrique. Ceci conduit à envisager un effet de diffusion nucléaire qui, pour le plomb, atteindrait 40 % de l’effet de diffusion normal sur les électrons extranucléaires.
6. — Mesure de la longueur d’onde. Relations entre les rayons β et les rayons γ..
a) Spectres de diffraction. — La méthode de diffraction sur un cristal tournant, appliquée aux rayons γ (Rutherford et Andrade, J. Thibaud, M. Frilley) a permis de révéler l’existence d’un spectre de lignes qui, dans les expériences les plus récentes de Frilley, comprend les rayons γ de RaB et RaC jusqu’à λ = 16 U. X. hυ = 770 eKV. Pour ces rayons, l’angle de diffraction sélective sur le sel gemme n’est plus que 10’, et il parait difficile d’atteindre ainsi les longueurs d’onde plus petites encore. Le spectre se compose de raies dont certaines sont attribuables à des radiations d’origine nucléaire tandis que d’autres correspondent à des radiations de fluorescence excitées dans les atomes qui résultent de la transformation radioactive ; ainsi, dans le spectre des rayons γ de Ra(B + C) on observe les raies de fluorescence de la série L, caractéristiques des éléments de nombres atomiques 83 et 84, ceux qui résultent respectivement de la transformation de RaB (N = 82) et de RaC (N = 83). Les expériences de diffraction prouvent que le caractère ondulatoire des rayons γ reste valable dans le domaine des hautes fréquences.
b) Spectres corpusculaires obtenus par l’effet photoélectrique des rayons γ sur les atomes étrangers. — Un rayon γ d’énergie hυ, émis par un atome radioactif, peut subir l’absorption photoélectrique dans un atome étranger, en donnant naissance à un rayon β dont l’énergie est W − hυ − Wi, où Wi est une énergie de niveau de l’atome absorbant. Ainsi a lieu la conversion externe du quantum hυ en un rayon corpusculaire. Si les énergies de plusieurs photoélectrons issus de divers niveaux, vérifient la relation W + Wi = constante, on peut estimer qu’il existe un groupe de rayons γ qui donne naissance aux photoélectrons considérés. Pour mesurer W on a recours à la méthode des spectres magnétiques corpusculaires, avec un dispositif tel que celui de la fig. 3 b où la source S est entourée d’un très mince écran absorbant dans lequel sont libérés les photoélectrons. Les travaux d’Ellis et de J. Thibaud ont montré que cette méthode permet d’identifier dans le rayonnement γ des corps radioactifs, des groupes monochromatiques d’énergie déterminée, et J. Thibaud a étendu cette démonstration aux groupes de haute fréquence émis par les dérivés du radium et du thorium, pour lesquels il n’a pas été possible jusqu’à présent d’obtenir le spectre de diffraction.
c) Spectres corpusculaires obtenus par l’effet Compton produit par les rayons γ sur les atomes légers. — La projection d’électrons par les rayons γ qui subissent l’effet Compton, offre un autre mode de conversion externe de l’énergie de ces rayons. Quand les atomes absorbants sont légers, on peut estimer que ce processus se produit seul, les liaisons atomiques des électrons ayant une importance négligeable. Skobelzyn a basé sur ce principe une méthode statistique de spectrographie de rayons γ. Un faisceau de ces rayons est envoyé dans une chambre à détente Wilson qu’il traverse suivant une horizontale. Les électrons de choc, produits dans l’air de la chambre et animés de la vitesse v, s’enroulent suivant des circonférences ou des hélices dans un champ magnétique vertical. Ces trajectoires électroniques sont photographiées à l’aide d’un dispositif stéréoscopique. Entre l’énergie hν du quantum primaire, l’énergie W de l’électron et l’angle φ que fait la direction initiale de sa vitesse avec celle du faisceau γ primaire, on a la relation suivante dans laquelle α est le paramètre de Compton :
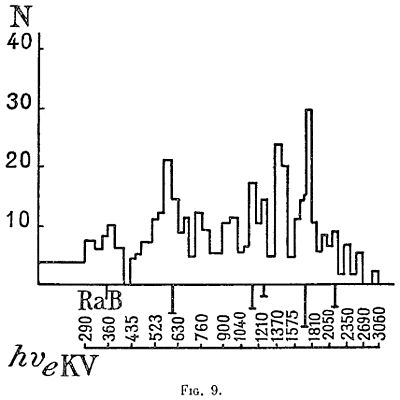
La valeur de W se déduisant du rayon de courbure R de la trajectoire dans un champ H, on peut déterminer hν par la mesure de R et de φ. À l’aide de nombreux clichés contenant chacun plusieurs trajectoires, on peut établir une statistique du nombre relatif N des rayons γ de diverses fréquences qui ont subi l’effet Compton dans la chambre à détente. Cette statistique, confrontée avec les prévisions théoriques basées sur la formule de Klein et Nishina, s’est montrée en accord assez satisfaisant avec la théorie pour les rayons γ de RaC, tandis que pour ceux de Th (C + C″), il paraît y avoir un écart. Dans la figure 9 on a représenté la distribution d’intensité dans le spectre des rayons γ, pour RaB et RaC, d’après la statistique de Skobelzyn.
d) Spectre naturel des rayons β émis par les corps radioactifs. — Le spectre naturel magnétique des rayons β contenant, en général, des raies superposées à un fond continu, l’émission des groupes isocinétiques qui correspondent à ces raies a été interprêtée comme effet secondaire photoélectrique des rayons γ émis dans la même transformation radioactive. L’absorption de ces derniers se produit, en ce cas, dans l’atome qui leur a donné naissance (conversion interne). Chaque groupe de rayons γ peut donner lieu, par conversion interne, à la production de plusieurs groupes d’électrons secondaires, issus de divers niveaux de l’atome.
La transformation radioactive de l’atome étant caractérisée par
l’émission d’un rayon α ou d’un rayon β nucléaire, l’émission de
rayons γ, consécutive à ce phénomène primordial, accompagne le réarrangement interne du noyau après la perturbation. L’émission
de photoélectrons secondaires étant elle-même consécutive à celle des rayons γ, on doit admettre que ces électrons sont extraits des niveaux de l’atome transformé et non pas de ceux de l’atome primitif. Ce point de vue admis par L. Meitner et confirmé par de
nombreux travaux, sert de base pour déduire les énergies des rayons γ de celles des rayons β secondaires faisant partie du spectre magnétique naturel. L’étude de ces derniers a été faite par de nombreux auteurs. Parmi les travaux récents, les plus étendus sont ceux d’Ellis, Black, Hahn et Meitner. L’émission de rayons γ est le plus souvent liée à une transformation radioactive
par émission d’un rayon β, mais on trouve aussi de nombreux groupes de rayons γ dans la transformation de RAc et de AcX qui a lieu avec émission de rayons α.
e) Résumant les résultats des méthodes a, b, c et d, on constate qu’il y a entre eux un accord général donnant une grande valeur à l’ensemble. La spectrographie des rayons γ est ainsi solidement établie, en ce qui concerne la fréquence des groupes monochromatiques. Moins nombreuses sont les données relatives à
leur intensité. Le nombre de groupes d’origine nucléaire est très
variable suivant les substances ; ainsi, on en a défini 15 pour RaC,
et un seulement pour Ra ou pour RaD. À ces groupes viennent
s’ajouter ceux de fluorescence auxquels correspondent également des photoélectrons dans le spectre naturel. L’énergie des groupes
nucléaires est comprise entre des limites étendues, les énergies
les plus élevées étant atteintes pour les corps qui se transforment
avec émission de rayons β sans que cependant on ait trouvé des
groupes d’énergie supérieure à celle des électrons de désintégration
les plus rapides (limite du spectre continu). Les énergies
les plus élevées jusqu’ici mesurées sont celles des groupes 2219 eKV de RaC et 2650 eKV de ThC″.
7. — Relations entre les rayons α et les rayons y. Niveaux nucléaires.
On a vu qu’à l’émission de rayons β nucléaires succède généralement celle de rayons γ nucléaires qui peuvent se manifester soit directement, soit par conversion interne ou externe en rayons β secondaires. Un effet analogue a été observé, pour certains radioéléments, qui émettent des rayons α, et on a reconnu que des relations énergétiques d’importance fondamentale existent entre les énergies des groupes monochromatiques de rayons γ et la structure fine des rayons α. Ce fait, entrevu d’abord par Feather, a été clairement mis en évidence par la mesure précise des vitesses de groupes complexes de rayons α.
Une série d’expériences, particulièrement démonstrative, a été faite sur les rayons α de ThC (Rosenblum et Valadarès). La mesure des vitesses pour les 6 groupes de rayons α de cette substance, permet de calculer leurs énergies W ; entre celles-ci, corrigées de l’effet de recul, on peut former 15 différences énergétiques Δ, concordent numériquement avec les énergies U des groupes de rayons γ nucléaires émis par ThC et ses dérivés.
Pour effectuer la correction qui tient compte de l’énergie W′ de recul de l’atome transformé, on fait porter la différence Δ non sur les valeurs de W mais sur celles de W + W′. Les nombres ainsi obtenus sont indiqués ci-dessous en électron-kilovolts, pour quelques valeurs de Δ et U.
| Δ | 40,6 | 128 | 146 | 166 | 291 | 295 | 332 | 437 | 477 | 585 | 627 |
| U | 40,8 | 128 | 145 | 163 | 292 | 292 | 332 | 439 | 479 | 590 | 627 |
Des concordances semblables apparaissent entre les rayons α et γ, dans le cas du radioactinium, de l’actinium C et du radium.
Gamow a interprété ces remarquables coïncidences, en admettant qu’après le départ du rayon α de désintégration, le noyau résiduel se trouve à l’état normal si le rayon α a été émis avec l’énergie maximum ; si, au contraire, le rayon α a été émis avec une énergie réduite, c’est que le noyau a absorbé une partie de l’énergie de désintégration et se trouve à l’état excité. On peut concevoir que le noyau possède des niveaux d’énergie, et que l’excitation du noyau correspond au transfert d’une particule constituante d’un niveau à un autre, plus élevé. Selon Gamow, les particules qui interviennent dans ce transfert seraient les particules α constitutives du noyau[3]. Un atome excité revient spontanément à l’état normal par l’émission d’un groupe de rayons γ (ou de plusieurs groupes consécutifs), d’où égalité énergétique entre les quantités Δ et U. Dans cette manière de voir, il y aurait à considérer autant de niveaux d’énergie nucléaires que de groupes de rayons α distincts, et les énergies de ces niveaux seraient de la forme , étant l’énergie du niveau normal, et étant la différence énergétique entre le groupe normal de rayons α et un groupe de moindre énergie d’ordre n. Par exemple, les 6 groupes de rayons α du ThC correspondraient aux niveaux , en électron-kilovolts.
Il importe de rappeler ici que les rayons γ sont émis après la transformation radioactive comportant l’émission de rayons α (ou de rayons β), c’est-à-dire dans le noyau transformé. Si, comme il est probable, le noyau ne persiste pas longtemps dans l’état excité, l’émission de rayons γ aurait lieu au début de la vie de l’atome transformé. Par exemple, si une substance A émettant des rayons α (ou β) se transforme en B, les rayons α (ou β) sont émis par les atomes A à la fin de leur vie, les rayons γ par les atomes B au début de leur vie, — mais les uns et les autres font partie des événements qui caractérisent la transformation de A en B. Dans le langage courant actuel les rayons primaires α ou β et les rayons γ consécutifs sont tous attribués au corps A. Pour éviter toute confusion, on peut convenir de les attribuer à la transformation A → B.
L’interprétation ci-dessus exposée de la relation entre les rayons α et les rayons γ, doit, semble-t-il, s’appliquer précisément aux rayons émis dans une transformation donnée. Tel est le cas de RAc, où la concordance numérique a lieu entre les rayons α de RAc et les rayons γ attribués au même élément (c’est-à-dire émis par les atomes d’AcX résultant de la transformation RAc → AcX, au début de la vie des atomes transformés). Dans le cas de ThC, apparaît une complication : alors que les rayons α sont émis dans la transformation ThC → ThC″, les rayons γ, avec lesquels ils sont en relation, étaient jusqu’à ces derniers temps attribués à ThC″, c’est-à-dire à la transformation ThC″ → ThD. Autrement dit, l’énergie disponible en raison de l’excitation initiale du noyau ThC″ ne serait pas libérée pendant l’existence de celui-ci, mais après sa transformation en ThD avec la modification correspondante des niveaux nucléaires, et sans doute aussi des états d’excitation. Il y avait là une difficulté pour la théorie ; et il était désirable de soumettre à un contrôle précis l’origine des rayons γ émis par Th(C + C′ + C″). Le même problème se pose pour Ac(C + C″) (AcC′ ayant ici une importance secondaire en raison de sa faible proportion). Tout récemment Ellis et Sze-Shih-Yuan indépendamment, ont pu préciser l’origine de plusieurs groupes λ émis par Th(B + C + C′ + C″). Un certain nombre de ceux-ci que l’on associait à la transformation ThC″ → ThD sont en fait émis lors de la transformation ThC → ThC″, et ces groupes sont précisément ceux qui correspondent à l’une des égalités Δ = U, ci-dessus signalées. Ainsi, la difficulté d’interprétation disparaît. Il faut voir dans ces faits une preuve très satisfaisante de l’association des groupes α et γ émis par un même élément.
D’après Gamow, l’émission de rayons α de long parcours serait
également en relation avec un état d’excitation du noyau. Par
exemple, dans la transformation RaC → RaC′ ou ThC → ThC′, avec émission d’un rayon β nucléaire, le noyau résultant RaC′ ou ThC′ serait formé à l’état excité C′e, c’est-à-dire qu’une des particules α constituantes pourrait y occuper un des niveaux d’énergie supérieurs En. Le noyau excité C′e aurait la faculté de revenir à l’état normal par émission d’un quantum γ de fréquence ν, et de subir
ensuite une transformation normale C′ → D, avec émission d’un rayon α de parcours normal r0 (fig. 10). La probabilité θ de cette

transition serait très grande. Mais il existe aussi une certaine probabilité λ pour que C′e se transforme directement en D, en émettant une particule α de long parcours r, la différence énergétique Δ qui correspond à la différence des parcours étant égale à hν. Le
nombre N de rayons de long parcours (pour abréger, rayons lp),
par atome transformé serait donné par la formule
où
p est la proportion d’atomes C′ qui se forment à l’état excité, tandis que le nombre de quanta par atome transformé est p − N.
On a aussi . On peut étendre le schéma de la fig. 10 au cas de plusieurs groupes de rayons lp et de plusieurs groupes
de rayons γ, correspondant à des états d’excitation différents, relatifs à divers niveaux nucléaires.
Si ces prévisions sont exactes, les différences énergétiques entre les groupes lp et le groupe normal (corrigées de l’effet de recul) doivent correspondre aux groupes de rayons γ émis respectivement dans les transformations RaC → RaC′ et ThC → ThC′.
Parmi les 9 groupes de rayons lp, attribués par Rutherford, Ward et Lewis à RaC′, on en trouve 3 (parcours à 15° respectivement 7,87 cm., 9,60 cm. et 10,31 cm.), pour lesquels les excès d’énergie par rapport au groupe normal de parcours 6,95 cm. paraissent correspondre à 3 groupes importants de rayons γ dont les énergies en eKV sont respectivement 612, 1778, 2219.
Le groupe lp le plus important, parcours 9,13 cm., parait pouvoir être mis en relation avec un groupe de rayons γ de 1426 eKV, sur l’existence duquel, comme tel, l’accord n’est cependant pas établi. En effet, son identification repose sur la présence d’importants groupes de photoélectrons correspondants (extraits des niveaux K, L et M), dans le spectre naturel des rayons β de RaC ; dans la distribution spectrographique obtenue par Skobelzyn, ce groupe paraît intervenir aussi, mais avec peu d’importance, pour extraire des électrons par effet Compton. D’autre part, J. Thibaud n’a pas réussi à obtenir, par conversion externe, des photoélectrons attribuables à ce groupe. Il paraît donc certain qu’en ce cas, l’émission de rayons γ est sinon supprimée, tout au moins fortement désavantagée par rapport à l’effet de conversion interne.
On est ainsi conduit à envisager l’émission de photoélectrons extranucléaires comme un effet pouvant provenir directement d’une interaction entre ces électrons et le noyau, sans l’intermédiaire d’une radiation (R. Fowler) ; il n’y aurait donc pas entre le noyau et les électrons qui l’entourent une indépendance poussée aussi loin qu’on l’a cru primitivement.
Les deux groupes lp émis par ThC′ (parcours 9,78 et 11,66 cm.) ne paraissent pas correspondre aux groupes de rayons γ émis par Th(C + C′ + C″). L’interprétation proposée dans le cas de RaC n’est donc pas valable ici, d’où pour la théorie une complication à résoudre ultérieurement.
De la relation N/(p − N) = λ/θ, admise pour les rayons lp de RaC′, on peut déduire θ, si N et p − N sont donnés par l’expérience, λ étant calculé par extrapolation de la loi Geiger Nuttall, ou mieux par la théorie de Gamow basée sur la mécanique ondulatoire. Les éléments de ce calcul étant encore imparfaitement connus, on ne peut obtenir actuellement pour θ qu’un ordre de grandeur. Voici, d’après Rutherford et Ellis, les valeurs correspondantes de N, λ et θ :| Énergie des rayons γ en eKV |
N | λ | θ |
| ––––––– | ––– | ––– | ––– |
| 612 | 0,49 × 10-6 | 8,1 × 107 | 1,1 × 1014 |
| 1778 | 0,53 × 10-6 | 5,5 × 1010 | 2,7 × 1016 |
| 2219 | 0,60 × 10-6 | 3,5 × 1011 | 4,2 × 1016 |
Les mêmes auteurs proposent l’emploi de 3 coefficients a, g et b pour caractériser les probabilités d’émission respectives d’un rayon lp, d’un quantum ou d’un électron extranucléaire. Les nombres respectifs des émissions par atome transformé étant A, G et B, on aurait les relations : G/A = g/a ; B/A = b/a, permettant de déduire g et b de l’expérience, dans la limite des possibilités actuelles. Le coefficient b serait de l’ordre de 1011 à 1013 sec-1 pour les transitions de 612 eKV à 2219 eKV. Un certain nombre de raies faibles dans les spectres de rayons β naturels, auxquelles on n’a pu faire correspondre de groupes de rayons γ, pourraient résulter de transitions ayant une faible valeur du coefficient g.
L’examen détaillé des rayons γ de RaC a conduit Rutherford et Ellis à exprimer les énergies de ces rayons par la formule , où p et g sont des nombres entiers, tandis que E1 et E2 sont des énergies déterminées. Pour E1 on envisage deux valeurs possibles, 612 et 671 eKV, considérées comme des énergies de niveaux. À E2 on attribue une valeur voisine de 40 eKV, mais un peu différente selon l’une des 6 catégories en lesquelles sont classés les 49 groupes de rayons γ. Les valeurs 1, 2, 3, 4 que peut prendre p, sont interprétées comme indiquant le nombre de particules α dont le passage d’un des niveaux E1 au niveau normal détermine l’émission de rayons γ. Les valeurs attribuées à q varient de 0 à 14. Sur un graphique, où q est porté en abscisses et E en ordonnées, les groupes de rayons γ se distribuent sur 6 lignes droites d’inclinaison voisine. On interprète E2 comme une énergie d’interaction des niveaux.
J. Thibaud a examiné la possibilité d’une relation entre les rayons α et les rayons γ, résultant de l’état de rotation du noyau, cet état pouvant être normal ou bien excité, suivant le nombre de quanta correspondants. Étant donné l’ordre de grandeur des moments d’inertie qu’on peut envisager, on pourrait rendre compte ainsi de différences énergétiques modérées, soit un petit nombre de fois 10 eKV.
8. — Variation d’énergie interne dans les transformations nucléaires.
Pour un atome simple au point de vue isotopique le poids atomique est voisin d’un nombre entier P ; le noyau de cet atome contient donc P protons. Le nombre d’électrons étant également P pour l’atome neutre, N de ces électrons sont extranucléaires et P − N intranucléaires, si N est le nombre atomique. Les données très précises de l’analyse des masses, dues principalement à Aston, font connaître la masse d’ions de charge connue, d’où on déduit celle des atomes neutres en tenant compte de la masse de l’électron, la base adoptée étant . Pour calculer la masse du noyau, il conviendrait de retrancher celle de tous les électrons extranucléaires. Le poids atomique de l’électron au repos est environ 0,00055.
Aston a mesuré pour de nombreux éléments le « coefficient de condensation » (packing fraction) défini comme excès de masse atomique par proton sur le nombre entier voisin. Ce coefficient ω est maximum pour l’atome d’hydrogène, pour lequel il atteint 77,8 × 10-4. La courbe qui représente ω en fonction de P présente une allure assez régulière ; ω reste > 0 pour P < 16, prend ensuite des valeurs négatives et passe par un minimum vers P = 60, puis augmente, s’annule vers P = 200 et continue à augmenter au delà, selon une allure qui paraît linéaire. L’ordre de grandeur de ω étant 10-4, on voit que l’incertitude introduite dans le calcul de la masse des noyaux par la soustraction des masses des électrons extranucléaires pourrait ne pas être négligeable, s’il y avait un doute sur la masse à attribuer aux électrons, selon la vitesse dont ils pourraient être animés.
L’effet de condensation est relié à la perte d’énergie interne par la relation d’Einstein . Cette perte est particulièrement sensible dans le cas de l’atome d’hélium, considéré comme formé de 4 atomes d’hydrogène. Les masses atomiques rapportées à étant H = 1,00778 et He = 4,00216, la perte de masse par atome gramme d’hélium est 4 × 1,00778 − 4,00216 = 0,029 gr. En divisant cette quantité par le nombre d’Avogadro, on trouve pour la perte de masse par atome d’hélium 4,8 × 10-26 gr. et pour la perte d’énergie correspondante 4,3 × 10-5 ergs, soit 27 × 106 électron-volts. Les deux électrons extranucléaires de l’atome He n’ayant pas changé de masse, la perte d’énergie ci-dessus calculée porte sur la formation du noyau d’hélium ou « helion » à partir des 4 protons et 2 électrons constituants. Ainsi l’énergie de cohésion du noyau d’hélium est considérable, et il doit en être de même de sa stabilité.
Dans tous les atomes autres que l’hydrogène, la masse du proton est, comme dans l’hélium, en moyenne beaucoup plus voisine de 1 que celle du proton libre. Par conséquent, pour tout atome, la construction à partir de protons et d’électrons entraîne une perte d’énergie considérable. Si, d’autre part, on envisage la formation d’atomes d’hélium comme première étape et que l’on forme des atomes suivants à l’aide d’atomes d’hélium, en aussi grand nombre que possible, avec addition de quelques protons et électrons, l’énergie mise en jeu dans ce deuxième processus est beaucoup moins grande que dans le premier. Ces considérations permettent d’entrevoir pourquoi, dans les transformations radioactives, on observe l’émission de noyaux d’hélium et non celle de protons.
On admet fréquemment que les éléments se rangent par leurs poids atomiques dans 4 séries, pour lesquelles P est respectivement du type 4n, 4n + 1, 4n + 2 et 4n + 3, n étant le nombre des particules α constituantes. Le nombre de protons non engagés dans les noyaux d’hélium, est alors, au plus, égal à 3, et parmi les électrons nucléaires il y en a 2n faisant partie des noyaux d’hélium. Pour un tel aggrégat, le volume pourrait être peu différent de la somme des volumes des éléments, auquel cas le rayon du noyau serait approximativement proportionnel à . L’énergie de cohésion, calculée à partir des éléments de structure ainsi choisis, augmente avec n jusque vers n = 30, passe par un maximum et décroît à nouveau pour les valeurs de n plus élevées.
La relation entre la stabilité du noyau et le coefficient de condensation ou l’énergie de cohésion n’apparaît pas encore clairement. Pour les éléments non radioactifs on manque de base pour définir le degré de stabilité. Pour un radioélément, la stabilité est définie par la radioactive λ qui figure dans la loi exponentielle de transformation. La variation de λ avec P offre une allure complexe qui n’est nullement conforme à celle de la variation linéaire présumée de ω avec P dans la même région. Cependant, sans avoir jusqu’ici des déterminations directes de ω du plomb à l’uranium, on peut estimer qu’il n’y a pas de contradiction entre les valeurs de ω qui conviennent à Pb et à U d’après la courbe d’Aston et celles qu’on déduit du dégagement d’énergie dans les transformations successives depuis Ul à Pb206. Cette série de transformation comprend, par atome transformé, l’émission successive de 8 particules α et de 6 électrons nucléaires ; à la perte de masse calculée comme pour des particules au repos, égale à 32,012 unités de masse atomique, vient donc s’ajouter celle qui correspond à l’énergie des rayons émis et que l’on évalue, soit d’après la mesure de leurs vitesses, soit par celle de l’effet calorifique dû à leur absorption. La perte de masse supplémentaire ainsi évaluée est environ 0,05 unités de masse atomique, d’où un total de 32,06 unités. La différence entre les écarts à partir d’un nombre entier pour Ul et Pb206 devrait donc être environ 0,06, ce qui paraît conforme à la courbe d’Aston extrapolée.
Quand on envisage une transformation nucléaire provoquée, telles qu’il peut s’en produire par le choc de rayons α sur des atomes
légers, il est devenu usuel d’établir le bilan énergétique de
la transformation, en vue d’en contrôler la probabilité. Dans les
considérations de ce genre, il est nécessaire de faire intervenir les
variations d’énergie interne, qui correspondent à l’effet de condensation.
9. — Théorie de désintégration radioactive de Gamow.
La force de répulsion qui existe entre un noyau d’atome et une particule α placée à l’extérieur de celui-ci, à une distance r de son centre, est conforme à la loi de Coulomb tant que r reste supérieur à une limite r0 qu’on peut considérer comme le rayon du noyau. Jusqu’à cette limite l’énergie potentielle U de la particule dans le champ du noyau varie en raison inverse de r. Quand r < r0, les forces attractives commencent à agir ; U subit une diminution rapide et prend une valeur minimum U0 dans la région centrale du noyau (fig. 11), où une particule α peut séjourner. Le maximum Um de U, situé dans la zone limite du noyau, constitue une « barrière de potentiel » qui s’oppose à la pénétration de l’extérieur vers l’intérieur et inversement, pour toute particule dont l’énergie E est inférieure à Um. Au point de vue de la mécanique classique une telle pénétration est impossible, — mais au point de vue de la mécanique ondulatoire, il existe toujours, pour le passage considéré, une certaine probabilité qui augmente avec E.
Par conséquent, la constante radioactive λ qui mesure pour la particule α la probabilité de sortie du noyau, doit être une fonction croissante de E.
Gamow a calculé cette fonction en adoptant une forme simple pour la fonction U dont la valeur dans les limites du noyau n’est pas connue. Il a obtenu ainsi une formule qui donne λ en fonction de la vitesse v que possède la particule α à la sortie du noyau, ainsi que du nombre atomique N de ce noyau et du rayon r0 du noyau transformé.
Cette formule correspond à la relation expérimentale trouvée par Geiger et Nuttall entre la constante λ et le parcours R des

rayons α, mais elle introduit aussi les paramètres supplémentaires
N et r0. À l’aide des valeurs expérimentales de λ, v et N, on peut donc calculer le rayon nucléaire r0 pour les radioéléments
qui émettent des rayons α. Les valeurs ainsi trouvées, peu différentes entre elles, sont de l’ordre de 8 × 10-13 cm. Le rayon r0 croît avec la masse du noyau.
Pour les éléments des familles de l’uranium et du thorium, le
nombre P de protons constituants est respectivement du type
4n + 2 et 4n. Pour la famille de l’actinium, le type n’est pas connu avec certitude, mais il parait probable que pour le plomb d’actinium P = 207, et que, par conséquent, dans cette famille P = 4n + 3. Il en résulte, qu’il n’y a pas de superposition entre les valeurs de P relatives aux radioéléments qui se transforment avec émission de rayons α, à la seule exception des corps C qui subissent une transformation à bifurcation, et qui, pour cette raison, ont la même valeur de P que les corps C′. On peut donc représenter λ en fonction de v, N et r0 doit, en réalité, se réduire à une relation entre λ et P seulement. Cette relation mise sous forme de graphique a une allure complexe, d’apparence périodique, avec des analogies dans la position que les radioéléments d’une même famille occupent sur le graphique.
10. — Les rayons H. La transformation artificielle des éléments légers par le choc des rayons α.
Parmi les noyaux légers projetés par le choc de rayons α, les protons ont une importance particulière, car ils peuvent franchir dans l’air des distances plus grandes que celles des rayons α générateurs. D’après les lois du choc élastique, la vitesse communiquée à un proton, dans un choc central, par un rayon α de vitesse v0 et d’énergie w0 avant le choc, est u = 1,6 v0 correspondant à l’énergie 0,64 w0. À la vitesse u correspond, suivant la théorie du passage des particules chargées par la matière, un parcours R, égal à environ 4 R0, si R0 est le parcours d’un rayon α de vitesse v0. Le parcours des rayons H varie comme celui des rayons α, proportionnellement au cube de la vitesse, tant que R est supérieur à une valeur limite, de l’ordre de 2 centimètres. Les rayons H produits par le choc élastique, dits « rayons H naturels » ont un parcours maximum dans l’air qui est environ 28 centimètres ou 16 centimètres, selon qu’ils sont produits par les rayons α de RaC′ ou par ceux de Po.
Les méthodes d’étude des rayons H sont les mêmes que pour les
rayons α : méthode des scintillations, observation dans la chambre
à détente, mesure de l’ionisation et numération par effet ionisant,
mesure de la déviation dans un champ magnétique. Conformément
aux lois du choc élastique, l’émission de rayons H naturels
a lieu uniquement vers l’avant par rapport à celle des rayons α. Quand un rayon H est projeté dans une direction faisant un angle θ avec celle du rayon α générateur, son parcours est
, quantité qui s’annule pour . Pour que R′ dépasse le parcours du rayon α générateur, il est nécessaire que θ soit inférieur à une certaine limite voisine de 50°. Les rayons qui remplissent cette condition sont ceux qu’on a le plus étudiés, car ce sont ceux qu’on observe au delà du parcours des rayons α générateurs. Ils sont émis dans des chocs exceptionnels très peu fréquents, dont la proportion, par rayon α, a été calculée, en admettant que l’action répulsive du rayon α sur le proton s’exerce suivant la loi de Coulomb. Eu égard à l’effet de dispersion anomale, signalé plus haut, il y a désaccord sur ce point entre la théorie et l’expérience, l’écart augmentant avec la vitesse des rayons α générateurs, c’est-à-dire avec la réduction de la distance entre le rayon α et le proton, au moment du choc. Par exemple, en utilisant des rayons α de 8 centimètres de parcours, Chadwick et Bieler ont obtenu, dans la direction θ = 30°, environ 100 fois plus de rayons H que le nombre prévu, l’ordre de grandeur du nombre observé avec le dispositif expérimental considéré étant 4 × 10-3 rayons H par rayon α.

Les rayons H naturels sont produits soit dans l’hydrogène gazeux, soit dans un corps hydrogéné tel que la paraffine. Ils forment un faisceau hétérogène, même si les rayons α générateurs sont de même vitesse, car la vitesse d’un rayon H dépend de l’angle sous lequel il est émis. L’hétérogénéité est, en général, encore accrue du fait que les rayons α générateurs éprouvent un ralentissement dans la matière hydrogénée qu’ils traversent, et que les rayons H sont produits dans cette matière à diverses profondeurs de pénétration des rayons α. Un dispositif d’observation des rayons H naturels est représenté dans la fig. 12.
La projection de protons de grande vitesse peut avoir lieu non seulement quand les rayons α subissent des chocs exceptionnels dans une matière hydrogénée, mais aussi quand ces chocs ont lieu contre certains atomes légers tels que l’azote. Les protons, en ce cas, sont extraits des atomes d’azote, ce qui implique une transmutation atomique de ces derniers. Ce phénomène fondamental, découvert par Rutherford, est désigné comme « désintégration artificielle » ou « transmutation artificielle ». Pour l’observer, on peut employer un dispositif semblable à celui de la fig. 12. Les protons de désintégration peuvent avoir des vitesses et des parcours très supérieurs à ceux des rayons H naturels ; il en est ainsi, par exemple, dans le cas de l’azote, et c’est ce qui a permis de faire, dès le début, une distinction nette entre la désintégration et des effets parasites pouvant provenir de la présence d’hydrogène occlus dans la source ou dans les écrans.
Les observations les plus précises concernent les protons de désintégration de parcours supérieur à celui des rayons α générateurs ; cependant l’observation de parcours inférieurs à cette limite a été rendue possible par l’emploi de la « méthode rétrograde » qui consiste à envoyer les rayons α sur un radiateur et à observer les protons issus de celui-ci, dans une direction faisant un angle obtus avec celle des rayons α incidents (Pettersson).
La possibilité de transmutation avec émission de protons a été établie pour la plupart des éléments légers, jusqu’au potassium inclusivement. Pour Li, Be, C et O l’accord d’opinion n’est pas réalisé, et de même pour les éléments au delà du potassium. Les protons sont émis aussi bien vers l’avant que vers l’arrière, par rapport à la direction des rayons α incidents, la vitesse vers l’avant étant supérieure à celle vers l’arrière, conformément au principe de conservation de la quantité de mouvement. Mais le choc n’étant pas élastique, la vitesse comporte une composante sans direction privilégiée. Voici les valeurs des parcours vers l’avant et vers l’arrière pour quelques éléments, les rayons α utilisés ayant un parcours de 7 centimètres.
| B | Az | F | Na | Al | P | |
| Vers l’avant, cm. | 58 | 40 | 65 | 58 | 90 | 65 |
| Vers l’arrière, cm. | 38 | 18 | 48 | 36 | 67 | 43 |
D’après le calcul, un proton de parcours supérieur à 56 centimètres doit avoir une énergie supérieure à celle d’un rayon α dont le parcours est 7 centimètres. Il en est certainement ainsi pour le proton de désintégration émis vers l’avant par l’aluminium. Par conséquent, l’énergie interne du noyau intervient nécessairement dans la transmutation. Pour le proton de 90 centimètres de parcours, l’énergie est égaie à 1,4 fois celle du rayon α de RaC′ qui lui a donné naissance. Au lieu d’un dégagement d’énergie, la désintégration peut être accompagnée d’une absorption d’énergie, comme dans le cas de l’azote.
Le rendement de la désintégration est de l’ordre de 10 à 20 atomes transformés pour 106 rayons α de RaC′ ou de ThC′.
Les expériences faites par la méthode de détente de Wilson pour observer les fourches dues au choc de rayons α contre des noyaux légers, ont permis de mettre en évidence quelques cas de transmutation. Blacquett a observé 8 fourches, ne satisfaisant pas aux lois de choc élastique et présentant, après le choc, deux trajectoires, dont l’une fine et allongée, correspond au proton de transmutation, tandis que l’autre, courte et plus épaisse, correspond à un noyau d’azote qui aurait incorporé la particule α incidente. Il y a là un exemple de « transmutation avec capture » donnant lieu à la production d’un isotope d’oxygène de masse 17. Les quantités de mouvement des deux particules après choc sont calculées, par rapport à celle du rayon α incident, d’après les angles que forment, avec la direction de celui-ci, les bras de la fourche.
Si une transmutation avec capture est toujours accompagnée d’une même variation d’énergie Q, on peut calculer les quantités de mouvement (dont on admet la conservation) pour chaque direction d’émission du proton par rapport au rayon α incident. Les relations obtenues paraissent applicables à la transmutation de l’azote, tandis que dans d’autres cas, les conditions paraissent plus complexes. Au point de vue théorique on peut envisager les types d’interaction suivants, pour le choc non élastique d’un rayon α et d’un noyau :
1° Excitation du noyau, sans transmutation, avec perte d’énergie pour le rayon α et avec émission ultérieure de rayons γ.
2° Transmutation avec émission d’un proton et avec capture de la particule α.
3° Transmutation avec émission d’un proton, sans capture de la particule α, celle-ci étant renvoyée avec une vitesse réduite.
Ces problèmes ont été examinés au point de vue de la mécanique ondulatoire. La probabilité de l’excitation est d’autant plus petite que le niveau excité est plus élevé et que le nombre atomique est plus grand. La particule excitée serait un proton ou une particule α. Si le niveau excité est suffisamment élevé, la particule pourra quitter le noyau en traversant la barrière de potentiel, sans que la particule α incidente soit captée ; la probabilité de ce phénomène parait faible, surtout pour ce qui concerne l’émission d’une particule α intranucléaire. S’il s’agit de protons, les vitesses d’émission formeraient un spectre continu, en relation avec la perte de vitesse du rayon α incident qui prend toute valeur entre 0 et la vitesse initiale. La transmutation avec capture de la particule α sur un niveau déterminé, conduirait, au contraire, à l’émission de groupes homogènes de protons (spectre de raies).
La probabilité de transmutation avec capture est particulièrement élevée si l’énergie du rayon α incident est voisine de celle d’un niveau intranucléaire. Cet « effet de résonance » laisse prévoir l’émission de groupes de protons pour des vitesses de rayons α comprises entre certaines limites.
Admettons que la quantité Q d’énergie libérée est fixe pour une transmutation nucléaire avec capture, et que le principe de conservation des quantités de mouvement s’applique. Connaissant l’énergie du rayon α incident et celle du proton de désintégration dont on a mesuré le parcours, pour une direction d’émission déterminée, on peut calculer l’énergie de recul du noyau et la valeur de Q. Celle-ci est à comparer avec la perte de masse par effet de condensation, dans le cas où la valeur exacte de la masse serait connue aussi bien pour le noyau primitif que pour celui qu’on suppose formé lors du choc.
Les travaux de divers auteurs ont mis en évidence l’émission de groupes définis de protons de désintégration[4] par certains éléments.
Les rayons α utilisés étaient ceux de RaC′, de ThC′ ou du polonium. Pour l’azote, un seul groupe de protons a été signalé ; la transformation a lieu probablement avec capture. Elle est accompagnée d’une absorption d’énergie ; on trouve environ Q = −1,3 × 106 électron-volts.
Le bore émet trois groupes de protons dont deux sont attribués à une transmutation avec capture et le troisième pourrait correspondre à une transmutation sans capture (valeurs de Q en électron-volts 4,7 × 106, 0,6 × 106 et −1,1 × 106).
L’aluminium émettrait aussi 2 ou 3 groupes de protons (valeurs
de Q −3 × 106 et 0,25 × 106 électron-volts), et il semble qu’on ait observé aussi un effet de résonnance.
11. — Excitation de rayons très pénétrants dans les atomes légers sous le choc de rayons α. Projection de noyaux légers. Hypothèse du neutron.
En soumettant diverses substances au bombardement par les rayons α du polonium, Bothe et Becker ont observé que certains atomes légers émettent, dans ces conditions, un rayonnement de faible intensité, plus pénétrant que les rayons γ les plus durs observés chez les radioéléments. Ce phénomène a été interprété comme une émission de rayons γ par les noyaux, à la suite d’une excitation de ceux-ci, avec ou sans transmutation[5]. Tous les éléments depuis Li jusqu’à Al donnent cet effet, et c’est pour Be que le phénomène a la plus grande intensité ; viennent ensuite le bore et le lithium. Les observations de Bothe et Becker étaient faites à l’aide d’un compteur électrique. Le rendement en quanta paraissait du même ordre que celui de la désintégration.
Irène Curie et F. Joliot ont repris ces expériences, en mesurant, par un dispositif sensible, l’ionisation produite par les rayons pénétrants de Be, de B et de Li, et en ayant recours à de fortes préparations de polonium, comme sources de rayons α (de l’ordre de 100 millicuries). L’absorption de moitié du rayonnement de Be dans le plomb correspond à une épaisseur d’environ 4 cm. 7, d’où pour un rayonnement γ, un quantum de l’ordre de 15 × 106 volts.
L’étude de l’absorption de ce rayonnement, désigné pour abréger par le symbole (Po + Be), dans diverses matières interposées entre la source et la chambre d’ionisation, en masses superficielles égales, a fait ressortir ce fait inattendu que le courant (de l’ordre de 10−5 E. S.), mesuré avec des écrans de C, Al ou Cu est à peu près le même, mais beaucoup plus petit que celui qu’on observe avec des écrans de paraffine ou cellophane. I. Curie et F. Joliot ont montré que les rayons (Po + Be) traversant les corps hydrogénés, projettent des protons de grande vitesse qui pénètrent dans la chambre d’ionisation au travers de la face d’entrée fermée par une feuille très mince d’aluminium, et qui ionisent l’air énergiquement. Le parcours de ces protons peut atteindre 70 centimètres[6].
L’effet de projection n’est pas limité aux noyaux d’hydrogène ; mais se produit aussi pour d’autres noyaux légers : He, Az, etc. Il est confirmé par des expériences faites avec une chambre à détente qui reçoit de l’extérieur les rayons excitateurs. Si celle-ci contient une plaque de paraffine, on voit des trajectoires de protons issus de la paraffine ; d’autres protons prennent naissance dans l’air de la chambre qui contient des molécules d’eau. Si la chambre contient de l’hélium, on obtient les trajectoires de noyaux He.
La méthode de détente permet aussi de reconnaître des trajectoires d’électrons dont les énergies, évaluées d’après la déviation dans un champ magnétique, sont de quelques millions d’électronvolts.
Les auteurs ont montré que l’interprétation de leurs expériences soulève des difficultés si on considère le phénomène comme un effet Compton produit par des rayons γ sur des noyaux d’atomes. Chadwick a admis que les rayons responsables de la projection sont des neutrons, particules de masse voisine de 1, formées par une association particulièrement intime d’un proton et d’un électron. La possibilité d’existence de tels rayons avait été, à plusieurs reprises, envisagée précédemment, mais les essais de leur recherche n’avaient abouti à aucun résultat concret. Chadwick a montré que la production d’un neutron dans le bombardement de Be par les rayons α de Po pouvait avoir lieu selon la relation : Be + α = neutron + C12 et qu’en tenant compte de l’énergie de cohésion, on obtient ainsi pour le neutron de masse 1 une énergie de l’ordre de celle du proton projeté.
Les expériences de M. de Broglie et de ses collaborateurs ainsi que celles de P. Auger et de Rasetti ont apporté de nouvelles contributions à l’appui du phénomène nouveau[7].
L’émission de neutrons sous le choc de rayons α a été établi, en outre de Be, pour B, Li, F et Al. Dans tous ces cas, on doit conclure à une transmutation des noyaux rencontrés, le mode de transmutation étant ici différent de celui qui consiste dans l’émission d’un proton.
En même temps se pose le problème relatif au rôle du neutron dans le noyau dont il provient. On doit peut-être considérer le neutron comme un élément de structure nucléaire à l’égal du proton ou de l’hélion. Certains auteurs supposent que les électrons nucléaires sont tous engagés soit dans des hélions, soit dans des neutrons. On envisage aussi l’existence de demi hélions, résultant de l’addition d’un neutron et d’un proton (F. Perrin). Le nombre d’éléments de structure nucléaire à prendre en considération s’est donc accru du fait de la découverte des neutrons.
Il semble de plus qu’à côté d’électrons, à charge négative, on doive admettre l’existence de particules ayant une masse de même ordre avec une charge positive : « électrons positifs ». Ces particules découvertes au cours de recherches sur le rayonnement cosmique (Anderson, Blackett et Occhialini) apparaissent aussi quand les éléments lourds, par exemple le plomb, sont soumis à l’action des rayons γ durs tels que ceux de Thc″ (I. Curie et F. Joliot).
Les neutrons qui possèdent une énergie suffisante sont capables de produire la transmutation de noyaux qu’ils rencontrent. On voit l’exemple de tel processus dans des clichés obtenus par la méthode Wilson. La trajectoire du neutron n’est pas rendue visible, cette particule n’étant pas douée de pouvoir ionisant, mais du point de choc contre un noyau d’azote, on voit partir les trajectoires du rayon α et du noyau de bore qui sont les produits présumés de la réaction nucléaire : neutron + N14 = α + B11, inverse de celle par laquelle un rayon α produit un neutron par rencontre avec un noyau de bore.
12. — Transmutations par les protons et par les rayons cosmiques. Conclusions.
La découverte récente des transmutations produites par le choc des protons (Cockroft et Walton) a prouvé que là aussi il existe une certaine réciprocité. Un proton peut pénétrer dans un noyau au travers de la barrière de potentiel, même quand son énergie est modérée (100 eKV, par exemple) ; il produit une transmutation qui, dans le cas de Li, consiste dans l’émission de rayons α de grande vitesse, effet prévu par Gamow sur la base de considérations énergétiques.
Les rayons cosmiques sont également capables de produire des transmutations ainsi qu’il résulte de recherches récentes de plusieurs auteurs.
Les phénomènes de transmutation ainsi multipliés, sont un moyen puissant pour l’exploration de la structure nucléaire[8].
On peut estimer que le champ d’investigation ouvert à la physique nucléaire s’est considérablement élargi. Comprenant d’abord presque exclusivement l’étude du rayonnement des corps radioactifs, comme il a été exposé ci-dessus, il a pu bénéficier ensuite de nouveaux moyens d’action apportés par les protons en mouvement et par les rayons cosmiques. On peut espérer voir se poursuivre avec une rapidité accrue, le merveilleux développement de ce nouveau domaine.
IMPRIMERIE BARNÉOUD
— LAVAL (FRANCE) —
- ↑ S. Rosenblum, Actualités Scientif., Hermann, etc.
- ↑ Fournier et Guillot. Collection actualités, etc…
- ↑ Gamow, Constitution of Atomic Nuclei and Radioactivity, Oxford, 1931.
- ↑ Rutherford et Chadwick, Phil. Mag., 42 (1921), 809, Proc. Cam. Ph. Soc., 25 (1929), 186 ; Bothe et Franz, Zs. f. Phys., 49 (1928), 1 ; Pose, Zs. f. Phys., 64 (1929), 1 : 67 (1931), 194 ; Chadwick, Constable et Pollard, Proc. Roy. Soc., 130 (1931), 463 ; Chadwick et Constable, Proc. Roy. Soc., 135 (1932), 48 ; de Broglie et Leprince-Ringuet, C. R. 193 (1931), 132.
- ↑ Bothe et Becker, Zs. f. Ph., 46 (1930), 289 ; Naturw., 19 (1931), 753.
- ↑ Irène Curie et F. Joliot, C. R., 194 (1932), 278.
- ↑ Voir l’exposé d’ensemble par Irène Curie et F. Joliot dans « Actualités, etc. ».
- ↑ Voir l’exposé de Leprince-Ringuet : Actualités Scientifiques Hermann et Cie, n° 55.




![{\displaystyle W=m_{0}c^{2}\left[{\frac {1}{\sqrt {1-\beta ^{2}}}}-1\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/ae4ca20d8ab289ec94e5670575c029f479e0502e)












![{\displaystyle W=mc^{2}\left[{\frac {1}{\sqrt {1-\beta ^{2}}}}-1\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/797f60d151921becdde3ad088735321dd9e1bcb7)



















