Sur la preuve de la réalité de l’éther lumineux
Cette formule, dans laquelle on considére R et φ comme variables, représente une onde sphérique issue du point O, dont amplitude décroît (dans la région de espace φ > α) sur la surface même de l’onde suivant une loi exponentielle. Cette onde peut donc s’appeler légitimement onde sphérique inhomogène.
L’existence de ces ondes est facile à constater par le dispositif suivant : On porte sur l’hypoténuse d’un prisme à réflexion totale une goutte de solution de fluorescéine ; on fait tomber de la lumiére sur cette goutte qui devient fluorescente et l’on observe de près, les yeux accommodés sur l’infini, la surface du cône de la réflexion totale. Il apparaît alors que l’intensité lumineuse n’est pas nulle a l’extérieur du cône, mais au contraire perceptible à l’œil. Cela tient à ce que les centres lumineux, situés à proximité de la surface du verre, envoient de la lumiére dans la région de l’espace extérieure au cône et ils en envoient d’aulant plus qu’ils sont plus près de la surface.
Il est à remarquer que ces ondes inhomogènes, tout en trahissant la présence d’un objet lumineux, même si cet objet est regardé du second milieu sous un angle supérieur a celui de la réflexion totale, ne peuvent former qu’une image dont l’épaisseur est nulle dans la direction de la normale a la surface de séparation.
Le problème traité ici par des moyens élémentaires peut être posé dans le cas où la source lumineuse est un double pôle de Hertz. Il s’agit alors de déterminer les lois de réflexion et de réfraction des ondes qui sortent du double pôle ; la solution peut s’obtenir en utilisant, sous une forme précise, le principe du retour inverse des rayons lumineux. Nous nous en occuperons, ainsi que de quelques autres phénoménes optiques s’y rattachant, dans un prochain travail plus détaillé.
Dans les Comptes rendus du 27 octobre dernier (p. 708 de ce Volume), j’ai montré qu’un interférographe dont le circuit optique entoure une certaine aire, et qui tourne dans le plan de ce circuit, enregistre son mouvement d’ensemble par rapport à l’éther du vide.
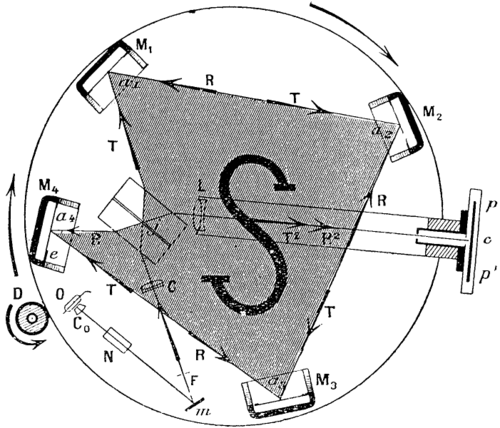
1. L’interférographe, déjà décrit succinctement, est représenté en plan sur la figure : un plateau tournante horizontal (50cm de diamètre) porte, solidement vissées (les vis de réglage bloquées par des contre-vis), toutes les pièces optiques et aussi la source lumineuse O, petite lampe électrique à filament métallique horizontal. L’objectif de microscope C0 projette l’image de ce filament, à travers le nicol N, sur la fente horizontale F dans le plan focal de l’objectif collimateur C ; m est un miroir de renvoi. Le faisceau parallèle polarisé, à vibration de Fresnel verticale, se divise sur le séparateur à lame d’air , comme dans l’interféromètre habituel de mes recherches (Comptes rendus, t. 150, 1910, p. 1676), que j’ai appliqué à l’étude optique du mouvement de la Terre (Congrès de Bruxelles, sept. 1910, t. I, p. 207 ; Comptes rendus, t. 152, 1911, p. 310 ; Le Radium, 1911, p. I) : le faisceau T que transmet la lame d’air se réfléchit successivement sur quatre miroirs M et parcourt le circuit fermé d’aire S. Le faisceau R que réfléchit la même lame d’air parcourt le même circuit en sens inverse. Au retour en , le faisceau T, transmis de nouveau, et le faisceau R, réfléchi de nouveau, se superposent dans le même sens, suivant T² et R², et interfèrent au foyer principal de la lunette L sur la plaque photographique pp’à grain fin.
2. Mode opératoire. Je rappelle que la superposition parfaite des deux faisceaux inverses T et R se caractérise par l’extinction générale du champ de la lunette pour la radiation utilisée qui est ici voisine de la radiation indigo de l’arc au mercure. A partir de là, une légère rotation ε du séparateur autour d’un axe vertical, dans le sens dextrorsum (bascule D), ou sinistrorsum (bascule S), rétrécit le champ sombre en une frange verticale centrale que bordent des franges latérales parallèles.
Les franges réglées, la plaque pp’calée dans son châssis et découverte à la lumière rouge, je lance progressivement un moteur électrique dont l’axe vertical porte un disque horizontal D, entouré d’un cuir et roulant par ce cuir sur la jante épaisse du plateau. La fréquence N désirée atteinte, je fais la pose photographique en établissant le courant électrique de la petite lampe O, par un contact glissant sur l’axe du plateau tournant.
3. Sens et grandeur de l’effet tourbillonnaire optique. — Dans l’hypothèse de l’éther de Fresnel, les ondes lumineuses T et R se propagent dans l’éther du vide avec une vitesse V0 indépendante du mouvement d’ensemble de l’interférographe ; la phase des ondes T de sens de propagation dextrorsum (voir la figure) est altérée le long du circuit fermé, comme si l’éther lumineux était animé d’un tourbillon sinistrorsum, quand le circuit tourne dans le sens d et la valeur 4πNS de ce tourbillon, ou circulation relative C de l’éther dans le circuit optique donne, par la formule , le retard x de phase des ondes T et l’avance égale des ondes R de propagation inverse ; les franges doivent se déplacer de 2x rangs. Le sens absolu de ce déplacement y des franges doit être pp’, c’est-à-dire d, comme la rotation de l’interférographe (effet de sens positif), si la bascule du réglage est de sens D ; le
déplacement z, égal à 2y ou 4x, mesuré en passant d’une photographie s à une photographie d, doit être alors de sens d. Si la bascule du réglage est de sens S, les déplacements y et z doivent changer de sens.
Sur de nombreuses épreuves, j’ai constamment observé le sens ainsi prévu. Le fait que l’effet z se renverse quand je fais tourner le séparateur d’une fraction de degré seulement, pour renverser le sens de bascule de réglage, caractérise l’effet comme différence de phase liée au mouvement de l’interférographe, et permet de le distinguer de l’effet de déformation des pièces optiques.
Voici des exemples de mesures de z comparées avec les valeurs calculées par la formule ; j’ai déterminé la longueur d’onde λ proportionnellement à l’interfrange obtenue avec la petite lampe O et comparée à l’interfrange peu différente obtenue avec la radiation 436mμ d’un arc au mercure. Les mesures sont faites par l’une des deux méthodes indiquées dans ma Note du 27 octobre dernier. La frange centrale c, claire sur le négatif étudié, et les franges latérales f sombres, ne sont bordées que de pénombres assez étroites, favorables à la précision des pointés que j’effectue à un faible grossissement, en encadrant la frange pointée entre les deux fils parallèles d’un micromètre oculaire.
| Bascule. | N. | z par c | z par f. | z calc. | |
| Méthode 1 (S=863cm²).... | S | 0,86 | -0,026 | » | -0,029 |
| D | 1,88 | +0,070 | » | +0,065 | |
| Méthode 2 (S=866cm²).... | S | 2,2 | -0,072 | -0,078 | -0,075 |
| S | 2,35 | -0,077 | -0,080 | -0,079 |
L’interférographe enregistre et mesure, par z, l’effet tourbillonnaire, au premier ordre, de son mouvement d’ensemble, sans emprunter aucun repère extérieur.
Le résultat des mesures montre que, dans l’espace ambiant, la lumière propage avec une vitesse V0, indépendante du mouvement d’ensemble de la source lumineuse O et du système optique. Cette propriété de l’espace caractérise expérimentalement l’éther lumineux. L’interférographe mesure, par , la circulation relative de l’éther lumineux dans le circuit fermé .







