Théorie de la musique (Danhauser, 1889)/III/6
6e Leçon.
DE L’ENCHAÎNEMENT DES GAMMES.
(ORDRE DES BÉMOLS.)
123. Nous avons vu, dans la 4e leçon, qu’en transformant le tétracorde supérieur de la gamme d’Ut en tétracorde inférieur d’une nouvelle gamme, nous trouvions une tonalité nouvelle, contenant un dièse ; puis, qu’en procédant de même, prenant tour à tour chaque nouvelle gamme comme point de départ, nous parcourions toutes les tonalités renfermant des dièses.
En faisant l’opération inverse, c’est à dire, en transformant le tétracorde inférieur de la gamme d’ut, en tétracorde supérieur d’une nouvelle gamme, nous trouverons encore une tonalité nouvelle, contenant un bémol ; puis, procédant de même, en prenant tour à tour chaque nouvelle gamme comme point de départ, nous parcourrons successivement toutes les tonalités renfermant des bémols.
124. Transformons le tétracorde inférieur de la gamme d’ut, en tétracorde supérieur d’une autre gamme.
Ce tétracorde, nous le savons, est formé des quatre notes :
| tétracorde inférieur de la gamme d’ut, transformé en tétracorde supérieur d’une nouvelle gamme. | |
| Ex. |  |
Pour compléter cette nouvelle gamme, il faut ajouter un tétracorde nouveau, formé des quatre degrés descendants qui précédent immédiatement le tétracorde supérieur, soit, les quatre notes :

125. Ce nouveau tétracorde ne peut cependant être admis, puisqu’il n’est pas conforme au second, c’est à dire que les notes qui le composent, au lieu de se succéder dans cet ordre.
se succèdent ainsi :
Le Si est trop éloigné du La, note inférieure, puisque ces deux notes sont séparées par un ton, et non par un demi-ton.
Le même Si est trop rapproché de l’Ut, puisque les deux tétracordes doivent être séparés par une seconde majeure, et qu’ils le sont par une seconde mineure.
Enfin, les deux notes extrêmes du tétracorde « Fa — Si » au lieu d’être à distance de Quarte juste, sont à distance de Quarte augmentée.
Or, le Si étant trop éloigné de la note inférieure et trop rapproché de la note supérieur, il faut l’abaisser d’un demi-ton chromatique, par le bémol, et lui donner ainsi la position qu’il doit occuper régulièrement dans le tétracorde, pour former une gamme régulière.
| Ex. | 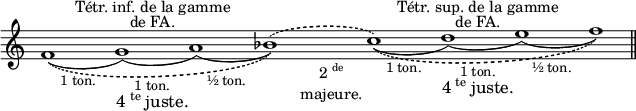 |
| gamme de fa. |
126. Le son nouveau trouvé pour former cette gamme est le Si ![]() , sous-dominante
de cette nouvelle gamme.
, sous-dominante
de cette nouvelle gamme.
Fa, premier degré, est la Tonique.
Ut, cinquième degré, est la Dominante.
Les notes tonales sont :
Fa, 1er degré ; Si ![]() , 4e degré ; et Ut, 5e degré.
, 4e degré ; et Ut, 5e degré.
127. Le même fait se reproduira toujours, quand nous transformerons le tétracorde inférieur d’une gamme en tétracorde supérieur d’une autre gamme. Chaque gamme nouvelle nous présentera un son nouveau, et ce nouveau son sera le quatrième degré de la gamme nouvelle, abaissé d’un demi-ton chromatique par le bémol.
128. Examinez attentivement le tableau suivant :
de l’enchaînement des gammes
par la transformation du
tétracorde inférieur en
tétracorde supérieur
d’une autre
gamme.
(ordre des bémols)

On voit par ce tableau :
1o Que chaque gamme a son tétracorde supérieur commun avec la gamme qui la précède, (qui a un bémol de moins), et son tétracorde inférieur commun avec la gamme qui la suit, (qui a un bémol de plus.)
2o Que les gammes qui contiennent des notes bémolisées se succèdent par une progression descendante de Quinte en Quinte.[1]
3o Que chaque nouveau bémol se présente également dans l’ordre descendant de Quinte en Quinte.[1]
SUCCESSION DES BÉMOLS.
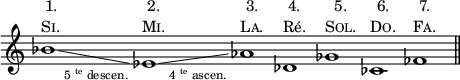
129. Remarquez que l’ordre des bémols est exactement inverse de l’ordre des dièses. (Comparez avec le tableau de la succession des dièses, 4e leçon. § 118).
| 7. | 6. | 5. | 4. | 3. | 2. | 1. | — ordre des bémols. | |
| FA, | UT, | SOL, | RÉ, | LA, | MI, | SI, | ||
| ordre des dièses — | 1. | 2. | 3. | 4. | 5. | 6. | 7. | |
Écrivez à la suite les unes des autres, et dans leur ordre successif, toutes les gammes contenant des notes bémolisées. Indiquez la tonique, la sous-dominante et la note sensible de chacune d’elles, ainsi que le nombre et le nom des bémols qui s’y trouvent.


