Traité de dynamique/1758/Partie 1/Chapitre 1

Jean le Rond d’Alembert

Traité de dynamique

David l'aîné, 1758 (p. 3-34).

PREMIERE PARTIE.

Loix générales du mouvement & de l’équilibre des Corps.

1.
On peut réduire tous les Principes de la Mécanique à trois, la force d’inertie, le mouvement composé, & l’équilibre. Au moins j’espere faire voir par ce Traité, que toute cette science peut être déduite de ces trois Principes. Je traiterai de chacun en particulier dans chacun des Chapitres suivans.

CHAPITRE PREMIER.

De la force d’inertie, & des propriétés du mouvement qui en résultent.

2.
J’apelle avec M. Newton force d’inertie, la propriété qu’ont les Corps de rester dans l’état où ils sont : c’est cette propriété qu’il faut démontrer ici. Or un Corps est nécessairement dans l’état de repos ou dans celui de mouvement ; il faut donc démontrer les deux Loix suivantes.

I. Loi.

3. Un Corps en repos y persistera, à moins qu’une cause étrangere ne l’en tire. Car un Corps ne peut se déterminer de lui-même au mouvement, puisqu’il n’y a pas de raison pour qu’il se meuve d’un côté plutôt que d’un autre.

Corollaire.

4. Delà il s’ensuit, que si un Corps reçoit du mouvement par quelque cause que ce puisse être, il ne pourra de lui-même accélérer ni retarder ce mouvement.

5. On appelle en général puissance ou cause motrice, tout ce qui oblige un Corps à se mouvoir.

ii. Loi.

6. Un Corps mis une fois en mouvement par une cause quelconque, doit y persister toujours uniformément & en ligne droite, tant qu’une nouvelle cause, différente de celle qui l’a mis en mouvement, n’agira pas sur lui ; c’est-à-dire, qu’à moins qu’une cause étrangere & différente de la cause motrice, n’agisse sur ce Corps, il se mouvra perpétuellement en ligne droite, & parcourra en tems égaux des espaces égaux.

Car, ou l’action Indivisible & instantanée de la cause motrice au commencement du Mouvement, suffit pour faire parcourir au Corps un certain espace, ou le Corps a besoin pour se mouvoir de l’action continuée de la cause motrice.

Dans le premier cas, il est visible que l’espace parcouru ne peut être qu’une ligne droite décrite uniformément par le Corps mû. Car (hyp.) passé le premier instant, l’action de la cause motrice n’existe plus, & le Mouvement néanmoins subsiste encore : il sera donc nécessairement uniforme, puisque (Art. 4) un Corps ne peut accélérer ni retarder son Mouvement de lui-même. De plus, il n’y a pas de raison pour que le Corps s’écarte à droite plutôt qu’à gauche. Donc dans ce premier cas où l’on suppose qu’il soit capable de se mouvoir de lui-même pendant un certain tems, indépendamment de la cause motrice, il se mouvra de lui-même pendant ce tems uniformément & en ligne droite.

Or un Corps qui peut se mouvoir de lui-même uniformément & en ligne droite pendant un certain tems, doit continuer perpétuellement à se mouvoir de la même manière, si rien ne l’en empêche. Car supposons le Corps partant de $A\,\!$, (Fig. 1^re) & capable de parcourir de lui-même uniformément la ligne $AB\,\!$; soient pris sur la ligne $AB\,\!$ deux points quelconques $C\,\!$, $D\,\!$, entre $A\,\!$ & $B\,\!$. Le Corps étant en $D\,\!$ est précisément dans le même état que lorsqu’il est en $C\,\!$, si ce n’est qu’il se trouve dans un autre lieu. Donc il doit arriver à ce Corps la même chose que quand il est en $C\,\!$. Or étant en $C\,\!$ il peut (hyp.) se mouvoir de lui-même uniformément jusqu’en $B\,\!$. Donc étant en $D\,\!$ il pourra se mouvoir de lui-même uniformément jusqu’au point $G\,\!$, tel que $DG=CB\,\!$, & ainsi de suite.

Fig. 1

Donc si l’action premiere & instantanée de la cause motrice est capable de mouvoir le Corps, il sera mû uniformément & en ligne droite, tant qu’une nouvelle cause ne l’en empêchera pas.

Dans le second cas, puisqu’on suppose qu’aucune cause étrangere & différente de la cause motrice n’agit sur le Corps, rien ne détermine donc la cause motrice à augmenter ni à diminuer ; d’où il s’ensuit que son action continuée sera uniforme & constante, & qu’ainsi pendant le tems qu’elle agira, le Corps se mouvra en ligne droite & uniformément. Or la même raison qui a fait agir la cause motrice constamment & uniformément pendant un certain tems, subsistant toujours tant que rien ne s’oppose à son action, il est clair que cette action doit demeurer continuellement la même, & produire constamment le même effet. Donc &c.

Donc en général un Corps mis en mouvement par quelque cause que ce soit, y persistera toujours uniformément & en ligne droite, tant qu’aucune cause nouvelle n’agira pas sur lui.

La ligne droite qu’un Corps décrit ou tend à décrire, est nommée sa direction.

REMARQUE PREMIERE.

7. Je me suis un peu étendu sur la preuve de la seconde Loi, parce qu’il y a eu & qu’il y a peut-être encore quelques Philosophes qui prétendent que le mouvement d’un Corps doit de lui-même se ralentir peu à peu, comme il semble que l’Expérience le prouve. Il faut convenir au reste que toutes les preuves qu’on a données jusqu’ici de la conservation du mouvement, n’ont point le degré d’évidence nécessaire pour convaincre l’esprit ; elles sont presque toutes fondées, ou sur une force qu’on imagine dans la matiere, par laquelle elle résiste à tout changement d’état, ou sur l’indifférence de la matiere au mouvement comme au repos. Le premier de ces deux, Principes, outre qu’il suppose dans la matiere un Etre dont on n’a point d’idée nette, ne peut suffire pour prouver la Loi dont il est question. Car quand un Corps se meut, même uniformément, le mouvement qu’il a dans un instant quelconque, est distingué & comme isolé du mouvement qu’il a eu ou qu’il aura dans les instans précédens ou suivans. Le Corps est donc en quelque maniere à chaque instant dans un nouvel état, dans un état qui n’a rien de commun avec le précédent ; il ne fait, pour ainsi dire, continuellement que commencer à se mouvoir, & on pourrait croire qu’il tendrait sans cesse à retomber dans le repos, si la même cause qui l’en a tiré d’abord, ne continuoit en quelque sorte à l’en tirer toujours.

A l’égard de l’indifférence de la matiere au Mouvement ou au repos, tout ce que ce Principe présente, ce me semble, de bien distinct : à l’esprit, c’est qu’il n’est pas essentiel à la matiere de se mouvoir toujours, ni d’être toujours en repos ; mais s’ensuit-il clairement de là qu’un Corps en Mouvement ne puisse tendre continuellement au repos ? Ce n’est pas que le repos lui soit plus essentiel que le Mouvement ; mais on pourroit penser qu’il ne faut autre chose à un Corps pour être en repos, que d’être un Corps, au lieu que pour le Mouvement il a peut-être besoin de quelque chose de plus, qui doit être, pour ainsi dire, continuellement reproduit en lui ; à peu près comme nous l’éprouvons dans le mouvement de notre corps, qui pour se mouvoir a besoin d’un effort continuel, lequel se consume & renaît à chaque instant. Nous ne prétendons pas donner pour juste le parallele des corps animés aux corps inanimés ; mais ce parallele peut au moins faire croire confusément, quoique sans raison, qu’il y a quelque chose dans un corps en mouvement qui n’est pas dans un corps en repos, & suffit par conséquent pour rendre insuffisante la preuve que nous examinons ici.

La démonstration donnée ci-dessus de la conservation du Mouvement, a cela de particulier, qu’elle a lieu également, soit que la cause motrice doive toujours être appliquée au Corps, ou non. Ce n’est pas que je croye l’action continuée de cette cause, nécessaire pour mouvoir le Corps ; car si l’action instantanée ne suffisoit pas, quel seroit alors l’effet de cette action ? Et si l’action instantanée n’avoit point d’effet, comment l’action continuée en auroit-elle ? Mais comme on doit employer à la solution d’une question le moins de Principes qu’il est possible, j’ai cru devoir me borner à démontrer que la continuation du Mouvement a lieu également dans les deux hypotheses ; il est vrai que notre démonstration suppose l’existence du Mouvement, & à plus forte raison sa pos sibilité ; mais nier que le Mouvement existe, c’est se refuser à un fait que personne ne révoque en doute.

REMARQUE SECONDE.

8. L’expérience est d’accord avec le raisonnement pour prouver le principe de la force d’inertie : 1º. Nous voyons que les corps qui nous environnent restent en repos, tant que rien ne les en tire ; & s’il arrive quelquefois qu’ils paroissent se mouvoir sans que nous en voyons la cause, nous avons lieu de juger par l’analogie, par l’uniformité des loix de la nature, & par l’incapacité de la matiere à se mouvoir d’elle-même, que cette cause n’en est pas moins réelle pour nous être cachée. 2º. Quoiqu’il n’y ait point de corps qui conserve éternellement son mouvement, puisqu’il y a toujours des causes qui le ralentissent peu-à-peu, comme le frottement & la résistance de l’air, cependant nous voyons qu’un corps en mouvement y persiste d’autant plus long-tems que les causes qui retardent ce mouvement sont moindres ; d’où nous pouvons conclure que le mouvement ne finiroit point, si les causes retardatrices étoient nulles^[1].

Du Mouvement uniforme.

9. Nous venons de voir qu’un Corps se meut unifor mément & en ligne droite, quand aucune cause étrangere n’agit sur lui. D’où il s’ensuit que le même Corps peut encore se mouvoir uniformément, lorsque deux causes étrangeres agissent en même-tems & également, l’une pour accélérer, l’autre pour retarder son Mouvement. (C’est ainsi, pour le dire en passant, que les Corps qui tombent parviennent à se mouvoir uniformément, lorsque la résistance du Fluide ou ils se meuvent tend à diminuer leur mouvement, autant que leur pesanteur tend à l’augmenter). Dans tout autre cas, le Mouvement est nécessairement accéléré ou retardé.

10. Si deux parties quelconques $AB\,\!$, $AC\,\!$ (Fig. 2) d’une ligne indéfinie $AO\,\!$ représentent deux portions du tems écoulé depuis le commencement du Mouvement, & les lignes $BD\,\!$, $CE\,\!$, les espaces parcourus durant ces tems par un Corps dont le Mouvement est uniforme, les points $D\,\!$, $E\,\!$, seront à une ligne droite $ADE\,\!$.

Fig. 2

Car, puisqu’un Corps qui se meut uniformément parcourt des espaces égaux en tems égaux, les points $D\,\!$, $E\,\!$, doivent être à une ligne telle, que si on prend $AB\,\!$, $BC\,\!$ égales entr’elles & quelconques, on ait toujours $BD=FE\,\!$. Or cette propriété n’appartient qu’à la ligne droite. Donc &c.

Corollaire.

11. $BD:CE::AB:AC\,\!$. C’est-à-dire que dans le Mouvement uniforme, les espaces sont entr’eux comme les tems employés à les parcourir.

Remarque sur la mesure du tems.

12. Comme le rapport des parties du tems nous est inconnu en lui-même, l’unique moyen que nous puissions employer pour découvrir ce rapport, c’est d’en chercher quelqu’autre plus sensible & mieux connu, auquel nous puissions le comparer ; on aura donc trouvé la mesure du tems la plus simple, si on vient à bout de comparer de la maniere la plus simple qu’il soit possible, le rapport des parties du tems, avec celui de tous les rapports que l’on connoît le mieux. Delà il résulte que le Mouvement uniforme est la mesure du tems la plus simple. Car d’un côté, le rapport des parties d’une ligne droite est celui que nous saisissons le plus facilement ; & de l’autre, il n’y a point de rapports plus aisés à comparer entr’eux, que des rapports égaux. Or dans le Mouvement uniforme, le rapport des parties du tems est égal à celui des parties correspondantes de la ligne parcourue. Le Mouvement uniforme nous donne donc tout à la fois le moyen, & de comparer le rapport des parties du tems au rapport qui nous est le plus sensible, & de faire cette comparaison de la maniere la plus simple ; nous trouvons donc dans le Mouvement uniforme, la mesure la plus simple du tems.

Je dis outre cela, que la mesure du tems par le Mouvement uniforme, est, indépendamment de sa simplicité, celle dont il est le plus naturel de penser à se servir. En effet, comme il n’y a point de rapport que nous con noissions plus exactement que celui des parties de l’espace, & qu’en général un Mouvement quelconque dont la loi seroit donnée, nous conduiroit à découvrir le rapport des parties du tems, par l’analogie connue de ce rapport avec celui des parties de l’espace parcouru ; il est clair qu’un tel Mouvement seroit la mesure du tems la plus exacte, & par conséquent celle qu’on devroit mettre en usage préférablement à toute autre. Donc, s’il y a quelque espece particuliere du Mouvement, où l’analogie entre le rapport des parties du tems & celui des parties de l’espace parcouru, soit connue indépendamment de toute hypothese, & par la nature du Mouvement même, & que cette espece particuliere de Mouvement soit la seule à qui cette propriété appartienne, elle sera nécessairement la mesure du tems la plus naturelle. Or il n’y a que le Mouvement uniforme qui réunisse les deux conditions dont nous venons de parler. Car (art. 6) le Mouvement d’un Corps est uniforme par lui-même : il ne devient accéléré ou retardé qu’en vertu d’une cause étrangere, & alors il est susceptible d’une infinité de loix différentes de variation. La loi d’uniformité, c’est-à-dire l’égalité entre le rapport des tems & celui des espaces parcourus, est donc une propriété du Mouvement considéré en lui-même. Le Mouvement uniforme n’en est par-là que plus analogue à la durée, & par conséquent plus propre à en être la mesurre, puisque les parties de la durée se succedent aussi constamment & uniformément. Au contraire, toute loi d’accélération ou de diminution dans le Mouvement, est arbitraire, pour ainsi dire, & dépendante de circonstances extérieures. Le Mouvement non uniforme ne peut être par conséquent la mesure naturelle du tems ; car en premier lieu, il n’y auroit pas de raison pourquoi une espece particuliere de Mouvement non uniforme, fût la mesure premiere du tems plutôt qu’une autre : en second lieu, on ne pourroit mesurer le tems par un Mouvement non uniforme, sans avoir découvert auparavant par quelque moyen particulier l’analogie entre le rapport des tems & celui des espaces parcourus, qui conviendroit au Mouvement proposé. D’ailleurs, comment connoître cette analogie autrement que par l’expérience, & l’expérience ne supposeroit-elle pas qu’on eût déja une mesure du tems fixe & certaine ?

Mais le moyen de s’assurer, dira-t’on, qu’un Mouvement soit parfaitement uniforme ? Je réponds d’abord, qu’il n’y a non plus aucun Mouvement non uniforme dont nous sachions exactement la Loi, & qu’ainsi cette difficulté prouve seulement que nous ne pouvons connoître exactement & en toute rigueur le rapport des parties du tems ; mais il s’ensuit pas delà, que le Mouvement uniforme n’en soit par sa nature seule, la premiere & la plus simple mesure. Aussi ne pouvant avoir de mesure du tems précise & rigoureuse, c’est dans les Mouvemens à peu près uniformes que nous en cherchons la mesure au moins approchée. Nous avons trois moyens de juger qu’un Mouvement est à peu près uniforme : 1º. Quand le corps qui se meut parcourt des espaces égaux, dans des tems que nous avons lieu de juger égaux ; & nous avons lieu de juger les tems égaux, quand nous avons observé par une expérience réitérée, qu’il se passe durant ces tems des effets semblables, que nous avons lieu de juger devoir durer également long-tems. Ainsi nous avons lieu de juger que les tems qu’une même clepsydre met à se vuider sont égaux ; si donc pendant ces tems un corps parcourt des espaces égaux, nous avons lieu de juger que son mouvement est uniforme. 2º. Quand nous avons lieu de croire que l’effet de la cause accélératrice ou retardatrice, s’il y en a une, ne peut être qu’insensible. C’est par la réunion de ces deux moyens qu’on a jugé que le mouvement de la terre autour de son axe est uniforme, & cette supposition non-seulement n’est point contredite par les autres phénomenes célestes, mais elle paroît même s’y accorder parfaitement. 3º. Quand nous comparons le Mouvement dont il s’agit à d’autres Mouvemens, & que nous observons la même Loi dans les uns & les autres. Ainsi, si plusieurs Corps se meuvent, de maniere que les espaces qu’ils parcourent durant un même tems soient toujours entr’eux, ou exactement, ou à peu près dans le même rapport, on juge que le Mouvement de ces Corps est ou exactement, ou au moins à très-peu près uniforme. Car si un corps $A\,\!$ qui se meut uniformément parcourt l’espace $E\,\!$ durant le tems $T\,\!$ pris à volonté, & qu’un autre corps $B\,\!$, se mouvant aussi uniformément, parcoure l’espace $e\,\!$ pendant le même tems $T\,\!$, le rapport des espaces $E\,\!$, $e\,\!$, sera toujours le même soit que les deux corps ayent commencé à se mouvoir dans le même instant ou dans des instans différens ; & le mouvement uniforme est le seul qui ait cette propriété. C’est pourquoi si on divise le tems en parties quelconques égales ou inégales à volonté, & si on trouve que les espaces parcourus par deux corps durant une même partie de ce tems, sont toujours dans le même rapport, plus le nombre des parties du tems sera grand, plus on sera en droit de conclure que le mouvement de chaque corps est uniforme.

Aucun de ces trois moyens n’est exact dans la rigueur géométrique ; mais ils suffisent, surtout quand ils sont répétés & réunis, pour tirer une conc1usion valable, sinon sur l’uniformité absolue, au moins sur l’uniformité très-approchée.

13. Un Corps qui se meut uniformément est dit se mouvoir d’autant plus vîte, que l’espace $BD\,\!$ qu’il parcourt dans un même tems $AB\,\!$, est plus grand ; de sorte que si $BD\,\!$, $Bd\,\!$ sont les espaces parcourus uniformément par deux Corps dans le même tems $AB\,\!$, on dit que les vitesses de ces deux Corps sont entr’elles comme $BD\,\!$ à $Bd\,\!$.

Corollaire.

14. $BD\,\!$ est à $Bd::\,\!$ ${\frac {BD}{AB}}:{\frac {Bd}{AB}}::{\frac {BD}{AB}}:{\frac {Ce}{AC}}\,\!$ donc en général les vitesses de deux Corps sont entr’elles comme les espaces $BD\,\!$, $Ce\,\!$ q’ils parcourent dans des tems quelconques, ces espaces étant divisés par les tems employés à les parcourir^[2].

La vitesse d’un Corps mû uniformément, est donc en général comme l’espace divisé par le tems. La vitesse ne renfermant qu’une idée relative, n’a point de mesure absolue, on ne juge point de la vitesse d’un Corps en elle-même, mais en la comparant à la vitesse d’un autre Corps. Ainsi cette maniere de parler si commune chez les Mécaniciens, que la vitesse est égale à l’espace divisé par le tems, n’est qu’une expression abrégée pour dire que les vitesses de deux Corps qui se meuvent uniformément, sont entr’elles comme les espaces que ces Corps parcourent, divisés par les tems qu’ils employent à les parcourir ; expression qu’il faut entendre elle-même dans le sens expliqué par la note.

Du Mouvement accéléré ou retardé.

15. Si les lignes $BD\,\!$, $CE\,\!$, (Fig. 3 & 4) représen tant les espaces parcourus pendant les tems $AB\,\!$, $AC\,\!$, ne sont pas à une ligne droite, mais à une courbe $ADE\,\!$, alors le Mouvement n’est plus uniforme, mais il est accéléré ou retardé, selon que la courbe $ADE\,\!$ est convexe ou concave vers $AC\,\!$; car si le mouvement est accéléré, par exemple, les espaces $DX\,\!$, $PE\,\!$ (Pl. V. fig. 1.) parcourus dans des tems égaux $BQ\,\!$, $BC\,\!$, sont croissans ; ensorte que $PE\,\!$ eft $>DX\,\!$; ce qui ne sauroit être à moins que la courbe $ADE\,\!$ ne soit convexe vers $AC\,\!$. Cette variation continuelle ne peut provenir (art. 6.) que de quelque cause étrangere qui agit sans cesse, pour accélérer ou retarder le Mouvement.

Fig. 3

Fig. 4

Fig. V-1

La vitesse du Corps mû change alors à chaque instant, & ne peut avoir, comme dans le Mouvement uniforme, une quantité constante pour mesure. On conçoit seulement que son expression pour un instant donné, doit être la même qu’elle seroit, si dans cet instant le Mouvement cessoit d’être accéléré ou retardé. Supposons donc, par exemple, que le Mouvement du corps soit accéléré ; & qu’à l’instant même où le corps finit de parcourir la ligne $BD\,\!$, il vienne à se mouvoir uniformément avec la vitesse qu’il a en $D\,\!$; il est clair, 1º. que les lignes $TZ\,\!$, $PN\,\!$ (Pl. V. fig. 1.) représentant les espaces qu’il décriroit alors dans des tems finis quelconques $BM\,\!$, $BC\,\!$, seroient terminés par une ligne droite $DN\,\!$; 2º. que ces lignes $PN\,\!$, $TZ\,\!$, doivent être plus grandes que les espaces $DX\,\!$, $Dx\,\!$, qu’il a parcourus précédemment dans des tems $Bm=BM\,\!$, & $BQ=BC\,\!$; 3°. que ces mêmes espaces $PN\,\!$, $TZ\,\!$ doivent être plus petits que les espaces $PE\,\!$, $TG\,\!$, qu’il auroit parcourus dans les tems $BC\,\!$, $BM\,\!$, si son mouvement avoit continué à être accéléré. Or pour cela il faut que $DN\,\!$ soit tangente^[3]. On démontrera la même chose dans le cas du mouvement retardé ; d’où il s’ensuit, en général, en tirant la tangente $DN\,\!$, que $PN\,\!$ seroit l’espace que le corps parcourrait dans le tems $BC\,\!$ au lieu de $PE\,\!$. Dans ce cas (art. 14) ${\frac {PN}{DP}}\,\!$ exprimeroit sa vitesse ; or le rapport de $PN\,\!$ à $DP\,\!$, est le même que celui de l’Elément de $BD\,\!$ à l’Elément de $AB\,\!$, parce que $DN\,\!$ est tangente. Donc si on nomme en général $t\,\!$ le tems, $e\,\!$ l’espace correspondant parcouru par le corps, $u\,\!$ la vitesse à la fin du tems $t\,\!$, on aura $u={\frac {de}{dt}}\,\!$.

Si on prolonge la tangente $DN\,\!$ (Pl. I. fig. 3. & 4.) jusqu’à ce quelle rencontre $AB\,\!$ en $F\,\!$; $BF\,\!$ exprimera le tems que le corps employeroit à parcourir uniformément $BD\,\!$ avec la vitesse qu’il a au point $D\,\!$. Donc si par le point $A\,\!$ on tire $Ad\,\!$ parallèle à $FD\,\!$; $Bd\,\!$ sera l’espace que ce même corps parcourroit uniformément avec cette même vitesse dans le tems $AB\,\!$.

On voit par-là (Fig. 3) que si $ADE\,\!$, par exemple, est une parabole, c’est-à-dire, si les espaces $BD\,\!$, $CE\,\!$ sont entr’eux comme les quarrés des tems, on aura $AB=2BF\,\!$; & $Bd=2BD\,\!$.

Corollaire I.

16. Les espaces $NE\,\!$, $ne\,\!$, sont les espaces que le Corps parcourt pendant les tems $BC\,\!$, $Bc\,\!$, de plus ou de moins que les espaces $PN\,\!$, $pn\,\!$ qu’il eût parcourus uniformément avec la vitesse qu’il a en $D\,\!$. Or si on suppose les tems $BC\,\!$, $Bc\,\!$, infiniment petits, les lignes $NE\,\!$, $ne\,\!$, sont entr’elles comme le quarré de $BC\,\!$ au quarré de $Bc\,\!$. Car l’arc $DE\,\!$ à cause de sa petitesse infinie, peut être regardé comme un arc de cercle ; or soit $DN\,\!$ (Fig. 5) la partie infiniment petite de la tangente d’un arc de cercle ; & par le point $N\,\!$, & un autre point $n\,\!$ quelconque de cette partie, soient tirées à volonté les parallèles $NQ\,\!$, $nq\,\!$; on aura par la propriété du cercle $NE\times NQ=DN^{2}\,\!$; $ne\times nq=Dn^{2}\,\!$; & à cause que les lignes $nq\,\!$, $NQ\,\!$ doivent être regardées comme égales, on aura $NE:ne::DN^{2}:Dn^{2}\,\!$. Or (Fig. 3 & 4) $DN:Dn::BC:Bc\,\!$, & par conséquent en général $NE:ne::BC^{2}:Bc^{2}\,\!$.

Fig. 5

Corollaire II.

17. Il est clair que les espaces $NE\,\!$, $ne\,\!$, seroient ceux que la cause accéleratrice feroit parcourir au corps, dans les instans $BC\,\!$, $Bc\,\!$, si au commencement de ces instans il n’avait aucune vitesse. Donc les espaces parcourus par un corps en vertu d’une puissance accélératrice quelconque, sont au commencement du Mouvement comme les quarrés des tems.

Corollaire III.

18. Donc en regardant $BC\,\!$ ou $dt\,\!$ comme constant, on pourra supposer ${\frac {NE}{BC^{2}}}=F\,\!$, $F\,\!$ étant une quantité quelconque^[4] qui variera si l’on veut pour chaque abscisse $AB\,\!$, mais qui pourra être censée constante, tant que $AB\,\!$ ne variera qu’infiniment peu.

Corollaire IV.

19. Si dans un cercle quelconque $RDQ\,\!$ (Fig. 5) on tire les cordes infiniment petites $RD\,\!$, $DE\,\!$, lesquelles soient égales, ou différent l’une de l’autre d’une quantité infiniment petite par rapport à elles, & qu’on prolonge $RD\,\!$ en $O\,\!$ ensorte que $DO=RD\,\!$, qu’enfin on mene par les points $O\,\!$, $E\,\!$ la ligne $OQ\,\!$ & par le point $D\,\!$ la tangente $DN\,\!$ qui rencontre $OQ\,\!$ en $N\,\!$; on aura par la propriété du cercle $DN^{2}=NE\times NQ\,\!$; $OD\times OR\,\!$ ou $2DO^{2}=OE\times OQ\,\!$; donc à cause que les lignes $DN\,\!$ & $DO\,\!$, $NQ\,\!$ & $OQ\,\!$ doivent être regardées comme égales, on aura $OE=2NE\,\!$^[5].

Donc si on considere l’Elément $DE\,\!$ d’une courbe quelconque $ADE\,\!$ (Fig. 3 & 4) comme un petit arc de cercle, ce qu’on peut supposer sans erreur, il s’en suit que la différence seconde $OE\,\!$ de l’espace parcouru est double de l’espace réel $NE\,\!$, que la puissance accélératrice ou retardatrice feroit parcourir au corps dans l’instant $BC\,\!$; quoique ces deux lignes $OE\,\!$, $NE\,\!$ paroissent être égales dans la courbe considérée comme polygone, parce qu’alors la tangente $DN\,\!$ se confond avec le prolongement $DO\,\!$ du petit côté $RD\,\!$ de la courbe.

Corollaire V.

20. Donc si on appelle $e\,\!$ l’espace parcouru $BD\,\!$ pendant le tems $t\,\!$, on aura $dde=2NE\,\!$, & puifque ${\frac {NE}{BC^{2}}}=F\,\!$, on aura ${\frac {dde}{dt^{2}}}=2F\,\!$; donc en général l’on peut sup poser que l’équation différentio-différentielle de la Courbe $ADE\,\!$ est $\varphi dt^{2}=\pm dde\,\!$, $\varphi \,\!$ exprimant une fonction quelconque de $e\,\!$ & de $t\,\!$, ou même de ces grandeurs & de leurs différences ; le signe $+\,\!$ étant pour le cas où le Mouvement est accéléré, c’est-à-dire, ou la courbe $ADE\,\!$ est convexe vers $AC\,\!$, & le signe $-\,\!$ pour le cas où le Mouvement est retardé, c’est-à-dire, ou la courbe $ADE\,\!$ est concave vers $AC\,\!$.

Corollaire VI.

21. Puisque (art. 15) $u={\frac {de}{dt}}\,\!$, on aura à cause de $dt\,\!$ constant, $dde=dudt\,\!$; donc l’équation précédente $\varphi dt^{2}=\pm dde\,\!$ se changera en celle-ci $\varphi dt=\pm du\,\!$, ou $\varphi de=\pm udu\,\!$.

Remarques sur les forces accélératrices, & sur la comparaison de ces forces entr’elles.

Remarque I.

22. Le Mouvement uniforme d’un Corps ne peut être altéré que par quelque cause étrangere. Or de toutes les causes, soit occasionnelles, soit immédiates, qui influent dans le Mouvement des corps, il n’y a tout au plus que l’impulsion seule dont nous soyons en état de déterminer l’effet par la seule connoissance de la cause, comme on le verra dans la seconde Partie de cet Ouvrage. Toutes les autres causes nous sont entiérement inconnues ; elles ne peuvent par conséquent se manifester à nous, que par l’effet qu’elles produisent en accélérant ou retardant le Mouvement des corps, & nous ne pouvons les distinguer les unes des autres que par la loi & la grandeur connue de leurs effets, c’est-à-dire, par la loi & la quantité de la variation qu’elles produisent dans le Mouvement. Donc, lorsque la cause est inconnue, ce qui est le seul cas dont il soit question ici, l’équation de la courbe $ADE\,\!$ doit être donnée immédiatement, ou en termes finis, ou en quantités différentielles. L’équation est donnée ordinairement en différences, lorsque le Mouvement est accéléré ou retardé suivant une loi arbitraire & de pure hypothese. Elle est au contraire donnée ordinairement en termes finis, quand la loi du rapport des espaces aux tems est découverte par l’expérience. Ainsi supposons que la puissance qui accélere, soit telle que le corps reçoive continuellement dans des instans égaux des degrés égaux de vitesse ; alors $dt\,\!$ étant constant, $du\,\!$ le sera aussi, & par conséquent $\varphi \,\!$ sera une quantité constante. L’équation $\varphi dt=du\,\!$ sera en ce cas donnée immédiatement par hypothose. Supposons, au contraire, que dans un cas particulier on découvre par l’expérience que les espaces finis parcourus depuis le commencement du Mouvement, sont comme les quarrés des tems employés à les parcourir, l’équation de la courbe $ADE\,\!$ sera $e={\frac {at^{2}}{T^{2}}}\,\!$, $a\,\!$ étant l’espace parcouru pendant un tems constant quelconque $T\,\!$; d’où l’on tire $dde={\frac {2adt^{2}}{T^{2}}}\,\!$ & $du={\frac {2adt}{T^{2}}}\,\!$. On voit par-là que dans cette supposition les accroissemens de vitesse à chaque instant sont égaux, ce qu’on exprime autrement en disant que la force accélératrice $\varphi \,\!$ est constante ; ainsi dans ce cas & dans d’autres semblables, les équations différentielles $\varphi dt^{2}=\pm dde\,\!$, $\varphi dt=\pm du\,\!$, se tirent de l’équation donnée de la courbe $ADE\,\!$ en termes finis.

Il est donc évident que quand la cause est inconnue, l’équation $\varphi dt=\pm du\,\!$ est toujours donnée^[6].

La plûpart des Géometres présentent sous un autre point de vûe l’équation $\varphi dt=du\,\!$ entre les tems & les vitesses. Ce qui n’est, selon nous, qu’une hypothese, est érigé par eux en principe. Comme l’accroissement de la vitesse est l’effet de la cause accélératrice, & qu’un effet, selon eux, doit être toujours proportionnel à sa cause, ces Géometres ne regardent pas seulement la quantité $\varphi \,\!$ comme la simple expression du rapport de $du\,\!$ à $dt\,\!$; c’est de plus, selon eux, l’expression de la force accélératrice, à laquelle ils prétendent que $du\,\!$ doit être proportionnel, $dt\,\!$ étant constant ; de là ils tirent cet axiome général, que le produit de la force accélératrice par l’élément du tems est égal à l’élément de la vitesse. M. Daniel Bernoulli (Mém. de Petersb. To. I.) prétend que ce principe est seulement de vérité contingente, attendu qu’ignorant la nature de la cause & la maniere dont elle agit, nous ne pouvons savoir si son effet lui est réellement proportionnel, ou s’il n’est pas comme quelque puissance ou quelque fonction de cette même cause. M. Euler, au contraire, s’est efforcé de prouver fort au long dans sa Mécanique, que ce principe est de vérité nécessaire. Pour nous, sans vouloir discuter ici si ce principe est de vérité nécessaire ou contingente, nous nous contenterons de le prendre pour une définition, & d’entendre seulement par le mot de force accélératrice, la quantité à laquelle l’accroissement de la vitesse est proportionnel. Ainsi au lieu de dire que l’accroissement de vitesse à chaque instant est constant, ou que cet accroissement est comme le quarré de la distance du corps à un point fixe, ou &c. nous dirons simplement pour abréger & pour nous conformer d’ailleurs au langage ordinaire, que la force accélératrice est conftante, ou qu’elle est comme le quarré de la distance, ou &c. & en général, nous ne prendrons jamais le rapport de deux forces que pour celui de leurs effets, sans examiner si l’effet est réellement comme sa cause, ou comme une fonction de cette cause : examen entierement inutile, puisque l’effet est toujours donné indépendamment de la cause, ou par expérience, ou par hypothese.

Ainsi nous entendrons en général par la force motrice le produit de la masse qui se meut par l’élément de sa vitesse, ou, ce qui est la même chose, par le petit espace qu’elle parcourroit dans un instant donné en vertu de la cause qui accélere ou retarde son Mouvement ; par force accélératrice, nous entendrons simplement l’élément de la vitesse. Après de pareilles définitions, il est aisé de voir que tous les Problêmes qu’on peut proposer sur le Mouvement des Corps mûs en ligne droite, & animés par des forces qui tendent vers un centre, ou exerçant les uns sur les autres une attraction mutuelle suivant une loi quelconque, sont des problêmes qui appartiennent pour le moins autant à la Géométrie qu’à la Mécanique, & dans lesquels la difficulté n’est que de calcul, pourvû que le mobile soit regardé comme un point.

On imagineroit peut-être que l’équation $\varphi dt=\pm du\,\!$ regardée, non comme hypothese, mais comme principe, seroit au moins nécessaire pour calculer les effets dont les causes sont connues, comme l’impulsion, surtout quand cette impulsion consiste en de petits coups réïtérés. J’espere qu’on verra dans la seconde Partie de cet Ouvrage, que non-seulement ce prétendu principe est encore inutile dans ce cas, mais que l’application en est insuffisante & pourroit même être fautive.

Remarque II.

23. Il n’est pas inutile de remarquer que quand on a d’abord l’équation entre $e\,\!$ & $t\,\!$ en termes finis, & qu’on en tire par la différentiation à l’ordinaire l’équation $dde=\varphi dt^{2}\,\!$, la valeur de $dde\,\!$ qu’on trouve par ce calcul est précisément celle de $OE\,\!$, véritable différence seconde de $BD\,\!$; on pourroit d’abord douter^[7], vû la nature même du calcul différentiel, si la valeur de $dde\,\!$ trouvée par cette différentiation représente véritablement $OE\,\!$, ou quelque autre ligne, par exemple $NE\,\!$. Mais on peut se convaincre par le calcul même que la quantité trouvêe $\varphi dt^{2}\,\!$ est égale à $OE\,\!$.

Remarque III.

24. Nous avons vû ci-dessus (art. 15) que quand les

espaces parcourus sont comme les quarrés des tems correspondans, un Corps qui parcourt un espace $E\,\!$ dans le tems $T\,\!$, parcourroit uniformément dans le même tems l’espace $2E\,\!$ avec la vitesse qu’il a à l’extrémité de l’espace $E\,\!$. Or quelle que soit la puissance accélératrice ou retardatrice, les espaces $ne\,\!$, $NE\,\!$ parcourus en vertu de cette puissance, durant les instans $Bc\,\!$, $BC\,\!$, sont entr’eux comme les quarrés de ces instans. D’où il s’ensuit que dans la courbe polygone, $OE\,\!$ ou $dde=2NE\,\!$ considérée comme l’effet de la puissance accélératrice ou retardatrice, doit être regardée comme parcourue d’un mouvement uniforme avec la vitesse infiniment petite que le corps a acquis à la fin de l’instant $BC\,\!$. On voit par-là de quelle maniere on peut réduire à un mouvement uniforme l’effet instantané de la puissance qui accélere ou qui retarde le mouvement.

Remarque IV.

25. Dans la courbe polygone les effets de la force accélératrice pendant les instans $Bc\,\!$, $BC\,\!$ (Pl. V. fig. 3} sont représentés par les lignes $O'E'\,\!$, $OE\,\!$; ces espaces $O'E'\,\!$, $OE\,\!$ sont évidemment entr’eux comme les tems $Bc\,\!$, $BC\,\!$, à cause des triangles semblables $DE'O'\,\!$, $DEO\,\!$, & cette proposition sert à confirmer ce que nous venons de remarquer, que l’espace $OE\,\!$ est censé parcouru uniformément pendant le tems $BC\,\!$; car quand les espaces $O'E'\,\!$, $OE\,\!$ sont entr’eux comme les tems $Bc\,\!$, $BC\,\!$ employés à les parcourir, le mouvement est uniforme.

Fig. V-3

De là il s’ensuit, que puisque dans la courbe polygone l’effet de la puissance accélératrice est représenté par un mouvement uniforme, on ne doit point supposer dans cette hypothese que la vitesse du corps s’accélere par degrés pendant l’instant $BC\,\!$, mais qu’au commencement de cet instant $BC\,\!$, lorsque le corps a parcouru l’espace $BD\,\!$, sa vitesse reçoive brusquememt & comme d’un seul coup toute l’augmentation ou la diminution qu’elle ne doit réellement avoir qu’à la fin de l’instant $BC\,\!$.

Pour confirmer cette remarque, on peut observer que $TE'\,\!$, $RE\,\!$ (Pl. V. fig. 2.) sont les espaces que le corps parcourt réellement durant les instans $Bc\,\!$, $BC\,\!$, dans l’hypothese de la courbe polygone ; que ces espaces sont parcourus uniformément, puisqu’ils sont entr’eux comme les tems $Bc\,\!$, $BC\,\!$; qu’ainsi la vitesse pendant l’instant $BC\,\!$ est censée uniforme, & qu’elle est à la vitesse dans l’instant précédent $BM\,\!$ comme $RE\,\!$ est à $ID\,\!$. D’où il s’ensuit qu’au commencement de l’instant $BC\,\!$, la vitesse change brusquement, suivant le rapport de $RE\,\!$ à $ID\,\!$.

Au contraire dans la courbe rigoureuse, les effets de la puissance accélératrice ou retardatrice pendant les instans $Bc\,\!$, $BC\,\!$, sont représentés par $ne\,\!$, $NE\,\!$ (Pl.V. fig. 3.) & sont entr’eux, comme les quarrés de ces instans ; dans ce cas la vitesse est censée s’accélérer ou se retarder uniformément pendant tout le cours de l’instant $BC\,\!$, en vertu de la puissance accélératrice, qui est censée donner au mobile pendant cet instant une suite de pe tits coups égaux & réitérés ; & la somme de ces petits coups est égale au coup unique, que la même puissance est censée donner au corps dès le commencement de l’instant $BC\,\!$ dans l’hypothese de la courbe polygone.

On pourrait faire ici une difficulté qu’il est bon de prévenir. L’équation trouvée $dde=\varphi dt^{2}\,\!$ appartient à la courbe rigoureuse & à la courbe polygone^[8] ; donc puisque $\varphi \,\!$ est regardée comme constante pendant l’instant $BC\,\!$, $dde\,\!$ ou $OE\,\!$ est proportionnelle à $dt^{2}\,\!$, c’est-à-dire au quarré de $BC\,\!$, même dans la courbe polygone ; cependant nous venons de voir que les lignes $E'O'\,\!$, $EO\,\!$ sont proportionnelles aux lignes $Bc\,\!$, $BC\,\!$. Comment accorder ces deux propositions ? La réponse est très-simple ; c’est que $E'O'\,\!$ n’est pas le $dde\,\!$ qui répond à l’instant $Bc\,\!$; comme il est facile de s’en assurer^[9] par la seule inspection de la figure 3. Planche V.

Remarque V.

26. Les Géometres doivent prendre garde à cette distinction des courbes polygones & des courbes rigoureuses, dans l’estimation des effets des forces accélératrices & dans la comparaison de ces effets entr’eux. Si un des effets est calculé dans l’hypothese de la courbe rigoureuse, il faut calculer l’autre dans la même hypothese ; autrement on courroit risque de faire le rapport des forces, c’est-à-dire de leurs effets, double de ce qu’il est réellement^[10].

Remarque VI.

27. Si on suppose une puissance accélératrice constante $p\,\!$ telle que la pesanteur, en vertu de laquelle un corps parcourre l’espace fini $z\,\!$ pendant le tems fini $\theta \,\!$, on aura $\varphi :p::{\frac {dde}{dt^{2}}}:{\frac {2z}{\theta ^{2}}}\,\!$^[11], ou $\varphi :p::{\frac {NE}{dt^{2}}}:{\frac {z}{\theta ^{2}}}\,\!$. Donc $\varphi dt^{2}={\frac {pdde.\theta ^{2}}{2z}}\,\!$ ou $dde={\frac {2\phi zdt^{2}}{p\theta ^{2}}}\,\!$, & $NE={\frac {\phi zdt^{2}}{\theta ^{2}}}\,\!$.

Il faut se donner de garde d’écrire $dde={\frac {\phi zdt^{2}}{p\theta ^{2}}}\,\!$, comme on pourrait y être porté en prenant $dde\,\!$ pour $NE\,\!$; car il est évident que par cette opération on n’auroit que la moitié de la valeur de $dde\,\!$ qui est égal à $2NE\,\!$; ainsi en intégrant on n’auroit que la moitié de la valeur de $e\,\!$. Veut-on s’en assurer par un exemple simple ? Qu’on suppose $\varphi =p\,\!$, c’est-à-dire la puissance constante & égale à la pesanteur ; on fait que les espaces $e\,\!$, $z\,\!$, sont alors entr’eux comme les quarrés des tems $t^{2}\,\!$, $\theta ^{2}\,\!$, donc on a $e={\frac {zt^{2}}{\theta ^{2}}}\,\!$, & c’est ce que donne en effet (quand on l’integre) l’équation $dde={\frac {2\phi zdt^{2}}{p\theta ^{2}}}\,\!$ ou $dde={\frac {2zdt^{2}}{\theta ^{2}}}\,\!$:au lieu que l’équation $dde={\frac {zdt^{2}}{\theta ^{2}}}\,\!$ ne donneroit que $e={\frac {zt^{2}}{2\theta ^{2}}}\,\!$, c’est-à-dire la moitié de la valeur de $e\,\!$.

1. On trouvera dans l’Encyclopédie au mot Force plusieurs autres réflexions sur le principe de la force d’inertie ; comme elles n’appartiennent pas immédiatement à notre sujet, nous y renvoyons le Lecteur.
2. L’espace & le tems étant des quantités de nature différente, ainsi qu’on l’a remarqué dans le Discours préliminaire, on sent bien qu’on ne peut diviser l’espace par le tems ; ainsi quand on dit que les vitesses sont comme les espaces divisés par les tems, c’est une expression abrégée qui signfie que les vitesses sont comme les rapports des espaces à une même commune mesure, divisés par les rapports des tems à une même commune mesure ; c’est-à-dire que si on prend, par exemple, le pied pour la mesure des espaces, & la minute pour la mesure des tems, les vitesses de deux corps qui se meuvent uniformément sont entr’elles comme les nombres de pieds parcourus divisés par les nombres de minutes employées à les parcourir, & non pas comme les pieds divisés par les minutes. Voyez l’Encyclopédie à la fin du mot Equation.
3. Il est visible qu’on ne peut supposer que le corps décrive par son mouvement uniforme un espace $PO\,\!$ plus petit que l’espace $PN\,\!$ terminé par la tangente $DN\,\!$; car $PO\,\!$ seroit alors plus petit que $DX\,\!$, puisque $PO=Dy\,\!$. On ne peut supposer non plus qu’il décrive un espace $PR\,\!$ plus grand que $PN\,\!$, car alors on pourrait toujours supposer le point $T\,\!$ tellement placé, que l’espace $TG'\,\!$ parcouru uniformément pendant le tems $DT\,\!$ fût plus grand que l’espace $TG\,\!$ terminé à la courbe, ce qui ne se peut.
4. La proportion $NE:ne::BC^{2}:Bc^{2}\,\!$ donne ${\frac {NE}{BC^{2}}}={\frac {ne}{Bc^{2}}}\,\!$; done si ${\frac {NE}{BC^{2}}}\,\!$ est exprimé par $F\,\!$, ${\frac {ne}{Bc^{2}}}\,\!$ sera aussi exprimé par $F\,\!$, $F\,\!$ gardant la même valeur, & par conséquent $F\,\!$ reste la même lorsque $AB\,\!$ varie infiniment peu.
5. Lorsque les lignes $OD\,\!$, $DE\,\!$, sont égales, on peut démontrer rigoureusement que $OE=2NE\,\!$. Car le triangle $DOE\,\!$ est isoscele, l’angle $ODE\,\!$ a pour mesure la moitié de l’arc $RDE\,\!$, & l’angle $NDE\,\!$ la moitié de l’arc $DE\,\!$. D’où il s’ensuit que $DN\,\!$ divise l’angle $ODE\,\!$ en deux également, & qu’ainsi à cause de $DO=DE\,\!$, on a $OE=2NE\,\!$:mais la démonstration que nous avons donnée dans le texte, s’étend encore au cas où $OD\,\!$, $DE\,\!$ différeroient d’une quantité infiniment petite par rapport à elles, & par conséquent ne seroient pas rigoureusement égales.
6. On vient de voir que de quelque maniere que le mouvement soit accéléré ou retardé, l’équation différentio-différentielle de la courbe sera toujours de cette forme $\pm dde=\varphi dt^{2}\,\!$. Or si on veut faire usage de cette équation, ainsi que des équations $\varphi dt=\pm du\,\!$ & $\varphi de=\pm udu\,\!$ pour déterminer dans un mouvement quelconque la relation entre $u\,\!$, $t\,\!$, $e\,\!$, il faut connoître $\varphi \,\!$, & l’on pourrait penser que pour cet effet la connoissance de la cause qui accélere ou retarde le mouvement seriit nécessaire ; l’objet de la Remarque est de faire voir que non, mais que $\varphi \,\!$ est toujours donné par la définition même de l’espece de mouvement dont il est question ; ainsi, conformément à cette même Remarque, quand on voudra faire usage des équations $\varphi dt^{2}=\pm dde\,\!$, $\varphi dt=\pm du\,\!$ & $\varphi de=\pm udu\,\!$ pour déterminer la relation des espaces, des vitesses & des tems dans un mouvement dont la loi sera donnée, il suffira de substituer dans ces équations à la place de $\varphi \,\!$ une quantité propre à exprimer la loi suivant laquelle on supposera que se font les augmentations ou diminutions de vitesse : quand on supposera, par exemple, que les diminutions instantanées de vitesse sont comme les quarrés de la vitesse, on écrira $gu^{2}dt=-du\,\!$, $gu^{2}de=-udu\,\!$ ($g\,\!$ étant un coefficient constant), & ainsi du reste.
7. Il suffit pour former ce doute de se rappeller le principe d’après lequel on trouve les différences secondes. Supposant $AM=t\,\!$ (Pl. V. fig. 2) & $MP=\,\!$ une fonction de $t\,\!$ que je représente par $\phi (t)\,\!$; pour avoir $ID\,\!$ on suppose que $t\,\!$ devienne $t+dt\,\!$, & alors $BD\,\!$ étant $=\phi (t+dt)\,\!$, on a $ID=\phi (t+dt)-\phi (t)\,\!$ en négligeant les quantités infiniment petites du second ordre & des ordres ultérieurs. Ensuite pour avoir $EO\,\!$ on suppose dans la valeur de $ID\,\!$ que $t\,\!$ devienne $t+dt\,\!$, & on néglige dans ce calcul les quantités infiniment petites du troisieme ordre & des ordres ultérieurs pour avoir la valeur de $RE\,\!$, ensorte qu’on prend pour $dde\,\!$ la différence entre cette valeur de $RE\,\!$, & celle qu’on a trouvé pour $ID\,\!$. Mais il faut remarquer que puisque dans la valeur de $ID\,\!$ on a négligé les quantités du second ordre, cette omission peut influer sur la différence cherchée des lignes $ID\,\!$, $RE\,\!$, laquelle différence est infiniment petite du second ordre, par conséquent on n’est en droit de conclure que $OE\,\!$ est égal à la valeur de $dde\,\!$, qu’autant qu’on aura fait voir que l’omission dont il s’agit, ne produit dans le calcul qu’une erreur infiniment petite au-dessous du second ordre.

   

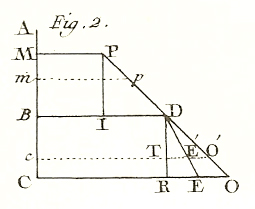
   Fig. V-2

   Pour y parvenir nous allons d’abord démontrer une proposition que notre Auteur a donnée dans ses recherches sur le systême du monde. Soit $\phi (z+\xi )\,\!$ une fonction de $z+\xi \,\!$, $\xi \,\!$ étant une quantité très-petite dont on suppose que $z\,\!$ augmente, on aura. $\phi (z+\xi )=\phi (z)+\xi \Delta (z)+{\frac {\xi ^{2}\Gamma (z)}{2}}+\,\!$ &c. $\Delta (z)\,\!$ étant le coefficient de $dz\,\!$ dans la différentiation de $\phi (z)\,\!$, & $\Gamma (z)\,\!$ celui de $dz\,\!$ dans la différentiation de $\Delta (z)\,\!$. Car si on suppose $\phi (z+\xi )=\phi (z)+u\,\!$ & qu’on différentie en supposant $z\,\!$ constant (ce qui est permis ici, puisqu’on suppose que $z\,\!$ ne croît actuellement que de la quantité $\xi \,\!$) on aura $d\xi \Delta (z+\xi )=du\,\!$; soit $\Delta (z+\xi )=\Delta (z)+r\,\!$, on aura $d\xi \Gamma (z+\xi )=dr\,\!$; soit $\Gamma (z+\xi )=\Gamma (z)+s\,\!$, on aura $d\xi \Pi (z+\xi )=ds\,\!$, donc en continuant de la même maniere, on aura $\phi (z+\xi )=\phi (z)+\int d\xi \Delta (z)+\int d\xi \int d\xi \Gamma (z)+\int d\xi \int d\xi \int d\xi \Pi (z)\,\!$ &c. $=\phi (z)+\xi \Delta (z){\frac {\xi ^{2}\Gamma (z)}{2}}+{\frac {\xi ^{3}\Pi (z)}{2\cdot 3}}+\,\!$ &c.

   Cela posé, $MP\,\!$ étant $=\phi (t)\,\!$ on a

   $BD=\phi (t+dt)=\phi (t)+dt\Delta (t)+{\frac {dt^{2}\Gamma (t)}{2}}+\,\!$ &c.

   $CE=\phi (t+2dt)=\phi (t)+2dt\Delta (t)+2dt^{2}\Gamma (t)+\,\!$ &c.

   Donc $ID=dt\Delta (t)+{\frac {dt^{2}\Gamma (t)}{2}}\,\!$

   $RE=dt\Delta (t)+{\frac {3}{2}}dt^{2}\Gamma (t)\,\!$

   $RE-ID\,\!$ ou $-OE\,\!$ ou $-dde=dt^{2}\Gamma (t)\,\!$.

   Mais par les méthodes ordinaires du calcul différentiel, on auroit

   $ID=dt\Delta (t)\,\!$

   $RE=dt\Delta (t+dt)=dt\Delta (t)+dt^{2}\Gamma (t)\,\!$

   donc $RE-ID\,\!$ ou $-OE\,\!$ ou $-dde=dt^{2}\Gamma (t)\,\!$.

   Donc le $dde\,\!$ que donne le calcul différentiel est en effet la vraie valeur de $OE\,\!$.

8. Note Wikisource : Correction d’auteur dans Fautes à corriger.
9. Il faut remarquer que ce qui détermine $EO\,\!$ pour la différence seconde de la ligne $MP\,\!$, c’est la supposition que les trois points $P\,\!$, $D\,\!$, $E\,\!$ soient à la courbe rigoureuse ; or $PD\,\!$, $DE\,\!$ étant considérées comme soutendantes de cette courbe, il est impossible que le point $E'\,\!$ lui appartienne, ainsi $E'O'\,\!$ n’est point le $dde\,\!$ qui répond à $Bc\,\!$. $EO\,\!$ étant supposé le $dde\,\!$ qui répond à $BC\,\!$, pour déterminer celui qui répond à $Bc\,\!$, il faut prendre $Bm=Bc\,\!$, & ayant tiré $mp\,\!$ parallèle à $BD\,\!$, qui rencontre la courbe en $p\,\!$, on tirera $pDo\,\!$, qui rencontre en $o\,\!$ la ligne $ceo\,\!$ parallèle à $BD\,\!$, & alors $eo\,\!$ sera le $dde\,\!$ qui répond à $Bc\,\!$; il y aura seulement cette différence, que la courbe polygone, au lieu d’être considérée comme ayant $DP\,\!$ & $DE\,\!$ pour côtés contigus, sera considérée comme ayant $Dp\,\!$ & $De\,\!$ pour côtés ; par conséquent ($DN\,\!$ étant la tangente de la courbe rigoureuse au point $D\,\!$, & $oe\,\!$ double de $ne\,\!$) puis’qu’on a $NE:ne::BC^{2}:Bc^{2}\,\!$, on a aussi $OE:oe::BC^{2}:Bc^{2}\,\!$; ainsi les $dde\,\!$ sont toujours comme les $dt^{2}\,\!$, & les lignes $OE\,\!$, $O'E'\,\!$ terminées à la courbe polygone & à sa tangente restent comme les $dt\,\!$.
10. On peut estimer l’effet d’une cause accélératrice de deux manieres, ou par l’espace qu’elle fait naturellement parcourir dans un instant, ou par celui que le corps pourroit parcourir pendant un instant égal avec la vitesse acquise pendant ce premier instant, continuée uniformément. Dans le premier cas, $NE\,\!$ (fig. 3. & 4.) marque cet effet, $DN\,\!$ étant tangente de la courbe rigoureuse ; dans le second cas, l’effet est marqué par $OE\,\!$ double de $NE\,\!$, $DO\,\!$ étant tangente de la courbe polygone. On est maître d’estimer l’effet de la cause accélératrice de l’une ou de l’autre de ces deux manieres ; mais lorsqu’on aura deux causes accélératrices à comparer, il faudra observer que si on a exprimé un des effets par $NE\,\!$ dans la courbe qui représente les espaces que l’une fait décrire, l’autre effet soit de même exprimé dans sa courbe correspondante par la ligne correspondante ; & c’est là ce qu’on entend lorsqu’on dit que si un des effets a été calculé dans l’hypothese de la courbe rigoureuse, l’autre doit être calculé dans la même hypothese &c.
11. On se propose dans cette Remarque de comparer toute force accélératrice à la pésanteur ; & voici le fondement de cette comparaison : l’équation $\phi dt^{2}=dde\,\!$ donne $\phi ={\frac {dde}{dt^{2}}}\,\!$; par la même raison $p={\frac {ddz}{d\theta ^{2}}}\,\!$; mais au lieu du rapport ${\frac {ddz}{d\theta ^{2}}}\,\!$ on peut substituer un rapport de quantités finies, en observant que les espaces parcourus naturellement en vertu d’une puissance accélératrice constante, sont comme les quarrés des tems ; ainsi on a $d\theta ^{2}:\theta ^{2}::{\frac {ddz}{2}}:z\,\!$; (on observera que nous avons mis ${\frac {ddz}{2}}\,\!$ dans la proportion, & non pas $ddz\,\!$ parce que $ddz\,\!$, comme on l’a déja dit, est double de l’espace réel, que la puissance seroit naturellement parcourir pendant l’instant $d\theta \,\!$.) On aura donc ${\frac {ddz}{d\theta ^{2}}}={\frac {2z}{\theta ^{2}}}\,\!$, & par conséquent $\phi :p::{\frac {dde}{dt^{2}}}:{\frac {2z}{\theta ^{2}}}\,\!$, ce qu’on peut encore démontrer d’une autre maniere ; car en intégrant l’équation $pd\theta ^{2}=ddz\,\!$ on a l’équation $p\theta ^{2}=2z\,\!$, qui étant comparée à l’équation $dde=\theta dt^{2}\,\!$ donne la même proportion.