Œuvres de Pierre Curie/43
SUR LA DISPARITION DE LA
RADIOACTIVITÉ INDUITE PAR LE RADIUM
SUR LES CORPS SOLIDES.
séance du 9 février 1903.
Les corps solides soumis à l’émanation du radium dans une enceinte close s’activent tous de la même façon. Retirés de l’enceinte et soustraits ainsi à l’action de l’émanation, ils se désactivent suivant une loi relativement rapide qui fait l’objet de la présente Note.
La loi de disparition de l’activité rayonnante est la même, quelle que soit la durée du séjour du corps dans l’enceinte, pourvu que ce séjour ait été suffisamment prolongé (durées d’activation supérieures à 24 heures). En général, la nature des corps n’intervient pas, et, placés dans les mêmes conditions, les corps s’activent et se désactivent tous de la même façon.
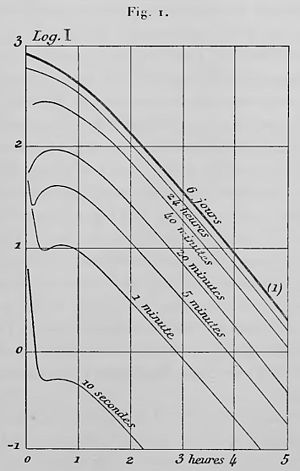
La loi de désactivation est représentée par la courbe (1) (traits épais) des figures 1 et 2. Le temps compté à partir du moment où l’on retire la lame de l’enceinte est porté en abscisses et le logarithme de l’intensité du rayonnement en ordonnées. On voit que la courbe représentative du phénomène devient sensiblement une droite après 2 heures 30 minutes de désactivation. À partir de ce moment l’intensité I du rayonnement décroît donc en fonction du temps suivant une loi exponentielle de la forme avec secondes. L’activité diminue de moitié en 28 minutes. Nous considérons cette loi de diminution de l’activité comme caractéristique de la forme sous laquelle l’énergie radioactive est emmagasinée à la surface des corps solides.
L’intensité du rayonnement à un moment quelconque est représentée par la différence de deux exponentielles
étant l’intensité initiale, secondes étant la constante de temps précédemment citée, secondes une nouvelle constante de temps. Le coefficient numérique a = 4,20.
L’énergie radioactive disparaît donc beaucoup plus rapidement
lorsqu’elle est sous la forme où elle se trouve sur un corps solide activé que lorsqu’elle est sous la forme d’émanation. Elle diminue
en effet, dans ce dernier cas, de moitié en 4 jours.
Lorsque la durée d’activation est inférieure à 24 heures, la loi de désactivation pendant les premières heures est fortement altérée ; on a indiqué (fig. 1) les courbes représentatives de désactivation. Les temps de séjour dans l’enceinte activante sont inscrits sur chaque courbe[1].
Pour une activation ayant duré 5 minutes, par exemple, l’intensité du rayonnement, après une baisse brusque, passe par un minimum (t = 8 min.), croît ensuite jusqu’à un maximum (t = 40 min.), puis décroît ensuite régulièrement. On voit sur la figure la manière dont se transforme la loi de désactivation en fonction du temps d’activation. Dans tous les cas, la loi de désactivation devient finalement, au bout de 2 heures 30 minutes, la loi exponentielle ordinaire avec baisse de moitié en 28 minutes. La courbe (1), qui représente la loi de désactivation après un temps long d’exposition à l’émanation, est la courbe normale limite.
Si l’on active un corps solide en le mettant brusquement au contact de l’émanation du radium, son rayonnement s’établit peu à peu et tend vers une valeur limite (La courbe en fonction du temps est alors identique à la courbe (1). Ainsi, que la lame s’active ou se désactive, le rayonnement tend vers sa valeur limite suivant la même loi. Les corps activés, lorsqu’on les sort d’une enceinte activante, ont la propriété d’émettre eux-mêmes, pendant quelque temps, de l’émanation radioactive capable d’activer d’autres corps mis dans leur voisinage. Cette propriété se perd assez rapidement et ne se manifeste plus au bout de 1 heure ou 2 heures, alors que l’activité des lames est encore très forte. Ce phénomène ne semble donc pas jouer le rôle principal dans la désactivation des lames. Peut-être est-ce dans la présence et dans la transformation d’une certaine quantité d’émanation qu’il faut rechercher l’explication des singularités des courbes au début de la désactivation.
Nous avons vu qu’en général la loi de désactivation ne dépend pas de la nature des corps activés : l’aluminium, le cuivre, le plomb, le bismuth, le platine, l’argent, le verre, l’alun, la paraffine se comportent de même. Cependant, pour certains corps qui
ont subi une activation longue, la loi exponentielle finale de désactivation ne s’applique plus. Après quelques heures, l’activité ne
décroît plus que fort lentement et demande quelquefois plusieurs jours pour diminuer de moitié. Le phénomène est extrêmement manifeste avec le celluloïd et le caoutchouc. La paraffine et la cire le présentent

à un degré moindre ; il se fait déjà sentir avec l’alun et le plomb. On voit (fig. 2) comment les courbes s’écartent de la courbe de désactivation normale (dans la construction de ces courbes, et pour les rendre comparables, on a supposé que l’intensité du rayonnement était la même au bout de 1 heure de désactivation). Le celluloïd a, de plus, la propriété d’émettre de l’émanation pendant plusieurs jours ; cependant, il finit par se désactiver complètement.
- ↑ M. Rutherford (Physikal. Zeitsch., 15 mars 1902) a déjà signalé les anomalies du début de la courbe de désactivation.



![{\displaystyle I\quad =\quad I_{0}{\Bigg [}ae^{-{\frac {t}{\theta _{1}}}}-(a-1)e^{-{\frac {t}{\theta _{2}}}}{\Bigg ]}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/f5a060dbd0e8592f55c28b4d6873487648e1eecd)




