Traité de la lumière/Chapitre V

Christian Huyghens

Traité de la lumière

Gauthier-Villars, 1920 (p. 62-125).

CHAPITRE V

DE L’ÉTRANGE RÉFRACTION DU CRISTAL D’ISLANDE

---

1. L’on apporte d’Islande, qui est une île de la Mer Septentrionale, à la hauteur de 66 degrés, une espèce de cristal, ou pierre transparente, fort remarquable par sa figure, et autres qualités, mais surtout par celles de ses étranges réfractions. Dont les causes m’ont semblé d’autant plus dignes d’être curieusement recherchées, que parmi les corps diaphanes celui-ci seul, à l’égard des rayons de la lumière, ne suit pas les règles ordinaires. J’ai même eu quelque nécessité de faire cette recherche, parce que les réfractions de ce cristal semblaient renverser notre explication précédente de la réfraction régulière, laquelle, au contraire, l’on verra qu’elles confirment beaucoup, après être réduites au même principe. C’est dans l’Islande qu’on trouve de gros morceaux de ce cristal, dont j’en ai vu de 4 ou 5 livres. Mais il en croît aussi en d’autres pays, car j’en ai eu de la même espèce qu’on avait trouvé en France près de la ville de Troyes en Champagne, et d’autre qui venait de l’île de Corse, quoique l’un et l’autre moins clair, et seulement en petits morceaux, à peine capables de faire remarquer quelque effet de la réfraction.

2. La première connaissance, qu’en a eu le public, est due à M. Érasme Bartholin, qui a donné la description du cristal d’Islande avec celle de ses principaux phénomènes. Mais je ne laisserai pas de donner ici la mienne, tant pour l’instruction de ceux qui n’auront pas vu son livre, que parce que dans quelques-uns de ces phénomènes il y a un peu de différence entre ses observations et celles que j’ai faites, m’étant appliqué avec beaucoup d’exactitude à examiner ces propriétés de la réfraction, afin d’en être bien sûr devant que d’entreprendre d’en éclaircir les causes.

3. Si l’on regarde à la dureté de cette pierre, et à la qualité qu’elle a de pouvoir être facilement fendue, il faut plutôt l’estimer être une espèce de talc que non pas du cristal. Car une pointe de fer l’entame aussi facilement que d’autre talc, ou que de l’albâtre, dont il égale la pesanteur.

4. Les morceaux qu’on en trouve sont de la figure d’un parallélépipède oblique, chacune des six faces étant un parallélogramme ; et il souffre d’être fendu selon toutes les trois dimensions, parallèlement à deux de ses faces opposées. Même tellement, si l’on veut, que toutes les six faces soient des rhombes égaux et semblables. La figure ici ajoutée (Fig. 19) représente un morceau de ce cristal. Les angles obtus de tous les parallélogrammes, comme ici les angles C, D, sont de 101 degrés 52 minutes, et par conséquent les aigus, comme A et B, de 78 degrés 8 minutes.

5. Des angles solides il y en a deux opposés, comme C, E, qui sont chacun composés de trois angles plans obtus et égaux. Les autres six sont composés de deux angles aigus, et d’un obtus. Tout ce que je viens de dire a été remarqué de même par M. Bartholin, dans le Traité susdit, si ce n’est que nous différons quelque peu dans la quantité des angles. Il rapporte encore quelques
Fig. 19. autres propriétés de ce cristal, savoir qu’étant frotté contre du drap, il attire des brins de paille et autres choses légères, ainsi que font l’ambre, le diamant, le verre et la cire d’Espagne ; qu’un morceau étant couvert d’eau pendant un jour ou davantage, sa surface perd son poli naturel, et que quand on y verse de l’eau forte dessus, elle fait ébullition ; surtout, à ce que j’ai trouvé, si l’on met le cristal en poudre. J’ai aussi expérimenté qu’on le peut rougir au feu, sans qu’il en soit aucunement altéré, ni rendu moins diaphane, mais qu’un feu fort violent pourtant le calcine. Sa transparence n’est guère moindre que celle de l’eau ou du cristal de roche, et sans aucune couleur. Mais les rayons de lumière y passent d’une autre façon, et produisent ces merveilleuses réfractions, dont je vais tâcher maintenant d’expliquer les causes, remettant à la fin de ce Traité de dire mes conjectures touchant la formation et la figure extraordinaire de ce cristal.

6. Dans tous les autres corps transparents que nous connaissons, il n’y a qu’une seule et simple réfraction, mais dans celui-ci il y en a deux différentes. Ce qui fait que les objets que l’on voit à travers, surtout ceux qui sont appliqués tout contre, paraissent doubles, et qu’un rayon de soleil, tombant sur une des surfaces, se partage en deux, et traverse ainsi le cristal.

7. C’est encore une loi générale dans tous les autres corps transparents, que le rayon, qui tombe perpendiculairement sur leur surface, passe tout droit sans souffrir de réfraction, et que le rayon oblique se rompt toujours. Mais dans ce cristal le rayon perpendiculaire souffre réfraction, et il y a des rayons obliques qui le passent tout droit.

8. Mais pour expliquer plus particulièrement ces phénomènes, soit derechef un morceau du même cristal A B F E (Fig. 20), et soit divisé l’angle obtus A C B, l’un des trois qui font l’angle solide équilatéral C, en deux parties égales par la droite C G, et que l’on conçoive que le cristal soit coupé par un plan qui passe par cette ligne et par le côté C F, lequel plan sera nécessairement perpendiculaire à la surface A B, et sa section dans le cristal fera un parallélogramme G C F H. Nous appellerons cette section la section principale du cristal.

Fig. 20 et 21.

9. Or si l’on couvre la surface A B (Fig. 21), en y laissant seulement une petite ouverture au point K, pris dans la droite C G, et qu’on l’expose au soleil, en sorte que ses rayons donnent dessus perpendiculairement, le rayon I K se divisera au point K en deux, dont l’un continuera d’aller droit par K L, et l’autre s’écartera par la droite K M qui est dans le plan C G H F, et qui fait avec K L un angle d’environ 6 degrés 40 minutes, tendant du côté de l’angle solide C ; et en sortant de l’autre côté du cristal, il se remettra en M Z parallèle à I K. Et comme par cette réfraction extraordinaire le point M est vu par le rayon rompu M K I, que je suppose aller à l’œil I, il faut que le point L, par cette même réfraction, soit vu par le rayon rompu L R I, en sorte que L R soit comme parallèle à M K, si la distance de l’œil K I est supposée fort grande. Le point L paraît donc comme étant dans la droite I R S, mais le même point par la réfraction ordinaire paraît aussi dans la droite I K ; donc il est nécessairement jugé double. Et de même si L est un petit trou, dans une feuille de papier ou d’autre matière qu’on aura appliquée contre le cristal, il paraîtra, en le tournant contre le jour, comme s’il y avait deux trous, qui seront d’autant plus distants l’un de l’autre que le cristal aura plus d’épaisseur.

10. Derechef, si l’on tourne le cristal en sorte qu’un rayon incident du soleil, N O, que je suppose être dans le plan continué de G C F H, fasse sur C G un angle de 73 degrés et 20 minutes et qu’il soit par conséquent presque parallèle au côté C F, qui fait sur F H un angle de 70 degrés 57 minutes, suivant le calcul que je mettrai à la fin, il se partagera en deux rayons au point O, desquels l’un continuera par O P en ligne droite avec N O, et sortira de même de l’autre côté du cristal sans se rompre aucunement, mais l’autre se rompra et ira par O Q. Et il faut noter qu’il est particulier au plan par G C F, et à ceux qui lui sont parallèles, que tous les rayons incidents qui sont dans un de ces plans, continuent d’y être après qu’ils sont entrés dans le cristal et devenus doubles ; car il en est autrement dans les rayons de tous les autres plans qui coupent le cristal, comme nous ferons voir après.

11. J’ai reconnu d’abord par ces expériences et par quelques autres, que des deux réfractions différentes que le rayon souffre dans ce cristal, il y en a une qui suit les règles ordinaires, et que c’est à elle qu’appartiennent les rayons K L et O Q. C’est pourquoi j’ai distingué cette réfraction ordinaire d’avec l’autre, et l’ayant mesurée par des observations exactes, j’ai trouvé que sa proportion, considérée dans les sinus des angles que fait le rayon incident et rompu avec la perpendiculaire, était assez précisément celle de 5 à 3, comme elle a aussi été trouvée par M. Bartholin ; et par conséquent bien plus grande que celle du cristal de roche, ou du verre, qui est à peu près de 3 à 2.

12. La manière de faire exactement ces observations est telle. Il faut tracer sur un papier, attaché sur une table bien unie, une ligne noire A B (Fig. 22), et deux autres qui la coupent à angles droits C E D, K M L, plus ou moins distante l’une de l’autre selon qu’on veut examiner un rayon plus ou moins oblique, et poser le cristal sur l’intersection E, en sorte que la ligne A B convienne à celle qui divise également l’angle obtus de la surface d’en bas, ou à quelque ligne parallèle. Alors en plaçant l’œil directement au-dessus de la ligne A B
Fig. 22., elle ne paraîtra que simple, et l’on verra que sa partie vue à travers le cristal, avec les parties qui paraissent au dehors, se rencontreront en ligne droite ; mais la ligne C D paraîtra double, et l’on distinguera l’image qui vient de la réfraction régulière, de ce qu’elle paraît plus élevée que l’autre lorsqu’on regarde avec les deux yeux, ou bien de ce qu’en tournant le cristal sur le papier, elle demeure ferme, au lieu que l’autre image remue et tourne tout autour.

L’on placera ensuite l’œil en I (demeurant toujours dans le plan perpendiculaire par A B), en sorte qu’il voie l’image de la ligne C D, qui vient de la réfraction régulière, faire une ligne droite avec le reste de cette ligne, qui est dehors le cristal. Et marquant alors sur la surface du cristal le point H, où parait l’intersection E, ce point sera directement au-dessus de E. Puis on retirera l’œil vers O, toujours dans le plan perpendiculaire par A B, en sorte que l’image de la ligne C D, qui se fait par la réfraction ordinaire, paraisse en ligne droite avec la ligne K L vue sans réfraction ; et l’on marquera sur le cristal le point N, où paraît le point d’intersection E.

13. L’on connaîtra donc la longueur et la position des lignes N H, E M et H E, qui est l’épaisseur du cristal ; lesquelles lignes étant tracées à part sur un plan, et joignant alors N E et N M qui coupe H E en P, la proportion de la réfraction sera celle de E N à N P, parce que ces lignes sont entre elles comme les sinus des angles N P H, N E P, qui sont égaux à ceux que le rayon incident O N et sa réfraction N E font avec la perpendiculaire à la surface. Cette proportion, comme j’ai dit, est assez précisément comme de 5 à 3, et toujours la même dans toutes les inclinaisons du rayon incident.

14. La même manière d’observer m’a aussi servi à examiner la réfraction extraordinaire ou irrégulière de ce cristal. Car le point H étant trouvé, et marqué, comme il a été dit, directement au-dessus du point E, j’ai regardé l’apparence de la ligne C D, qui se fait par la réfraction extraordinaire ; et ayant placé l’œil en Q (Fig. 23) en sorte, que cette apparence fît une ligne droite avec la ligne K L vue
Fig. 23. sans réfraction, j’ai connu les triangles R E H, R E S, et partant les angles R S H, R E S, que le rayon incident et le rompu font avec la perpendiculaire.

15. Mais j’ai trouvé dans cette réfraction, que la raison de E R à R S n’était pas constante, comme dans la réfraction ordinaire, mais qu’elle variait suivant la différente inclinaison du rayon incident.

16. Je trouvai aussi, que quand Q R E faisait une ligne droite, c’est-à-dire que le rayon incident entrait dans le cristal sans se rompre (ce que je reconnus de ce que alors le point E, vu par la réfraction extraordinaire, paraissait dans la ligne C D vue sans réfraction), je trouvai, dis-je, alors que l’angle Q R G était de 73 degrés 20 minutes, comme il a été déjà remarqué, et qu’ainsi ce n’est pas le rayon parallèle au côté du cristal, qui le traverse en droite ligne sans se rompre, comme a cru M. Bartholin, puisque son inclinaison n’est que de 70 degrés 57 minutes, comme il a été dit
Fig. 24. ci-dessus, ce qui est à noter, afin qu’on ne cherche pas en vain la cause de la propriété singulière de ce rayon, dans son parallélisme aux dits côtés.

17. Enfin, continuant mes observations pour découvrir la nature de cette réfraction, j’appris qu’elle gardait cette règle remarquable qui s’ensuit. Soit tracé à part le parallélogramme G C F H (Fig. 24), fait par la section principale du cristal ci-devant déterminée. Je trouvai donc que toujours, quand les inclinaisons de deux rayons qui viennent de côtés opposés, comme ici V K, S K, sont égales, leurs réfractions K X et K T rencontrent la droite du fond H F en sorte, que les points X et T sont également distants du point M, où tombe la réfraction du rayon perpendiculaire I K, ce qui a aussi lieu dans les réfractions des autres sections de ce cristal. Mais devant que de parler de celles-là, qui ont encore d’autres propriétés particulières, nous rechercherons les causes des phénomènes que j’ai déjà rapportés.

Ce fut après avoir expliqué la réfraction des corps transparents ordinaires, par le moyen des émanations sphériques de la lumière, ainsi que dessus, que je repris l’examen de la nature de ce cristal, où je n’avais rien pu découvrir auparavant.

18. Comme il y avait deux réfractions différentes, je conçus qu’il y avait aussi deux différentes émanations d’ondes de lumière, et que l’une se pouvait faire dans la matière éthérée répandue dans le corps du cristal. Laquelle matière étant en beaucoup plus grande quantité que n’est celle des particules qui le composent, était seule capable de causer la transparence, suivant ce qui a été expliqué ci-devant. J’attribuai à cette émanation d’ondes la réfraction régulière qu’on observe dans cette pierre, en supposant ces ondes de forme sphérique à l’ordinaire, et d’une extension plus lente au dedans du cristal qu’elles ne sont au dehors ; d’où j’ai fait voir que procède la réfraction.

19. Quant à l’autre émanation qui devait produire la réfraction irrégulière, je voulus essayer ce que feraient des ondes elliptiques, ou pour mieux dire sphéroïdes ; lesquelles je supposai qu’elles s’étendaient indifféremment, tant dans la matière éthérée répandue dans le cristal, que dans les particules dont il est composé, suivant la dernière manière dont j’ai expliqué la transparence. Il me semblait que la disposition, ou arrangement régulier de ces particules, pouvait contribuer à former les ondes sphéroïdes (n’étant requis pour cela sinon que le mouvement successif de la lumière s’étendît un peu plus vite en un sens qu’en l’autre), et je ne doutai presque point qu’il n’y eût dans ce cristal un tel arrangement de particules égales et semblables, à cause de sa figure et de ses angles d’une mesure certaine et invariable. Touchant lesquelles particules, et leur forme et disposition, je proposerai sur la fin de ce Traité mes conjectures, et quelques expériences qui les confirment.

20. La double émanation d’ondes de lumière, que je m’étais imaginée, me devint plus probable après certain phénomène que j’observai dans le cristal ordinaire qui croît en forme hexagone, et qui, à cause de cette régularité, semble aussi être composé de particules de certaine figure et rangées avec ordre. C’était que ce cristal a une double réfraction, aussi bien que celui d’Islande, quoique moins évidente. Car en ayant fait tailler des prismes bien polis, par des sections différentes, je remarquai dans tous, en regardant la flamme de la chandelle à travers, ou le plomb des vitres qui sont aux fenêtres, que tout paraissait double, quoique avec des images peu distantes entre elles. D’où je compris la raison pourquoi ce corps si transparent est inutile aux lunettes d’approche, quand elles ont tant soit peu de longueur.

21. Or cette double réfraction, suivant ma théorie ci-dessus établie, semblait demander une double émanation d’ondes de lumière, toutes deux sphériques (car les deux réfractions sont régulières) et les unes seulement un peu plus lentes que les autres. Car par là ce phénomène s’explique fort naturellement, en supposant les matières qui servent de véhicules à ces ondes, de même que j’ai fait dans le cristal d’Islande. J’eus donc moins de peine après cela à admettre deux émanations d’ondes dans un même corps. Et pour ce que l’on pouvait m’objecter qu’en composant ces deux cristaux de particules égales de certaine figure, et entassées régulièrement, à peine les interstices que ces particules laissent et qui contiennent de la matière éthérée suffiraient pour transmettre les ondes de lumière que j’y ai placées, j’ôtai cette difficulté en considérant ces particules comme étant d’un tissu fort rare, ou bien composées d’autres particules beaucoup plus petites, entre lesquelles la matière éthérée passe fort librement. Ce qui d’ailleurs s’ensuit nécessairement de ce qui a été démontré ci-devant, touchant le peu de matière dont les corps sont assemblés.

22. Supposant donc ces ondes sphéroïdes outre les sphériques, je commençai à examiner si elles pouvaient servir à expliquer les phénomènes de la réfraction irrégulière, et comment par ces phénomènes mêmes je pourrais déterminer la figure et la position des sphéroïdes : en quoi, j’obtins à la fin le succès désiré, en procédant comme s’ensuit.

23. Je considérai premièrement l’effet des ondes ainsi formées, à l’égard du rayon qui tombe perpendiculairement sur la surface plate d’un corps transparent, dans lequel elles s’étendraient de cette manière. Je posai A B (Fig. 25) pour l’endroit découvert de la surface. Et puisqu’un rayon perpendiculaire sur un plan, et venant d’une lumière fort
Fig. 25. distante, n’est autre chose, par la théorie précédente, que l’incidence d’une parcelle d’onde parallèle à ce plan, je supposai la droite R C, parallèle et égale à A B, être une portion d’onde de lumière, dont les points infinis R H h C viennent rencontrer la surface A B aux points A K k B. Donc au lieu des ondes particulières hémisphériques, qui dans un corps de réfraction ordinaire se devaient étendre de chacun de ces derniers points, ainsi que nous avons expliqué ci-dessus en traitant de la réfraction, ce devaient être ici des hémisphéroïdes, desquels je supposai que les axes ou bien les grands diamètres étaient obliques au plan A B, ainsi que l’est A V, demi-axe ou demi-grand diamètre du sphéroïde S V T, qui représente l’onde particulière venant du point A, après que l’onde R C est venue en A B. Je dis ou axe ou grand diamètre, parce que la même ellipse S V T peut être considérée comme section d’un sphéroïde dont l’axe est A Z, perpendiculaire à A V. Mais pour le présent, sans déterminer encore l’un ou l’autre, nous considérerons ces sphéroïdes seulement dans leurs sections qui font les ellipses dans le plan de cette figure. Or prenant un certain espace de temps pendant lequel du point A s’est étendue l’onde S V T, il fallait que de tous les autres points K k B il se fît, dans le même temps, des ondes pareilles et semblablement posées que S V T. Et la commune tangente N Q de toutes ces demi-ellipses, était la propagation de l’onde R C dans le corps transparent proposé par la théorie de ci-dessus. Parce que cette ligne est celle qui termine, dans un même instant, le mouvement qui a été causé par l’onde R C en tombant sur A B, et où ce mouvement se trouve en beaucoup plus grande quantité que partout ailleurs, comme étant faite des arcs infinis d’ellipses, dont les centres sont le long de la ligne A B.

24. Or il paraissait que cette tangente commune N Q était parallèle à A B, et de même longueur, mais qu’elle ne lui était pas opposée directement, puisqu’elle était comprise des lignes A N, B Q, qui sont des diamètres conjugués des ellipses qui ont A et B pour centres, à l’égard des diamètres qui sont dans la droite A B. Et c’est ainsi que j’ai compris, ce qui m’avait paru fort difficile, comment un rayon perpendiculaire à une surface pouvait souffrir réfraction en entrant dans le corps transparent, voyant que l’onde R C, étant venue à l’ouverture A B, continuait de là en avant à s’étendre entre les parallèles A N, B Q, demeurant pourtant elle-même toujours parallèle à A B, de sorte qu’ici la lumière ne s’étend pas par des lignes perpendiculaires à ses ondes, comme dans la réfraction ordinaire, mais ces lignes coupent les ondes obliquement.

Fig. 26.

25. Cherchant ensuite quelle pouvait être la situation, et forme de ces sphéroïdes dans le cristal, je considérai que toutes les six faces produisaient précisément les mêmes réfractions. Reprenant donc le parallélépipède A F B (Fig. 26), dont l’angle solide obtus, compris de trois angles plans égaux, est C, et y concevant les trois sections principales, dont l’une est perpendiculaire à la face D C, et passe par le côté C F, l’autre perpendiculaire à la face B F passant par le côté C A, et la troisième perpendiculaire à la face A F passant par le côté B C, je savais que les réfractions des rayons incidents, appartenant à ces trois plans, étaient toutes pareilles. Mais il ne pouvait y avoir de position de sphéroïde qui eut un même rapport à ces trois sections, sinon de celui dont l’axe fût aussi l’axe de l’angle solide C. Partant je vis que l’axe de cet angle, c’est-à-dire la droite qui du point C traversait le cristal avec inclinaison égale aux côtés C F, C A, C B, était la ligne qui déterminait la position des axes de toutes les ondes sphéroïdes qu’on s’imaginait naître de quelque point, pris au dedans ou à la surface du cristal, puisque tous ces sphéroïdes devaient être semblables, et avoir leurs axes parallèles entre eux.

Fig. 27.

26. Considérant après cela le plan de l’une de ces trois sections, savoir de celle par G C F, dont l’angle C est de 109 degrés 3 minutes, puisque l’angle F était ci-dessus de 70 degrés 57 minutes, et imaginant une onde sphéroïde autour du centre C, je savais, par ce que je viens d’expliquer, que son axe devait être dans ce même plan, duquel axe je marquai la moitié par C S dans cette autre figure (Fig. 27), et cherchant paf le calcul (qui sera rapporté avec les autres à la fin de ce discours) l’angle G C S, je le trouvai de 45 degrés 20 minutes.

27. Pour connaître après cela la forme de ce sphéroïde, c’est-à-dire la proportion des demi-diamètres C S, C P, de sa section elliptique, qui sont l’un à l’autre perpendiculaires, je considérai que le point M, où l’ellipse est touchée par la droite F H, parallèle à C G, devait être tellement situé, que C M avec la perpendiculaire C L fît un angle de 6 degrés 40 minutes. Parce que, cela étant, cette ellipse satisfaisait à ce qui a été dit de la réfraction du rayon perpendiculaire à la surface C G, lequel s’écarte de la perpendiculaire C L par ce même angle. Ce qui étant donc ainsi posé, et faisant C M de 100 000 parties, je trouvai par le calcul, qui sera mis à la fin, le demi-grand diamètre C P de 105 032, et le demi-axe C S de 93 410, dont la raison est fort près comme de 9 à 8, de sorte que le sphéroïde était de ceux qui ressemblent à une sphère comprimée, étant produit par la circulation d’une ellipse à l’entour de son petit diamètre. Je trouvai aussi C G, demi-diamètre parallèle à la tangente M L, de 98 779.

28. Or passant à la recherche des réfractions que les rayons incidents obliques devaient faire, suivant l’hypothèse de ces ondes sphéroïdes, je vis que ces réfractions dépendaient de la proportion de la vitesse qui est entre le mouvement de la lumière hors du cristal dans l’éther, et le mouvement au dedans du même. Car supposant par exemple que cette proportion fût telle que, pendant que la lumière dans le cristal fait le sphéroïde G S P, tel que je viens de dire, elle fasse au dehors une sphère dont le demi-diamètre soit égal à la ligne N, laquelle sera déterminée ci-après, voici la manière de trouver la réfraction des rayons incidents. Soit un tel rayon R C, qui tombe sur la surface C K (Fig. 28). Il faut faire C O perpendiculaire à R C, et dans l’angle K C O ajuster O K, qui soit égal à N, et perpendiculaire à C O ; puis mener K I qui touche l’ellipse G S P, et du point de contact I joindre I C,
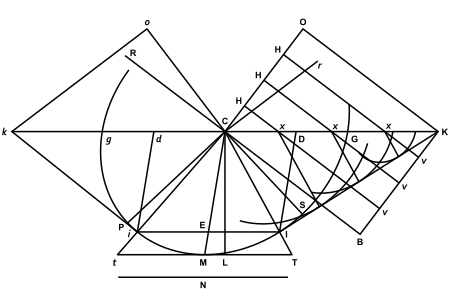
Fig. 28 qui sera la réfraction requise du rayon R C. Dont on verra que la démonstration est tout à fait semblable à celle dont nous nous sommes servis en expliquant la réfraction ordinaire. Car la réfraction du rayon R C n’est autre chose que le progrès de l’endroit C de l’onde C O, continuée dans le cristal. Or les endroits H de cette onde, pendant le temps que O est venu en K, seront arrivés à la surface C K par les droites H x, et auront de plus produit, dans le cristal, des ondes particulières hémisphéroïdes des centres x, semblables et semblablement posées avec l’hémisphéroïde G S P g, et dont les grands et les petits diamètres auront même raison aux lignes x v (continuation des H x jusqu’à K B, parallèle à C O) que les diamètres du sphéroïde G S P ont à la ligne C B, ou N. Et il est bien aisé de voir que la commune tangente de tous ces sphéroïdes, qui sont ici représentés par des ellipses, sera la droite I K, qui pour cela sera la propagation de l’onde C O, et le point I celle du point C, conformément à ce qui a été démontré dans la réfraction ordinaire.

Pour ce qui est de l’invention du point de contact I, l’on sait qu’il faut trouver aux lignes C K, C G, la troisième proportionnelle C D, et tirer D I parallèle à C M, déterminée ci-devant, qui est le diamètre conjugué à C G, car alors, en menant K I, elle touche l’ellipse en I.

29. Or de même que nous avons trouvé C I la réfraction du rayon R C, l’on trouvera aussi C i celle du rayon r C, qui vient du côté opposé, en faisant C o perpendiculaire à r C, et poursuivant le reste de la construction ainsi qu’auparavant.

Où l’on voit que si le rayon r C est également incliné avec R C, la ligne C d sera nécessairement égale à C D, parce que C k est égale à C K, et C g à C G. Et que par conséquent I i sera coupée en E en parties égales par la ligne C M, à laquelle D I, d i sont parallèles. Et parce que C M est le diamètre conjugué à C G, il s’ensuit que i I sera parallèle à g G. Partant si on prolonge les réfractions C I, C i, jusqu’à ce qu’elles rencontrent la tangente M L en T et t, les distances M T, M t, seront aussi égales. Et ainsi s’explique parfaitement, par notre hypothèse, le phénomène ci-dessus rapporté, savoir que quand il y a deux rayons également inclinés, mais venant de côtés opposés, comme ici les rayons R C, r C, leurs réfractions s’écartent également de la ligne que suit la réfraction du rayon perpendiculaire, en considérant ces écarts dans la parallèle à la surface du cristal.

30. Pour trouver la longueur de la ligne N, à proportion des C P, C S, C G, c’est par les observations de la réfraction irrégulière qui se fait dans cette section du cristal, qu’elle se doit déterminer, et je trouve par là que la raison de N à G C est tant soit peu moindre que de 8 à 5. Et ayant encore égard à d’autres observations et phénomènes, dont il sera parlé après, je mets N de 156 962 parties, desquelles le demi-diamètre C G est trouvé en contenir 98 779, ce qui fait cette raison de 8 à 5 1/29. Or cette proportion, qui est entre la ligne N et C G, se peut appeler la proportion de la réfraction, de même que dans le verre celle de 3 à 2, comme il sera manifeste après que j’aurai expliqué ici un abrégé de la manière précédente pour trouver les réfractions irrégulières.

31. Supposé donc, dans cette autre figure (Fig. 29), comme auparavant, la surface du cristal g G, l’ellipse G P g, et la ligne N ; et C M la réfraction du rayon perpendiculaire F C, duquel elle s’écarte de 6 degrés 40 minutes, soit maintenant quelqu’autre rayon R C, dont il faille trouver la réfraction.

Du centre C, avec le demi-diamètre C G, soit décrite la circonférence g R G, coupant le rayon R C en R, et soit R V perpendiculaire sur C G. Puis toujours, comme la ligne N à C G, ainsi soit C V à C D, et soit menée D I parallèle à C M, coupant l’ellipse g M G en I ; alors joignant C I, ce sera la réfraction requise du rayon R C. Ce qui se démontre ainsi.

Fig. 29

Soit C O perpendiculaire à C R, et dans l’angle O C G soit ajustée O K égale à N et perpendiculaire à C O, et menée la droite K I, laquelle si elle est démontrée touchante de l’ellipse en I, il sera évident, par les choses ci-devant expliquées, que C I est la réfraction du rayon R C. Or puisque l’angle R C O est droit, il est aisé de voir que les triangles rectangles R C V, K C O sont semblables. Comme donc C K à K O, ainsi R C à C V. Mais K O est égale à N et R C à C G : donc comme C K à N, ainsi sera C G à C V. Mais comme N à C G, ainsi est, par la construction, C V à C D : donc comme C K à C G, ainsi C G à C D. Et parce que D I est parallèle à C M, diamètre conjugué de C G, il s’ensuit que K I touche l’ellipse en I, ce qui restait à démontrer.

32. L’on voit donc que comme il y a, dans la réfraction des diaphanes ordinaires, une certaine proportion constante entre les sinus des angles que font le rayon incident, et rompu, avec la perpendiculaire, il y a ici une telle proportion entre C V et C D, ou I E, c’est-à-dire, entre le sinus de l’angle que fait le rayon incident avec la perpendiculaire, et l’appliquée dans l’ellipse, interceptée entre la réfraction de ce rayon, et le diamètre C M. Car la raison de C V à C D, comme il a été dit, est toujours la même que de N au demi-diamètre C G.

33. J’ajouterai ici, devant que de passer outre, qu’en comparant ensemble la réfraction régulière et irrégulière de ce cristal, il y a cela de remarquable que, si A B P S (Fig. 30) est le sphéroïde par lequel s’étend la lumière dans le cristal dans un certain espace de temps, laquelle extension, comme il a été dit, sert à la réfraction irrégulière, alors la sphère inscrite B V S T est l’étendue, dans ce même espace de temps, de la lumière qui sert à la réfraction régulière.

Car nous avons dit ci-devant que, la ligne N étant le rayon d’une onde sphérique de lumière dans l’air, pendant que dans le cristal elle s’étendait par le sphéroïde A B P S, la raison de N à C S était de 156 962 à 93 410. Mais il a aussi été dit que la proportion de la réfraction régulière était de 5 à 3, c’est-à-dire que, N étant le rayon d’une onde sphérique de lumière dans l’air, son extension dans le cristal faisait, en même espace de temps, une sphère dont le rayon était à N comme 3 à 5. Or
Fig. 30. 156 962 est à 93 410 comme 5 à 3 moins 1/41. De sorte que c’est assez près, et peut-être exactement, la sphère B V S T que fait la lumière pour la réfraction régulière dans le cristal, pendant qu’elle y fait le sphéroïde B P S A pour la réfraction irrégulière, et pendant qu’elle fait la sphère au rayon N en l’air, hors du cristal.

Quoiqu’il y ait donc, selon ce que nous avons posé, deux différentes extensions de la lumière dans ce cristal, il paraît que c’est seulement dans le sens des perpendiculaires à l’axe B S du sphéroïde, que l’une des extensions est plus vite que l’autre, mais qu’elles sont d’égale vitesse en l’autre sens, savoir en celui des parallèles au même axe B S, qui est aussi l’axe de l’angle obtus du cristal.

34. Je montrerai maintenant que, la proportion de la réfraction étant telle que l’on vient de voir, il faut qu’il s’ensuive de là cette propriété notable du rayon qui, tombant obliquement sur la surface du cristal, le passe sans souffrir de réfraction. Car supposant les même choses que devant, et que le rayon R C (Fig. 31) fasse sur la surface g G

Fig. 31 et 32. l’angle R C G de 73 degrés 20 minutes penchant du même côté que le cristal, duquel rayon il a été parlé dessus, si l’on cherche, par la manière ci-devant expliquée, sa réfraction C I, l’on trouvera qu’elle fait justement une droite avec R C, et qu’ainsi ce rayon ne se détourne point du tout, conformément à l’expérience. Ce qui se prouve ainsi par le calcul.

C G ou C R étant, comme dessus, 98 779, C M 100 000 et l’angle R C V de 73 degrés 20 minutes, C V sera 28 330. Mais parce que C I est la réfraction du rayon R C, la proportion de C V à C D est celle de 156 962 à 98 779, savoir de N à CG : donc C D est 17 828. Or comme le carré de C G au carré de C M, ainsi le rectangle g D G au carré D I : donc D I ou C E sera 98 353. Mais comme C E à E I, ainsi C M à M T, qui sera donc 18 127. Et étant ajoutée à M L, qui est 11 609 (savoir le sinus de l’angle L C M de 6 degrés 40 minutes, en supposant C M 100 000 pour rayon) vient L T 27 936, qui est à L C 99 324, comme C V à V R, c’est-à-dire comme 29 938, tangente du complément de l’angle R C V de 73 degrés 20 minutes au rayon des Tables. D’où il paraît que R C I T (Fig. 32) est une ligne droite : ce qu’il fallait prouver.

35. L’on verra de plus que le rayon C I, en sortant par la surface opposée du cristal, doit encore passer tout droit, par la démonstration suivante, qui prouve que la réciprocation des réfractions s’observe dans ce cristal de même que dans les autres corps diaphanes, c’est-à-dire que si un rayon R C, en rencontrant la surface du cristal C G, se rompt en C I, le rayon C I, sortant par la surface opposée et parallèle du cristal, que je suppose être I B, aura sa réfraction I A parallèle au rayon R C.

Fig. 33.

Soient posées les mêmes choses qu’auparavant, c’est-à-dire que C O, perpendiculaire à C R (Fig. 33), représente une portion d’onde, dont la continuation dans le cristal soit I K, de sorte que l’endroit C se sera continué par la droite C I, pendant que O est venu en K. Que si l’on prend maintenant un second temps égal au premier, l’endroit K de l’onde I K, dans ce second temps, sera avancé par la droite K B, et parallèle à C I, parce que tout endroit de l’onde C O, en arrivant à la surface C K, doit continuer dans le cristal de même que l’endroit C ; et dans ce même temps il se fera du point I, dans l’air, une onde sphérique particulière ayant le demi-diamètre I A égal à K O, puisque K O a été parcourue dans un temps égal. De même si l’on considère
Fig. 34. quelqu’autre point de l’onde I K, comme h (Fig. 34), il ira par h m, parallèle à C I, rencontrer la surface I B, pendant que le point K parcourt K l égal à h m ; et pendant que celui-ci achève le reste l B, il se sera fait du point m une onde particulière, dont le demi-diamètre m n, aura telle raison à l B que I A à K B. D’où il est évident que cette onde du demi-diamètre m n, et l’autre du demi-diamètre I A, auront la même tangente B A. Et de même toutes les ondes particulières sphériques qui se seront faites hors du cristal par l’impulsion de tous les points de l’onde I K contre la surface de l’éther I B. C’est donc précisément la tangente B A qui sera, hors du cristal, la continuation de l’onde I K, lorsque l’endroit K est venu en B. Et par conséquent I A, qui est perpendiculaire à B A, sera la réfraction du rayon C I, en sortant du cristal. Or il est clair que I A est parallèle au rayon incident R C, puisque I B est égale à C K, et I A égale à K O, et les angles A et O droits.

L’on voit donc que, suivant notre hypothèse, la réciprocation des réfractions a lieu dans ce cristal, aussi bien que dans les corps transparents ordinaires, ce qui se trouve ainsi en effet par les observations.

36. Je passe maintenant à la considération des autres sections du cristal, et des réfractions qui s’y produisent, desquelles, comme l’on verra, dépendent d’autres phénomènes fort remarquables.

Soit le parallélépipède du cristal A B H (Fig. 35), et la surface d’en haut A E H F un rhombe parfait, dont les angles obtus soient divisés également par la droite E F, et les angles aigus par la droite A H, perpendiculaire à F E.

La section, que nous avons considérée jusqu’ici, est celle qui passe par les lignes E F, E B, et qui,
Fig. 35. en même temps, coupe le plan A E H F à angles droits ; de laquelle les réfractions ont cela de commun avec les réfractions des diaphanes ordinaires, que le plan qui est mené par le rayon
Fig. 36. incident, et qui coupe à angles droits la surface du cristal, est celui dans lequel se trouve aussi le rayon rompu. Mais les réfractions qui appartiennent à toute autre section de ce cristal, ont cette étrange propriété, que le rayon rompu sort toujours du plan du rayon incident, perpendiculaire à la surface, et se détourne du côté du penchant du cristal. De quoi nous ferons voir la raison premièrement dans la section par A H, et nous montrerons en même temps, comment on y peut déterminer les réfractions suivant notre hypothèse. Soit donc dans le plan qui passe par A H et qui est perpendiculaire au plan A F H E (Fig. 36), le rayon incident R C, et qu’il faille trouver la réfraction dans le cristal.

37. Du centre C, que je suppose être dans l’intersection de A H et F E, soit imaginé un demi-sphéroïde Q G q g M, tel que doit faire la lumière en s’étendant dans le cristal, et que sa section, par le plan A E H F, fasse l’ellipse Q G q g, dont le grand diamètre Q q, qui est dans la ligne A H, sera nécessairement un des grands diamètres du sphéroïde ; parce que l’axe du sphéroïde étant dans le plan par F E B, auquel Q C est perpendiculaire, il s’ensuit que Q C est aussi perpendiculaire à l’axe du sphéroïde, et partant Q C q un de ses grands diamètres. Mais le petit diamètre de cette ellipse, G g, aura à Q q la raison qui a été définie ci-devant, n^o 27, entre C G et le demi-grand diamètre du sphéroïde C P, savoir celle de 98 779 à 105 032.

Soit la longueur de la ligne N le trajet de la lumière dans l’air, pendant que dans le cristal, du centre C, elle fait le sphéroïde Q G q g M, et ayant mené C O perpendiculaire au rayon C R, et qui soit dans le plan par C R et A H, soit ajustée, dans l’angle A C O, la droite O K égale à N, et perpendiculaire à C O, et qu’elle rencontre la droite A H en K. Posant ensuite que C L soit perpendiculaire à la surface du cristal A E H F, et que C M soit la réfraction du rayon qui tombe perpendiculairement sur cette même surface, soit mené un plan par la ligne C M et par K C H, faisant dans le sphéroïde la demi-ellipse Q M q, qui sera donnée, puisque l’angle M C L est donné de 6 degrés 40 minutes. Et il est certain, suivant ce qui a été expliqué ci-dessus, n^o 27, qu’un plan qui toucherait le sphéroïde au point M, où je suppose que la droite C M rencontre sa surface, serait parallèle au plan Q G q. Si donc par le point K l’on tire maintenant K S parallèle à G g, qui sera aussi parallèle à Q X, tangente de l’ellipse Q G q en Q, et que l’on conçoive un plan passant par K S, et qui touche le sphéroïde, le point de contact sera nécessairement dans l’ellipse Q M q, parce que ce plan par K S, aussi bien que le plan qui touche le sphéroïde au point M, sont parallèles à Q X tangente du sphéroïde : car cette conséquence sera démontrée à la fin de ce Traité. Que ce point de contact soit en I, faisant proportionnelles K C, Q C, D C, et menant D I parallèle à C M, et qu’on joigne C I. Je dis que C I sera la réfraction requise du rayon R C. Ce qui sera manifeste si, en considérant C O, qui est perpendiculaire au rayon R C, comme une portion d’onde de lumière, nous démontrons que la continuation de son endroit C se trouve dans le cristal en I, lorsque O est arrivé en K.

38. Or comme en démontrant, au chapitre de la réflexion, que le rayon incident et réfléchi étaient toujours dans un même plan perpendiculaire à la surface réfléchissante, nous avons considéré la largeur de l’onde de lumière ; de même il faut considérer ici la largeur de l’onde C O dans le diamètre C g. Prenant donc la largeur C c du côté de l’angle E, soit pris le rectangle C O o c comme une portion d’onde, et achevons les rectangles C K k c, C I i c, K I i k, O K k o. Dans le temps donc que la ligne O o est arrivée à la surface du cristal en K k, tous les points de l’onde C O o c sont arrivés au rectangle K c par des lignes parallèles à O K, et des points de leurs incidences il s’est, outre cela, fait des demi-sphéroïdes particuliers dans le cristal, semblables et semblablement posés au demi-sphéroïde Q M q, lesquels vont nécessairement tous toucher au plan du parallélogramme K I i k, au même instant que O o est en K k. Ce qui est aisé à comprendre, puisque tous ceux de ces demi-sphéroïdes, qui ont leur centre le long de la ligne C K, touchent à ce plan dans la ligne K I, (car cela se démontre de la même façon que nous avons démontré la réfraction du rayon oblique dans la section principale par E F) et que tous ceux, qui ont leur centre dans la ligne C c, touchent le même plan K i dans la ligne I i, étant tous ceux-ci pareils au demi-sphéroïde Q M q. Puisque donc le parallélogramme K i est celui qui touche tous ces sphéroïdes, ce même parallélogramme sera précisément la continuation de l’onde C O o c dans le cristal, lorsque O o est parvenue en K k, à cause de la terminaison du mouvement, et de la quantité qui s’y en trouve plus que partout ailleurs : et ainsi il paraît que l’endroit C de l’onde C O o c a sa continuation en I, c’est-à-dire que le rayon R C se rompt en C I.

Où il est à noter, que la proportion de la réfraction pour cette section du cristal est celle de la ligne N au demi-diamètre C Q, par laquelle on trouvera facilement les réfractions de tous les rayons incidents, de la même manière que nous avons montré ci-devant ce qui est de la section par F E, et la démonstration sera la même. Mais il paraît que ladite proportion de la réfraction est moindre ici que dans la section par F E B, car elle était là comme de N à C G, c’est-à-dire de 156 962 à 98 779, fort près comme de 8 à 5, et ici elle est de N à C Q, demi-grand diamètre du sphéroïde, c’est-à-dire de 156 962 à 105 032, fort près comme de 3 à 2, mais tant soit peu moindre. Ce qui s’accorde encore parfaitement à ce que l’on trouve par observation.

39. Au reste cette diversité de proportions de réfraction produit un effet fort singulier dans ce cristal, qui est qu’en le posant sur un papier, où il y ait des lettres ou autre chose marquée, si on regarde dessus, avec les deux yeux situés dans le plan de la section par E F, on voit les lettres plus élevées par cette réfraction irrégulière, que lorsqu’on met les yeux dans le plan de la section par A H ; et la différence des élévations paraît par l’autre réfraction ordinaire de ce cristal, dont la proportion est comme de 5 à 3, et qui élève ces lettres toujours également, et plus haut que ne fait la réfraction irrégulière. Car on voit les lettres, et le papier où elles sont écrites, comme dans deux étages différents tout à la fois ; et dans la première situation des yeux, savoir quand ils sont dans le plan par A H, ces deux étages sont quatre fois plus éloignés l’un de l’autre que lorsque les yeux sont dans le plan par E F.

Nous montrerons que cet effet s’ensuit de ces réfractions, ce qui servira en même temps à faire connaître le lieu apparent d’un point d’objet, placé immédiatement sous le cristal, suivant la différente situation des yeux.

40. Voyons premièrement de combien la réfraction irrégulière du plan par A H doit hausser le fond du cristal. Que le plan de cette figure ici (Fig. 37)
Fig. 37. représente séparément la section par Q q et C L, dans laquelle section est aussi le rayon R C, et que le plan demi-elliptique, par Q q et C M, soit incliné au premier, comme auparavant, d’un angle de 6 degrés 40 minutes, dans lequel plan est donc C I la réfraction du rayon R C.

Que si l’on considère maintenant le point I comme au fond du cristal, et qu’il soit vu par les rayons I C R, I c r, rompus également aux points C c, qui doivent être également distants de D, et que ces rayons rencontrent les deux yeux en R r. Il est certain que le point I paraîtra élevé en S, où concourent les droites R C, r c, lequel point S est dans D P, perpendiculaire à Q q. Et si sur D P on mène la perpendiculaire I P, qui sera toute couchée au fond du cristal, la longueur S P sera l’exhaussement apparent du point I au-dessus de ce fond.

Soit décrit sur Q q un demi-cercle qui coupe le rayon C R en B, d’où soit menée B V perpendiculaire à Q q, et que la proportion de la réfraction pour cette section soit, comme devant, celle de la ligne N au demi-diamètre C Q.

Donc, comme N à C Q, ainsi est V C à C D, comme il paraît par la manière de trouver les réfractions que nous avons montrée ci-dessus n^o 31, mais comme V C à C D, ainsi V B à D S. Donc comme N à C Q, ainsi V B à D S. Soit M L perpendiculaire sur C L. Et parce que je suppose les yeux R r éloignés du cristal d’un pied ou environ, et par conséquent l’angle R S r fort petit, il faut considérer V B comme égale au demi-diamètre C Q, et D P comme égale à C L : donc comme N à C Q, ainsi C Q à D S. Mais N est de 156 962 parties, dont C M en contient 100 000 et C Q 105 032 : donc D S sera de 70 283. Mais C L est de 99 324, étant sinus du complément de l’angle M C L de 6 degrés 40 minutes, en supposant C M pour rayon : donc D P, considérée comme égale à C L, sera à D S comme 99 324 à 70 283. Et ainsi se connaît le rehaussement du point du fond I par la réfraction de cette section.

Fig. 38.

41. Soit maintenant représentée l’autre section par E F dans la figure qui est devant la précédente (Fig. 36), et que G M g soit la demi-ellipse, considérée aux n^os 27 et 28, qui se fait par la coupe d’une onde sphéroïde ayant le centre C. Que le point I, pris dans cette ellipse, soit imaginé derechef au fond du cristal, et qu’il soit vu par les rayons rompus I C R, I c r (Fig. 38), qui vont rencontrer les deux yeux, étant C R, c r également inclinées à la surface du cristal G g. Ce qui étant ainsi, si l’on tire I D parallèle à C M, que je suppose être la réfraction du rayon perpendiculaire qui tomberait sur le point C, les distances D C, D c seront égales, comme il est aisé de voir par ce qui est démontré au nombre 28. Or il est certain que le point I doit paraître en S, où concourent les droites R C, r c, prolongées, et que ce point S tombe dans la ligne D P perpendiculaire à G g, à laquelle D P si
Fig. 39. l’on mène perpendiculaire I P, ce sera la distance P S qui marquera le rehaussement apparent du point I. Soit sur G g décrit un demi-cercle qui coupe C R en B, d’où soit menée B V perpendiculaire sur G g, et que N à G C marque la proportion de la réfraction dans cette section, comme au n^o 28. Puisque donc C I est la réfraction du rayon B C, et D I parallèle à C M, il faut que V C soit à C D, comme N à G C, par ce qui a été démontré au nombre 31, mais comme V C à C D, ainsi est B V à D S. Soit menée M L perpendiculaire sur C L. Et parce que je suppose derechef les yeux éloignés au-dessus du cristal, B V est censée égale au demi-diamètre C G, et partant D S sera alors troisième proportionnelle aux lignes N et C G : aussi sera D P alors censée égale à C L. Or C G étant de 98 778 parties dont C M en contient 100 000, N est de 156 962 : donc D S sera de 62 163. Mais C L est aussi déterminée, et contient 99 324 parties, comme il a été dit n^os 34 et 40, donc la raison de P D à D S sera comme de 99 324 à 62 163. Et ainsi l’on sait le rehaussement du point du fond I par la réfraction de cette section ; et il paraît que ce rehaussement
Fig. 40. est plus grand que par la réfraction de la section précédente, puisque la raison de P D à D S était là comme de 99 324 à 70 283.

Mais par la réfraction régulière du cristal, dont nous avons dit ci-dessus que la proportion était de 5 à 3, le rehaussement du point I ou P du fond sera de 2/5 de la hauteur D P ; comme il paraît par cette figure (Fig. 40), où le point P étant vu par les rayons P C R, P c r, également rompus en la surface C c, il faut que ce point paraisse en S, dans la perpendiculaire P D, où concourent les droites R C, r c prolongées : et l’on sait que la ligne P C à C S est comme 5 à 3, puisqu’elles sont entre elles comme le sinus de l’angle C S P ou D S C, au sinus de l’angle S P C. Et parce que les deux yeux R r étant supposés beaucoup éloignés au-dessus du cristal, la raison de P D à D S est censée la même que P C à C S, le rehaussement P S sera aussi de 2/5 de P D.

42. Que si l’on prend une ligne droite A B pour l’épaisseur du cristal, duquel le point B soit dans le fond, et qu’on la divise, suivant les proportions des rehaussements trouvées, aux points C, D, E, faisant A E de 3/5 A B, A B à A C comme 99 324 à 70 283, et A B à A D comme 99 324 à 62 163, ces points diviseront A B comme dans cette figure. Et l’on trouvera que ceci s’accorde parfaitement avec l’expérience, c’est-à-dire qu’en plaçant les yeux dans le plan qui coupe le cristal suivant le petit diamètre du rhombe de dessus, la réfraction régulière élèvera les lettres en E, et on verra le fond, et les lettres sur lesquelles il est posé, élevées en D par la réfraction irrégulière. Mais en plaçant les yeux dans le plan qui coupe le cristal suivant le grand diamètre du rhombe de dessus, la réfraction régulière élèvera les lettres en E comme auparavant, mais la réfraction irrégulière les fera en même temps paraître élevées en C seulement. En sorte que l’intervalle C E sera quadruple de l’intervalle E D, qu’on voyait auparavant.

43. Je n’ai que faire de remarquer ici que, dans toutes les deux positions des yeux, les images, causées par la réfraction irrégulière, ne paraissent pas directement au-dessous de celles qui procèdent de la réfraction régulière, mais qu’elles s’en écartent, en s’éloignant davantage de l’angle solide équilatéral du cristal ; parce que cela s’ensuit de tout ce qui a été démontré jusqu’ici de la réfraction irrégulière, et qu’il est surtout évident par ces dernières démonstrations, où l’on voit que le point I paraît par la réfraction irrégulière en S, dans la perpendiculaire D P, dans laquelle doit aussi paraître l’image du point P par la réfraction régulière, mais non pas l’image du point I, qui sera à peu près directement au-dessus de ce même point, et plus haute que S.

Mais pour ce qui est du rehaussement apparent du point I dans les autres positions des yeux au-dessus du cristal, outre les deux positions que nous venons d’examiner, l’image de ce point paraîtra, toujours par la réfraction régulière entre les deux hauteurs de D et C, passant de l’une à l’autre, à mesure qu’on tourne à l’entour du cristal immobile en regardant dessus. Et tout ceci se trouve encore conforme à notre hypothèse, comme un chacun pourra s’en assurer, après que j’aurai montré ici la manière de trouver les réfractions irrégulières, qui appartiennent à toutes les autres sections du cristal, outre les deux que nous avons considérées. Posons quelqu’une des faces du cristal, dans laquelle soit l’ellipse H D E (Fig. 42), dont le centre C soit aussi le centre du sphéroïde H M E, dans lequel s’étend la lumière, et dont ladite ellipse est la section. Et que le rayon incident soit R C, dont il faille trouver la réfraction.

Soit mené un plan passant par le rayon R C, et qui soit perpendiculaire au plan de l’ellipse H D E, le coupant suivant la droite B C K ; et ayant dans le même plan par R C fait C O perpendiculaire à C R, soit dans l’angle O C K ajustée O K perpendiculaire à O C et égale à la ligne N, que je suppose marquer le trajet de la lumière en l’air, dans le temps qu’elle s’étend dans le cristal par le sphéroïde H D E M.
Fig. 42. Puis dans le plan de l’ellipse H D E soit, par le point K, menée K T perpendiculaire à B C K. Maintenant si l’on conçoit un plan mené par la droite K T, et qui touche le sphéroïde H M E en I, la droite C I sera la réfraction du rayon R C, comme il est assez aisé à conclure de ce qui a été démontré au n^o 36.

Mais il faut montrer comment on peut déterminer le point de contact I. Soit menée à la ligne K T une parallèle H F, qui touche l’ellipse H D E, et que ce point de contact soit en H ; et ayant tiré une droite par C H, qui rencontre K T en T, soit imaginé par là même C H, et par C M, que je suppose être la réfraction du rayon perpendiculaire, un plan qui fasse dans le sphéroïde la section elliptique H M E (Fig. 43). Il est certain que le plan qui passera par la droite K T, et qui touchera le sphéroïde, le touchera dans un point de l’ellipse H M E, par le lemme qui sera démontré à la fin du chapitre. Or ce point est nécessairement le point I que l’on cherche, puisque le plan mené par T K ne peut toucher le sphéroïde qu’en un point. Et ce point I est aisé à déterminer, puisqu’il
Fig. 43. ne faut que mener du point T, qui est dans le plan de cette ellipse, la tangente T I, de la manière qui a été montrée ci-devant. Car l’ellipse H M E est donnée, dont C H et C M sont [des] demi-diamètres conjugués ; parce qu’une droite menée par M, parallèle à H E, touche l’ellipse H M E, comme il s’ensuit de ce qu’un plan mené par M, et parallèle au plan H D E, touche le sphéroïde en ce point M, ce qui se voit n^o 27 et 23. Au reste la position de cette ellipse, à l’égard du plan par le rayon R C et par C K, est aussi donnée, par où il sera aisé de trouver la position de la réfraction C I, à l’égard du rayon R C.

Or il faut noter, que la même ellipse H M E sert à trouver les réfractions de tout autre rayon qui sera dans le plan par R C et C K. Parce que tout plan, parallèle à la droite H F, ou T K, qui touchera le sphéroïde, le touchera dans cette ellipse, par le lemme cité peu devant.

Fig. 44.

J’ai recherché ainsi par le menu les propriétés de la réfraction irrégulière de ce cristal, pour voir si chaque phénomène, qui se déduit de notre hypothèse, conviendrait avec ce qui s’observe en effet. Ce qui étant ainsi, ce n’est pas une légère preuve de la vérité de nos suppositions et principes. Mais ce que je vais ajouter ici les confirme encore merveilleusement. Ce sont les coupes différentes de ce cristal, dont les surfaces, qu’elles produisent, font naître des réfractions précisément telles qu’elles doivent être, et que je les avais prévues, suivant la théorie précédente.

Pour expliquer quelles sont ces coupes, soit A B K F (Fig. 44) la section principale par l’axe du cristal, A C K, dans laquelle sera aussi l’axe S S d’une onde sphéroïde de lumière étendue dans le cristal du centre C ; et la ligne droite, qui coupe S S par le milieu, et à angles droits, savoir P P, sera un des grands diamètres.

Or comme dans la coupe naturelle du cristal, faite par un plan parallèle à deux surfaces opposées, lequel plan est ici représenté par la ligne G G, la réfraction des surfaces qui en sont produites se règle par les demi-sphéroïdes G N G, suivant ce qui a été expliqué dans la théorie précédente, de
Fig. 45. même en coupant le cristal par N N (Fig. 45), d’un plan perpendiculaire au parallélogramme A B K F, la réfraction des surfaces se devra régler par les demi-sphéroïdes N G N ; et si on le coupe par P P, perpendiculairement au dit parallélogramme, la réfraction des surfaces se devra régler par les demi-sphéroïdes P S P, et ainsi des autres. Mais je vis que si le plan N N était presque perpendiculaire au plan G G, faisant l’angle N C G, qui est du côté A, de 90 degrés 40 minutes, les demi-sphéroïdes N G N devenaient semblables aux demi-sphéroïdes G N G, puisque les plans N N et G G étaient inclinés également d’un angle de 45 degrés 20 minutes sur l’axe S S. Par conséquent il fallait, si notre théorie était vraie, que les surfaces que produit la section par N N, fissent toutes les mêmes réfractions que les surfaces de la section par G G. Et non pas seulement les surfaces de la section N N, mais toutes les autres, produites par des plans qui fussent inclinés à l’axe S S d’un angle pareil de 45 degrés 20 minutes. De sorte qu’il y avait une infinité de coupes, qui devaient produire précisément les mêmes réfractions que les surfaces naturelles du cristal, ou que la coupe parallèle à quelqu’une de ces surfaces, qui se fait en le fendant.

Je vis aussi qu’en le coupant d’un plan mené par P P, et perpendiculaire à l’axe S S, la réfraction des surfaces devait être telle que le rayon perpendiculaire n’en souffrît point du tout, et que toutefois aux rayons obliques il y eut une réfraction irrégulière, différente de la régulière, et par laquelle les objets, placés sous le cristal, fussent moins rehaussés que par cette autre.

Que de même, en coupant le cristal de quelque plan par l’axe S S, comme est le plan de cette figure, le rayon perpendiculaire ne devait point souffrir de réfraction, et que pour les rayons obliques, il y avait des mesures différentes pour la réfraction irrégulière, suivant la situation du plan où était le rayon incident.

Or ces choses se trouvèrent ainsi en effet, et je ne pus douter après cela qu’il ne se rencontrât partout un succès pareil. D’où je conclus que l’on peut former de ce cristal des solides semblables à ceux qui lui sont naturels, qui produiront, dans toutes leurs surfaces, les mêmes réfractions régulières et irrégulières que les surfaces naturelles, et qui pourtant se fendront tout autrement, et point parallèlement à aucune des faces.

Que l’on en peut faire aussi des pyramides, ayant la base carrée, pentagone, hexagone, ou de tant de côtés que l’on voudra, dont toutes les surfaces aient les mêmes réfractions que les surfaces naturelles du cristal, hormis la base, qui ne rompra point le rayon perpendiculaire. Ces surfaces feront chacune avec l’axe du cristal un angle de 45 degrés 20 minutes, et la base sera la section perpendiculaire à l’axe.

Qu’enfin on en peut aussi faire des prismes triangulaires, ou de tant de côtés qu’on veut, dont ni les côtés ni les bases ne rompront point le rayon perpendiculaire, quoique pourtant ils fassent tous double réfraction aux rayons obliques. Le cube est compris parmi ces prismes, dont les bases sont des sections perpendiculaires à l’axe du cristal, et les côtés sont des sections parallèles à ce même axe.

De tout ceci il paraît encore, que ce n’est point du tout dans la disposition des couches dont ce cristal paraît composé, et selon lesquelles il se fend en trois sens différents, que réside la cause de la réfraction irrégulière, et que ce serait en vain de l’y vouloir chercher.

Mais afin qu’un chacun, qui aura de cette pierre, puisse trouver, par sa propre expérience, la vérité de ce que je viens d’avancer, je dirai ici la manière dont je me suis servi à la tailler et à la polir. La taille est aisée par les roues tranchantes des lapidaires, ou de la manière qu’on scie le marbre, mais le poli est très difficile et, en employant les moyens ordinaires, on dépolit bien plutôt les surfaces qu’on ne les rend luisantes.

Après plusieurs essais, j’ai enfin trouvé qu’il ne faut point de plaque de métal pour cet usage, mais une pièce de glace de miroir rendue mate et dépolie. Là-dessus, avec du sablon fin et de l’eau, l’on adoucit peu à peu ce cristal, de même que les verres de lunettes, et on le polit en continuant seulement le travail, et en diminuant toujours la matière. Je n’ai su pourtant le rendre d’une clarté et transparence parfaites ; mais l’égalité, qu’acquièrent les surfaces, fait que l’on y observe mieux les effets de la réfraction, que dans celles qui se sont faites en fendant la pierre, qui ont toujours quelque inégalité.

Lors même que la surface n’est que médiocrement adoucie, si on la frotte avec un peu d’huile, ou de blanc d’œuf, elle devient fort transparente, en sorte que la réfraction s’y découvre fort distinctement. Et cette aide est surtout nécessaire, lorsqu’on veut polir les surfaces naturelles, pour en ôter les inégalités, parce qu’on ne saurait les rendre luisantes à l’égal de celles des autres sections, qui prennent d’autant mieux le poli qu’elles sont moins approchantes de ces plans naturels.

Devant que de finir le traité de ce cristal, j’ajouterai encore un phénomène merveilleux, que j’ai découvert après avoir écrit tout ce que dessus. Car bien que je n’en aie pas pu trouver jusqu’ici la cause, je ne veux pas laisser pour cela de l’indiquer, afin de donner occasion à d’autres de la chercher. Il semble qu’il faudrait faire encore d’autres suppositions outre celles que j’ai faites, qui ne laisseront pas pour cela de garder toute leur vraisemblance, après avoir été confirmées par tant de preuves.

Le phénomène est, qu’en prenant deux morceaux de ce cristal, et les appliquant l’un sur l’autre, ou bien les tenant avec de l’espace entre deux, si tous
Fig. 46. les côtés de l’un sont parallèles à ceux de l’autre, alors un rayon de lumière, comme A B (Fig. 46), s’étant partagé en deux dans le premier morceau, savoir en B D et en B C, suivant les deux réfractions, régulière et irrégulière, en pénétrant de là à l’autre morceau, chaque rayon y passera sans plus se partager en deux ; mais celui qui a été fait de la réfraction régulière, comme ici D G, fera seulement encore une réfraction régulière en G H, et l’autre, C E, une irrégulière en E F. Et la même chose arrive non seulement dans cette disposition, mais aussi dans toutes celles où la section principale, de l’un et de l’autre morceau, se trouve dans un même plan, sans qu’il soit besoin que les deux surfaces qui se regardent soient parallèles. Or il est merveilleux pourquoi les rayons C E et D G (Fig. 47), venant de l’air sur le cristal inférieur, ne se partagent pas de même que le premier rayon A B. On dirait qu’il faut
Fig. 47. que le rayon D G, en passant par le morceau de dessus, ait perdu ce qui est nécessaire pour émouvoir la matière qui sert à la réfraction irrégulière, et que C E ait pareillement perdu ce qu’il faut pour émouvoir la matière qui sert à la réfraction régulière, mais il y a encore autre chose qui renverse ce raisonnement. C’est que quand on dispose les deux cristaux en sorte, que les plans qui font les sections principales se coupent à angles droits, soit que les surfaces qui se regardent soient parallèles ou non, alors le rayon qui est venu de la réfraction régulière, comme D G, ne fait plus qu’une réfraction irrégulière dans le morceau inférieur, et au contraire le rayon qui est venu de la réfraction irrégulière, comme C E, ne fait plus qu’une réfraction régulière.

Mais dans toutes les autres positions infinies, outre celles que je viens de déterminer, les rayons D G, C E se partagent derechef chacun en deux, par la réfraction du cristal inférieur ; de sorte que du seul rayon A B il s’en fait quatre, tantôt d’égale clarté, tantôt de bien moindre les uns que les autres, selon la diverse rencontre des positions des cristaux, mais qui ne paraissent pas avoir plus de lumière tous ensemble que le seul rayon A B.

Quand on considère ici que, les rayons C E, D G demeurant les mêmes, il dépend de la position qu’on donne au morceau d’en bas de les partager chacun en deux, ou de ne les point partager, là où le rayon A B se partage toujours, il semble qu’on est obligé de conclure que les ondes de lumière, pour avoir passé le premier cristal, acquièrent certaine forme ou disposition, par laquelle en rencontrant le tissu du second cristal, dans certaine position, elles puissent émouvoir les deux différentes matières qui servent aux deux espèces de réfractions ; et en rencontrant ce second cristal dans une autre position, elles ne puissent émouvoir que l’une de ces matières. Mais pour dire comment cela se fait, je n’ai rien trouvé jusqu’ici qui me satisfasse.

Laissant donc à d’autres cette recherche, je passe à ce que j’ai à dire touchant la cause de la figure extraordinaire de ce cristal, et pourquoi il se fend aisément en trois sens différents, parallèlement à quelqu’une de ses surfaces.

Il y a plusieurs corps végétaux, minéraux, et sels congelés qui se forment avec de certains angles et figures régulières. Ainsi parmi les fleurs il y en a beaucoup, qui ont leurs feuilles disposées en polygones ordonnés, au nombre de 3, 4, 5 ou 6 côtés, mais non pas davantage. Ce qui mérite bien d’être remarqué, tant la figure polygone, que pourquoi elle n’excède pas ce nombre de 6.

Le cristal de roche croît ordinairement en bâtons hexagones, et l’on trouve des diamants qui naissent avec une pointe carrée, et des surfaces polies. Il y a une espèce de petites pierres plates, entassées directement les unes sur les autres, qui sont toutes de figure pentagone, avec les angles arrondis et les côtés un peu pliés en dedans. Les grains de sel gris, qui naissent de l’eau de mer, affectent la figure, ou du moins l’angle, du cube ; et dans les congélations d’autres sels, et de celles du sucre, l’on trouve d’autres angles solides, avec des surfaces parfaitement plates. La neige menue tombe presque toujours formée en petites étoiles à six pointes, et quelquefois en hexagones dont les côtés sont droits. Et j’ai souvent observé, au dedans de l’eau qui commence à se geler, une manière de feuilles plates et déliées de glace, dont la raie du milieu jette des branches inclinées d’un angle de 60 degrés. Toutes ces choses méritent d’être recherchées soigneusement, pour reconnaître comment et par quel artifice la nature y opère. Mais ce n’est pas maintenant mon dessein de traiter entièrement cette matière. Il semble qu’en général la régularité, qui se trouve dans ces productions, vient de l’arrangement des petites particules invisibles et égales dont elles sont composées. Et pour venir à notre cristal d’Islande, je dis que s’il avait une pyramide comme A B C D, (Fig. 48), composée de petits corpuscules ronds, non pas sphériques, mais sphéroïdes plats, tels que se feraient par la conversion de cette ellipse G H sur son petit diamètre E F, dont la proportion au grand est
Fig. 48. fort près celle de 1 à la racine carrée de 8. Je dis donc que l’angle solide de la pointe D, serait égal à l’angle obtus et équilatéral de ce cristal. Je dis de plus, si ces corpuscules étaient légèrement collés ensemble, qu’en rompant cette pyramide, elle se casserait suivant des faces parallèles à celles qui font la pointe, et que par ce moyen, comme il est aisé de voir, elle produirait des prismes semblables à ceux du même cristal, tels que représente cette autre figure (Fig. 49). La raison est, qu’en se cassant de cette façon, toute une couche se sépare aisément de sa couche voisine, parce que chaque sphéroïde ne se détache que des trois sphéroïdes de l’autre couche, desquels trois il n’y en a qu’un qui le touche par la surface aplatie, et les deux autres seulement par les bords. Et ce qui fait que les surfaces se séparent nettes et polies, c’est que si quelque sphéroïde de la couche voisine voulait en sortir pour s’attacher
Fig. 49. à celle qui se sépare, il faudrait qu’il se détachât des six autres sphéroïdes qui le tiennent serré, et dont les quatre le pressent par ces surfaces aplaties. Puis donc que tant les angles de notre cristal, que la manière dont il se fend, conviennent justement avec ce qui se remarque au composé de tels sphéroïdes, c’est une grande raison pour croire que ses particules sont formées et rangées de même.

Il y a même assez d’apparence que les prismes de ce cristal se font par la rupture des pyramides, puisque M. Bartholin rapporte qu’il s’en trouve parfois des morceaux de figure pyramidale triangulaire. Mais quand une masse ne serait composée qu’intérieurement de ces petits sphéroïdes ainsi entassés, quelque forme qu’elle eût par dehors, il est certain, par la même, raison que je viens d’expliquer, qu’étant cassée elle produirait des prismes pareils. Il reste à voir s’il y a d’autres raisons qui confirment notre conjecture, et s’il n’y en a point qui y répugnent.

L’on peut objecter que ce cristal, étant ainsi composé, se pourrait fendre encore en deux manières, dont l’une serait suivant des plans parallèles à la base de la pyramide, c’est-à-dire au triangle A B C,
Fig. 50. l’autre parallèlement à un plan dont la coupe est marquée par les lignes G H, H K, K L (Fig. 50). À quoi je dis, que l’une et l’autre division, quoique faisables, sont plus malaisées que celles qui étaient parallèles à quelqu’un des trois plans de la pyramide ; et qu’ainsi, en frappant sur le cristal pour le casser, il se doit toujours fendre plutôt suivant ces trois plans que suivant les deux autres. Quand on a un nombre de sphéroïdes de la forme ci-devant marquée, et qu’on les range en pyramide, on voit pourquoi les deux divisions sont plus malaisées. Car pour ce qui est de celle qui se ferait parallèlement à la base, chaque sphéroïde se doit détacher des trois autres qu’il touche par les surfaces aplaties, qui tiennent plus que ne font les contacts par les bords. Et outre cela, cette division ne se fera point par des couches entières, parce qu’un chacun des sphéroïdes d’une couche n’est presque point retenu par les six de la même couche qui l’environnent, parce qu’ils ne le touchent que par les bords ; de sorte qu’il adhère aisément à la couche voisine, et d’autres à lui, par la même raison, ce qui cause des surfaces inégales. Aussi voit-on par expérience, qu’en usant le cristal sur une pierre un peu rude, directement sur l’angle solide équilatéral, on trouve à la vérité beaucoup de facilité à le diminuer en ce sens, mais beaucoup de difficulté ensuite à polir la surface qu’on aura aplatie de cette manière.

Pour l’autre division suivant le plan G H K L, l’on verra que chaque sphéroïde s’y devrait détacher de quatre de la couche voisine, dont deux le touchent par les surfaces aplaties, et deux par les bords. De sorte que cette division est de même plus difficile que celle qui se fait parallèlement à une des surfaces du cristal, où nous avons dit que chaque sphéroïde ne se détache que de trois de sa couche voisine, dont il n’y en a qu’un qui le touche par la surface aplatie, et les deux autres par les bords seulement.

Cependant, ce qui m’a fait connaître qu’il y a dans le cristal des couches de cette dernière façon, c’est qu’en un morceau de demi-livre que j’ai, l’on voit qu’il est fendu tout du long, ainsi que le prisme susdit par le plan G H K L, ce qui paraît par les couleurs d’iris répandues dans tout ce plan, quoique les deux pièces tiennent encore ensemble. Tout ceci prouve donc que la composition du cristal est telle que nous avons dit. À quoi j’ajoute encore cette expérience, que si on passe un couteau en raclant sur quelqu’une de ces surfaces naturelles, et que ce soit en descendant de l’angle obtus équilatéral, c’est-à-dire de la pointe de la pyramide, on le trouve fort dur, mais en raclant du sens contraire on l’entame aisément. Ce qui s’ensuit manifestement de la situation des petits sphéroïdes, sur lesquels, dans la première manière, le couteau glisse ; mais dans l’autre il les prend par dessous, à peu près comme les écailles d’un poisson.

Je n’entreprendrai pas de rien dire touchant la manière dont s’engendrent tant de petits corpuscules, tous égaux et semblables, ni comment ils sont mis dans un si bel ordre. S’ils sont formés premièrement et puis assemblés, ou s’ils se rangent ainsi en naissant, et à mesure qu’ils sont produits, ce qui me paraît plus vraisemblable. Il faudrait pour développer des vérités si cachées une connaissance de la nature bien plus grande que celle que nous avons. J’ajouterai seulement que ces petits sphéroïdes pourraient bien contribuer à former les sphéroïdes des ondes de lumière, ci-dessus supposés, les uns et les autres étant situés de même, et avec leurs axes parallèles.

Calculs qui ont été supposés dans ce Chapitre.

M. Bartholin dans son traité de ce cristal, met les angles obtus des faces de 101 degrés, lesquels j’ai dit être de 101 degrés 52 minutes. Il dit avoir mesuré immédiatement ces angles sur le cristal, ce qui est difficile à faire avec la dernière justesse, à cause que les carnes, comme C A, C B dans cette figure (Fig. 51), sont ordinairement usées, et non pas bien droites. Pour plus de sûreté donc, j’ai plutôt voulu mesurer actuellement l’angle obtus, duquel
Fig. 51. sont inclinées l’une sur l’autre les faces C B D A, C B V F, savoir l’angle O C N, après avoir mené C N perpendiculaire sur F V, et C O perpendiculaire sur D A, lequel angle O C N j’ai trouvé de 105 degrés et son complément à deux angles droits, C N P, de 75 degrés, comme il fallait.

Pour trouver par là l’angle obtus B C A, je me suis imaginé une sphère, ayant son centre en C, et dans sa superficie un triangle sphérique, formé par l’intersection des trois plans qui comprennent l’angle solide C. Dans ce triangle équilatéral, qui soit A B F dans cette autre figure (Fig. 52), je voyais que chacun des angles devait être de 105 degrés, savoir égal à l’angle O C N, et que chacun des côtés était d’autant de degrés que l’angle A C B, A C F, ou B C F. Ayant donc mené l’arc F Q perpendiculaire sur le côté A B, qu’il divise également en Q, le triangle F Q A avait l’angle Q droit, l’angle A de 105 degrés, et F de la moitié autant, savoir de 52 degrés 30 minutes, d’où se trouve l’hypoténuse A F de 101 degrés 52 minutes. Et cet arc A F est la mesure de l’angle A C F dans la figure du cristal.

Fig. 52.

Dans la même figure (Fig. 51), si le plan C G H F coupe le cristal en sorte, qu’il divise les angles obtus A C B, M F V par le milieu il a été dit, au nombre 10, que l’angle C F H est de 70 degrés 57 minutes. Ce qui se démontre encore facilement dans le même triangle sphérique A B F, où il paraît que l’arc F Q est d’autant de degrés que l’angle G C F dans le cristal, duquel le complément à deux droits est l’angle C F H. Or l’arc F Q se trouve de 109 degrés 3 minutes. Donc son complément, 70 degrés 57 minutes, est l’angle C F H.

Il a été dit, n^o 26, que la droite C S, qui dans la précédente figure, soit C H (Fig. 51), étant l’axe du cristal, c’est-à-dire également inclinée aux trois côtés C A, C B, C F, l’angle G C H est de 45 degrés 20 minutes, ce qui se calcule encore facilement par le même triangle sphérique. Car en tirant l’autre arc A D, qui coupe B F également, et F Q en S, ce point sera le centre de ce triangle ; et il est aisé de voir que l’arc S Q est la mesure de l’angle G C H, dans la figure qui représente le cristal. Or dans le triangle Q A S (Fig. 53), qui est rectangle, l’on connaît aussi l’angle A, qui est de 52 degrés 30 minutes, et le côté A Q de 50 degrés 56 minutes, d’où se trouve le côté S Q de 45 degrés 20 minutes.

Fig. 53.

Au nombre 27, il faut montrer que P M S étant une ellipse dont le centre est C, et qui touche la droite M D en M, en sorte que l’angle M C L, que fait C M avec C L, perpendiculaire sur D M, soit de 6 degrés 40 minutes, et son demi-petit diamètre C S faisant avec C G, parallèle à M D, un angle G C S de 45 degrés 20 minutes, il faut montrer, dis-je, que C M étant de 100 000 parties, P C, demi-grand diamètre de cette ellipse, est de 105 032, et C S, demi-petit diamètre, de 93 410.

Soient C P, C S (Fig. 54) prolongées, et qu’elles rencontrent la tangente D M en D et Z ; et du point de contact M soient menées M N, M O perpendiculaires sur C P, C S. Maintenant parce que les angles S C P, G C L sont droits, l’angle P C L sera égal à G C S, qui était de 45 degrés 20 minutes. Et ôtant l’angle L C M, qui est de 6 degrés 40 minutes, de L C P 45 degrés 20 minutes, reste M C P de 38 degrés 40 minutes. Considérant donc C M comme rayon de 100 000 parties, M N, sinus de 38 degrés 40 minutes sera 62 479. Et dans le triangle rectangle M N D, M N sera à N D comme le rayon des Tables à la tangente de 45 degrés 20 minutes, parce que l’angle M N D est égal à D C L ou G C S, c’est-à-dire comme 100 000 à 101 170, d’où vient N D 63 210. Mais N C est de 78 079 des mêmes parties dont C M est 100 000, parce que N C est sinus du complément
Fig. 54. de l’angle M C P, qui était de 38 degrés 40 minutes. Donc toute la D C est de 141 289 ; et C P, qui est moyenne proportionnelle entre D C et C N, parce que M D touche l’ellipse, sera 105 032.

De même, parce que l’angle O M Z est égal à C D Z, ou L C Z, qui est de 44 degrés 40 minutes, étant le complément de G C S, il s’ensuit que, comme le rayon des tables à la tangente de 44° 40′, ainsi sera O M 78 079, à O Z 77 176. Mais O C est de 62 479 de ces mêmes parties dont C M est 100 000, parce qu’elle est égale à M N, sinus de l’angle M C P de 38° 40′. Donc toute la C Z est 139 655, et C S, qui est moyenne proportionnelle entre C Z, C O, sera 93 410.

Au même endroit on a dit que C G se trouve de 98 779 parties. Pour le démontrer, soit dans la même figure menée P E parallèle à D M, et qui rencontre C M en E. Dans le triangle C L D, le côté C L est 99 324 (C M étant 100 000), parce que C L est sinus du complément de l’angle L C M, de 6° 40′. Et puisque l’angle L C D est de 45° 20′, pour être égal à G C S, l’on trouvera le côté L D 100 486, d’où ôtant M L 11 609, restera M D 88 877. Or comme C D, qui était 141 289, à D M 88 877, ainsi C P 105 032, à P E 66 070. Mais comme le rectangle M E H, ou bien la différence des carrés C M, C E, au carré M C, ainsi est le carré P E au carré C g ; donc aussi comme la différence des carrés D C, C P au carré de C D, ainsi le carré P E au carré C g. Mais D P, C P et P E sont connues : on connaît donc aussi G C, qui est 98 779.

Lemme qui a été supposé.

Si un sphéroïde est touché par une ligne droite, et aussi par deux ou plusieurs plans qui soient parallèles à cette ligne, quoique non pas entre eux, tous les points du contact, tant de la ligne que des plans, seront dans une même ellipse, faite par un plan qui passe par le centre du sphéroïde.

Soit le sphéroïde L E D (Fig. 55) touché par la ligne B M au point B, et aussi par des plans, parallèles à cette ligne, aux points O et A. Il faut démontrer que les points B, O, et A, sont dans une même ellipse, faite dans le sphéroïde par un plan qui passe par son centre.

Par la ligne B M et par les points O, A, soient menés des plans parallèles entre eux, qui, en coupant le sphéroïde, fassent les ellipses L B D, P O P, Q A Q, qui seront toutes semblables et semblablement posées, et auront leurs centres K, N, R, dans un même diamètre du sphéroïde, qui sera aussi diamètre
Fig. 55. de l’ellipse faite par la section du plan qui passe par le centre du sphéroïde, et qui coupe les plans des trois susdites ellipses à angles droits ; car tout cela est manifeste par la prop. 15, du livre des Conoïdes et Sphéroïdes d’Archimède. De plus, les deux derniers plans, qui ont été menés par les points O, A, seront aussi, en coupant les plans qui touchaient le sphéroïde en ces mêmes points, des lignes droites, comme O H, A S, qui seront, comme il est aisé de voir, parallèles à B M ; et toutes les trois, B M, O H, A S, toucheront les ellipses L B D, P O P, Q A Q, dans ces points B, O, A, puisqu’elles sont dans les plans de ces ellipses, et en même temps dans des plans qui touchent le sphéroïde. Que si maintenant de ces points B, O, A, l’on mène des droites B K, O N, A R, par les centres des mêmes ellipses, et que par ces centres l’on mène aussi les diamètres L D, P P, Q Q, parallèles aux touchantes B M, O H, A S, ces diamètres seront les conjugués des susdits B K, O N, A R. Et parce que les trois ellipses sont semblables et semblablement posées, et qu’elles ont leurs diamètres L D, P P, Q Q, parallèles, il est certain que leurs diamètres conjugués B K, O N, A R, seront aussi parallèles. Et les centres K, N, R, étant, comme il a été dit, dans un même diamètre du sphéroïde, ces parallèles B K, O N, A R, seront nécessairement dans un même plan, qui passe par ce diamètre du sphéroïde, et par conséquent les points B, O, A, dans une même ellipse faite par l’intersection de ce plan : ce qu’il fallait prouver. Et il est manifeste que la démonstration serait la même, si, outre les points O, A, il y en avait d’autres, dans lesquels le sphéroïde fût touché par des plans parallèles à la droite B M.

---