Œuvres de Lagrange/Pièces diverses/Remarques sur la méthode des projections pour le calcul des éclipses de Soleil ou d’étoiles

Joseph-Louis Lagrange

Remarques sur la méthode des projections pour le calcul des éclipses de Soleil ou d’étoiles

Pièces diverses non comprises dans les recueils académiques, Gauthier-Villars, 1868, Œuvres de Lagrange. Tome VII (p. 393-412).

REMARQUES
SUR
LA MÉTHODE DES PROJECTIONS
POUR LE
CALCUL DES ÉCLIPSES DE SOLEIL OU D’ÉTOILES^[1].

---

(Connaissance des Temps ou des Mouvements célestes, à l’usage des Astronomes et des Navigateurs, pour l’an 1819 ; publiée par le Bureau des Longitudes. — 1816.)

1. Parmi les différentes méthodes que les Astronomes ont imaginées pour faciliter le calcul des éclipses de Soleil, et en général de toutes les éclipses sujettes aux parallaxes, on doit regarder, ce me semble, celle des projections comme une des plus ingénieuses et des plus simples. On en attribue ordinairement l’invention à Kepler ; mais il paraît que ce grand Astronome n’est, à proprement parler, que l’auteur de l’idée heureuse de considérer les éclipses de Soleil comme des éclipses de Terre, et de déterminer les phases de l’éclipse générale, c’est-à-dire les circonstances de l’éclipse pour la Terre en général par la considération de la route du centre de l’ombre de la Lune sur le plan du disque de la Terre illuminé. (Voir le sixième Livre de son Epitome Astronomiæ, où cette méthode est expliquée et appliquée à quelques exemples.) Pour déterminer les phases d’une éclipse pour un lieu particulier de la Terre, il ne suffit pas de considérer la trace de l’ombre sur le plan du disque de la Terre ; il faut aussi considérer celle du lieu dont il s’agit, projeté sur le même plan, et c’est en quoi consiste proprement la méthode des projections.

Il paraît que Cassini est le premier qui ait proposé et pratiqué cette méthode dans un écrit italien, imprimé à Ferrare en 1664 ; depuis, elle a été adoptée et mise en usage par la plupart des Astronomes ; on la trouve surtout employée et développée avec beaucoup de détails dans les Tables astronomiques, publiées par La Hire au commencement de ce siècle, et dans celles que Cassini le fils a données en 1740 ; et il n’y a presque aucun Traité d’Astronomie où elle ne soit expliquée.

2. À considérer cette méthode d’une manière générale, elle ne consiste que dans la représentation en perspective de la marche du centre de l’ombre de la Lune et de celle des différents lieux de la Terre, en conséquence de la rotation diurne.

Comme le lieu de l’œil est arbitraire, ainsi que la position du plan du tableau ou de projection, il convient de les prendre en sorte qu’il en résulte la plus grande simplicité, surtout dans la projection de la route de l’ombre. C’est ce que l’on obtient en plaçant 1^o l’oeil dans le centre du Soleil, moyennant quoi la projection du centre de l’ombre de la Lune se trouve la même que celle du centre de la Lune, à cause que le centre de l’ombre est nécessairement dans le prolongement de la ligne droite qui passe par les centres du Soleil et de la Lune ; 2^o en prenant pour le plan de projection un plan perpendiculaire à l’écliptique et à la ligne menée du centre de la Terre au centre du Soleil qu’on nomme communément la ligne des centres, lequel touché en même temps l’orbite de la Lune ; car, comme la portion de l’orbite de la Lune, décrite pendant la durée d’une éclipse de Soleil, peut être prise sans erreur sensible pour une ligne droite, le centre de la Lune se trouvera dans le plan de projection, et y décrira une ligne droite dont la position sera facile à déterminer par les éléments de la Lune. De cette manière, toute la difficulté sera réduite à projeter sur le même plan la trace d’un lieu quelconque de la Terre pendant la durée de l’éclipse. 3. Si le Soleil était à une distance infinie de la Terre, toutes les droites menées des différents points de la surface de la Terre au centre du Soleil seraient parallèles entre elles et à la ligne des centres ; elles seraient par conséquent toutes perpendiculaires au plan de projection. On aurait donc le cas de la projection perpendiculaire ou orthographique, qui est de toutes la plus simple et la plus facile à exécuter. Dans ce cas, comme la projection est toujours la même sur tous les plans parallèles, quelle que soit leur distance, il n’y aura qu’à considérer la projection de la surface de la Terre sur le plan du disque terrestre éclairé par le Soleil, c’est-à-dire sur le plan du cercle de latitude qui coupe l’écliptique à $90$ degrés de part et d’autre du lieu du Soleil. On décrira donc d’abord un cercle qui représente la projection de l’hémisphère éclairé ; on mènera dans ce cercle de projection deux diamètres perpendiculaires entre eux, dont l’un représentera l’écliptique, et l’autre le cercle de latitude qui passe par le Soleil. On mènera ensuite un autre diamètre qui fasse avec ce dernier un angle égal à l’angle de position du Soleil dont la tangente est égale à la tangente de l’obliquité de l’écliptique, multipliée par le cosinus de la longitude du Soleil. Ce nouveau diamètre représentera le cercle de déclinaison du Soleil, et sera ce qu’on nomme le méridien universel, parce que, dans tous les lieux de la Terre qui s’y trouvent situés, on compte midi en même temps ; le diamètre sera aussi la projection de l’axe de la Terre, en sorte que les pôles et les centres des différents parallèles terrestres se trouveront nécessairement sur ce même diamètre ; pour déterminer la position des pôles, il n’y aura qu’à prendre, depuis le centre de la projection, une distance qui soit au rayon de la projection comme le cosinus de l’angle que fait l’axe de la Terre avec le plan de projection, angle qui est évidemment égal à la déclinaison du Soleil, est au sinus total ; et, pour déterminer le centre d’un parallèle dont la latitude est donnée, on prendra une distance qui soit à celle du pôle comme le sinus de la latitude donnée est au sinus total. Connaissant ainsi la projection du centre d’un parallèle donné, on pourra tracer celle de tout le parallèle, lequel sera projeté par une ellipse dont le grand axe sera perpendiculaire à la projection de l’axe de la Terre, et sera égal au diamètre même du parallèle (par conséquent il sera au rayon de la projection, comme le cosinus de la latitude donnée est au sinus total), et dont le petit axe sera au grand, comme le cosinus de l’angle que fait le plan du parallèle avec le plan de projection est au sinus total, c’est-à-dire comme le sinus de la déclinaison du Soleil est au sinus total, à cause que l’angle dont il s’agit est évidemment le complément de celui de l’axe de la Terre avec le plan de projection.

Cette ellipse ainsi tracée devra ensuite être divisée en heures et en minutes, si l’on veut, ce que l’on fera en divisant en autant de parties égales la circonférence d’un cercle décrit sur le grand axe de l’ellipse, et abaissant ensuite de chaque point de division des perpendiculaires sur l’axe ; les points d’intersection de ces perpendiculaires avec la circonférence de l’ellipse donneront les divisions des heures et minutes ; midi et minuit tomberont aux extrémités du petit axe, et $6$ heures se trouveront aux extrémités du grand axe.

De cette manière donc on aura la projection d’un lieu quelconque de la Terre dont la latitude est donnée, à une heure quelconque comptée au méridien de ce même lieu, et il n’y aura plus, pour achever la projection de l’éclipse, qu’à déterminer le lieu où le centre de la Lune sera dans un instant quelconque dans le même plan de projection.

4. Pour cela, on considérera qu’en prenant la distance de la Lune à la Terre pour l’unité, le rayon de la Terre devient égal à la parallaxe horizontale de la Lune, qui est l’angle sous lequel ce rayon paraît, vu du centre de la Lune ; ce sera donc la valeur du rayon du cercle de projection. Ensuite il est clair que, dans cette même hypothèse, les distances du lieu de la Lune dans le plan de projection aux diamètres qui représentent l’écliptique et le cercle de latitude seront égales à très-peu près à la latitude de la Lune et à la différence de sa longitude à celle du Soleil qui, vu du centre de la Terre, répond au centre de la projection. (Il faudrait prendre, à la vérité, à la place de ces angles leurs sinus ; mais, la différence étant très-petite, il est plus simple de prendre les angles mêmes.) Ainsi, connaissant par les Tables deux longitudes et deux latitudes correspondantes de la Lune, pour deux instants donnés, on placera ces deux lieux sur le plan de projection ; ensuite on mènera par ces deux points une ligne droite, qui représentera l’orbite relative de la Lune, et l’on divisera cette ligne en parties égales qui représentent les heures et les minutes, en sorte que les instants donnés tombent précisément aux points marqués. On aura, par ce moyen, le lieu du centre de la Lune dans un instant quelconque, ce qui est fondé sur ce que le mouvement relatif de la Lune au Soleil peut étrepris pour rectiligne et uniforme dans un court espace de temps, tel que celui de la durée d’une éclipse de Soleil.

5. Ce que nous venons de démontrer a lieu dans le cas où la distance du Soleil à la Terre serait réellement infinie. Supposons maintenant que le Soleil soit, ainsi qu’il l’est réellement, à une distance finie, quoique très-grande, de la Terre, et voyons quels sont les changements qui doivent en résulter dans la projection précédente. Et d’abord il est clair que la projection du centre de la Lune doit demeurer la même qu’auparavant, parce que ce centre est supposé placé dans le plan même de projection. Pour ce qui regarde ensuite la projection des lieux de la surface de la Terre, il est facile de concevoir que chaque point projeté devra être placé plus près du centre de la projection, en restant néanmoins sur le même rayon, et que sa nouvelle distance au centre de la projection devra être à la première distance, comme la distance du plan de projection au Soleil, c’est-à-dire la distance de la Lune au Soleil, est à la distance du centre de la Terré au Soleil moins la distance du lieu de la Terre dont on cherche la projection au plan passant par le centre de la Terre et parallèle au plan de projection. Or cette dernière distance, étant toujours nécessairement moindre que le rayon de la Terre, est comme infiniment petite par rapport à celle du Soleil, et peut par conséquent être négligée sans erreur sensible vis-à-vis de celle-ci ; donc il ne s’agira que de diminuer la distance entre chaque point projeté, au centre de la projection, dans la raison de la distance du Soleil à la Terre, à celle du Soleil à la Lune, c’est-à-dire dans la raison de la parallaxe de la Lune à la différence des parallaxes de la Lune et du Soleil. Or nous avons supposé (n^o 4) le rayon de la projection égal à la parallaxe de la Lune ; donc ce rayon deviendra égal à la parallaxe de la Lune moins celle du Soleil, et toutes les autres parties de la projection de la surface de la Terre devront être diminuées dans la même proportion, en conservant entre elles la même position mutuelle. Ainsi il n’y aura qu’à faire d’abord le rayon de la projection égal à la différence des parallaxes horizontales de la Lune et du Soleil, et procéder ensuite de la manière que nous avons expliquée plus haut.

6. La projection que nous venons de détailler représentera donc le mouvement de la Lune et les mouvements particuliers des différentes lieux de la Terre, vus du centre du Soleil sur un plan toujours perpendiculaire à la ligne qui joint les centres du Soleil et de la Terre, et touchant l’orbite même de la Lune, en sorte que cette planète soit mue réellement dans ce même plan. Or, si l’on imagine "un spectateur placé dans un lieu quelconque de la surface de la Terre, il est visible que ce spectateur rapportera le centre du Soleil sur le plan de projection au même point où un spectateur placé dans le Soleil aurait rapporté le lieu dont il s’agit de la surface de la Terre ; et quant au centre de la Lune, il paraîtra aux mêmes points du plan de projection qu’auparavant, puisqu’il est supposé placé réellement dans ce plan. Donc la même projection représentera aussi les positions respectives et la marche combinée des centres de la Lune et du Soleil, pour un spectateur placé sur un endroit quelconque de la surface de la Terre, pourvu que l’on rapporte maintenant au centre du Soleil la projection de ce lieu de la Terre, c’est-à-dire qu’on suppose à chaque instant le centre du Soleil dans la projection de ce même lieu. Or, par l’hypothèse du n^o 4, il est clair que toutes les parties de la projection sont proportionnelles aux angles sous lesquels ces parties paraîtraient, étant vues du centre de la Terre ; donc aussi les distances des centres du Soleil et de la Lune, vues par le spectateur dont on vient de parler, et mesurées sur la projection, seront proportionnelles aux angles sous lesquels elles paraîtraient, étant vues du centre de la Terre. Si ces distances étaient proportionnelles aux angles sous lesquels elles sont vues par le spectateur placé sur la surface de la Terre, alors leur valeur, mesurée sur l’échelle de la projection, donnerait les vrais angles des distances apparentes des centres du Soleil et de la Lune pour ce spectateur, et, étant comparées aux diamètres apparents de ces deux astres, serviraient à déterminer immédiatement les différentes phases de l’éclipsé pour le lieu de la Terre où le spectateur est supposé placé. Les Astronomes font tacitement cette supposition dans l’usage de la méthode des projections, en prenant les valeurs des distances mesurées sur la projection pour les vraies distances apparentes ; l’erreur qu’ils commettent par là est, à la vérité, assez petite, à cause de la petitesse du rapport du rayon de la Terre à celui de l’orbite de la Lune ; mais elle empêche toujours que la méthode dont il s’agit ait toute la précision qu’on y peut désirer.

7. Le grand avantage de cette méthode consiste principalement en ce qu’on peut exécuter toutes les opérations et déterminer les circonstances de l’éclipse avec la règle et le compas, ainsi qu’on le voit dans la plupart des Traités d’Astronomie. On peut aussi, pour plus de précision, calculer les différentes lignes de la projection par la Trigonométrie sphérique ; on en trouve la méthode dans les Tables de La Hire et de Cassini et dans les Leçons de La Caille ; mais alors le calcul devient presque aussi long que par la méthode ordinaire des parallaxes, et il est moins exact que par cette dernière méthode. On doit dire la même chose de la méthode proposée et employée par l’abbé de La Caille, dans les Mémoires de Paris pour 1744. Cette méthode consiste à calculer exactement, par les règles ordinaires de la perspective, la position du centre de la Lune et celle d’un lieu donné de la surface de la Terre sur le plan du disque éclairé de la Terre pour plusieurs instants, et à en déduire ensuite, par l’interpolation, les temps où la projection du lieu donné a été à une distance donnée de la projection du centre de la Lune ; M. de La Caille croit rectifier par là la méthode des projections, et il faut avouer que la projection est plus exacte par ses calculs que par les règles ordinaires ; mais l’erreur qu’on commet en prenant les distances mesurées sur la projection pour les vraies distances apparentes a lieu également dans la méthode de cet astronome, et il est étonnant qu’il ne s’en soit pas aperçu. Nous ferons voir ailleurs comment on peut rectifier à cet égard et simplifier même la méthode dont il s’agit.

8. Comme la principale difficulté à laquelle l’usage de la méthode des projections est sujet consiste à décrire les ellipses qui doivent représenter les différents parallèles terrestres ; que d’ailleurs ces ellipses doivent être toutes semblables pour une même projection du globe à l’égard du Soleil, c’est-à-dire, pour une même déclinaison du Soleil, mais seulement de différentes grandeurs, et placées à différentes distances du centre de la projection, suivant la latitude du parallèle correspondant, M. de Lalande a pensé que ce serait rendre un service essentiel à ceux qui voudraient pratiquer la méthode des projections, et contribuer en même temps à la perfection de cette méthode, en donnant des ellipses déjà tracées et divisées pour différents degrés de déclinaison du Soleil, avec une Table qui indiquerait la valeur du rayon de la projection, ainsi que la distance du centre de l’ellipse au centre de la projection, en parties du grand axe de l’ellipse, pour chaque latitude à laquelle l’ellipse doit répondre ; car, comme le rayon de la projection est arbitraire, rien n’empêche de le prendre tel qu’il puisse cadrer à une ellipse déjà tracée, et qu’on suppose devoir représenter un parallèle donné. (Voir les Mémoires de Paris pour 1763.) Cette idée heureuse de M. de Lalande a été adoptée et poussée plus loin par le P. Hell. Non seulement il a étendu la Table de M. de Lalande à tous les degrés de latitude et à tous les degrés de déclinaison jusqu’au vingt+uitième, qui est la limite au delà de laquelle aucun astre ne peut être éclipsé par la Lune ; mais, ce qui est encore plus important, il a pris la peine de calculer les abscisses et les ordonnées de chaque ellipse pour tous les points qui répondent aux divisions de dix en dix minutes ; de sorte qu’on peut, par le moyen de ses Tables, déterminer, avec toute la facilité et l’exactitude possibles, la trace d’un lieu quelconque de la Terre sur le cercle de projection, sans employer les opérations graphiques, toujours sujettes à erreur. Les Tables dont nous venons de parler sont imprimées à la suite des Éphémérides de l’année 1769, et mériteraient, ce me semble, une place dans les recueils de Tables astronomiques.

9. Feu M. Lambert a proposé un autre moyen de lever les difficultés attachées à la description des ellipses de projection. Comme ces ellipses résultent de la projection orthographique des parallèles terrestres, et que dans la projection stéréographique de la sphère, dans laquelle le plan de projection est un des grands cercles, et l’œil est supposé placé au pôle même de ce grand cercle, tous les cercles de la sphère se trouvent aussi projetés par des cercles, M. Lambert commence par projeter les parallèles terrestres stéréographiquement, en supposant l’œil sur la surface du globe et au nadir du Soleil ; ensuite, après avoir divisé les cercles projetés en heures et minutes, ce qui se fait par une construction fort simple, il change la projection stéréographique en orthographique par le moyen de deux échelles, dont l’une est divisée suivant les sinus des angles, et l’autre suivant les tangentes de la moitié de ces angles. En effet, il est visible que ; dans la projection orthographique, la distance de la projection d’un point quelconque de la surface de la sphère au centre de la projection est égale au sinus de l’arc compris entre ce point de la sphère et celui qui répond au centre de la projection, et que, dans la projection stéréographique, cette distance est égale à la tangente de la moitié du même arc. Ainsi, en appliquant la distance d’un point quelconque de la projection stéréographique au centre de la projection à l’échelle des tangentes, et prenant ensuite sur l’échelle des sinus la valeur de la distance qui répond au même arc, il n’y aura plus qu’à transporter cette dernière distance sur la projection, en partant du centre, et en la plaçant sur le même rayon sur lequel on avait pris la première distance. (Voir la deuxième Partie des Beiträge, etc., douzième Mémoire.) M. Lambert a encore tiré un autre parti de la projection stéréographique. Il trace d’abord, sur le plan du disque illuminé, la projection orthographique de la route du centre de la pénombre de la Lune sur la surface du globe, ce qui est facile. Il change ensuite, par des constructions assez simples, cette projection orthographique en stéréographique, mais faite sur le plan de l’équateur. Alors il applique sur cette dernière projection celle de l’hémisphère terrestre projeté de même et dessiné sur un papier transparent, en sorte que les deux projections soient visibles à la fois, et, faisant tourner cet hémisphère pour représenter la rotation de la Terre, il a un tableau continuel des lieux de la Terre qui entrent successivement dans l’ombre ou qui en sortent. Cette idée trbs-ingénieuse peut être appliquée en géneral à représenter l’état du ciel pour tous les pays de la Terre dans un instant quelconque, et peut être d’une grande utilité dans plusieurs occasions.

10. Voilà un exposé succinct des principes et des artifices principaux de la méthode des projections dont l’usage est si étendu dans toute l’Astronomie. Comme elle est détaillée et employée dans la plupart des Traités d’Astronomie, j’aurais pu me dispenser de l’expliquer ici ; mais il m’a paru que la manière dont on la présente ordinairement n’en donne pas une idée assez nette ; car, d’un côté, on emploie la projection orthographique pour déterminer la trace elliptique d’un lieu quelconque de la surface de la Terre sur le plan de projection, ce qui semble supposer qu’on regarde le Soleil comme infiniment éloigné de la Terre ; de l’autre, on prescrit de faire le rayon de la projection égal à la différence des parallaxes horizontales de la Lune et du Soleil, par la raison que le disque de la Terre projeté dans l’orbe de la Lune, et vu du centre du Soleil, c’est-à-dire vu à une distance très-grande, mais finie, doit paraître de cette grandeur, ce qui est évident de soi-même, mais ce qui paraît en même temps contraire à la première supposition de la projection orthographique. Parmi tant d’auteurs qui se sont copiés successivement, je n’en ai trouvé aucun qui ait remarqué cette contradiction apparente dans la méthode ordinaire des projections, ni-qui ait fait voir directement comment la seconde supposition sert à corriger à trèspeu près ce qu’il y a de défectueux dans la première. Je pense que la démonstration que j’en ai donnée ne doit laisser aucun doute sur ce point.

D’ailleurs il me semble que l’idée que l’on donne communément de la projection dans les éclipses est un peu vague et ambiguë. D’abord on suppose un spectateur au centre du Soleil ; et l’on décrit sur un plan passant par le centre de la Lune la trace réelle de ce centre et la trace apparente d’un lieu quelconque de la Terre. Ensuite on regarde cette dernière trace comme celle du lieu apparent du Soleil pour un spectateur placé sur la surface de la Terre, et l’on prend les distances mesurées sur la projection entre le lieu apparent du Soleil et le lieu réel de la Lune pour les distances ou angles apparents de ces astres pour le même spectateur, ce qui n’est pas exact, comme nous l’avons déjà observé plus haut.

11. Pour déterminer la juste valeur de $c$es distances apparentes, on considérera que, le plan de projection étant supposé perpendiculaire à la droite qui joint les centres du Soleil et de la Terre, ce plan sera, à un infiniment petit près, perpendiculaire à toutes les lignes menées des différents points de la surface de la Terre au centre du Soleil. Donc l’angle formé à un point de la surface de la Terre, par une ligne menée de ce point au centre du Soleil, et par une autre ligne menée de ce même point au centre de la Lune, aura pour tangente la distance des points d’intersectionde ces deux lignes et du plan de projection, c’est-à-dire la distance des lieux du Soleil et de la Lune, mesurée sur la projection, divisée par la distance du plan de projection même au point de la surface de la Terre dont il s’agit. Mais, comme dans les petits angles l’arc se confond avec sa tangente, que d’ailleurs les différentes lignes de la projection sont déjà exprimées en arcs dont le rayon est celui de l’orbite de la Lune, il s’ensuit que la vraie distance apparente des astres sera à la distance mesurée sur la projection, comme le rayon de l’orbite de la Lune ou la distance du centre de la Terre au plan de projection est à la distance du lieu de la surface de la Terre où est le spectateur, à ce plan. Il faut donc augmenter, dans la raison de ces dernières distances, celles qu’on aura mesurées sur la projection, pour avoir les distances apparentes cherchées, et cette augmentation est la même qui a lieu dans le diamètre apparent de la Lune, à raison de sa hauteur, et dont les astronomes ont déjà construit des Tables sous le titre d’Augmentation du diamètre ; en sorte que, après avoir mesuré les distances du Soleil et de la Lune sûr la projection, il faudra encore y appliquer une correction semblable à celle du diamètre apparent de la Lune, et dont la valeur peut aller à ${\frac {1}{60}}$ du total.

12. Il paraît que cette correction n’avait pas échappé à MM. Cassini et La Hire ; car, dans les préceptes de leurs Tables astronomiques, ils prescrivirent de diminuer la somme des demi-diamètres du Soleil et de la Lune de la quantité dont le demi-diamètre de la Lune paraît augmenté par son élévation sur l’horizon, pour pouvoir déterminer exactement sur la projection le commencement et la fin de l’éclipse. Or il est visible que c’est la même chose de diminuer la distance qu’on doit observer entre ces astres, avant de l’appliquer à la projection, que d’augmenter dans la même proportion la distance mesurée sur la projection, et de la comparer ensuite à la première distance non altérée. Cependant la plupart des astronomes qui sont venus depuis n’ont eu aucun égard à cette correction, et l’abbé de La Caille, dans le Mémoire déjà cité de 1744, dans lequel il a pris la peine de calculer la projection avec la plus grande rigueur, dit expressément (page 215) qu’il n’est pas nécessaire de diminuer la somme des demi-diamètres du Soleil et de la Lune de la quantité dont le demi-diamètre de la Lune paraît augmenté par son élévation sur l’horizon, ainsi que l’ont pratiqué MM. Cassini ét La Hire, puisqu’il ne s’agit pas ici de ce qui se passe sur une superficie sphérique, mais sur un plan. Ces dernières paroles font voir, ce me semble, que cet astronome n’avait pas une idée bien nette de la méthode des projections en tant qu’elle s’applique à la théorie des éclipses.

M. de Lalande en parle seulement dans la deuxième édition de son Astronomie, et il prétend qu’il faut appliquer au diamètre du Soleil l’augmentation de celui de la Lune a diverses hauteurs, par la raison, dit-il, que si le demi-diamètre de la Lune paraît plus grand, l’arc total de la projections $\mathrm {HL}$ paraît plus grand aussi dans la même proportion ; et, si le diamètre du Soléil était augmenté de même, il ne serait plus nécessaire d’avoir égard à l’augrrientation de $\mathrm {HL} \,;$ tout resterait proportionnel, la projection, les diamètres, le mouvement horaire (n^o 1867). J’avoue que je n’entends pas bien ce raisonnement. Il est vrai que, si le diamètre apparent du Soleil augmentait comme celui de la Lune, la projection n’aurait besoin d’aucune correction ; mais, de ce que le diamètre demeure invariable, il ne s’ensuit pas qu’il faille l’augmenter lorsqu’on veut l’appliquer à la projection ; on doit au contraire plutôt le diminuer dans la même proportion, car nous avons vu plus haut que la somme des demi-diamètresobservés de la Lune et du Soleil doit être diminuée dans la même proportion que le diamètre de la Lune paraît augmenté ; donc le diamètre de la Lune demeurera le même que s’il était vu du centre de la Terre, et le diamètre du Soleil sera seul diminué dans la proportion dont il s’agit.

M. de Lalande remarque ensuite avec raison (n^o 1874) que la méthode des projections suppose que la parallaxe de la Lune est proportionnelle au cosinus de la vraie hauteur du Soleil sur l’horizon, au lieu qu’elle est véritablement proportionnelle au cosinus de la haute ur apparente de la Lune, et il montre, par la considération des parallaxes, que l’on peut remédier à ce défaut dans le cas où les deux centres seraient dans le même vertical, en augmentant la distance apparente des centres, donnée par la projection, à raison de la hauteur de la Lune sur l’horizon. Or nous avons fait voir, en général, que cette correction a lieu également pour toutes les distances des centres, mais à raison de la hauteur du Soleil sur l’horizon.

Feu M. Lambert est celui qui paraît avoir le mieux reconnu cette aberration de la méthode ordinaire des projections, et fait sentir la nécessité d’y remédier en appliquant à toutes les distances observées des centres du Soleil et de la Lune, avant de les comparer aux distances mesurées sur la projection, une correction semblable à celle que MM. Cassini et La Hire avaient proposée seulement pour le demi-diamètre de la pénombre.

M. Lambert en a donné un exemple en calculant quelques observations des distances d’Aldébaran à différentes taches de la Lune dans les Éphémérides de 1777, et M. Schulze l’a employée depuis avec succès pour éclaircir quelques difficultés relatives à une éclipse de Soleil observée à la Chine par le P. Hellerstein. (Voir les Éphémérides de 1776 et 1778.)

13. Quoique la réduction que nous avons proposé ci-dessus de faire aux distances des centres mesurés sur la projection (11) suffise pour donner à la méthode des projections toute la rigueur qu’on peut désirer, et une rigueur égale à celle qui résulte de la méthode des parallaxes, à une seule circonstance près dont nous parlerons plus bas (n^o 18), il faut cependant convenir que, si l’on était obligé d’employer le calcul pour cette réduction, on perdrait un des avantages les plus précieux de la méthode dont il s’agit, celui de pouvoir déterminer toutes les circonstances d’une éclipse par de simples opérations graphiques et par le moyen de la règle et du compas. Cette considération m’a engagé à examiner s’il n’y aurait pas moyen de déduire la correction proposée de la projection même, ou plutôt de la faire entrer dans la construction de la projection, et je vais présenter aux astronomesles résultats de mes recherches sur ce sujet.

14. Je considérerai d’abord la projection telle qu’on l’emploie communément, et, pour n’y rien laisser à désirer du côté de l’exactitude, j’y aurai aussi égard à l’aplatissement de la Terre, ce que personne, ce me semble, n’avait encore fait.

Soit donc $\mathrm {ABD}$ le demi-cercle de projection, dans lequel le rayon $\mathrm {DC} ,$ perpendiculaire au diamètre $\mathrm {AB} ,$ représente le méridien universel. On prendra d’abord l’arc $\mathrm {DP}$ égal à la déclinaison du Soleil au temps de la conjonction ; ensuite, étant donnée la latitude du lieu dont on veut décrire le parallèle, on ajoutera à cette latitude la valeur correspondante de l’angle de la verticale avec le rayon du sphéroïde, angle dont il y a une Table à la page 164 de la troisième Partie du Recueil des Tables astronomiques de l’Académie de Berlin, pour avoir l’angle du rayon du sphéroïde de la Terre passant par le lieu donné, avec le plan de l’équateur. On prendra sur la circonférence de la projection, de part et d’autre du point $\mathrm {P} ,$ des arcs $\mathrm {PE,PF} ,$ chacun égaux à ce dernier angle, et l’on tirera la corde $\mathrm {EF}$ et les perpendiculaires $\mathrm {EG,FH}$ au rayon $\mathrm {CD} .$ Ces perpendiculaires intercepteront la partie $\mathrm {GH}$ qui sera le petit axe

demi-cercle représentant l’hémisphère nord et quelques parallèles + une visée céleste

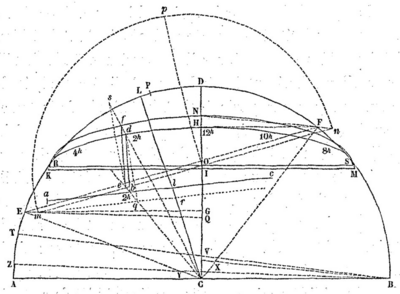
de l’ellipse, et le grand axe sera égal à la corde $\mathrm {EF} \,;$ ainsi, ayant divisé la ligne $\mathrm {GH}$ en deux parties égales au point $\mathrm {I} ,$ on y mènera par $\mathrm {I}$ une perpendiculaire $\mathrm {KIM} ,$ qu’on fera égale à la corde $\mathrm {EF} ,$ en sorte que le point $\mathrm {I}$ se trouve au milieu de la droite $\mathrm {KIM} .$ On aura ainsi les deux axes $\mathrm {GH}$ et $\mathrm {KM}$ de l’ellipse qui sera la projection orthographique du parallèle du lieu proposé. On décrira cette ellipse par les méthodes ordinaires, et on la divisera en heures et minutes suivant les règles connues, en plaçant midi au sommet du petit axe, et comptant les heures de la droite à la gauche. Lorsque la déclinaison du Soleil est septentrionale, c’est la partie inférieure de l’ellipse qui doit servir ; au contraire, ce sera la partie supérieure si la déclinaison du Soleil est méridionale. Nous avons supposé ce dernier cas dans la figure, et en conséquence nous n’avons tracé que la demi-ellipse supérieure $\mathrm {K} d\mathrm {HM} .$

On tirera maintenant le rayon $\mathrm {CL}$ qui doit représenter le cercle de latitude, et qui doit faire avec $\mathrm {DC}$ l’angle $\mathrm {LCD}$ égal à l’angle de position du Soleil. On prendra donc sur la circonférence de la projection l’arc $\mathrm {DL}$ égal à l’angle dont il s’agit, et l’on placera le point $\mathrm {L}$ à la gauche ou à l’orient de $\mathrm {D}$ lorsque le Soleil sera dans les signes descendants, et à la droite ou à l’occident lorsqu’il sera dans les signes ascendants. Ensuite, supposant le rayon de la projection $\mathrm {CB}$ égal à la parallaxe horizontale de la Lune pour la latitude proposée moins celle du Soleil (dans l’endroit cité des Tables astronomiques il y a aussi une Table de réduction pour les parallaxes horizontales de la Lune à différentes latitudes), on prendra sur ce rayon une partie égale à la latitude de la Lune, qu’on portera sur le rayon $\mathrm {CL}$ en $\mathrm {C} l\,;$ on tirera par $l$ une perpendiculaire à $\mathrm {C} l,$ sur laquelle on prendra à la gauche de $\mathrm {C} l$ une partie égale au mouvement horaire de la Lune sur l’écliptique moins celui du Soleil, et au bout de cette partie on élèvera une perpendiculaire parallèle à $\mathrm {C} l,$ sur laquelle on prendra une partie égale au mouvement horaire de la Lune en latitude, en plaçant cette partie au-dessus ou au-dessous de la ligne du mouvement horaire en longitude, suivant que la Lune s’approchera du nord ou du midi ; on mènera enfin par l’extrémité de cette ligne du mouvement en latitude, que je suppose aboutir en $a,$ et par le point $l$ la droite $alc$ qui représentera l’orbite de la Lune, et la partie $al$ sera l’espace parcouru par la Lune pendant une heure, en sorte que, marquant au point $l$ l’heure et la minute de la conjonction au méridien donné, on pourra diviser toute la partie de l’orbite qui est comprise dans la projection en heures et minutes de temps.

15. Jusqu’ici c’est la projection ordinaire dans laquelle, pour avoir égard à l’aplatissement de la Terre, nous avons supposé que la Terre est un globe dont le rayon est égal à la distance du lieu proposé, pour lequel on fait la projection, au centre de la Terre, mesurée sur le sphéroïde aplati ; car il est évident que le parallèle de ce lieu est alors le même sur ce globe que sur le sphéroïde, et qu’ainsi la projection de ce parallèle doit se faire de la même manière que si la Terre était effectivement sphérique.

Si l’on veut maintenant avoir la distance apparente des centres du Soleil et de la Lune dans un temps quelconque, comme à $2$ heures après midi, on tirera par les points $d$ et $b$ du parallèle et de l’orbite, qui répondent à $2$ heures, la ligne $db,$ et l’on portera la longueur de cette ligne sur les divisions du rayon de la projection $\mathrm {CB} \,;$ on aura ainsi la distance cherchée exprimée en minutes et même en secondes de degré, si le rayon de la projection est assez grand pour cela. Mais cette distance, pour être exacte, demande encore à être corrigée par la règle du n^o 11, laquelle consiste en ce qu’il faut augmenter la distance dont il s’agit, dans la raison de la distance du centre de la Terre au plan de projection à la distance du lieu donné sur la surface de la Terre à ce même plan. Si donc on tire par les points $d$ et $b$ au centre $\mathrm {C}$ les rayons $\mathrm {C} d,\mathrm {C} b,$ et que sur le rayon $\mathrm {C} d$ prolongé on prenne la partie $\mathrm {C} f$ qui soit à $\mathrm {C} d$ dans la raison des distances dont il s’agit ; qu’ensuite on mène par $f$ la ligne $fe$ parallèle à $db\,:$ il est clair que la partie $fe,$ interceptée entre les rayons $f\mathrm {C}$ et $e\mathrm {C} ,$ sera la distance apparente corrigée, qui, étant ensuite portée sur les divisions du rayon $\mathrm {CB} ,$ donnera la vraie distance apparente cherchée des centres du Soleil et de la Lune.

16. Tout se réduit donc à déterminer sur chaque rayon $\mathrm {C} d$ de l’ellipse $\mathrm {K} d\mathrm {HM}$ le point $f,$ en sorte que les parties $f\mathrm {C}$ et $d\mathrm {C}$ soient dans la proportion de la distance du centre de la Terre au plan de projection à la distance du lieu de la surface de la Terre, dont $d$ est la projection orthographique, au même plan. Or je dis que tous ces points $f,$ ainsi déterminés, sont aussi sur une ellipse telle que $\mathrm {R} f\mathrm {NS} ,$ laquelle est la projection du même parallèle dont $\mathrm {KHM}$ est la projection orthographique, mais pour un spectateur placé au point $\mathrm {C}$ du plan de projection, et qui rapporterait les points de la surface de la Terre à un plan passant par son centre, et parallèle au même plan de projection. En effet, il est clair que la projection orthographique de la surface de la Terre sur ce nouveau plan de projection passant par son centre sera la même que sur le plan $\mathrm {ADB}$ qui est censé toucher l’orbe de la Lune ; de sorte qu’on peut imaginer que le plan $\mathrm {ADB}$ soit celui du disque éclairé de la Terre, et que le lieu de l’œil réponde perpendiculairement au centre $\mathrm {C} ,$ à une distance de ce centre qui soit au rayon $\mathrm {CB}$ comme le rayon de l’orbite de la Lune, ou la distance du plan de projection dans l’orbe de la Lune au centre de la Terre est au rayon même de la Terre. Si donc on cherche par rapport à ce lieu de l’oeil la projection d’un point quelconque de la surface de la Terre qui réponde perpendiculairement au point $d,$ c’est-à-dire qui ait $d$ pour sa projection orthographique, il est d’abord visible que la projection dont il s’agit sera sur le même rayon $\mathrm {C} d$ qui passe par la projection orthographique ; ensuite on aura, par les règles ordinaires de la perspective, cette proportion : comme la distance de l’œil moins celle de l’objet au plan, ainsi la distance $\mathrm {C} d$ à la distance $\mathrm {C} f,$ et le point $f$ sera la projection cherchée. Or cette proportion est la même que celle par laquelle nous avons déjà déterminé ci-dessus le point $f\,;$ donc, etc. Ainsi, pour déterminer tous les points $f$ qui doivent répondre à tous les points du parallèle terrestre dont l’ellipse $\mathrm {KHM}$ est la projection orthographique, il n’y aura qu’à chercher la projection du même parallèle par-rapport à un œil placé perpendiculairement au-dessus du centre $\mathrm {C}$ et à une distance de ce centre qui soit au rayon $\mathrm {CB}$ comme la distance de la Lune à la Terre est au rayon de la Terre, et l’on doit voir d’abord par là que la projection cherchée sera aussi une ellipse dont le petit axe sera placé sur le même rayon $\mathrm {CD} \,;$ car cette projection n’est autre chose que la section d’un cône oblique dont la base est le parallèle terrestre et le sommet est le lieu de l’œil, tandis que la projection orthographique est la section faite par le même plan d’un cylindre oblique ayant la même base et le même axe que le cône.

17. Voyons maintenant comment on doit décrire la nouvelle ellipse dont il s’agit.

Je prends sur la circonférence de la projection, et du même côté du point $\mathrm {P} ,$ lorsque la déclinaison du Soleil est méridionale, ainsi qu’on le suppose dans la figure, l’arc $\mathrm {AT}$ égal au double de la parallaxe horizontale de la Lune,(il faudrait prendre cet arc de l’autre côté du point $\mathrm {P} ,$ c’est-à-dire de $\mathrm {B}$ en $\mathrm {D} ,$ si la déclinaison du Soleil était septentrionale), et je tire la corde $\mathrm {TB} \,:$ cette corde coupera le rayon $\mathrm {CD}$ en $\mathrm {V} ,$ en sorte que $\mathrm {CB}$ à $\mathrm {CV}$ aura la même proportion que la distance de la Lune à la Terre au rayon de la Terre, à cause que l’angle $\mathrm {CBV}$ est égal à la parallaxe horizontale de la Lune. Ayant tiré maintenant aux points $\mathrm {E}$ et $\mathrm {F}$ de la corde $\mathrm {EF}$ les rayons $\mathrm {CE}$ et $\mathrm {CF} ,$ on prendra sur ces rayons les parties $\mathrm {CY}$ et $\mathrm {CX}$ égales chacune à $\mathrm {CV} ,$ et l’on mènera par $\mathrm {B}$ les lignes $\mathrm {BYZ} ,$ $\mathrm {BX} \,;$ ensuite de quoi on mènera par $\mathrm {E}$ la ligne $\mathrm {EQ}$ parallèle à $\mathrm {ZB} ,$ et par $\mathrm {F}$ la ligne $\mathrm {FN}$ parallèle à $\mathrm {XB} .$ Ces deux lignes intercepteront sur le rayon $\mathrm {CD}$ la partie $\mathrm {QN} ,$ qui sera le petit axe de la nouvelle ellipse, et qu’on divisera en deux parties égales au point $\mathrm {O} ,$ pour avoir le centre de l’ellipse. Pour avoir ensuite le grand axe de l’ellipse, on mènera par $\mathrm {O}$ la ligne $mn$ parallèle à la corde $\mathrm {EF} ,$ et sur la partie $mn$ de cette ligne interceptée entre les lignes $\mathrm {EQ}$ et $\mathrm {FN} ,$ on décrira le demi-cercle $mpn\,;$ l’ordonnée rectangle $\mathrm {O} p,$ correspondante au point $\mathrm {O}$ du diamètre de ce cercle, sera le demi-grand axe cherché, qu’on portera donc en $\mathrm {OR}$ et $\mathrm {OS} ,$ sur la perpendiculaire $\mathrm {ROS}$ au rayon $\mathrm {CD} .$ Ayant ainsi le petit axe $\mathrm {QN}$ et le grand axe $\mathrm {RS} ,$ on décrira l’ellipse $\mathrm {R} f\mathrm {NS} ,$ qui sera le lieu de tous les points $f,$ et qui servira, par conséquent, à corriger les distances apparentes des deux astres pour tous les lieux de la Terre situés sur le parallèle dont $\mathrm {KHM}$ est la projection orthographique, ainsi que nous l’avons montré plus haut.

Pour démontrer cette construction, il suffira de considérer que les deux lignes $\mathrm {EQ}$ et $\mathrm {NF} ,$ étant prolongées à la droite, concourent nécessairement à un point du diamètre $\mathrm {ACB}$ prolongé vers $\mathrm {B} ,$ et que la distance de ce point de concours au centre $\mathrm {C}$ sera au rayon $\mathrm {CB}$ comme la distance de la Lune à la Terre est au rayon de la Terre ; en sorte que ce point de concours sera le lieu de l’œil pour la projection $\mathrm {ADB} .$ Le reste est analogue aux procédés de la construction orthographique, et dépend de raisonnements semblables.

18. Nous avons dit qu’il fallait diviser le rayon de la projection $\mathrm {CB}$ en autant de minutes et de secondes, si l’on veut porter la précision jusque-là, qu’en contient la différence des parallaxes horizontales de la Lune et du Soleil pour la latitude du parallèle terrestre que l’on a décrit. Or la parallaxe horizontale de la Lune étant différente pour chaque latitude dans le sphéroïde aplati, il faudra faire pour chaque parallèle qu’on voudrait décrire dans la projection une division différente du rayon $\mathrm {CB} ,$ d’où résultera un changement dans la projection et dans la division de l’orbite de la Lune alc. Voici donc comment on pourra remédier à cet inconvénient, et faire servir la même construction pour toutes les latitudes.

Supposons que le rayon $\mathrm {CB}$ soit déjà divisé, et la route $alc$ de la Lune déjà tracée pour une première latitude, et qu’on ait ensuite décrit les deux projections $\mathrm {KHM,RNS}$ d’un parallèle qui ait une autre latitude ; on prendra sur la ligne $\mathrm {C} l$ la partie $\mathrm {C} r,$ telle que $\mathrm {C} r$ soit à $\mathrm {C} l$ comme la différence des parallaxes de la Lune et du Soleil pour la première latitude est à la différence des parallaxes pour la nouvelle latitude, et l’on tirera $qr$ parallèle à $lc.$

Ensuite, tout le reste de la construction demeurant le même qu’auparavant, pour avoir la distance apparente des centres, à $2$ heures, par exemple, on tirera par le point $d$ de l’ellipse et par le point $q,$ qui est l’intersection du rayon $\mathrm {C} b$ et de la droite $qr,$ la ligne $dq,$ et par le point $e$ on tirera la ligne $es$ parallèle à $dq\,;$ la partie $es$ interceptée entre les deux rayons $cb,cd$ prolongés, s’il est nécessaire, sera la distance apparente cherchée en parties de la première division de $\mathrm {CB} ,$ ce qui est facile à démontrer. Au reste, on pourra le plus souvent négliger cette correction et prendre immédiatement $fe$ pour la distance apparente.

1. Lu à l’Académie de Berlin, le 20 janvier 1778, et imprimé en allemand dans les Éphémérides de Berlin de 1781.