Théorie mathématique de la lumière/1/Chap.06

Henri Poincaré

Théorie mathématique de la lumière

Georges Carré, 1889 (1, p. 217-318).

CHAPITRE VI

DOUBLE RÉFRACTION

144. — Le phénomène de la double réfraction, observé pour la première fois vers le milieu du xvii^e siècle dans le spath d’Islande, fut ensuite reconnu dans toutes les substances cristallisées n’appartenant pas au système cubique. Biot, qui étudia tout particulièrement la double réfraction au point de vue expérimental, divisa les cristaux biréfringents en deux classes, suivant que les phénomènes étaient symétriques tout autour d’une droite ou qu’ils semblaient se coordonner par rapport à deux droites. Les cristaux du premier groupe (cristaux uniaxes) appartiennent à l’un des systèmes cristallins rhomboédrique, hexagonal, quadratique qui possèdent un axe de symétrie cristallographique d’ordre supérieur à 2 ; cet axe de symétrie se confond avec l’axe optique du cristal. Les cristaux du second groupe (cristaux biaxes) sont orthorhombiques, clinorhombiques ou anorthiques ; les directions de leurs axes optiques ne sont pas en relation immédiate avec les éléments de symétrie de l’édifice cristallin. C’est Haüy qui, le premier, fit remarquer ces importantes relations entre la forme cristalline et la propriété biréfringente.

Les premières recherches théoriques entreprises dans le but d’expliquer la marche de la lumière dans les milieux biréfringents sont dues à Huyghens ; elles ne s’appliquaient qu’aux cristaux uniaxes. Elles furent reprises par Young, mais ce dernier, pas plus que Huyghens, ne parvint à une véritable explication du phénomène. C’est à Fresnel qu’était réservée la gloire de trouver l’explication mathématique des lois de la double réfraction dans les cristaux uniaxes et biaxes.

Les travaux de Fresnel ouvraient une voie nouvelle aux recherches des mathématiciens. Cauchy, Lamé, Neumann, Mac-Cullagh et tout récemment MM. Sarrau et Boussinesq, partant de considérations différentes, édifièrent un certain nombre de nouvelles théories.

Nous étudierons successivement ces diverses théories. Auparavant, nous déduirons des équations des petits mouvements dans un milieu élastique, l’existence d’une surface du second degré qui joue un rôle capital dans cette étude et dont l’introduction dans la science est due à Cauchy ; nous voulons parler de l’ellipsoïde de polarisation.

145. — Transformation des équations du mouvement. — Par un choix convenable de l’unité de masse, la densité $\rho$ d’une molécule d’un milieu élastique peut devenir égale à 1. Dans ces conditions, les équations générales du mouvement établies au n^o 32 deviennent

(1)

${\begin{aligned}{\frac {d^{2}\xi }{dt^{2}}}&=-\sum {\frac {d}{dx}}\cdot {\frac {d\mathrm {W} _{2}}{d\xi '_{x}}}\\[1.5ex]{\frac {d^{2}\eta }{dt^{2}}}&=-\sum {\frac {d}{dx}}\cdot {\frac {d\mathrm {W} _{2}}{d\eta '_{x}}}\\[1.5ex]{\frac {d^{2}\zeta }{dt^{2}}}&=-\sum {\frac {d}{dx}}\cdot {\frac {d\mathrm {W} _{2}}{d\zeta '_{x}}}\cdot \\\end{aligned}}$

Cherchons à satisfaire à ces équations par les valeurs de $\xi ,\,\eta ,\,\zeta$ de la forme,

(2)

${\begin{aligned}\xi &=\mathrm {A} e^{\mathrm {P} },&\eta &=\mathrm {B} e^{\mathrm {P} },&\zeta &=\mathrm {C} e^{\mathrm {P} }.\end{aligned}}$

où l’on a,

$\mathrm {P} ={\frac {2i\pi }{\lambda }}(\alpha x+\beta y+\gamma z-\mathrm {V} t).$

Nous aurons ainsi un mouvement se propageant par ondes planes normales à la droite ayant pour cosinus directeurs $\alpha ,\,\beta ,\,\gamma .$ En remplaçant dans les équations du mouvement les dérivées partielles de $\xi ,\,\eta ,\,\zeta ,$ par leurs valeurs tirées des égalités (2), on obtiendra trois équations de condition entre les quantités $\mathrm {A} ,$ $\mathrm {B} ,$ $\mathrm {C}$ et la vitesse de propagation $\mathrm {V}$ du mouvement. Il est possible de mettre ces équations sous une forme simple.

Les dérivées partielles du premier ordre de $\xi ,\,\eta ,\,\zeta ,$ par rapport aux coordonnées $x,\,y,\,z$ contiennent toutes en facteur la quantité ${\frac {2i\pi }{\lambda }}e^{\mathrm {P} }.$ Ainsi, on a

$\xi '_{x}={\frac {2i\pi }{\lambda }}\alpha \mathrm {A} e^{\mathrm {P} },\qquad \quad \xi '_{y}={\frac {2i\pi }{\lambda }}\beta \mathrm {A} e^{\mathrm {P} },\,\dots$

Par conséquent $\mathrm {W} _{2}$, qui est une fonction homogène du second degré de ces dérivées partielles, contiendra en facteur $\left({\frac {2i\pi }{\lambda }}\right)^{2}e^{2\mathrm {P} }.$ Si donc nous posons,

$\mathrm {W} _{2}=-{\frac {1}{2}}\left({\frac {2i\pi }{\lambda }}\right)^{2}e^{2\mathrm {P} }\Pi ,$

$\Pi$ sera un polynôme homogène et du second degré par rapport à $\mathrm {A} ,$ $\mathrm {B} ,$ $\mathrm {C}$ et par rapport à $\alpha ,\,\beta ,\,\gamma .$

En dérivant par rapport à $\mathrm {A}$ cette fonction $\mathrm {W} _{2}$, nous obtiendrons,

(3)

${\frac {d\mathrm {W} _{2}}{d\mathrm {A} }}=-{\frac {1}{2}}\left({\frac {2i\pi }{\lambda }}\right)^{2}e^{2\mathrm {P} }{\frac {d\Pi }{d\mathrm {A} }}\cdot$

D’ailleurs la dérivée de $\mathrm {W} _{2}$ par rapport à $\mathrm {A}$ peut s’écrire,

${\frac {d\mathrm {W} _{2}}{d\mathrm {A} }}=\sum {\frac {d\mathrm {W} _{2}}{d\xi '_{x}}}{\frac {d\xi '_{x}}{d\mathrm {A} }}\,;$

et, en remplaçant dans cette expression les dérivées par rapport à $\mathrm {A}$ des diverses dérivées partielles de $\xi ,\,\eta ,\,\zeta$ par leurs valeurs, nous aurons,

${\frac {d\mathrm {W} _{2}}{d\mathrm {A} }}={\frac {2i\pi }{\lambda }}e^{\mathrm {P} }\sum \alpha \,{\frac {d\mathrm {W} _{2}}{d\xi '_{x}}}\cdot$

En égalant cette valeur de ${\frac {d\mathrm {W} _{2}}{d\mathrm {A} }}$ à la valeur (3), et supprimant le facteur ${\frac {2i\pi }{\lambda }}e^{\mathrm {P} }$ commun aux deux membres de l’égalité obtenue, il restera,

(4)

$\sum \alpha \,{\frac {d\mathrm {W} _{2}}{d\xi '_{x}}}=-{\frac {1}{2}}{\frac {2i\pi }{\lambda }}e^{\mathrm {P} }{\frac {d\Pi }{d\mathrm {A} }}\cdot$

De cette égalité nous allons déduire une nouvelle expression du second membre des équations (1) du mouvement. La dérivée ${\frac {d\mathrm {W} _{2}}{d\xi '_{x}}}$ est une fonction homogène et linéaire par rapport aux dérivées partielles des $\xi \,;$ si donc on y remplace ces dérivées partielles par leurs valeurs tirées des relations (2), on aura en facteur la quantité ${\frac {2i\pi }{\lambda }}e^{\mathrm {P.} }$ Nous pouvons alors poser

${\frac {d\mathrm {W} _{2}}{d\xi '_{x}}}={\frac {2i\pi }{\lambda }}e^{\mathrm {P} }\varphi ,$

$\varphi$ étant une fonction homogène et linéaire par rapport à $\mathrm {A,\,B,\,C}$

et à $\alpha ,\,\beta ,\,\gamma ,$ mais ne dépendant pas de $x,\,y,\,z.$ Par conséquent

nous aurons

${\frac {d}{dx}}{\frac {d\mathrm {W} _{2}}{d\xi '_{x}}}={\frac {2i\pi }{\lambda }}e^{\mathrm {P} }\varphi \,{\frac {d\mathrm {P} }{dx}}={\frac {2i\pi }{\lambda }}e^{\mathrm {P} }\varphi \times {\frac {2i\pi \alpha }{\lambda }},$

ou

${\frac {d}{dx}}{\frac {d\mathrm {W} _{2}}{d\xi '_{x}}}={\frac {2i\pi }{\lambda }}\alpha \,{\frac {d\mathrm {W} _{2}}{d\xi '_{x}}}\,;$

et par suite

$\sum {\frac {d}{dx}}{\frac {d\mathrm {W} _{2}}{d\xi '_{x}}}={\frac {2i\pi }{\lambda }}\sum \alpha {\frac {d\mathrm {W} _{2}}{d\xi '_{x}}}\cdot$

En remplaçant dans le second membre de cette expression la quantité placée sous le signe $\textstyle \sum$ par sa valeur (4), nous obtenons,

$\sum {\frac {d}{dx}}{\frac {d\mathrm {W} _{2}}{d\xi '_{x}}}=-{\frac {1}{2}}\left({\frac {2i\pi }{\lambda }}\right)^{2}e^{\mathrm {P} }\,{\frac {d\Pi }{d\mathrm {A} }}\,;$

c’est, au signe près, la valeur du second membre de la première des équations (1).

D’autre part, la première des égalités (2) nous donne,

${\frac {d^{2}\xi }{dt^{2}}}=\mathrm {A} e^{\mathrm {P} }\mathrm {V} ^{2}\left({\frac {2i\pi }{\lambda }}\right)^{2}\,;$

par conséquent la première des équations du mouvement conduit à l’équation,

$\mathrm {A} e^{\mathrm {P} }\mathrm {V} ^{2}\left({\frac {2i\pi }{\lambda }}\right)^{2}={\frac {1}{2}}\left({\frac {2i\pi }{\lambda }}\right)^{2}e^{\mathrm {P} }{\frac {d\Pi }{d\mathrm {A} }},$

ou,

$\mathrm {AV} ^{2}={\frac {1}{2}}{\frac {d\Pi }{d\mathrm {A} }}\cdot$

Les deux autres équations du mouvement nous donneraient des équations analogues ; par suite les équations (1) peuvent être remplacées par le groupe,

(5)

${\begin{aligned}\mathrm {AV} ^{2}&={\frac {1}{2}}{\frac {d\Pi }{d\mathrm {A} }}\\[1.25ex]\mathrm {BV} ^{2}&={\frac {1}{2}}{\frac {d\Pi }{d\mathrm {B} }}\\[1.25ex]\mathrm {CV} ^{2}&={\frac {1}{2}}{\frac {d\Pi }{d\mathrm {C} }}\cdot \\\end{aligned}}$

On pourrait résoudre analytiquement le système des trois équations précédentes ; on obtiendrait les valeurs de $\mathrm {V}$ et de $\mathrm {A} ,$ $\mathrm {B} ,$ $\mathrm {C}$ qui, pour des valeurs données de $\alpha ,$ $\beta ,$ $\gamma ,$ donnent des déplacements $\xi ,\,\eta ,\,\zeta$ satisfaisant aux équations du mouvement. On peut également suivre la méthode géométrique indiquée par Cauchy ; c’est cette marche que nous adopterons.

146. Ellipsoïde de polarisation. — Si nous considérons $\mathrm {A,\,B,\,C}$ comme les coordonnées d’un point, l’équation $\Pi =1,$ dont le premier membre est homogène et du second degré par rapport à $\mathrm {A,\,B,\,C} ,$ représente une surface du second degré rapportée à son centre ; c’est l’ellipsoïde de polarisation.

Les coordonnées $\mathrm {A,\,B,\,C}$ de l’extrémité d’un axe de cette surface s’obtiendront en écrivant qu’en ce point le rayon vecteur est normal à la surface. Les cosinus directeurs de la normale étant proportionnels à ${\frac {d\Pi }{d\mathrm {A} }},$ ${\frac {d\Pi }{d\mathrm {B} }},$ ${\frac {d\Pi }{d\mathrm {C} }},$ et ceux du rayon vecteur au point $\mathrm {A,\,B,\,C} ,$ proportionnels aux coordonnées de ce point, $\mathrm {A,\,B,\,C}$ devront satisfaire aux équations,

(6)

${\begin{aligned}\mathrm {AS} &={\frac {1}{2}}{\frac {d\Pi }{d\mathrm {A} }}\\[1.25ex]\mathrm {BS} &={\frac {1}{2}}{\frac {d\Pi }{d\mathrm {B} }}\\[1.25ex]\mathrm {CS} &={\frac {1}{2}}{\frac {d\Pi }{d\mathrm {C} }}\cdot \\\end{aligned}}$

L’élimination de $\mathrm {A,B,C} ,$ entre ces trois équations, qui sont linéaires et homogènes par rapport à ces quantités, conduit, comme on le sait, à une équation en $\mathrm {S}$ du troisième degré. À chacune des racines de cette équation correspond un système de valeurs de $\mathrm {A,B,C} ,$ obtenu en portant la valeur de $\mathrm {S}$ dans les équations (6). Or ces équations ne diffèrent des équations (5) qu’en ce que $\mathrm {V} ^{2}$ a été remplacé par $\mathrm {S} .$ Par conséquent la résolution des équations (5) nous conduirait à trois valeurs de $\mathrm {V}$ et à trois systèmes de valeurs de $\mathrm {A,B,C} .$ En portant ces valeurs dans les égalités (2), nous obtiendrions trois systèmes de valeurs de $\xi ,\,\eta ,\,\zeta ,$ satisfaisant aux équations du mouvement.

Les valeurs de $\xi ,\,\eta ,\,\zeta ,$ ainsi obtenues correspondent à trois directions de déplacements dont les cosinus directeurs sont proportionnels à $\xi ,\,\eta ,\,\zeta ,$ et par suite aux trois systèmes de valeurs de $\mathrm {A,B,C} .$ Ces valeurs, solutions des équations (6), sont proportionnelles aux cosinus directeurs des axes de l’ellipsoïde de polarisation : par conséquent, les directions correspondantes des déplacements sont perpendiculaires entre elles.

En résumé, la vibration est parallèle à l’un des axes de l’ellipsoïde de polarisation, et la vitesse de propagation $\mathrm {V} ={\sqrt {\mathrm {S} }}$ est inversement proportionnelle à la longueur de cet axe.

147. De ce qui précède, il résulte que, pour qu’une onde plane se propage dans un milieu élastique anisotrope, en restant plane et perpendiculaire à la même direction $\alpha ,\beta ,\gamma ,$ il faut que les déplacements des molécules du plan de l’onde soient parallèles à l’un des axes de l’ellipsoïde de polarisation. Si la vibration des molécules du plan de l’onde n’a pas lieu suivant une de ces directions, on pourra, d’après le principe de la superposition des petits mouvements, décomposer le déplacement de chaque molécule en trois composantes, suivant les axes de l’ellipsoïde, et considérer l’onde donnée comme formée de trois ondes planes, dont les vibrations seraient parallèles à ces axes. Chacune de ces ondes planes se propagera sans altération et comme leurs vitesses de propagation (les racines carrées des racines de l’équation en $\mathrm {S}$), sont en général différentes, ces ondes se sépareront. Par conséquent, d’après la théorie de l’élasticité, un rayon lumineux, traversant un milieu anisotrope, doit donner naissance à trois rayons ; on devrait avoir une triple réfraction.

Cette conséquence est en contradiction avec l’expérience qui n’a jamais révélé qu’une double réfraction. Pour mettre d’accord la théorie de l’élasticité avec l’expérience, on peut faire diverses hypothèses sur la constitution du milieu qui transmet les vibrations lumineuses.

On peut admettre :

1^o Que l’éther est incompressible (Fresnel) ;

2^o Qu’un des trois rayons prévus par la théorie n’est pas perceptible, son intensité étant trop faible (Cauchy) ;

3^o Que la vitesse de propagation suivant une direction est nulle. L’ellipsoïde de polarisation, dont les axes sont en raison inverse des vitesses, devient alors un cylindre (Lamé, Neumann, Mac-Cullagh) ;

4^o Que l’un des axes de l’ellipsoïde de polarisation, qui devient un hyperboloïde est imaginaire. Le rayon lumineux vibrant suivant la direction de cet axe est alors évanescent.

C’est là sans doute l’hypothèse à laquelle se serait arrêté Cauchy, s’il était revenu, sur la fin de sa vie, à la théorie de la double réfraction.

Par l’étude des diverses théories de la double réfraction, nous verrons que ces hypothèses fondamentales, complétées quelquefois par des hypothèses secondaires, permettent d’expliquer le phénomène de la double réfraction.

148. Dans les milieux isotropes, la réfraction de la lumière ne donne lieu qu’à un seul rayon réfracté ; cherchons ce que devient dans ce cas particulier l’ellipsoïde de polarisation.

Nous avons vu (24) que dans les milieux isotropes, la fonction $\mathrm {W} _{2}$ se réduit à

$\mathrm {W} _{2}=\lambda \mathrm {K} +\mu \mathrm {H} +\nu \Theta ^{2}.$

Le polynôme $\mathrm {K}$ disparaissant des équations du mouvement (33), nous pouvons, sans changer les résultats, supposer que $\mathrm {K}$ n’entre pas dans l’expression de $\mathrm {W} _{2}.$ Admettons donc que l’on ait $\lambda =0$ et qu’en outre, pour tenir compte de la transversalité des vibrations, $\mu$ et $\nu$ soient liées (46) par la relation,

$\mu +\nu =0.$

La fonction $\mathrm {W} _{2}$ devient alors :

$\mathrm {W_{2}=\mu (\mathrm {H} -\Theta ^{2})}$

ou, en remplaçant dans cette expression $\mathrm {H}$ et $\Theta$ par les valeurs trouvées aux n^os 19 et 20,

$\mathrm {W} _{2}=\mu \left[\sum \xi _{x}'^{2}-(\xi '_{x}+\eta '_{y}+\zeta '_{z})^{2}\right].$

On déduit facilement de cette nouvelle expression, l’équation suivante pour l’ellipsoïde de polarisation.

$\Pi =\mu \left[(\alpha ^{2}+\beta ^{2}+\gamma ^{2})(\mathrm {A} ^{2}+\mathrm {B} ^{2}+\mathrm {C} ^{2})-\left(\mathrm {A} \alpha +\mathrm {B} \beta +\mathrm {C} \gamma \right)^{2}\right]=1$

c’est l’équation d’un cylindre de révolution tangent à la sphère

$\mathrm {A} ^{2}+\mathrm {B} ^{2}+\mathrm {C} ^{2}={\frac {1}{\mu }},$

suivant la circonférence découpée dans cette sphère par le plan

$\mathrm {A} \alpha +\mathrm {B} \beta +\mathrm {C} \gamma =0.$

L’ellipsoïde de polarisation se réduisant à un cylindre de révolution, l’un des axes de cet ellipsoïde devient infini, et la vitesse de propagation correspondante, qui est l’inverse de la longueur de cet axe, devient nulle. Les deux autres axes sont égaux au rayon de la sphère. Par suite, on n’a qu’une seule valeur pour la vitesse de propagation de la lumière dans un milieu isotrope, conséquence conforme à l’expérience.

THÉORIE DE FRESNEL

149. Convaincu, par l’étude des phénomènes d’interférence de la lumière polarisée, de la transversalité des vibrations lumineuses dans l’air, Fresnel tenta en s’appuyant sur ce résultat expérimental d’expliquer les phénomènes de la double réfraction présentés par les cristaux à un axe et à deux axes. En admettant que ces vibrations transversales sont normales au plan de polarisation, il ne tarda pas à trouver une explication de la propagation de la lumière dans les uniaxes dont les conséquences s’accordaient avec les lois expérimentales connues, en particulier avec la loi de Malus. Par une suite de déductions heureuses, dont on trouve la trace dans son premier Mémoire sur la double réfraction^[1], il parvint à se rendre compte de la marche de la lumière dans les biaxes.

Ayant vérifié, par de nombreuses expériences, la conception qu’il s’était faite du phénomène de la double réfraction, Fresnel en rechercha l’explication mécanique. Il y parvint, grâce à deux hypothèses fondamentales. Nous verrons plus loin quelles sont ces hypothèses, et comment une analyse rigoureuse permet d’en déduire les véritables lois de la double réfraction. Mais d’abord nous rappellerons succinctement quelle a été la marche des idées de Fresnel, en renvoyant pour les détails aux œuvres complètes du grand physicien.

150. Explication mécanique de la double réfraction. — Si on imprime à une molécule d’un milieu élastique, des déplacements égaux dans toutes les directions, chacun d’eux donne naissance à une force élastique inversement proportionnelle à la racine carrée du rayon vecteur, dirigé suivant le déplacement, d’un certain ellipsoïde, et parallèle à la normale à l’ellipsoïde à l’extrémité de ce rayon vecteur. C’est cet ellipsoïde qu’on appelle ellipsoïde inverse d’élasticité, et souvent aussi ellipsoïde d’élasticité. Les axes de cet ellipsoïde sont donc tels qu’à un déplacement dirigé suivant l’un d’eux correspond une force élastique de même direction et de sens inverse ; ce sont les axes d’élasticité du milieu.

L’intersection de l’ellipsoïde d’élasticité par un plan sera une ellipse que nous désignerons par $\mathrm {E} \,;$ un déplacement suivant un des axes de cette ellipse donnera naissance à une force élastique qui, en général, ne sera pas dans le plan de l’ellipse $\mathrm {E} ,$ mais dont la projection sur ce plan sera dirigée suivant l’axe lui-même. Si on admet avec Fresnel que cette composante de la force élastique est seule efficace, la vibration résultant du déplacement se propagera dans le milieu en conservant la même direction. La vitesse de propagation qui est en général proportionnelle à la racine carrée de la force agissante sera proportionnelle à l’axe de l’ellipse dirigé suivant le déplacement. Dans le cas où le déplacement considéré est quelconque dans le plan de l’ellipse, on peut le regarder comme résultant de deux déplacements dirigés suivant les axes ; les axes étant inégaux, les vitesses de propagation seront différentes.

Considérons maintenant une onde plane ; nous admettrons avec Fresnel, que la force élastique développée par les vibrations des molécules de cette onde est proportionnelle à la force élastique résultant du déplacement d’une seule molécule. Si nous regardons cette onde comme résultant de la superposition de deux ondes planes ayant pour directions de vibrations les axes de l’ellipse, ces deux ondes auront d’après ce qui précède des vibrations rectangulaires et des vitesses de propagation différentes. Cette conséquence est donc conforme à l’expérience, qui montre qu’une onde plane polarisée dans un azimuth quelconque se dédouble dans un cristal biréfringent en deux ondes planes distinctes, polarisées à angle droit.

Dans le cas où le plan de l’onde incidente se confond avec une des sections cycliques de l’ellipsoïde d’élasticité, les deux vitesses de propagation sont égales, et l’onde ne se dédouble pas ; de plus l’onde émergente doit conserver son plan primitif de polarisation. Comme un ellipsoïde à trois axes inégaux possède deux séries de plans cycliques, on devra avoir en général deux directions de propagation jouissant des propriétés précédentes ; ces directions seront celles des axes optiques du cristal. Quand l’ellipsoïde d’élasticité devient de révolution, il n’y a plus qu’une série de sections cycliques, et par suite qu’un seul axe optique : c’est ce qui a lieu pour les cristaux uniaxes.

151. Hypothèses de Fresnel. — Telle est, en résumé, la théorie de Fresnel. Elle est de tous points conforme aux lois expérimentales ; mais nous voyons qu’elle repose sur deux hypothèses qui demandent à être examinées de plus près. Ces deux hypothèses peuvent s’énoncer :

1^o La force élastique développée par le mouvement d’une onde plane est indépendante de la direction du plan de l’onde, elle ne dépend que de la direction des vibrations des molécules, et elle est proportionnelle à la force élastique développée par une molécule isolée, les autres molécules du plan de l’onde restant en repos.

2^o La seule composante de la force élastique qui soit efficace est la composante parallèle au plan de l’onde.

La première de ces hypothèses, que Fresnel a vainement essayé de justifier, est entièrement arbitraire, mais rien n’empêche de l’admettre. Il suffit pour cela de supposer que l’ellipsoïde de polarisation de Cauchy est invariable et indépendant de la direction du plan de l’onde, c’est-à-dire de $\alpha ,$ $\beta$ et $\gamma .$ Cela arrivera quand le polynôme $\Pi$ se réduira à un polynôme du 2^e degré en $\mathrm {A,\,B,\,C}$ multiplié par

$\alpha ^{2}+\beta ^{2}+\gamma ^{2}=1.$

Cet ellipsoïde fixe de polarisation n’est autre chose, comme nous le verrons plus loin, que l’ellipsoïde d’élasticité de Fresnel.

Quant à la seconde, elle est une conséquence immédiate de l’incompressibilité de l’éther. Nous avons déjà dit (48) que, dans ses calculs, Fresnel admettait, souvent implicitement, tantôt que la résistance de l’éther à la compression était nulle, tantôt qu’elle était infinie. Dans ce cours, nous nous sommes placés jusqu’ici dans la première hypothèse ; cherchons maintenant quelles sont les équations du mouvement dans l’hypothèse où la résistance à la compression est infinie, c’est-à-dire dans l’hypothèse où le milieu élastique est incompressible.

152. Équations du mouvement dans un milieu incompressible. — L’incompressibilité imposée à l’éther suppose des liaisons entre ses diverses molécules ; nous devons donc appliquer la théorie des systèmes matériels à liaisons.

L’équation exprimant que l’éther est incompressible est $\Theta =0.$ Si nous considérons un certain volume $\mathrm {R}$ de l’éther limité par une surface $\mathrm {S} ,$ et si nous désignons par $\mathrm {U}$ la fonction des forces relative aux forces intérieures et extérieures à $\mathrm {R} ,$ nous arriverons, en appliquant le principe de d’Alembert et celui des vitesses virtuelles, à l’équation

$\delta \mathrm {U} -\int \rho \,d\tau \left({\frac {d^{2}\xi }{dt^{2}}}\,\delta \xi +{\frac {d^{2}\eta }{dt^{2}}}\,\delta \eta +{\frac {d^{2}\zeta }{dt^{2}}}\,\delta \zeta \right)+\int \Lambda \,\delta \Theta \,d\tau =0,$

qui, pour un choix convenable de la fonction arbitraire $\Lambda ,$ doit être satisfaite identiquement, quels que soient les déplacements virtuels $\delta \xi ,$ $\delta \eta ,$ $\delta \zeta .$ On peut donc supposer que l’on a $\delta \eta =\delta \zeta =0.$ Dans ce cas, $\delta \mathrm {U}$ peut, comme nous l’avons déjà vu (29), être remplacé par la somme

$\delta \mathrm {U} =\int \mathrm {P} _{x}\,\delta \xi \,d\omega +\int \delta \mathrm {W} \,d\tau ,$

$\mathrm {P} _{x}$ étant la composante suivant l’axe des $x$ de la pression qui s’exerce sur un élément $d\omega$ de surface $\mathrm {S} ,$ et qui résulte des actions des molécules de $\mathrm {R} '$ sur celles de $\mathrm {R} .$ L’équation précédente, en y faisant $\delta \eta =\delta \zeta =0$ et en remarquant que l’on a $\Theta =\xi '_{x}+\eta '_{y}+\zeta '_{z},$ devient alors

(1)

$\int \mathrm {P} _{x}\,\delta \xi \,d\omega +\int \delta \mathrm {W} \,d\tau -\int \rho \,{\frac {d^{2}\xi }{dt^{2}}}\,\delta \xi \,d\tau +\int \Lambda \,\delta \xi '_{x}\,d\tau =0.$

Nous devrons, comme nous l’avons fait au [[Théorie mathématique de la lumière/1/Chap.01#par030|n^o 30]], transformer les intégrales du premier membre de manière à ce qu’elles ne contiennent plus de termes en $\delta \xi '_{x}.$ Dans cette transformation nous obtiendrons des intégrales doubles étendues à la surface $\mathrm {S}$ et des intégrales triples étendues au volume $\mathrm {R} .$ Les intégrales doubles n’entrant pas dans les équations du mouvement, nous abrégerons la recherche de ces équations en n’introduisant pas ces intégrales dans nos calculs, ce qui peut se faire en supposant qu’on étend les intégrales triples à tout l’espace et qu’à l’infini les forces élastiques sont nulles.

Dans ces conditions, la première intégrale de l’équation précédente disparaît, et nous avons pour la valeur de la seconde

$\int \delta \mathrm {W} \,d\tau =-\int \delta \xi \,d\tau \sum {\frac {d}{dx}}{\frac {d\mathrm {W} }{d\xi '_{x}}}\cdot$

Quant à la dernière intégrale nous la transformerons d’une manière analogue en nous appuyant sur l’égalité connue

$\iiint {\frac {d\mathrm {F} }{dx}}\,d\tau =\iint \alpha \mathrm {F} \,d\omega ,$

et en posant

$\mathrm {F} =\Lambda \,\delta \xi .$

Nous obtiendrons

$\iiint \Lambda {\frac {d}{dx}}\delta \xi \,d\tau =\iint \alpha \Lambda \,\delta \xi \,d\omega -\iiint {\frac {d\Lambda }{dx}}\,\delta \xi \,d\tau ,$

ou, puisque d’après nos conventions l’intégrale double est nulle,

$\int \Lambda \,\delta \xi '_{x}\,d\tau =-\int {\frac {d\Lambda }{dx}}\,\delta \xi \,d\tau .$

Par conséquent l’équation (1) peut s’écrire

$\int \delta \xi \,d\tau \sum {\frac {d}{dx}}{\frac {d\mathrm {W} }{d\xi '_{x}}}+\int \rho \,{\frac {d^{2}\xi }{dt^{2}}}\,\delta \xi \,d\tau +\int {\frac {d\Lambda }{dx}}\,\delta \xi \,d\tau =0,$

ou

$\int \left(\rho \,{\frac {d^{2}\xi }{dt^{2}}}+\sum {\frac {d}{dx}}{\frac {d\mathrm {W} }{d\xi '_{x}}}+{\frac {d\Lambda }{dx}}\right)\delta \xi \,d\tau =0.$

Puisqu’elle doit être satisfaite quel que soit $\delta \xi ,$ le coefficient de cette quantité dans l’élément différentiel doit être nul. On a ainsi une des équations du mouvement. Si nous faisons $\rho =1$ et si nous remarquons que nous avons déjà trouvé (32) l’égalité

$\sum {\frac {d}{dx}}{\frac {d\mathrm {W} }{d\xi '_{x}}}=\sum {\frac {d}{dx}}{\frac {d\mathrm {W} _{2}}{d\xi '_{x}}},$

nous aurons pour les équations du mouvement

(2)

${\begin{aligned}{\frac {d^{2}\xi }{dt^{2}}}&=-\sum {\frac {d}{dx}}{\frac {d\mathrm {W} _{2}}{d\xi '_{x}}}-{\frac {d\Lambda }{dx}},\\[1.25ex]{\frac {d^{2}\eta }{dt^{2}}}&=-\sum {\frac {d}{dx}}{\frac {d\mathrm {W} _{2}}{d\eta '_{x}}}-{\frac {d\Lambda }{dy}},\\[1.25ex]{\frac {d^{2}\zeta }{dt^{2}}}&=-\sum {\frac {d}{dx}}{\frac {d\mathrm {W} _{2}}{d\zeta '_{x}}}-{\frac {d\Lambda }{dz}}\cdot \\\end{aligned}}$

153. Propagation d’une onde plane. — Considérons une onde plane parallèle au plan

$\alpha x+\beta y+\gamma z=0.$

Les composantes des déplacements des molécules de cette onde seront de la forme

$\xi =\mathrm {A} e^{\mathrm {P} },\qquad \quad \eta =\mathrm {B} e^{\mathrm {P} },\qquad \quad \zeta =\mathrm {C} e^{\mathrm {P} },$

où

$\mathrm {P} ={\frac {2i\pi }{\lambda }}\left(\alpha x+\beta y+\gamma z-\mathrm {V} t\right).$

Nous avons vu précédemment (145) que pour des valeurs de $\xi ,\,\eta ,\,\zeta$ de cette forme, on a

${\begin{aligned}\mathrm {W} _{2}&=-{\frac {1}{2}}\left({\frac {2i\pi }{\lambda }}\right)^{2}e^{2\mathrm {P} }\Pi ,\\[1.25ex]\sum {\frac {d}{dx}}{\frac {\mathrm {W} _{2}}{d\xi '_{x}}}&=-{\frac {1}{2}}\left({\frac {2i\pi }{\lambda }}\right)^{2}e^{\mathrm {P} }{\frac {d\Pi }{d\Lambda }},\\[1.25ex]{\frac {d^{2}\xi }{dt^{2}}}&=\mathrm {A} e^{\mathrm {P} }\mathrm {V} ^{2}\left({\frac {2i\pi }{\lambda }}\right)^{2}\cdot \end{aligned}}$

Nous sommes donc conduits pour satisfaire aux équations du mouvement (2), à poser

$\Lambda =\mathrm {H} \,{\frac {2i\pi }{\lambda }}\,e^{\mathrm {P} },$

$\mathrm {H}$ étant une constante indépendante de $x,$ $y,$ $z$ et $t\,;$ nous tirons de cette égalité

${\frac {d\Lambda }{dx}}=\alpha \mathrm {H} \left({\frac {2i\pi }{\lambda }}\right)^{2}e^{\mathrm {P} }.$

Si nous portons les valeurs de ces diverses quantités dans les équations (2), nous aurons en supprimant le facteur $\left({\frac {2i\pi }{\lambda }}\right)^{2}e^{\mathrm {P} }$ commun aux deux membres,

(3)

${\begin{aligned}\mathrm {AV} ^{2}&={\frac {1}{2}}{\frac {d\Pi }{d\mathrm {A} }}-\alpha \mathrm {H} ,\\[1.5ex]\mathrm {BV} ^{2}&={\frac {1}{2}}{\frac {d\Pi }{d\mathrm {B} }}-\beta \mathrm {H} ,\\[1.5ex]\mathrm {CV} ^{2}&={\frac {1}{2}}{\frac {d\Pi }{d\mathrm {C} }}-\gamma \mathrm {H} .\\\end{aligned}}$

Ces trois équations jointes à l’équation de liaison $\Theta =0$ permettront de déterminer $\mathrm {H}$ et des quantités proportionnelles à $\mathrm {A,B,C} .$ L’équation de liaison devient, quand on y remplace les dérivées partielles de $\xi ,\,\eta ,\,\zeta$ par leurs valeurs,

$\Theta ={\frac {2i\pi }{\lambda }}\,e^{\mathrm {P} }\left(\mathrm {A} \alpha +\mathrm {B} \beta +\mathrm {C} \gamma \right),$

d’où

(4)

$\mathrm {A} \alpha +\mathrm {B} \beta +\mathrm {C} \gamma =0.$

Cette équation exprime que la vibration a lieu dans le plan de l’onde ; nous devions nous attendre à cette conséquence, la transversalité des vibrations étant exprimée par l’identité $\Theta =0.$

Si l’on compare les équations de condition (3) aux équations (5) du n^o (145), on voit qu’elles ne diffèrent de celles-ci que par l’introduction des quantités $\alpha \mathrm {H} ,$ $\beta \mathrm {H} ,$ $\gamma \mathrm {H} .$ Ces quantités sont donc, à un facteur constant près, les composantes de la force de liaison ; par suite, les cosinus directeurs de cette force sont proportionnels à $\alpha ,\,\beta ,\,\gamma .$ La force de liaison est donc normale au plan de l’onde, et cette conséquence mathématique de l’incompressibilité de l’éther aurait pu remplacer la seconde des hypothèses de Fresnel.

154. Les valeurs de la vitesse de propagation de l’onde plane s’obtiendront en éliminant $\mathrm {A} ,$ $\mathrm {B} ,$ $\mathrm {C} ,$ $\mathrm {H}$ entre les équations (3) et l’équation (4). Si nous admettons avec Fresnel que la force élastique résultant du déplacement d’une onde plane, est indépendante de la direction de l’onde, la fonction des forces $\mathrm {W} _{2}$ ne doit pas dépendre de $\alpha ,\,\beta ,\,\gamma ,$ et, par suite, le polynôme $\Pi$ doit se réduire à un polynôme homogène du second degré en $\mathrm {A,\,B,\,C} ,$ multiplié par un polynôme homogène du second degré de $\alpha ,\,\beta ,\,\gamma ,$ dont la valeur est constante ; ce dernier polynôme ne peut être que $\alpha ^{2}+\beta ^{2}+\gamma ^{2}.$ En prenant les axes de coordonnées parallèles aux axes de l’ellipsoïde de polarisation $\Pi =1,$ on aura

$\Pi =(a\mathrm {A} ^{2}+b\mathrm {B} ^{2}+c\mathrm {C} ^{2})(\alpha ^{2}+\beta ^{2}+\gamma ^{2})=a\mathrm {A} ^{2}+b\mathrm {B} ^{2}+c\mathrm {C} ^{2}$

et par suite,

${\begin{aligned}{\frac {1}{2}}{\frac {d\Pi }{d\mathrm {A} }}&=a\mathrm {A} ,&{\frac {1}{2}}{\frac {d\Pi }{d\mathrm {B} }}&=b\mathrm {B} ,&{\frac {1}{2}}{\frac {d\Pi }{d\mathrm {C} }}&=c\mathrm {C} .\end{aligned}}$

En portant ces valeurs dans les équations (3) nous obtenons

(5)

${\begin{aligned}\mathrm {AV} ^{2}&={a\mathrm {A} }-\alpha \mathrm {H} ,\\[1.5ex]\mathrm {BV} ^{2}&={b\mathrm {B} }-\beta \mathrm {H} ,\\[1.5ex]\mathrm {CV} ^{2}&={c\mathrm {C} }-\gamma \mathrm {H} \,;\\\end{aligned}}$

d’où,

$\mathrm {A} =-{\frac {\alpha \mathrm {H} }{\mathrm {V} ^{2}-a}},\qquad \mathrm {B} =-{\frac {\beta \mathrm {H} }{\mathrm {V} ^{2}-b}},\qquad \mathrm {C} =-{\frac {\gamma \mathrm {H} }{\mathrm {V} ^{2}-c}}\cdot$

Si nous multiplions ces dernières égalités respectivement par $\alpha ,$ $\beta ,$ $\gamma ,$ et si nous additionnons, nous trouvons

$\mathrm {A} \alpha +\mathrm {B} \beta +\mathrm {C} \gamma =-\mathrm {H} \left({\frac {\alpha ^{2}}{\mathrm {V} ^{2}-a}}+{\frac {\beta ^{2}}{\mathrm {V} ^{2}-b}}+{\frac {\gamma ^{2}}{\mathrm {V} ^{2}-c}}\right),$

et si nous tenons compte de l’équation de condition (4), nous avons

${\frac {\alpha ^{2}}{\mathrm {V} ^{2}-a}}+{\frac {\beta ^{2}}{\mathrm {V} ^{2}-b}}+{\frac {\gamma ^{2}}{\mathrm {V} ^{2}-c}}=0.$

Cette équation déterminera $\mathrm {V}$ ; on aura donc deux valeurs pour la vitesse de propagation.

155. Il est facile de trouver une expression de $\mathrm {V}$ en fonction de $\mathrm {A,B,C.}$ Il suffit de multiplier successivement chacune des équations (5) par $\mathrm {A} ,$ $\mathrm {B}$ et $\mathrm {C}$ et d’additionner. On obtient ainsi

$\left(\mathrm {A} ^{2}+\mathrm {B} ^{2}+\mathrm {C} ^{2}\right)\mathrm {V} ^{2}=a\mathrm {A} ^{2}+b\mathrm {B} ^{2}+c\mathrm {C} ^{2}.$

Or les équations (5) jointes à l’équation (4) ne déterminent que des quantités proportionnelles à $\mathrm {A,\,B,\,C} \,;$ nous pouvons donc satisfaire à ces équations et par suite aux équations du mouvement par des valeurs de $\mathrm {A,\,B,\,C}$ satisfaisant à la relation

(6)

$\Pi =a\mathrm {A} ^{2}+b\mathrm {B} ^{2}+c\mathrm {C} ^{2}=1.$

On a alors

$\mathrm {V} ={\frac {1}{\sqrt {\mathrm {A} ^{2}+\mathrm {B} ^{2}+\mathrm {C} ^{2}}}}\cdot$

L’interprétation géométrique de cette expression est évidente ; la vitesse de propagation est inversement proportionnelle à la longueur du rayon vecteur de l’ellipsoïde $\Pi =1$ ayant pour direction celle du déplacement. Il en résulte que l’ellipsoïde

$a\mathrm {A} ^{2}+b\mathrm {B} ^{2}+c\mathrm {C} ^{2}=1$

n’est autre que l’ellipsoïde d’élasticité de Fresnel.

156. Nous terminerons l’étude de la théorie de Fresnel en faisant remarquer qu’il n’est pas nécessaire de supposer l’éther incompressible et qu’on peut arriver aux mêmes conséquences d’une autre manière. Il suffit de supposer que l’équation de l’ellipsoïde de polarisation est d’une forme particulière.

Si nous multiplions la première des équations (3) par $\alpha ,$ la seconde par $\beta ,$ la troisième par $\gamma$ et si nous additionnons, nous obtenons

$\mathrm {V} ^{2}\left(\mathrm {A} \alpha +\mathrm {B} \beta +\mathrm {C} \gamma \right)=\mathrm {A} a\alpha +\mathrm {B} b\beta +\mathrm {C} c\gamma -\mathrm {H} \,;$

et comme d’après la condition (4) le premier membre de cette relation est égal à zéro, nous en tirons

$\mathrm {H} =\mathrm {A} a\alpha +\mathrm {B} b\beta +\mathrm {C} c\gamma .$

Admettons que l’équation de l’ellipsoïde de polarisation soit

(7)

$\;\Pi =\left(a\mathrm {A} ^{2}\!+\!b\mathrm {B} ^{2}\!+\!c\mathrm {C} ^{2}\right)(\alpha ^{2}\!+\!\beta ^{2}\!+\!\gamma ^{2})-2\mathrm {H} \left(\mathrm {A} \alpha \!+\mathrm {B} \beta \!+\mathrm {C} \gamma \right)=1,$

où $\mathrm {H}$ a pour valeur l’expression précédente. En portant cette

valeur de $\Pi$ dans les équations (5) du n^o 145 déduites des équations du mouvement dans un milieu élastique non assujetti

à des liaisons, nous obtiendrons

(8)

${\begin{aligned}\mathrm {AV} ^{2}&={a\mathrm {A} }-\alpha \mathrm {H} -{\frac {d\mathrm {H} }{d\mathrm {A} }}(\mathrm {A} \alpha +\mathrm {B} \beta +\mathrm {C} \gamma ),\\[1.5ex]\mathrm {BV} ^{2}&={b\mathrm {B} }-\beta \mathrm {H} -{\frac {d\mathrm {H} }{d\mathrm {B} }}(\mathrm {A} \alpha +\mathrm {B} \beta +\mathrm {C} \gamma ),\\[1.5ex]\mathrm {CV} ^{2}&={c\mathrm {C} }-\gamma \mathrm {H} -{\frac {d\mathrm {H} }{d\mathrm {C} }}(\mathrm {A} \alpha +\mathrm {B} \beta +\mathrm {C} \gamma )\,;\\\end{aligned}}$

nous déduirons de ces équations en les multipliant respectivement par $a,\beta ,\gamma$ et additionnant les produits

${\begin{aligned}\mathrm {V} ^{2}(\mathrm {A} \alpha +\mathrm {B} \beta +\mathrm {C} \gamma )&=\mathrm {A} a\alpha +\mathrm {B} b\beta +\mathrm {C} c\gamma -(\alpha ^{2}+\beta ^{2}+\gamma ^{2})\mathrm {H} \\&\;\;-(\mathrm {A} \alpha +\mathrm {B} \beta +\mathrm {C} \gamma )\left(\alpha \,{\frac {d\mathrm {H} }{d\mathrm {A} }}+\beta \,{\frac {d\mathrm {H} }{d\mathrm {B} }}+\gamma \,{\frac {d\mathrm {H} }{d\mathrm {C} }}\right),\end{aligned}}$

ou, en remplaçant $\mathrm {H}$ par sa valeur,

$\mathrm {V} ^{2}(\mathrm {A} \alpha +\mathrm {B} \beta +\mathrm {C} \gamma )=-(\mathrm {A} \alpha +\mathrm {B} \beta +\mathrm {C} \gamma )\left(\alpha \,{\frac {d\mathrm {H} }{d\mathrm {A} }}+\beta \,{\frac {d\mathrm {H} }{d\mathrm {B} }}+\gamma \,{\frac {d\mathrm {H} }{d\mathrm {C} }}\right)\cdot$

Une solution de cette équation est

(9)

$\mathrm {A} \alpha +\mathrm {B} \beta +\mathrm {C} \gamma =0,$

équation qui est celle que nous avons déduite de la condition $\Theta =0$ exprimant l’incompressibilité. Quand cette équation est satisfaite, les équations (8) se réduisent aux équations (5). Nous retrouvons donc ainsi les équations (4) et (5) obtenues en supposant l’éther incompressible.

Une autre conséquence de l’équation (9) est que la normale au plan de l’onde est perpendiculaire aux directions de vibration satisfaisant aux équations du mouvement. Comme, d’une manière générale, ces vibrations ont pour directions les axes de l’ellipsoïde de polarisation, le plan de l’onde est un plan de symétrie de l’ellipsoïde de polarisation déterminé par l’équation (7).

THÉORIE DE CAUCHY

157. Plans de symétrie optique dans les cristaux biréfringents. — Cauchy admet que dans tout milieu anisotrope, l’éther qui s’y trouve contenu admet trois plans de symétrie rectangulaires. La forme extérieure d’un certain nombre de substances cristallisées nous montre qu’une telle symétrie existe pour les molécules matérielles dans les cristaux appartenant aux systèmes cubique, hexagonal, rhomboédrique, quaternaire ou orthorhombique ; il est donc rationnel d’admettre que dans ces substances la même symétrie se présente pour les molécules d’éther. Mais pour les cristaux des deux derniers systèmes cristallins, le système clinorhombique et le système anorthique, on n’a plus trois plans de symétrie et rien, a priori, ne nous autorise à admettre l’existence de ces trois plans dans l’éther. En réalité, l’expérience montre qu’au point de vue optique les cristaux anorthiques et clinorhombiques possèdent trois plans de symétrie ; mais ces plans, au lieu d’avoir des positions fixes par rapport aux éléments de symétrie du cristal, ont des directions variables avec la durée de la vibration, c’est-à-dire avec la longueur d’onde de la lumière. Si donc nous admettons, avec Cauchy, l’existence de trois plans de symétrie rectangulaires dans tout milieu anisotrope nous devrons toujours supposer la lumière homogène et nous négligerons ainsi les phénomènes dus à la dispersion, comme nous l’avons fait dans l’étude de la théorie de Fresnel, où les plans principaux de l’ellipsoïde d’élasticité n’étaient autres que les plans de symétrie optique.

Nous choisirons ces trois plans de symétrie comme plans de coordonnées. Par raison de symétrie, le premier membre $\Pi$ de l’équation de l’ellipsoïde de polarisation ne doit pas changer quand on y fait $\alpha =-\alpha$ et $\mathrm {A} =-\mathrm {A} ,$ ou $\beta =-\beta$ et $\mathrm {B} =-\mathrm {B} ,$ ou enfin $\gamma =-\gamma$ et $\mathrm {C} =-\mathrm {C} .$ Il en résulte que $\Pi$ ne doit contenir que des termes de la forme suivante,

${\begin{array}{llll}\alpha ^{2}\mathrm {A} ^{2},\qquad &\beta ^{2}\mathrm {A} ^{2},\qquad &\gamma ^{2}\mathrm {A} ^{2},\qquad &\beta \gamma \mathrm {BC} ,\\[1.5ex]\alpha ^{2}\mathrm {B} ^{2},\qquad &\beta ^{2}\mathrm {B} ^{2},\qquad &\gamma ^{2}\mathrm {B} ^{2},\qquad &\alpha \gamma \mathrm {AC} ,\\[1.5ex]\alpha ^{2}\mathrm {C} ^{2},\qquad &\beta ^{2}\mathrm {C} ^{2},\qquad &\gamma ^{2}\mathrm {C} ^{2},\qquad &\alpha \beta \mathrm {AB} .\end{array}}$

Le nombre de ces termes étant égal à 12, $\Pi$ pourra contenir 12 coefficients numériques arbitraires et l’équation de l’ellipsoïde de polarisation sera de la forme

(1)

${\begin{aligned}\;\mathrm {A} ^{2}(\lambda \alpha ^{2}+\mu \beta ^{2}+\nu \gamma ^{2})&+\mathrm {B} ^{2}(\lambda '\alpha ^{2}+\mu '\beta ^{2}+\nu '\gamma ^{2})\\[1ex]+\mathrm {C} ^{2}(\lambda ''\alpha ^{2}+\mu ''\beta ^{2}+\nu ''\gamma ^{2})&+2p\beta \gamma \mathrm {BC} +2q\gamma \alpha \mathrm {CA} +2r\alpha \beta \mathrm {AB} =1.\end{aligned}}$

158. Conséquences de l’hypothèse des forces centrales. — Pour Cauchy toutes les forces sont centrales ; aussi, dans sa théorie de la double réfraction admet-il implicitement qu’il en est ainsi. Nous avons fait remarquer (17) que dans l’hypothèse des forces centrales, le nombre des coefficients numériques de la fonction $\mathrm {W} _{2}$ se trouvait réduit ; nous devons donc nous attendre à avoir dans ce cas un certain nombre de relations entre les douze coefficients numériques de l’ellipsoïde de polarisation. Cherchons ces relations.

Dans le premier chapitre de cet ouvrage, nous avons vu que si les forces sont centrales, on a

$\mathrm {W} _{2}=\sum {\frac {d\mathrm {F} }{d\mathrm {R} }}\rho _{2}+{\frac {1}{2}}\sum {\frac {d^{2}\mathrm {F} }{d\mathrm {R} ^{2}}}\rho _{1}^{2},$

où,

${\begin{aligned}\rho _{1}&=2(\mathrm {D} x\,\mathrm {D} \xi +\mathrm {D} y\,\mathrm {D} \eta +\mathrm {D} z\,\mathrm {D} \zeta ),\\[1.25ex]\rho _{2}&=\mathrm {D} \xi ^{2}+\mathrm {D} x^{2}+\mathrm {D} \zeta ^{2},\end{aligned}}$

et

${\begin{aligned}\mathrm {D} \xi &={\frac {d\xi }{dx}}\,\mathrm {D} x+{\frac {d\xi }{dy}}\,\mathrm {D} y+{\frac {d\xi }{dz}}\,\mathrm {D} z,\\[1.5ex]\mathrm {D} \eta &={\frac {d\eta }{dx}}\,\mathrm {D} x+{\frac {d\eta }{dy}}\,\mathrm {D} y+{\frac {d\eta }{dz}}\,\mathrm {D} z,\\[1.5ex]\mathrm {D} \zeta &={\frac {d\zeta }{dx}}\,\mathrm {D} x+{\frac {d\zeta }{dy}}\,\mathrm {D} y+{\frac {d\zeta }{dz}}\,\mathrm {D} z.\end{aligned}}$

Dans le cas d’une onde plane $\xi ,\,\eta ,\,\zeta$ étant de la forme

$\xi =\mathrm {A} e^{\mathrm {P} },\qquad \quad \eta =\mathrm {B} e^{\mathrm {P} },\qquad \quad \zeta =\mathrm {C} e^{\mathrm {P} },$

nous aurons

${\begin{aligned}\mathrm {D} \xi &={\frac {2i\pi }{\lambda }}\mathrm {A} e^{\mathrm {P} }(\alpha \,\mathrm {D} x+\beta \,\mathrm {D} y+\gamma \,\mathrm {D} z),\\[1.5ex]\mathrm {D} \eta &={\frac {2i\pi }{\lambda }}\mathrm {B} e^{\mathrm {P} }(\alpha \,\mathrm {D} x+\beta \,\mathrm {D} y+\gamma \,\mathrm {D} z),\\[1.5ex]\mathrm {D} \zeta &={\frac {2i\pi }{\lambda }}\mathrm {C} e^{\mathrm {P} }(\alpha \,\mathrm {D} x+\beta \,\mathrm {D} y+\gamma \,\mathrm {D} z)\,;\end{aligned}}$

et par conséquent,

${\begin{aligned}\rho _{1}=2\sum \mathrm {D} x\,\mathrm {D} \xi &={\frac {4i\pi }{\lambda }}e^{\mathrm {P} }\sum \mathrm {A} \,\mathrm {D} x\sum \alpha \,\mathrm {D} x,\\[1.5ex]\rho _{2}=\sum \mathrm {D} \xi ^{2}&=\left({\frac {2i\pi }{\lambda }}\right)^{2}e^{2\mathrm {P} }(\mathrm {A} ^{2}+\mathrm {B} ^{2}+\mathrm {C} ^{2})\left(\sum \alpha \,\mathrm {D} x\right)^{2},\\[1.5ex]\rho _{1}^{2}&=4\left({\frac {2i\pi }{\lambda }}\right)^{2}e^{2\mathrm {P} }\left[\sum \mathrm {A} \,\mathrm {D} x\sum \alpha \,\mathrm {D} x\right]^{2}.\\\end{aligned}}$

Il est facile de constater que dans $\rho _{2}$

${\begin{aligned}\mathrm {coef.~de} \;\alpha ^{2}\mathrm {B} ^{2}-\mathrm {coef.~de} \;4\alpha \beta \mathrm {AB} &=\left({\frac {2i\pi }{\lambda }}\right)^{2}e^{2\mathrm {P} }\,\mathrm {D} x^{2},\\[1.5ex]\mathrm {coef.~de} \;\alpha ^{2}\mathrm {C} ^{2}-\mathrm {coef.~de} \;4\alpha \gamma \mathrm {AC} &=\left({\frac {2i\pi }{\lambda }}\right)^{2}e^{2\mathrm {P} }\,\mathrm {D} x^{2},\\\end{aligned}}$

et que dans $\rho _{1}^{2}$,

${\begin{aligned}\mathrm {coef.~de} \;\alpha ^{2}\mathrm {B} ^{2}-\mathrm {coef.~de} \;4\alpha \beta \mathrm {AB} &=4\left({\frac {2i\pi }{\lambda }}\right)^{2}e^{2\mathrm {P} }(\mathrm {D} x^{2}\,\mathrm {D} y^{2}-\mathrm {D} x\,\mathrm {D} y\,\mathrm {D} x\,\mathrm {D} y)\\[1.5ex]\mathrm {coef.~de} \;\alpha ^{2}\mathrm {C} ^{2}-\mathrm {coef.~de} \;4\alpha \gamma \mathrm {AC} &=4\left({\frac {2i\pi }{\lambda }}\right)^{2}e^{2\mathrm {P} }(\mathrm {D} x^{2}\,\mathrm {D} z^{2}-\mathrm {D} x\,\mathrm {D} z\,\mathrm {D} x\,\mathrm {D} z)\\\end{aligned}}$

Dans $\rho _{1}^{2}$ et $\rho _{2},$ la relation

$\mathrm {coef.~de} \;\alpha ^{2}\mathrm {B} ^{2}-\mathrm {coef.~de} \;4\alpha \beta \mathrm {AB} =\mathrm {coef.~de} \;\alpha ^{2}\mathrm {C} ^{2}-\mathrm {coef.~de} \;4\alpha \gamma \mathrm {AC}$

est donc satisfaite ; par suite elle l’est dans $\mathrm {W} _{2}$ et aussi dans $\mathrm {H} .$ Par permutations circulaires, nous pouvons en déduire deux autres. Les douze coefficients numériques du premier membre de l’équation de l’ellipsoïde de polarisation étant liés par trois relations, neuf seulement de ces coefficients sont arbitraires. Les trois relations entre les coefficients de l’équation (1) sont :

(2)

${\begin{aligned}\lambda '-{\frac {r}{2}}&=\lambda ''-{\frac {q}{2}}\\[1.5ex]\mu ''-{\frac {p}{2}}&=\mu \,-{\frac {r}{2}}\\[1.5ex]\nu -{\frac {q}{2}}&=\nu '-{\frac {p}{2}}\\\end{aligned}}$

159. Vibrations quasi-transversales et vibrations quasi-longitudinales. — Les vibrations d’une onde plane se propageant dans un milieu anisotrope devant être dirigées suivant les axes de l’ellipsoïde de polarisation (147) il faut, pour qu’elles soient rigoureusement transversales ou longitudinales par rapport au plan de l’onde, que ce plan soit un des plans principaux de l’ellipsoïde de polarisation. Cette condition sera réalisée si la normale au plan de l’onde est un des axes de l’ellipsoïde, c’est-à-dire si $\alpha ,\,\beta ,\,\gamma$ satisfont aux équations

$\mathrm {AS} ={\frac {1}{2}}{\frac {d\Pi }{d\mathrm {A} }},\qquad \mathrm {BS} ={\frac {1}{2}}{\frac {d\Pi }{d\mathrm {B} }},\qquad \mathrm {CS} ={\frac {1}{2}}{\frac {d\Pi }{d\mathrm {C} }}\cdot$

Tirant de l’équation (1) de l’ellipsoïde de polarisation de Cauchy les valeurs des seconds membres de ces dernières équations et remplaçant ensuite $\mathrm {A}$ par $\alpha ,$ $\mathrm {B}$ par $\beta$ et $\mathrm {C}$ par $\gamma ,$ nous obtenons après réduction

${\begin{aligned}S&=\lambda \alpha ^{2}+\mu \beta ^{2}+\nu \gamma ^{2}+q\gamma ^{2}+r\beta ^{2},\\[1.5ex]S&=\lambda '\alpha ^{2}+\mu '\beta ^{2}+\nu '\gamma ^{2}+r\alpha ^{2}+p\gamma ^{2},\\[1.5ex]S&=\lambda ''\alpha ^{2}+\mu ''\beta ^{2}+\nu ''\gamma ^{2}+p\beta ^{2}+q\alpha ^{2}\cdot \\\end{aligned}}$

Pour que ces équations soient satisfaites quels que soient $\alpha ,\,\beta ,\,\gamma ,$ il faut que les coefficients de $\alpha ^{2},$ $\beta ^{2},$ $\gamma ^{2}$ soient les mêmes dans les trois équations : on a donc

${\begin{aligned}\lambda =\lambda '+r&=\lambda ''+q,\\[1.5ex]\mu +r=\mu '&=\mu ''+p,\\[1.5ex]\nu +q=\nu '&+p=\nu ''.\\\end{aligned}}$

Or ces relations jointes aux relations (2) déduites de l’hypothèse des forces centrales exigent que l’on ait

$p=q=r,$

et elles deviennent alors,

${\begin{alignedat}{6}\lambda &=\lambda '+p,\qquad \quad &\lambda '&=\lambda '';\\[1.5ex]\mu &=\mu '-p,\qquad \quad &\mu '&=\mu ''+p,\\[1.5ex]\nu &=\nu ',\qquad \quad &\nu '&=\nu ''-p.\\\end{alignedat}}$

Ces dernières relations ci induisent aux égalités

${\begin{aligned}\lambda \alpha ^{2}+\mu \beta ^{2}+\nu \gamma ^{2}-p\alpha ^{2}&=\lambda '\,\alpha ^{2}+\mu '\,\beta ^{2}+\nu '\,\gamma ^{2}-p\beta ^{2}\\&=\lambda ''\alpha ^{2}+\mu ''\beta ^{2}+\nu ''\gamma ^{2}-p\gamma ^{2}\\\end{aligned}}$

Il est facile de s’assurer que ce sont là les conditions auxquelles conduisent l’application à l’équation (1) des formules connues qui expriment qu’un ellipsoïde est de révolution autour d’un axe ayant pour cosinus directeurs $\alpha ,\,\beta ,\,\gamma .$ Par conséquent, les vibrations ne peuvent être rigoureusement transversales ou longitudinales que si l’ellipsoïde de polarisation est de révolution autour de la normale au plan de l’onde. Une telle conséquence est inadmissible, car les deux ondes planes à vibrations rectangulaires et transversales qui résultent de l’onde plane incidente auraient même vitesse de propagation et la double réfraction ne s’expliquerait pas.

Ainsi les hypothèses de Cauchy conduisent à admettre qu’une onde plane donne naissance, en se propageant dans un milieu anisotrope, à trois ondes planes dont les directions de vibration ne sont ni normales au plan de l’onde, ni situées dans ce plan. Mais la biréfringence étant très faible dans toutes les substances jouissant de la double réfraction, les vibrations de deux des ondes planes seront quasi-transversales et celles de la troisième, quasi-longitudinales.

L’existence de vibrations quasi-transversales n’est pas absolument contraire à nos connaissances sur la direction des vibrations lumineuses, car si l’expérience nous apprend que dans l’air les vibrations doivent être rigoureusement transversales, rien ne nous prouve qu’il en est ainsi à l’intérieur d’un cristal. Quant au rayon dont les vibrations sont quasi-longitudinales, Cauchy ne put tout d’abord expliquer pourquoi il n’avait d’existence réelle ; il est probable que s’il avait eu occasion de revenir sur la double réfraction, il eût admis que ce rayon était évanescent.

160. Vitesses de propagation des ondes. — La théorie de Fresnel se trouvant vérifiée par les expériences les plus délicates, toute théorie de la double réfraction doit conduire aux mêmes conséquences que celle de Fresnel ; en particulier on doit arriver aux mêmes valeurs pour les vitesses de propagation des ondes réelles. Ces vitesses étant, dans la théorie de Cauchy, inversement proportionnelles aux axes de l’ellipsoïde de polarisation et, dans celle de Fresnel, aux axes de l’ellipse $\mathrm {E}$ d’intersection du plan de l’onde avec l’ellipsoïde d’élasticité, il faut, pour qu’elles aient une même valeur, que l’ellipse $\mathrm {E}$ se confonde avec l’une des sections principales de l’ellipsoïde de polarisation. Or s’il en était ainsi, le plan de l’onde, qui contient l’ellipse $\mathrm {E} ,$ serait un plan principal de l’ellipsoïde de polarisation de Cauchy, ce qui ne peut avoir lieu, comme nous venons de le démontrer. Par conséquent, les vitesses théoriques de propagation des ondes ne peuvent avoir les mêmes valeurs dans les deux théories. Mais en assujettissant, comme le fait Cauchy, l’ellipsoïde de polarisation à passer par l’ellipse $\mathrm {E} ,$ les différences entre ces valeurs deviennent de l’ordre des erreurs expérimentales.

En effet, soit

$ax^{2}+by^{2}+cz^{2}=1$

l’équation de l’ellipsoïde de polarisation de Cauchy rapporté à ses axes. À cause de la faible biréfringence des cristaux, le plan de l’onde fait un angle infiniment petit avec l’un des plans principaux de cet ellipsoïde, par exemple, avec le plan $z=0.$ En appelant $\alpha ,\,\beta ,\,\gamma$ les cosinus directeurs de la normale au plan de l’onde, $\alpha$ et $\beta$ seront des infiniment petits. D’après nos conventions, l’intersection de l’ellipsoïde par le plan de l’onde est l’ellipse $\mathrm {E} .$ Les inverses des carrés des axes de cette section sont donnés par les racines de l’équation en $\mathrm {R} ,$

$\alpha ^{2}(b-\mathrm {R} )(c-\mathrm {R} )+\beta ^{2}(c-\mathrm {R} )(a-\mathrm {R} )+\gamma ^{2}(a-\mathrm {R} )(b-\mathrm {R} )=0\,;$

en négligeant les carrés de $\alpha$ et de $\beta$ cette équation se réduit à la suivante

$(a-\mathrm {R} )(b-\mathrm {R} )=0,$

dont les racines $a$ et $b$ sont précisément les inverses des carrés des deux axes principaux de l’ellipsoïde de polarisation situés dans le plan $z=0.$ Par conséquent, ces axes ne diffèrent de ceux de l’ellipse $\mathrm {E}$ que par des infiniment petits du second ordre ; il en sera de même de leurs inverses et par suite des valeurs des vitesses de propagation.

161. Équation de l’ellipsoïde de polarisation de Cauchy. — En résumé, Cauchy admet l’existence de trois plans de symétrie optique, suppose les forces centrales et assujettit son ellipsoïde de polarisation à passer par l’ellipse d’intersection du plan de l’onde et de l’ellipsoïde d’élasticité de Fresnel. Cette dernière hypothèse permet de trouver facilement l’équation de l’ellipsoïde de polarisation.

L’équation de l’ellipsoïde d’élasticité étant

$a\mathrm {A} ^{2}+b\mathrm {B} ^{2}+c\mathrm {C} ^{2}=1,$

celle du plan de l’onde

$\alpha \mathrm {A} +\beta \mathrm {B} +\gamma \mathrm {C} =0,$

l’équation de l’ellipsoïde passant par l’intersection de ces deux surfaces est de la forme

$\Pi =(a\mathrm {A} ^{2}+b\mathrm {B} ^{2}+c\mathrm {C} ^{2})+(\alpha \mathrm {A} +\beta \mathrm {B} +\gamma \mathrm {C} )(\alpha _{1}\mathrm {A} +\beta _{1}\mathrm {B} +\gamma _{1}\mathrm {C} )=1.$

Cette équation sera homogène et du second degré par rapport à $\alpha ,\,\beta ,\,\gamma$ et par rapport à $\mathrm {A,\,B,\,C} ,$ en l’écrivant

${\begin{aligned}\Pi &=(a\mathrm {A} ^{2}+b\mathrm {B} ^{2}+c\mathrm {C} ^{2})(\alpha ^{2}+\beta ^{2}+\gamma ^{2})\\&+(\alpha \mathrm {A} +\beta \mathrm {B} +\gamma \mathrm {C} )(\alpha _{1}\mathrm {A} +\beta _{1}\mathrm {B} +\gamma _{1}\mathrm {C} )=1,\\\end{aligned}}$

et en admettant que $\alpha _{1},\,\beta _{1},\,\gamma _{1}$ sont des fonctions linéaires et plans de symétrie optique, l’équation précédente ne doit pas changer, quand on change simultanément les signes de $\alpha$ et de $\mathrm {A} ,$ ou de $\beta$ et $\mathrm {B} ,$ ou enfin de $\gamma$ et $\mathrm {C} .$ Les fonctions linéaires $\alpha _{1},\,\beta _{1},\,\gamma _{1}$ doivent donc se réduire à

$\alpha _{1}=a_{1}\alpha ,\qquad \beta _{1}=b_{1}\beta ,\qquad \gamma _{1}=c_{1}\gamma \,;$

en portant ces valeurs dans l’équation de l’ellipsoïde de polarisation, elle devient

(1)

${\begin{aligned}\Pi &=(\alpha ^{2}+\beta ^{2}+\gamma ^{2})(a\mathrm {A} ^{2}+b\mathrm {B} ^{2}+c\mathrm {C} ^{2})\\&+(\alpha \mathrm {A} +\beta \mathrm {B} +\gamma \mathrm {C} )(a_{1}\alpha \mathrm {A} +b_{1}\beta \mathrm {B} +c_{1}\gamma \mathrm {C} )=1.\end{aligned}}$

Si nous admettons maintenant que les forces sont centrales nous aurons entre les coefficients de cette équation, trois relations dont la première est

$\mathrm {coef.~de} \;\alpha ^{2}\mathrm {B} ^{2}-\mathrm {coef.~de} \;4\alpha \beta \mathrm {AB} =\mathrm {coef.~de} \;\alpha ^{2}\mathrm {C} ^{2}-\mathrm {coef.~de} \;4\alpha \gamma \mathrm {AC} \,;$

elle donne :

$b-4(a_{1}+b_{1})=c-4(a_{1}+c_{1}).$

Les deux autres conduisent à

${\begin{aligned}c-4(b_{1}+c_{1})=a-4(b_{1}+a_{1}),\\[1.25ex]a-4(c_{1}+a_{1})=b-4(c_{1}+b_{1}).\\\end{aligned}}$

Ces trois dernières relations peuvent d’ailleurs s’écrire

$a-4a_{1}=b-4b_{1}=c-4c_{1}\cdot$

Telles sont les conditions introduites par l’hypothèse des forces centrales ; il serait facile de montrer que, quand elles sont remplies, le plan de l’onde n’est pas un plan de symétrie de l’ellipsoïde.

162. Si nous abandonnons l’hypothèse des forces centrales, le plan de l’onde pourra devenir un plan de symétrie de l’ellipsoïde de polarisation. Il faut pour cela que la perpendiculaire au plan de l’onde soit un axe principal, c’est-à-dire que $\alpha ,\,\beta ,\,\gamma ,$ satisfassent aux équations des directions principales de l’ellipsoïde (1) du paragraphe précédent. La première de ces équations est

${\begin{aligned}\mathrm {AS} ={\frac {1}{2}}{\frac {d\Pi }{d\mathrm {A} }}=a\mathrm {A} (\alpha ^{2}+\beta ^{2}+\gamma ^{2})+{\frac {1}{2}}&\alpha (a_{1}\alpha \mathrm {A} +b_{1}\beta \mathrm {B} +c_{1}\gamma \mathrm {C} )\\&+{\frac {1}{2}}a_{1}\alpha (\alpha \mathrm {A} +\beta \mathrm {B} +\gamma \mathrm {C} )\,;\\\end{aligned}}$

en y remplaçant $\mathrm {A,\,B,\,C}$ par $\alpha ,\,\beta ,\,\gamma$ elle donne, après simplification,

$\mathrm {S} =\left(a+{\frac {a_{1}}{2}}\right)(\alpha ^{2}+\beta ^{2}+\gamma ^{2})+{\frac {1}{2}}(a_{1}\alpha ^{2}+b_{1}\beta ^{2}+c_{1}\gamma ^{2}).$

Les deux autres équations conduiraient à

${\begin{aligned}\mathrm {S} &=\left(b+{\frac {b_{1}}{2}}\right)(\alpha ^{2}+\beta ^{2}+\gamma ^{2})+{\frac {1}{2}}(a_{1}\alpha ^{2}+b_{1}\beta ^{2}+c_{1}\gamma ^{2}),\\[1.5ex]\mathrm {S} &=\left(c+{\frac {c_{1}}{2}}\right)\,(\alpha ^{2}+\beta ^{2}+\gamma ^{2})+{\frac {1}{2}}(a_{1}\alpha ^{2}+b_{1}\beta ^{2}+c_{1}\gamma ^{2}).\\\end{aligned}}$

Pour que ces trois dernières équations se réduisent à une, il faut et il suffit que l’on ait

$a+{\frac {a_{1}}{2}}=b+{\frac {b_{1}}{2}}=c+{\frac {c_{1}}{2}}\cdot$

En particulier, si on a

(2)

$a+{\frac {a_{1}}{2}}=b+{\frac {b_{1}}{2}}=c+{\frac {c_{1}}{2}}=0,$

le plan de l’onde sera un plan principal de l’ellipsoïde de polarisation et les vibrations seront rigoureusement transversales et longitudinales. Les vitesses de propagation des ondes dont les vibrations sont transversales sont inversement proportionnelles aux axes de l’ellipse d’intersection ; celle de l’onde dont les vibrations sont longitudinales est proportionnelle à l’inverse de l’axe normal à l’onde, c’est-à-dire à la racine carrée de

$\mathrm {S} =\left(c+{\frac {c_{1}}{2}}\right)(\alpha ^{2}+\beta ^{2}+\gamma ^{2})+{\frac {1}{2}}(a_{1}\alpha ^{2}+b_{1}\beta ^{2}+c_{1}\gamma ^{2})\,;$

quantité qui, par suite des relations (2), se réduit à

$\mathrm {S} ={\frac {1}{2}}(a_{1}\alpha ^{2}+b_{1}\beta ^{2}+c_{1}\gamma ^{2}).$

Or, puisque $a,\,b,\,c$ sont positifs, il résulte des relations (2) que $a_{1},\,b_{1},\,c_{1}$ sont négatifs ; $\mathrm {S}$ sera négatif, la vitesse de propagation des vibrations longitudinales est imaginaire, et le rayon longitudinal évanescent.

On retrouve donc ainsi très facilement toutes les conséquences de la théorie de Fresnel.

THÉORIE DE NEUMANN

163. Hypothèses de Neumann. — Les hypothèses particulières à cette théorie trouvée presque simultanément par Lamé, Neumann et Mac-Cullagh sont les suivantes :

1^o Le plan de l’onde est un plan de symétrie de l’ellipsoïde de polarisation.

2^o La vitesse de propagation du rayon longitudinal est nulle.

Il résulte de ces hypothèses que l’ellipsoïde de polarisation se réduit à un cylindre dont les génératrices sont perpendiculaires au plan de l’onde. Si nous désignons par $\mathrm {A',\,B',\,C'}$ les quantités proportionnelles aux cosinus directeurs de la vibration que nous désignions par $\mathrm {A,\,B,\,C}$ dans les théories précédentes, et si nous continuons à appeler $\alpha ,\,\beta ,\,\gamma$ les cosinus directeurs de la normale au plan de l’onde, le premier membre $\Pi$ de l’équation de l’ellipsoïde de polarisation sera une fonction homogène du second degré par rapport à $\mathrm {A',\,B',\,C'}$ et par rapport à $\alpha ,\,\beta ,\,\gamma .$ Cet ellipsoïde se réduira à un cylindre à génératrices normales au plan de l’onde si les équations

(1)

${\frac {d\Pi }{d\mathrm {A'} }}=0,\qquad {\frac {d\Pi }{d\mathrm {B'} }}=0,\qquad {\frac {d\Pi }{d\mathrm {C'} }}=0,$

qui expriment que l’un des axes de l’ellipsoïde est nul, sont satisfaites pour $\mathrm {A} '=\alpha ,$ $\mathrm {B} '=\beta ,$ $\mathrm {C} '=\gamma .$

164. Équation du cylindre de polarisation. — Si nous posons

(2)

${\begin{aligned}\mathrm {A} &=\mathrm {C} '\beta -\mathrm {B} '\gamma ,\\[1.5ex]\mathrm {B} &=\mathrm {A} '\gamma -\mathrm {C} '\alpha ,\\[1.5ex]\mathrm {B} &=\mathrm {B} '\alpha -\mathrm {A} '\beta ,\\\end{aligned}}$

le premier membre de l’équation

(3)

$\Pi =a\mathrm {A} ^{2}+b\mathrm {B} ^{2}+c\mathrm {C} ^{2}+2d\mathrm {BC} +2e\mathrm {CA} +2f\mathrm {AB} =1,$

sera homogène, et du second degré par rapport à $\mathrm {A',\,B',\,C'}$ et par rapport à $\alpha ,\,\beta ,\,\gamma \,;$ nous allons démontrer que c’est l’équation du cylindre de polarisation de Neumann.

Nous allons d’abord faire voir que si le polynôme $\Pi$ est de cette forme, les équations (1) sont satisfaites quand on y remplace $\mathrm {A',\,B',\,C'}$ par $\alpha ,\,\beta ,\,\gamma .$ On a en effet

${\begin{aligned}{\frac {1}{2}}{\frac {d\Pi }{d\mathrm {A} '}}=(a\mathrm {A} +e\mathrm {C} +f\mathrm {B} ){\frac {d\mathrm {A} }{d\mathrm {A} '}}+(b\mathrm {B} &+d\mathrm {C} +f\mathrm {A} ){\frac {d\mathrm {B} }{d\mathrm {A} '}}\\&+(c\mathrm {C} +d\mathrm {B} +e\mathrm {A} ){\frac {d\mathrm {C} }{d\mathrm {A} '}}\cdot \\\end{aligned}}$

Or, si dans les relations (2) on fait $\mathrm {A} '=\alpha ,$ $\mathrm {B} '=\beta ,$ $\mathrm {C} '=\gamma ,$ on trouve $\mathrm {A} =\mathrm {B} =\mathrm {C} =0\,;$ par conséquent, quand on fera cette substitution dans l’équation précédente, les coefficients des dérivées qui entrent dans le second membre seront nuls et on aura ${\frac {d\Pi }{d\mathrm {A} '}}=0.$ On démontrerait d’une manière analogue que les deux dernières des équations (1) sont également satisfaites. L’équation (3) représente donc bien un cylindre dont les génératrices sont parallèles à la direction $\alpha ,\,\beta ,\,\gamma .$

Pour compléter la démonstration il faut démontrer que réciproquement, si $\Pi =1$ est l’équation d’un cylindre dont les génératrices sont normales au plan de l’onde, cette équation peut se mettre sous la forme (3), $\mathrm {A,\,B,\,C}$ étant définis par les relations (2). Nous laisserons au lecteur le soin de démontrer cette réciproque.

Nous pouvons prendre les axes de coordonnées de manière à faire disparaître les termes rectangles de l’équation (3) qui alors se réduit à

(4)

$\Pi =a\mathrm {A} ^{2}+b\mathrm {B} ^{2}+c\mathrm {C} ^{2}=1.$

Les nouveaux axes de coordonnées sont alors les plans de symétrie optique du milieu. En effet, si l’on se reporte aux équations (2), on voit que le changement de $\mathrm {A} '$ en $-\mathrm {A} '$ et de $\alpha$ en $-\alpha$ ne change pas la valeur de $\mathrm {A}$ et ne fait que changer les signes de $\mathrm {B}$ et de $\mathrm {C} \,;$ ces quantités n’entrant dans $\Pi$ que par leurs carrés, ce polynôme conservera la même valeur quand on changera les signes de A' et de $\alpha ,$ et par suite, le plan des $yz$ est un plan de symétrie optique. Un raisonnement analogue montrerait que les deux autres plans de coordonnées sont également des plans de symétrie optique. Ce sont donc les mêmes que ceux que nous avons pris dans la théorie de Fresnel et celle de Cauchy.

165. Propagation d’une onde plane. — Les équations de condition qui donnent les directions de vibration et les vitesses de propagation d’une onde plane sont ici

$\mathrm {A'V} ^{2}={\frac {1}{2}}{\frac {d\Pi }{d\mathrm {A} '}}={\frac {1}{2}}\left({\frac {d\Pi }{d\mathrm {A} }}{\frac {d\mathrm {A} }{d\mathrm {A} '}}+{\frac {d\Pi }{d\mathrm {B} }}{\frac {d\mathrm {B} }{d\mathrm {A} '}}+{\frac {d\Pi }{d\mathrm {C} }}{\frac {d\mathrm {C} }{d\mathrm {A} '}}\right),$

ou

$\mathrm {A'V^{2}} =b\gamma \mathrm {B} -c\beta \mathrm {C} ,$

et

${\begin{aligned}\mathrm {B'V^{2}} &=c\alpha \mathrm {C} -a\gamma \mathrm {A} ,\\[1.5ex]\mathrm {C'V^{2}} &=a\beta \mathrm {A} -b\alpha \mathrm {B} .\end{aligned}}$

Ces trois équations peuvent être remplacées par un système de trois autres ne contenant plus $\mathrm {A',\,B',\,C'} .$ Pour cela multiplions la troisième par $\beta ,$ la seconde par $\gamma$ et retranchons ce dernier produit du premier ; nous obtiendrons

$(\mathrm {C} '\beta -\mathrm {B} '\gamma )\mathrm {V} ^{2}=a\mathrm {A} (\beta ^{2}+\gamma ^{2})-\alpha (b\beta \mathrm {B} -c\gamma \mathrm {C} ),$

et en remplaçant $\mathrm {C} '\beta -\mathrm {B} '\gamma$ par $\mathrm {A} ,$ puis ajoutant l’identité

$0=a\mathrm {A} \alpha ^{2}-\alpha (a\alpha \mathrm {A} ),$

nous aurons

$\mathrm {AV} ^{2}=a\mathrm {A} (\alpha ^{2}+\beta ^{2}+\gamma ^{2})-\alpha (a\alpha \mathrm {A} +b\beta \mathrm {B} +c\gamma \mathrm {C} ).$

Si nous posons

$\mathrm {H} =a\alpha \mathrm {A} +b\beta \mathrm {B} +c\gamma \mathrm {C} ,$

l’équation précédente et les deux qui s’en déduisent par permutation deviennent

${\begin{aligned}\mathrm {AV} ^{2}&=a\mathrm {A} -\alpha \mathrm {H} ,\\[1.25ex]\mathrm {BV} ^{2}&=b\mathrm {B} -\beta \mathrm {H} ,\\[1.25ex]\mathrm {CV} ^{2}&=c\mathrm {C} -\gamma \mathrm {H} .\\\end{aligned}}$

Ce sont les équations que nous avons déjà trouvées (154) en exposant la théorie de Fresnel ; elles nous montrent donc que les quantités $\mathrm {A,\,B,\,C}$ sont proportionnelles aux cosinus directeurs de la vibration de Fresnel, et qu’en outre les vitesses de propagation ont les mêmes valeurs dans les deux théories.

Dans ces deux théories les vibrations ont lieu dans le plan de l’onde ; il est facile de voir qu’elles sont rectangulaires. En effet si nous multiplions les relations (2) successivement par $\mathrm {A'} ,$ $\mathrm {B'} ,$ $\mathrm {C'} ,$ et si nous additionnons, nous obtenons

$\mathrm {AA} '\!+\!\mathrm {BB} '\!+\!\mathrm {CC} '\!=\!\mathrm {A'C'} \beta \!-\!\mathrm {A'B'} \gamma \!+\!\mathrm {A'B'} \gamma \!-\!\mathrm {B'C'} \alpha \!+\!\mathrm {B'C'} \alpha \!-\!\mathrm {A'C'} \beta \!=\!0.$

La théorie de Neumann ne diffère donc de celle de Fresnel qu’en ce que la vibration au lieu d’être normale au plan de polarisation est parallèle à ce plan ; par suite toutes deux rendront également bien compte des faits expérimentaux puisque l’expérience ne peut indiquer si la vibration est parallèle ou normale au plan de polarisation.

166. Équations de Lamé. — Les équations du mouvement d’une molécule d’une onde plane dans un milieu élastique satisfaisant aux hypothèses de Neumann peuvent être mises sous une forme intéressante en introduisant les quantités $u,\,v,\,w$ définies par les relations

${\begin{aligned}u&={\frac {d\zeta }{dy}}-{\frac {d\eta }{dz}},\\[1.25ex]v&={\frac {d\xi }{dz}}-{\frac {d\zeta }{dx}},\\[1.25ex]w&={\frac {d\eta }{dx}}-{\frac {d\xi }{dy}}\cdot \end{aligned}}$

Ces quantités, quand on y remplace $\xi ,\,\eta ,\,\zeta$ par les valeurs

$\xi =\mathrm {A} 'e^{\mathrm {P} },\qquad \eta =\mathrm {B} 'e^{\mathrm {P} },\qquad \zeta =\mathrm {C} 'e^{\mathrm {P} },\qquad$

deviennent

(5)

${\begin{aligned}u&={\frac {2i\pi }{\lambda }}e^{\mathrm {P} }(\mathrm {C} '\beta -\mathrm {B} '\gamma )={\frac {2i\pi }{\lambda }}\mathrm {A} e^{\mathrm {P} },\\[1.5ex]v&={\frac {2i\pi }{\lambda }}e^{\mathrm {P} }(\mathrm {A} '\gamma -\mathrm {C} '\alpha )={\frac {2i\pi }{\lambda }}\mathrm {B} e^{\mathrm {P} },\\[1.5ex]w&={\frac {2i\pi }{\lambda }}e^{\mathrm {P} }(\mathrm {B} '\alpha -\mathrm {A} '\beta )={\frac {2i\pi }{\lambda }}\mathrm {C} e^{\mathrm {P} }.\end{aligned}}$

D’autre part, on a

(6)

${\begin{aligned}{\frac {d^{2}\xi }{dt^{2}}}&=\left(\mathrm {\frac {2i\pi }{\lambda }} \right)^{2}e^{\mathrm {P} }\mathrm {A'V} ^{2},\\[1.5ex]{\frac {d^{2}\eta }{dt^{2}}}&=\left(\mathrm {\frac {2i\pi }{\lambda }} \right)^{2}e^{\mathrm {P} }\mathrm {B'V} ^{2},\\[1.5ex]{\frac {d^{2}\zeta }{dt^{2}}}&=\left(\mathrm {\frac {2i\pi }{\lambda }} \right)^{2}e^{\mathrm {P} }\mathrm {C'V} ^{2}.\end{aligned}}$

Or, la première des équations de condition trouvées dans le paragraphe précédent donne, quand on multiplie ses deux membres par $\left({\frac {2i\pi }{\lambda }}\right)^{2}e^{\mathrm {P} },$

$\left({\frac {2i\pi }{\lambda }}\right)^{2}e^{\mathrm {P} }\mathrm {A'V} ^{2}=\left({\frac {2i\pi }{\lambda }}\right)^{2}b\gamma \mathrm {B} e^{\mathrm {P} }-\left({\frac {2i\pi }{\lambda }}\right)^{2}c\beta \mathrm {C} e^{\mathrm {P} },$

et il est facile de voir, en calculant les dérivées partielles de $u,\,v,\,w$ par rapport à $x,\,y,\,z,$que cette équation peut s’écrire

$\left({\frac {2i\pi }{\lambda }}\right)^{2}e^{\mathrm {P} }\mathrm {A'V} ^{2}=b\,{\frac {dv}{dz}}-c\,{\frac {dw}{dy}}\cdot$

Il résulte de ces transformations et des transformations analogues que l’on pourrait effectuer sur les seconds membres des équations (6) que ces équations se réduisent à

(7)

${\begin{aligned}{\frac {d^{2}\xi }{dt^{2}}}&=b\,{\frac {dv}{dz}}-c\,{\frac {dw}{dy}}\\[1.5ex]{\frac {d^{2}\eta }{dt^{2}}}&=c\,{\frac {dw}{dx}}-a\,{\frac {du}{dz}}\\[1.5ex]{\frac {d^{2}\zeta }{dt^{2}}}&=a\,{\frac {du}{dy}}-b\,{\frac {dv}{dx}}\end{aligned}}$

Ces équations seront satisfaites pour les déplacements $\xi ,\,\eta ,\,\zeta$ des molécules d’une onde plane vibrant suivant les hypothèses de Neumann. C’est sous cette forme que les équations du mouvement de ces molécules ont été trouvées par Lamé.

Remarquons que, d’après les équations (5), $u,\,v,\,w$ sont les composantes du déplacement d’une molécule d’une onde plane dans la théorie de Fresnel quand $\xi ,\,\eta ,\,\zeta$ satisfaisant aux équations (7), sont les valeurs des composantes du déplacement dans la théorie de Neumann. De là résulte une méthode commode pour trouver les équations du mouvement d’une molécule dans la théorie de Fresnel. En effet, si de la dérivée par rapport à $y$ de la troisième des équations (7) nous retranchons la dérivée par rapport à $z$ de la seconde, nous obtenons

${\frac {d}{dy}}{\frac {d^{2}\zeta }{dt^{2}}}-{\frac {d}{dz}}{\frac {d^{2}\eta }{dt^{2}}}=a\,{\frac {d^{2}u}{dy^{2}}}-b\,{\frac {d^{2}v}{dx\,xy}}-c\,{\frac {d^{2}w}{dx\,dz}}+a\,{\frac {d^{2}u}{dz^{2}}}$,

ou

${\frac {d^{2}}{dt^{2}}}\left({\frac {d\zeta }{dy}}-{\frac {d\eta }{dz}}\right)=a\left({\frac {d^{2}u}{dx^{2}}}+{\frac {d^{2}u}{dy^{2}}}+{\frac {d^{2}u}{dz^{2}}}\right)-a\,{\frac {d^{2}u}{dx^{2}}}-b\,{\frac {d^{2}v}{dx\,xy}}-c\,{\frac {d^{2}w}{dx\,dz}}$

ou encore

${\frac {d^{2}u}{dt^{2}}}=a\Delta u-a\,{\frac {d^{2}u}{dx^{2}}}-b\,{\frac {d^{2}v}{dx\,xy}}-c\,{\frac {d^{2}w}{dx\,dz}}\cdot$

On trouverait par une marche analogue deux autres équations qui, avec la précédente, détermineraient les valeurs de $u,\,v,\,w$ pour une molécule d’une onde plane. La substitution de $u=\mathrm {A} e^{\mathrm {P} },$ $v=\mathrm {B} e^{\mathrm {P} },$ $w=\mathrm {C} e^{\mathrm {P} }$ dans ces équations doit évidemment conduire aux équations que nous avons déduites des hypothèses de Fresnel (154) et que nous avons retrouvées précédemment (165) ; c’est ce dont il est facile de s’assurer.

THÉORIE DE M. SARRAU

167. Équations du mouvement. — M. Sarrau prend pour bases de sa théorie les mêmes hypothèses que Briot dans sa théorie de la dispersion, hypothèses que nous avons déjà énoncées dans le chapitre précédent (140). Dans cette théorie les équations du mouvement sont

(1)

${\begin{aligned}\rho {\frac {d^{2}\xi }{dt^{2}}}&=\Delta \xi -{\frac {d\Theta }{dx}}\\[1.5ex]\rho {\frac {d^{2}\eta }{dt^{2}}}&=\Delta \eta -{\frac {d\Theta }{dy}}\\[1.5ex]\rho {\frac {d^{2}\zeta }{dt^{2}}}&=\Delta \zeta -{\frac {d\Theta }{dz}}\\\end{aligned}}$

où $\rho$ est une fonction périodique des coordonnées qui, développée en série trigonométrique, peut s’écrire :

$\rho =\sum \mathrm {R} \sin(ax+by+cz+d)\cdot$

La valeur moyenne de tous les termes de cette série étant nulle, sauf celle du terme où l’on a $a=b=c=0,$ la valeur moyenne de $\rho$ est égale à $\mathrm {R} \sin d.$ À cause de cette périodicité imposée à la densité la résolution des équations du mouvement nécessite des calculs pénibles et, malgré les simplifications introduites par M. Potier, ils sont encore longs.

168. Propagation d’une onde plane. — Si nous posons,

(2)

$\xi =\mathrm {L} e^{\mathrm {P} },\qquad \eta =\mathrm {M} e^{\mathrm {P} },\qquad \zeta =\mathrm {N} e^{\mathrm {P} },$

où

$\mathrm {P} =2{\frac {i\pi }{\lambda }}(\alpha x+\beta y+\gamma z-\mathrm {V} t),$

$\alpha ,\,\beta ,\,\gamma$ et $\lambda$ étant des constantes, ces quantités représenteront les composantes du déplacement d’une molécule d’une onde plane $\alpha x+\beta y+\gamma z=0.$

En choisissant une unité de longueur très petite, de l’ordre des distances qui séparent les molécules, $\lambda$ sera exprimé par un nombre très grand et par conséquent ${\frac {2\pi }{\lambda }}$, que nous désignerons par $\mu ,$ sera une quantité très petite. Nous pourrons donc dans les calculs négliger les termes contenant $\mu ^{n}$ en facteur, la valeur de l’exposant $n$ variant avec le but que l’on se propose. En conservant les termes du premier degré on trouve l’explication de la polarisation rotatoire et nous avons montré qu’en conservant ceux du second degré on explique le phénomène de la dispersion. Dans la théorie de la double réfraction on peut négliger toutes les puissances de $\mu .$ Cherchons ce que donnent dans cette hypothèse, les équations (1) quand on y remplace $\xi ,\,\eta$ et $\zeta$ par leurs valeurs (2) en admettant, puisque $\rho$ est une fonction périodique des coordonnées, que $\mathrm {L,\,M,\,N}$ sont également des fonctions périodiques.

Nous obtiendrons pour $\Theta ,$

$\Theta ={\frac {d\xi }{dx}}+{\frac {d\eta }{dy}}+{\frac {d\zeta }{dz}}=e^{\mathrm {P} }\left[{\frac {d\mathrm {L} }{dx}}+{\frac {d\mathrm {M} }{dy}}+{\frac {d\mathrm {N} }{dz}}+i\mu (\alpha \mathrm {L} +\beta \mathrm {M} +\gamma \mathrm {N} )\right]\,;$

et si, pour simplifier, nous posons :

(3)

${\frac {d\mathrm {L} }{dx}}+{\frac {d\mathrm {M} }{dy}}+{\frac {d\mathrm {N} }{dz}}=\mathrm {T} ,$

(4)

$\alpha \mathrm {L} \,+\,\beta \mathrm {M} \,+\,\gamma \mathrm {N} \,=\mathrm {Q} ,$

nous aurons

$\Theta =e^{\mathrm {P} }\left(\mathrm {T} +i\mu \mathrm {Q} \right).$

De cette dernière expression nous tirons,

${\frac {d\Theta }{dx}}=e^{\mathrm {P} }\left[{\frac {d\mathrm {T} }{dx}}+i\mu \left(\alpha \mathrm {T} +{\frac {d\mathrm {Q} }{dx}}\right)-\mu ^{2}\alpha \mathrm {Q} \right].$

Le calcul de la dérivée seconde ${\frac {d^{2}\xi }{dx^{2}}}$ donne

${\frac {d^{2}\xi }{dx^{2}}}=e^{\mathrm {P} }\left({\frac {d^{2}\mathrm {L} }{dx^{2}}}+2i\mu \alpha {\frac {d\mathrm {L} }{dx}}-\mu ^{2}\alpha ^{2}\mathrm {L} \right)\,;$

par conséquent nous aurons pour $\Delta \xi ,$

$\Delta \xi =e^{\mathrm {P} }\left(\Delta \mathrm {L} +2i\mu {\frac {d\mathrm {L} }{dn}}-\mu ^{2}\mathrm {L} \right),$

en posant

${\frac {d\mathrm {L} }{dn}}=\alpha {\frac {d\mathrm {L} }{dx}}+\beta {\frac {d\mathrm {M} }{dy}}+\gamma {\frac {d\mathrm {N} }{dz}}\cdot$

Enfin nous trouverons pour ${\frac {d^{2}\xi }{dt^{2}}},$

${\frac {d^{2}\xi }{dt^{2}}}=-\mu ^{2}\mathrm {V} ^{2}\mathrm {L} e^{\mathrm {P} }.$

En portant ces valeurs de ${\frac {d\Theta }{dx}},$ $\Delta \xi ,$ ${\frac {d^{2}\xi }{dt^{2}}}$ dans la première des équations (1) cette équation devient :

(5)

$\;\;-\mu ^{2}\mathrm {V} ^{2}\rho \mathrm {L} =\Delta \mathrm {L} -{\frac {d\mathrm {T} }{dx}}+i\mu \left(2{\frac {d\mathrm {L} }{dn}}\!-\!\alpha \mathrm {T} \!-\!{\frac {d\mathrm {Q} }{dx}}\right)-\mu ^{2}\left(\mathrm {L} \!-\!\alpha \mathrm {Q} \right).$

Si on néglige les termes qui contiennent en facteur les puissances de $\mu ,$ cette équation se réduit à

(6)

$\Delta \mathrm {L} -{\frac {d\mathrm {T} }{dx}}=0.$

169. On peut mettre cette équation et les deux qu’on déduirait de la même manière des deux dernières équations du mouvement sous une autre forme en introduisant les quantités $l,\,m,\,n$ définies par les relations suivantes

(I)

$\left\{{\begin{aligned}l&={\frac {d\mathrm {N} }{dy}}-{\frac {d\mathrm {M} }{dz}},\\[1.25ex]m&={\frac {d\mathrm {L} }{dz}}-{\frac {d\mathrm {N} }{dx}},\\[1.25ex]n&={\frac {d\mathrm {M} }{dx}}-{\frac {d\mathrm {L} }{dy}}\cdot \\\end{aligned}}\right.$

En effet si nous développons l’équation (6), elle devient

${\frac {d^{2}\mathrm {L} }{dx^{2}}}+{\frac {d^{2}\mathrm {L} }{dy^{2}}}+{\frac {d^{2}\mathrm {L} }{dz^{2}}}-{\frac {d^{2}\mathrm {L} }{dx^{2}}}-{\frac {d^{2}\mathrm {M} }{dx\,dy}}-{\frac {d^{2}\mathrm {N} }{dx\,dz}}=0,$

ou

${\frac {d^{2}\mathrm {L} }{dy^{2}}}-{\frac {d^{2}\mathrm {M} }{dx\,dy}}+{\frac {d^{2}\mathrm {L} }{dz^{2}}}-{\frac {d^{2}\mathrm {N} }{dx\,dz}}=0.$

Mise sous cette forme, il est facile de voir que cette équation n’est autre que la suivante

$-{\frac {dn}{dy}}+{\frac {dm}{dx}}=0.$

Par conséquent les trois équations du mouvement nous donneront le groupe d’équations

(II)

$\left\{{\begin{aligned}{\frac {d{n}}{dy}}-{\frac {d{m}}{dz}}&=0,\\[1.5ex]{\frac {d{l}}{dz}}-{\frac {d{n}}{dx}}&=0,\\[1.5ex]{\frac {d{m}}{dx}}-{\frac {d{l}}{dy}}&=0.\\\end{aligned}}\right.$

dont chacune est formée avec $l,\,m,\,n,$ de la même manière que ces quantités sont formées avec $\mathrm {L,\,M,\,N} .$

De l’équation (5) nous pouvons tirer une relation entre les valeurs moyennes des quantités qui y entrent. $\mathrm {L,\,M}$ et $\mathrm {N}$ étant des fonctions périodiques, et la valeur moyenne de la dérivée d’une fonction périodique étant nulle, nous aurons

$\mathrm {V} ^{2}\left[\rho \mathrm {L} \right]_{0}=\left[\mathrm {L} -\alpha \mathrm {Q} \right]_{0},$

les quantités affectées d’un indice 0 représentant les valeurs moyennes de ces quantités. En remplaçant $\mathrm {Q}$ par sa valeur (4) et en écrivant immédiatement les deux équations analogues à la précédente qui s’en déduisent par permutation, on obtient un nouveau groupe de relations :

(III)

$\left\{{\begin{aligned}\mathrm {V} ^{2}\left[\rho \mathrm {L} \right]_{0}&=\mathrm {L} _{0}-\alpha \left(\alpha \mathrm {L} _{0}+\beta \mathrm {M} _{0}+\gamma \mathrm {N} _{0}\right)\\[1.5ex]\mathrm {V} ^{2}\left[\rho \mathrm {M} \right]_{0}&=\mathrm {M} _{0}-\beta \left(\alpha \mathrm {L} _{0}+\beta \mathrm {M} _{0}+\gamma \mathrm {N} _{0}\right)\\[1.5ex]\mathrm {V} ^{2}\left[\rho \mathrm {N} \right]_{0}&=\mathrm {N} _{0}-\gamma \left(\alpha \mathrm {L} _{0}+\beta \mathrm {M} _{0}+\gamma \mathrm {N} _{0}\right)\\\end{aligned}}\right.$

Enfin les équations (1) du mouvement nous donnent une dernière relation. Nous en tirons en dérivant respectivement chacune d’elles par rapport à $x,\,y,\,z$ et additionnant

${\begin{aligned}{\frac {d}{dx}}\rho {\frac {d^{2}\xi }{dt^{2}}}+{\frac {d}{dy}}\rho {\frac {d^{2}\eta }{dt^{2}}}+{\frac {d}{dz}}\rho {\frac {d^{2}\zeta }{dt^{2}}}=\Delta &\left({\frac {d\xi }{dx}}+{\frac {d\eta }{dy}}+{\frac {d\zeta }{dz}}\right)\\&-{\frac {d^{2}\Theta }{dx^{2}}}-{\frac {d^{2}\Theta }{dy^{2}}}-{\frac {d^{2}\Theta }{dz^{2}}},\\\end{aligned}}$

ou, puisque le second membre est identiquement nul

${\frac {d}{dx}}\rho {\frac {d^{2}\xi }{dt^{2}}}+{\frac {d}{dy}}\rho {\frac {d^{2}\eta }{dt^{2}}}+{\frac {d}{dz}}\rho {\frac {d^{2}\zeta }{dt^{2}}}=0.$

Or, pour les valeurs de $\xi ,\,\eta ,\,\zeta$ définies par les relations (2), on a

${\frac {d^{2}\xi }{dt^{2}}}=-\mu ^{2}\mathrm {V} ^{2}\mathrm {L} e^{\mathrm {P} }\,;$

par conséquent l’identité précédente peut s’écrire

${\frac {d}{dx}}\rho \mathrm {L} e^{\mathrm {P} }+{\frac {d}{dy}}\rho \mathrm {M} e^{\mathrm {P} }+{\frac {d}{dz}}\rho \mathrm {N} e^{\mathrm {P} }=0,$

ou

$e^{\mathrm {P} }\left({\frac {d}{dx}}\rho \mathrm {L} +{\frac {d}{dy}}\rho \mathrm {M} +{\frac {d}{dz}}\rho \mathrm {N} \right)+i\mu \rho e^{\mathrm {P} }\left(\alpha \mathrm {L} +\beta \mathrm {M} +\gamma \mathrm {N} \right)=0.$

Si, comme nous l’avons dit, nous négligeons les termes contenant $\mu ,$ nous aurons simplement

(IV)

${\frac {d}{dx}}\rho \mathrm {L} +{\frac {d}{dy}}\rho \mathrm {M} +{\frac {d}{dz}}\rho \mathrm {N} =0.$

Nous avons donc pour déterminer $\mathrm {V} ,$ les fonctions $\mathrm {L,\,M,\,N}$ et les valeurs moyennes de ces fonctions, les trois groupes d’équations (I) (II) (III) et l’identité (IV). Au premier abord le problème semble indéterminé, puisque la fonction $\rho$ est inconnue. Nous verrons cependant qu’il peut être résolu si on ne cherche que les quantités susceptibles d’une mesure expérimentale ; mais auparavant nous allons établir deux propriétés des fonctions périodiques qui nous permettront de démontrer la périodicité des quantités $l,\,m,\,n,$ et de déterminer les valeurs de ces quantités.

170. Propriétés des fonctions périodiques. — 1^o Si $u$ et $v$ sont deux fonctions périodiques de $z,$ on a la relation suivante entre les valeurs moyennes

$\left[u\,{\frac {dv}{dz}}\right]_{0}=-\left[v\,{\frac {du}{dz}}\right]_{0}\cdot$

En effet, le produit $uv$ de deux fonctions périodiques est une fonction périodique ; par conséquent, la valeur moyenne de la dérivée de ce produit sera nulle. On a donc

$\left[u\,{\frac {dv}{dz}}+v\,{\frac {du}{dz}}\right]_{0}=0,$

ou

$\left[u\,{\frac {dv}{dz}}\right]_{0}+\left[v\,{\frac {du}{dz}}\right]_{0}=0,$

puisque la valeur moyenne d’une somme est égale à la somme des valeurs moyennes des parties qui la composent.

2^o Si $\rho$ et $\varphi$ sont deux fonctions périodiques de $x,\,y,\,z,$ satisfaisant à

${\frac {d}{dx}}\rho \,{\frac {d\varphi }{dx}}+{\frac {d}{dy}}\rho \,{\frac {d\varphi }{dy}}+{\frac {d}{dz}}\rho \,{\frac {d\varphi }{dz}}=0,$

la fonction $\varphi$ doit se réduire à une constante.

En effet, d’après la propriété précédente ou a

$\left[\varphi {\frac {d}{dx}}\rho \,{\frac {d\varphi }{dx}}\right]_{0}=-\left[\rho \,{\frac {d\varphi }{dx}}{\frac {d\varphi }{dx}}\right]_{0},$

et par conséquent

${\begin{aligned}&\left[\varphi \left({\frac {d}{dx}}\rho {\frac {d\varphi }{dx}}+{\frac {d}{dy}}\rho {\frac {d\varphi }{dy}}+{\frac {d}{dz}}\rho {\frac {d\varphi }{dz}}\right)\right]_{0}\\[1ex]&\qquad \qquad \qquad \qquad =-\left[\rho \left(\left({\frac {d\varphi }{dx}}\right)^{2}+\left({\frac {d\varphi }{dy}}\right)^{2}+\left({\frac {d\varphi }{dz}}\right)^{2}\right)\right]_{0}\cdot \end{aligned}}$

Mais par suite de notre hypothèse, le premier membre de cette égalité est égal à et on a

$\left[\rho \left(\left({\frac {d\varphi }{dx}}\right)^{2}+\left({\frac {d\varphi }{dy}}\right)^{2}+\left({\frac {d\varphi }{dz}}\right)^{2}\right)\right]_{0}=0.$

Si $\rho$ est positif, la quantité entre crochets est le produit de deux quantités positives et sa valeur moyenne doit être positive ; elle ne peut donc être nulle comme l’exige l’égalité précédente, que si

$\left({\frac {d\varphi }{dx}}\right)^{2}+\left({\frac {d\varphi }{dy}}\right)^{2}+\left({\frac {d\varphi }{dz}}\right)^{2}=0,$

ce qui exige que chacun des termes soit nul, c’est-à-dire,

${\frac {d\varphi }{dx}}={\frac {d\varphi }{dy}}={\frac {d\varphi }{dz}}=0.$

Or, cette suite d’égalités n’est vérifiée que si $\varphi$ est une constante.

Remarquons que si on fait $\rho =1$ dans la relation qui, par hypothèse, lie les fonctions $\rho$ et $\varphi ,$ cette relation devient $\Delta \varphi =0.$ Par conséquent, si une fonction périodique $\varphi$ est telle que l’on ait $\Delta \varphi =0,$ cette fonction se réduit à une constante.

171. Valeurs des quantités $l,\,m,\,n.$ — Le groupe d’équations (II) exprime que

$l\,dx+m\,dy+n\,dz$

est une différentielle exacte. Si nous désignons par $\varphi$ la fonction dont cette quantité est la différentielle, nous aurons

$l={\frac {d\varphi }{dx}},\qquad m={\frac {d\varphi }{dy}},\qquad n={\frac {d\varphi }{dz}}\cdot$

En dérivant la première des équations du groupe (I) par rapport à $x,$ la seconde, par rapport à $y,$ et la troisième, par rapport à $z,$ puis additionnant, nous obtiendrons

${\frac {dl}{dx}}+{\frac {dm}{dy}}+{\frac {dn}{dz}}=0,$

ou, en remplaçant $l,\,m,\,n$ par les expressions précédentes,

${\frac {d^{2}\varphi }{dx^{2}}}+{\frac {d^{2}\varphi }{dy^{2}}}+{\frac {d^{2}\varphi }{dz^{2}}}=\Delta \varphi =0.$

Montrons que $\varphi$ est une fonction périodique. $\mathrm {L,\,M,\,N}$ étant, par hypothèse, des fonctions périodiques, $l,\,m,\,n$ seront, d’après les équations (I) des fonctions périodiques ayant pour valeur moyenne zéro ; par conséquent, les dérivées partielles de la fonction $\varphi$ seront de la forme

${\begin{aligned}{\frac {d\varphi }{dx}}&=\sum \mathrm {A} \sin(ax+by+cz+d)=\sum \mathrm {A} \sin \theta ,\\[1.5ex]{\frac {d\varphi }{dy}}&=\sum \mathrm {B} \sin(ax+by+cz+d)=\sum \mathrm {B} \sin \theta ,\\[1.5ex]{\frac {d\varphi }{dz}}&=\sum \mathrm {C} \sin(ax+by+cz+d)=\sum \mathrm {C} \sin \theta .\\\end{aligned}}$

En dérivant la première de ces égalités par rapport à $y$ et la seconde par rapport à $x,$ nous obtenons deux expressions de la même quantité ${\frac {d^{2}\varphi }{dx\,dy}}\,;$ ces deux expressions doivent être identiques. On a donc identiquement

$\sum \mathrm {A} b\cos \theta =\sum \mathrm {B} a\cos \theta ,$

et par conséquent,

$\mathrm {A} b=\mathrm {B} a.$

On obtiendrait d’une manière analogue

$\mathrm {A} c=\mathrm {C} a\,;$

nous avons donc

${\frac {\mathrm {A} }{a}}={\frac {\mathrm {B} }{b}}={\frac {\mathrm {C} }{c}}=\mathrm {D} ,$

et par suite,

$d\varphi =\sum \mathrm {D} (a\,dx+b\,dy+c\,dz)\sin \theta =\sum \mathrm {D} \,\sin \theta \,d\theta .$

En intégrant nous aurons

$\varphi =-\sum \mathrm {D} \,\cos \theta +\mathrm {C} ^{te}$

$\varphi$ est donc une fonction périodique, et puisqu’elle satisfait à $\Delta \varphi =0,$ elle doit, d’après la propriété des fonctions périodiques précédemment démontrée, se réduire à une constante. Il en résulte que $l,\,m,\,n$ qui sont les dérivées partielles de $\varphi$ ont pour valeur 0.

172. Recherche des quantités $\mathrm {L,\,M,\,N} .$ — Puisque les quantités $l,\,m,\,n$ sont nulles, le groupe d’équations (I) nous donne les relations

${\frac {d\mathrm {N} }{dy}}-{\frac {d\mathrm {M} }{dz}}=0,\quad {\frac {d\mathrm {L} }{dz}}-{\frac {d\mathrm {N} }{dx}}=0,\quad {\frac {d\mathrm {M} }{dx}}-{\frac {d\mathrm {L} }{dy}}=0,$

qui expriment que

$\mathrm {L} \,dx+\mathrm {M} \,dy+\mathrm {N} \,dz$

est une différentielle exacte. En désignant par $\psi$ la fonction dont cette quantité est la différentielle exacte, nous aurons

(1)

$\mathrm {L} \,dx+\mathrm {M} \,dy+\mathrm {N} \,dz=d\psi ,$

équation qui peut remplacer les groupes (I) et (II). Si l’on connaissait cette fonction $\psi$ on en déduirait immédiatement les valeurs de $\mathrm {L,\,M,\,N} ,$ qui sont les dérivées partielles de $\psi$ par rapport à $x,\,y,\,z.$ Nous allons montrer que, pour des valeurs données des valeurs moyennes $\mathrm {L} _{0},\,\mathrm {M} _{0},\,\mathrm {N} _{0}$ de $\mathrm {L,\,M,\,N} ,$ il existe une fonction $\psi$ satisfaisant aux conditions imposées par les hypothèses de M. Sarrau et qu’il n’en existe qu’une en négligeant la constante d’intégration.

Remarquons que $\mathrm {L} _{0},\,\mathrm {M} _{0},\,\mathrm {N} _{0}$ étant des constantes,

$\mathrm {L} _{0}\,dx+\mathrm {M} _{0}\,dy+\mathrm {N} _{0}\,dz,$

est une différentielle exacte. Par conséquent on a

(2)

$(\mathrm {L} -\mathrm {L} _{0})\,dx+(\mathrm {M} -\mathrm {M} _{0})\,dy+(\mathrm {N} -\mathrm {N} _{0})\,dz=d\chi ,$

$d\chi$ représentant la différentielle d’une certaine fonction $\chi$ qui doit être périodique. En effet, les dérivées partielles $\mathrm {L} -\mathrm {L} _{0},$ $\mathrm {M} -\mathrm {M} _{0},$ $\mathrm {N} -\mathrm {N} _{0},$ de cette fonction sont des fonctions périodiques puisque, par hypothèse, $\mathrm {L,\,M,\,N}$ sont périodiques ; de plus la valeur moyenne de chacune de ces dérivées est évidemment nulle. La fonction $\chi$ doit donc être périodique.

L’intégration des équations (1) et (2) donne

$\psi =\mathrm {L} _{0}x+\mathrm {M} _{0}y+\mathrm {N} _{0}z+\chi \,;$

relation qui nous montre que, si à des valeurs données de $\mathrm {L_{0},\,M_{0},\,N_{0}}$ correspondent plusieurs fonctions $\psi ,$ ces fonctions ne peuvent différer entre elles que par la partie périodique $\chi .$ Par conséquent, pour démontrer qu’il ne peut exister qu’une fonction $\psi$ il nous suffit de démontrer qu’il ne peut y avoir qu’une seule fonction périodique $\chi .$

Pour cette démonstration considérons l’équation (IV). En y remplaçant $\mathrm {L,\,M,\,N}$ par ${\frac {d\psi }{dx}},\,{\frac {d\psi }{dy}},\,{\frac {d\psi }{dz}},$ elle devient :

(3)

${\frac {d}{dx}}\rho \,{\frac {d\psi }{dx}}+{\frac {d}{dy}}\rho \,{\frac {d\psi }{dy}}+{\frac {d}{dz}}\rho \,{\frac {d\psi }{dz}}=0.$

Si nous admettons qu’il existe deux fonctions $\psi _{1}$ et $\psi _{2}$ satisfaisant à cette équation, la différence $\psi _{1}-\psi _{2}$ devra également y satisfaire. Or cette différence est une fonction périodique égale, d’après ce qui précède, à la différence $\chi _{1}-\chi _{2}$ des parties périodiques des fonctions $\psi _{1}$ et $\psi _{2}\,;$ elle doit donc se réduire à une constante. Par conséquent les deux fonctions $\psi _{1}$ et $\psi _{2}$ ne diffèrent que par une constante.

173. Montrons qu’il existe une fonction $\psi$ satisfaisant à la relation (3).

Considérons la fonction

$\rho (\mathrm {L} ^{2}+\mathrm {M} ^{2}+\mathrm {N} ^{2}).$

Sa valeur moyenne est essentiellement positive puisque $\rho$ est une quantité positive et le second facteur une somme de carrés. En outre elle ne peut devenir nulle, car il faudrait que l’on eût $\mathrm {L=M=N=0} ,$ ce qui est impossible puisque les valeurs moyennes $\mathrm {L_{0},\,M_{0},\,N_{0}}$ qui sont données ne sont pas nulles en général. Cette valeur moyenne doit donc passer par un minimum auquel correspond une certaine valeur de la fonction $\chi .$ Si nous donnons à $\chi$ un accroissement $\delta \chi$ les accroissements $\delta \mathrm {L} ,$ $\delta \mathrm {M} ,$ $\delta \mathrm {N}$ de $\mathrm {L,\,M,\,N}$ satisfont en vertu des propriétés des minimums à la relation

(4)

${\big [}\rho \left(\mathrm {L} \,\delta \mathrm {L} +\mathrm {M} \,\delta \mathrm {M} +\mathrm {N} \,\delta \mathrm {N} \right){\big ]}_{0}=0.$

Or, la valeur de $\psi$

$\psi =\mathrm {L} _{0}x+\mathrm {M} _{0}y+\mathrm {N} _{0}z+\chi ,$

donne :

$\delta \psi =\delta \chi .$

Par conséquent on aura

${\begin{aligned}\delta \mathrm {L} &={\frac {d}{dx}}\,\delta \chi ,&\delta \mathrm {M} &={\frac {d}{dy}}\,\delta \chi ,&\delta \mathrm {N} &={\frac {d}{dz}}\,\delta \chi ,\end{aligned}}$

et par suite.

${\begin{aligned}{\Big [}\rho \mathrm {L} \,\delta \mathrm {L} {\Big ]}_{0}&=\left[\rho \mathrm {L} \,{\frac {d}{dx}}\delta \chi \right]_{0},\\[1.5ex]{\Big [}\rho \mathrm {M} \,\delta \mathrm {M} {\Big ]}_{0}&=\left[\rho \mathrm {M} \,{\frac {d}{dy}}\delta \chi \right]_{0},\\[1.5ex]{\Big [}\rho \mathrm {N} \,\delta \mathrm {N} {\Big ]}_{0}&=\left[\rho \mathrm {N} \,{\frac {d}{dz}}\delta \chi \right]_{0}\cdot \end{aligned}}$

En additionnant ces relations membre à membre on obtient une égalité dont le premier membre est nul d’après la relation(4) ; on a donc

$\left[\rho \mathrm {L} {\frac {d}{dx}}\delta \chi \right]_{0}+\left[\rho \mathrm {M} {\frac {d}{dy}}\delta \chi \right]_{0}+\left[\rho \mathrm {N} {\frac {d}{dz}}\delta \chi \right]_{0}=0.$

Si nous transformons chacun des termes de cette égalité en nous appuyant sur la propriété des fonctions périodiques démontrée précédemment (170), nous obtiendrons

$\left[\delta \chi {\frac {d}{dx}}\rho \mathrm {L} \right]_{0}+\left[\delta \chi {\frac {d}{dy}}\rho \mathrm {M} \right]_{0}+\left[\delta \chi {\frac {d}{dz}}\rho \mathrm {N} \right]_{0}=0.$

Cette égalité devant être satisfaite quelle que soit la valeur donnée à $\delta \chi ,$ on doit avoir

(5)

${\frac {d}{dx}}\rho \mathrm {L} +{\frac {d}{dy}}\rho \mathrm {M} +{\frac {d}{dz}}\rho \mathrm {N} =0.$

Il existe donc une fonction $\chi ,$ et par suite, une fonction $\psi ,$ telles que les valeurs de $\mathrm {L,\,M,\,N} ,$ qui s’en déduisent satisfont à l’équation précédente.

Il est facile de démontrer que si

${\begin{array}{crrcl}\mathrm {pour} &\mathrm {L} _{0}=1,&\mathrm {M} _{0}=\mathrm {N} _{0}=0&\mathrm {on~a} &\psi =\psi _{1},\\[1.25ex]&\mathrm {M} _{0}=1,&\mathrm {L} _{0}=\mathrm {N} _{0}=0&&\psi =\psi _{2},\\[1.25ex]&\mathrm {N} _{0}=1,&\mathrm {M} _{0}=\mathrm {L} _{0}=0&&\psi =\psi _{3},\\\end{array}}$

la forme la plus générale de la fonction $\psi$ sera

$\psi =\mathrm {L} _{0}\psi _{1}+\mathrm {M} _{0}\psi _{2}+\mathrm {N} _{0}\psi _{3}.$

En effet, puisque $\psi _{1},\,\psi _{2},\,\psi _{3}$ satisfont à l’équation (5), la fonction $\psi$ doit y satisfaire également. De plus les valeurs moyennes des dérivées partielles de $\psi$ sont bien égales à $\mathrm {L_{0},\,M_{0},\,N_{0}.}$ car on a

$\left[{\frac {d\psi }{dx}}\right]_{0}=\mathrm {L} _{0}\left[{\frac {d\psi _{1}}{dx}}\right]_{0}+\mathrm {M} _{0}\left[{\frac {d\psi _{2}}{dx}}\right]_{0}+\mathrm {N} _{0}\left[{\frac {d\psi _{3}}{dx}}\right]_{0}=\mathrm {L} _{0},$

puisque par hypothèse

$\left[{\frac {d\psi _{1}}{dx}}\right]_{0}=1,\quad \left[{\frac {d\psi _{2}}{dx}}\right]_{0}=0,\quad \left[{\frac {d\psi _{3}}{dx}}\right]_{0}=0.$

On verrait de la même manière que les valeurs moyennes des

dérivées partielles par rapport à $y$ et à $z$ sont respectivement

$\mathrm {M} _{0}$ et $\mathrm {N} _{0}.$

174. Valeurs des vitesses de propagation. — La relation,

$\psi =\mathrm {L} _{0}x+\mathrm {M} _{0}y+\mathrm {N} _{0}z+\chi$

nous montre que $\psi$ dépend linéairement de $\mathrm {L_{0},\,M_{0},\,N_{0}} \,;$ par suite il en sera de même des dérivées partielles, $\mathrm {L,\,M,\,N} ,$ de cette fonction. La fonction $\rho \,(\mathrm {L^{2}+M^{2}+N^{2}} )$ et sa valeur moyenne seront donc des fonctions homogènes du second degré de $\mathrm {L_{0},\,M_{0},\,N_{0}} .$ Par un choix convenable des axes de coordonnées, que jusqu’ici nous avons laissés arbitraires, nous pourrons faire disparaître les termes rectangles de la valeur moyenne et nous aurons

${\frac {\mathrm {L} _{0}^{2}}{a}}+{\frac {\mathrm {M} _{0}^{2}}{b}}+{\frac {\mathrm {N} _{0}^{2}}{c}}={\Big [}\rho \left(\mathrm {L^{2}+M^{2}+N^{2}} \right){\Big ]}_{0}$

Si nous donnons à $\mathrm {L} _{0}$ un accroissement $\delta \mathrm {L} _{0}$ il en résultera un accroissement ${\frac {2\mathrm {L} _{0}\,\delta \mathrm {L} _{0}}{a}}$ de la valeur moyenne de $\rho (\mathrm {L^{2}+M^{2}+N^{2}} ).$ Or, cet accroissement a également pour valeur

$2{\Big [}\rho \left(\mathrm {L} \,\delta \mathrm {L} +\mathrm {M} \,\delta \mathrm {M} +\mathrm {N} \,\delta \mathrm {N} \right){\Big ]}_{0}\,;$

comme on a

${\begin{aligned}\delta \psi &=\delta \chi +x\,\delta \mathrm {L} _{0},\\\delta \mathrm {L} &={\frac {d}{dx}}\,\delta \chi +\delta \mathrm {L} _{0},\\\delta \mathrm {M} &={\frac {d}{dy}}\,\delta \chi ,\\\delta \mathrm {N} &={\frac {d}{dz}}\,\delta \chi ,\\\end{aligned}}$

la dernière expression de l’accroissement de la valeur moyenne de $\rho \,(\mathrm {L^{2}+M^{2}+N^{2}} )$ devient

$2{\bigg [}\rho \mathrm {L} \,\delta \mathrm {L} _{0}{\bigg ]}_{0}+2{\bigg [}\rho \left(\mathrm {L} {\frac {d}{dx}}\delta \chi +\mathrm {M} {\frac {d}{dy}}\delta \chi +\mathrm {N} {\frac {d}{dz}}\delta \chi \right){\bigg ]}_{0}\cdot$

Le second terme de cette somme est nul puisque la relation (5) doit être satisfaite. Par conséquent, en égalant les deux valeurs de l’accroissement, on obtient

${\frac {\mathrm {L} _{0}\,\delta \mathrm {L} _{0}}{a}}={\big [}\rho \mathrm {L} \,\delta \mathrm {L} _{0}{\big ]}_{0}=\delta \mathrm {L} _{0}\,{\big [}\rho \mathrm {L} {\big ]}_{0}\,;$

d’où

${\big [}\rho \mathrm {L} {\big ]}_{0}={\frac {\mathrm {L} _{0}}{a}}\cdot$

On aurait pour les valeurs moyennes de $\rho \mathrm {M}$ et de $\rho \mathrm {N}$ les quantités ${\frac {\mathrm {M} _{0}}{b}},$ ${\frac {\mathrm {N} _{0}}{c}}\cdot$ En portant ces quantités dans les équations du groupe (III), ces équations deviennent

(V)

${\begin{aligned}{\frac {\mathrm {V} ^{2}\mathrm {L} _{0}}{a}}=\mathrm {L} _{0}-\alpha (\alpha \mathrm {L} _{0}+\beta \mathrm {M} _{0}+\gamma \mathrm {N} _{0}),\\[1.5ex]{\frac {\mathrm {V} ^{2}\mathrm {M} _{0}}{b}}=\mathrm {M} _{0}-\beta (\alpha \mathrm {L} _{0}+\beta \mathrm {M} _{0}+\gamma \mathrm {N} _{0}),\\[1.5ex]{\frac {\mathrm {V} ^{2}\mathrm {N} _{0}}{c}}=\mathrm {N} _{0}-\gamma (\alpha \mathrm {L} _{0}+\beta \mathrm {M} _{0}+\gamma \mathrm {N} _{0}),\\\end{aligned}}$

d’où nous pourrons tirer des quantités proportionnelles à $\mathrm {L_{0},\,M_{0},\,N_{0}} .$

Les périodes de $\mathrm {L,\,M,\,N}$ étant très courtes, les valeurs moyennes de ces quantités interviendront seules dans les expériences. Donc tout se passera comme si les vibrations avaient une direction constante dont les cosinus directeurs seraient proportionnels à $\mathrm {L_{0},\,M_{0},\,N_{0}} .$ Nous n’aurons donc, pour la recherche des conséquences expérimentales de la théorie de M. Sarrau, qu’à considérer le groupe d’équations qui précède. II est facile de les mettre sous une forme déjà connue en posant

(6)

$\mathrm {L} _{0}=\mathrm {A} a,\qquad \mathrm {M} _{0}=\mathrm {B} b,\qquad \mathrm {N} _{0}=\mathrm {C} c,$

et

$\mathrm {H} =\mathrm {A} a\alpha +\mathrm {B} b\beta +\mathrm {C} c\gamma \,;$

nous obtenons alors

(VI)

${\begin{aligned}\mathrm {V^{2}A} &=a\mathrm {A} -\alpha \mathrm {H} ,\\[1.25ex]\mathrm {V^{2}B} &=b\mathrm {B} -\beta \mathrm {H} ,\\[1.25ex]\mathrm {V^{2}C} &=c\mathrm {C} -\gamma \mathrm {H} .\\\end{aligned}}$

Ce sont les équations que nous avons déduites des hypothèses de Fresnel ; elles conduisent à l’équation suivante :

${\frac {\alpha ^{2}}{\mathrm {V} ^{2}-a}}+{\frac {\beta ^{2}}{\mathrm {V} ^{2}-b}}+{\frac {\gamma ^{2}}{\mathrm {V} ^{2}-c}}=0$

qui donne les vitesses de propagation d’une onde plane.

175. Direction des vibrations d’une onde plane. — Si $\mathrm {A,\,B,\,C}$ sont les composantes de la vibration de Fresnel celles de la vibration de M. Sarrau seront, d’après les relations (6),

$\mathrm {A} a,\qquad \mathrm {B} b,\qquad \mathrm {C} c.$

Désignons les composantes de la vibration de Neumann par $\mathrm {A',\,B',\,C'} \,;$ nous savons qu’il existe entre $\mathrm {A,\,B,\,C} ,$ $\mathrm {A',\,B',\,C'} ,$ $\alpha ,\,\beta ,\,\gamma$ les trois relations

${\begin{aligned}\mathrm {A} \;\alpha \,+\mathrm {B} \;\beta +\mathrm {C} \,\gamma &=0,\\\mathrm {A} '\,\alpha +\mathrm {B} '\,\beta +\mathrm {C} '\gamma &=0,\\\mathrm {AA'} +\mathrm {BB'} +\mathrm {CC'} &=0.\\\end{aligned}}$

Les deux premières expriment que les vibrations de Fresnel et de Neumann sont dans le plan de l’onde, la troisième que ces deux vibrations sont rectangulaires. Elles vont nous permettre de trouver la direction de la vibration d’après M. Sarrau.

Multiplions les équations (VI) par $\mathrm {A',\,B',\,C'}$ et additionnons ; nous aurons

$\mathrm {V} ^{2}\sum \mathrm {AA'} =\sum a\mathrm {AA'} -\mathrm {H} \sum \alpha \mathrm {A'} ,$

équation qui d’après les relations précédentes se réduit à

$\mathrm {A'A} a+\mathrm {B'B} b+\mathrm {C'C} c=0.$

Cette dernière relation montre que la vibration de M. Sarrau est perpendiculaire à celle de Neumann. Comme en général la vibration de M. Sarrau ne se confond pas en direction avec celle de Fresnel puisque dans les corps anisotropes, $a,\,b,\,c$ ont des valeurs différentes, elle n’est pas située dans le plan de l’onde ; nous verrons bientôt qu’elle est perpendiculaire au rayon lumineux. Dans le cas des corps isotropes, $a,\,b,\,c$ deviennent égaux et la vibration de M. Sarrau ayant alors la même direction que celle de Fresnel se trouve dans le plan de l’onde.

Les théories de Fresnel, de Neumann, de M. Sarrau conduisent donc à la même équation pour la vitesse de propagation ; elles ne diffèrent que par la direction de la vibration. En outre dans les milieux isotropes elles donnent pour cette direction soit celle de l’intersection du plan de polarisation et du plan de l’onde, soit celle de la normale au plan de polarisation contenue dans le plan de l’onde. Les observations ne pouvant être faites que dans l’air, milieu qui jouit de l’isotropie, l’expérience ne pourra indiquer laquelle de ces trois théories doit être définitivement acceptée.

THÉORIE DE M. BOUSSINESQ

176. Équations du mouvement. — Nous avons, à propos de la dispersion, exposé les hypothèses particulières à M. Boussinesq et nous avons vu que les équations du mouvement d’une molécule d’éther sont :

$\rho \,{\frac {d^{2}\xi }{dt^{2}}}=\Delta \xi -{\frac {d\Theta }{dx}}-\rho _{1}{\frac {d^{2}\xi _{1}}{dt^{2}}},$

et les deux qui se déduisent de celle-ci par permutation. Dans ces équations $\rho$ est la densité de l’éther, $\rho _{1}$ celle de la matière au point considéré ; $\xi ,\,\eta ,\,\zeta$ les composantes du déplacement de la molécule d’éther ; $\xi _{1},\,\eta _{1},\,\zeta _{1},$ celles du déplacement de la molécule matérielle. Ces dernières quantités doivent dépendre du déplacement et de la vitesse de la molécule d’éther, c’est-à-dire de $\xi ,\,\eta ,\,\zeta$ et de leurs dérivées. Lorsque nous voulions expliquer la dispersion nous avons dû tenir compte de ces dérivées, mais dans la théorie de la double réfraction on peut les négliger et considérer $\xi _{1},\,\eta _{1},\,\zeta _{1}$ comme des fonctions de $\xi ,\,\eta ,\,\zeta ,$ seulement. D’ailleurs, comme $\xi ,\,\eta ,\,\zeta ,$ sont des quantités très petites on peut, avec une approximation très suffisante, prendre pour $\xi _{1},\,\eta _{1},\,\zeta _{1},$ les termes du premier degré des développements de ces fonctions par rapport à $\xi ,\,\eta ,\,\zeta .$ Les composantes du déplacement d’une molécule matérielle seront alors des fonctions linéaires des composantes du déplacement de la molécule d’éther et pour un système d’axes de coordonnées convenablement choisi on aura

$\xi _{1}=h\xi ,\qquad \eta _{1}=k\eta ,\qquad \zeta _{1}=l\zeta .$

En substituant ces valeurs dans les équations du mouvement nous obtiendrons

$(\rho +\rho _{1})h\,{\frac {d^{2}\xi }{dt^{2}}}=\Delta x-{\frac {d\Theta }{dx}},$

et deux équations analogues. Si nous posons

${\begin{aligned}\rho +\rho _{1}h&={\frac {1}{a}},&\rho +\rho _{1}k&={\frac {1}{b}},&\rho +\rho _{1}l&={\frac {1}{c}},\end{aligned}}$

elles deviendront

(1)

${\begin{aligned}{\frac {1}{a}}{\frac {d^{2}\xi }{dt^{2}}}&=\Delta \xi -{\frac {d\Theta }{dx}},\\[1.5ex]{\frac {1}{b}}{\frac {d^{2}\eta }{dt^{2}}}&=\Delta \eta -{\frac {d\Theta }{dy}},\\[1.5ex]{\frac {1}{c}}{\frac {d^{2}\zeta }{dt^{2}}}&=\Delta \zeta -{\frac {d\Theta }{dz}}\cdot \\\end{aligned}}$

177. Propagation d’une onde plane. — Soient $\xi ,\,\eta ,\,\zeta$ les composantes des vibrations d’une onde plane ; nous pouvons poser

(2)

${\begin{aligned}\xi &=\mathrm {L} _{0}e^{\mathrm {P} },&\eta &=\mathrm {M} _{0}e^{\mathrm {P} },&\zeta &=\mathrm {N} _{0}e^{\mathrm {P} }.\end{aligned}}$

Si nous calculons quelles sont alors les valeurs des quantités qui entrent dans les équations (1) nous trouvons

${\begin{aligned}{\frac {d^{2}\xi }{dt^{2}}}&=-{\frac {4\pi ^{2}}{\lambda ^{2}}}\mathrm {V} ^{2}\mathrm {L} _{0}e^{\mathrm {P} },\\[1.5ex]{\frac {d\xi }{dx}}&=+{\frac {2i\pi }{\lambda }}\alpha \mathrm {L} _{0}e^{\mathrm {P} },\\[1.5ex]{\frac {d^{2}\xi }{dx^{2}}}&=-{\frac {4\pi ^{2}}{\lambda ^{2}}}\alpha ^{2}\mathrm {L} _{0}e^{\mathrm {P} },\\\end{aligned}}$

d’où nous déduisons

${\begin{aligned}\Theta &={\frac {2i\pi }{\lambda }}e^{\mathrm {P} }\,(\alpha \mathrm {L} _{0}+\beta \mathrm {M} _{0}+\gamma \mathrm {N} _{0}),\\[1.5ex]{\frac {d\Theta }{dx}}&=-{\frac {4\pi ^{2}}{\lambda ^{2}}}e^{\mathrm {P} }\alpha \,(\alpha \mathrm {L} _{0}+\beta \mathrm {M} _{0}+\gamma \mathrm {N} _{0}),\end{aligned}}$

et

$\Delta \xi ={\frac {4\pi ^{2}}{\lambda ^{2}}}\mathrm {L} _{0}e^{\mathrm {P} }.$

En portant ces valeurs de ${\frac {d^{2}\xi }{dt^{2}}},\,{\frac {d\Theta }{dx}},\,\Delta \xi$ dans la première des équations du mouvement (1), nous obtiendrons une nouvelle équation à laquelle nous joindrons les deux qui s’en déduisent et nous aurons

${\begin{aligned}{\frac {\mathrm {V^{2}L_{0}} }{a}}&=\mathrm {L} _{0}-\alpha \,(\alpha \mathrm {L} _{0}+\beta \mathrm {M} _{0}+\gamma \mathrm {N} _{0}),\\[1.5ex]{\frac {\mathrm {V^{2}M_{0}} }{b}}&=\mathrm {M} _{0}-\beta \,(\alpha \mathrm {L} _{0}+\beta \mathrm {M} _{0}+\gamma \mathrm {N} _{0}),\\[1.5ex]{\frac {\mathrm {V^{2}N_{0}} }{c}}&=\mathrm {N} _{0}-\gamma \,(\alpha \mathrm {L} _{0}+\beta \mathrm {M} _{0}+\gamma \mathrm {N} _{0}).\\\end{aligned}}$

Ces équations sont précisément celles que nous avons déduites

des hypothèses de M. Sarrau (175) ; la théorie de M. Boussinesq doit donc conduire aux mêmes conséquences que celle

de M. Sarrau.

178. Relations entre les composantes des vibrations de Fresnel, de Neumann, de M. Sarrau. — On peut donner aux équations (1) du mouvement une autre forme en posant

(I)

${\begin{aligned}\mathrm {X} &={\frac {d\zeta }{dy}}-{\frac {d\eta }{dz}},\\[1.5ex]\mathrm {Y} &={\frac {d\xi }{dz}}-{\frac {d\zeta }{dx}},\\[1.5ex]\mathrm {Z} &={\frac {d\eta }{dx}}-{\frac {d\xi }{dy}}\cdot \\\end{aligned}}$

et

(II)

${\begin{aligned}u&={\frac {d\mathrm {Z} }{dy}}-{\frac {d\mathrm {Y} }{dz}},\\[1.5ex]v&={\frac {d\mathrm {X} }{dz}}-{\frac {d\mathrm {Z} }{dx}},\\[1.5ex]w&={\frac {d\mathrm {Y} }{dx}}-{\frac {d\mathrm {X} }{dy}}\cdot \\\end{aligned}}$

La substitution dans $u,\,v,\,w$ des valeurs de $\mathrm {X,\,Y,\,Z}$ données par le groupe (I) conduit à

$u=-\Delta \xi +{\frac {d\Theta }{dx}}$

et deux égalités analogues ; par conséquent les équations (I) deviennent

(III)

${\begin{aligned}{\frac {d^{2}\xi }{dt^{2}}}&=au\\[1.5ex]{\frac {d^{2}\eta }{dt^{2}}}&=bv\\[1.5ex]{\frac {d^{2}\zeta }{dt^{2}}}&=cw\\\end{aligned}}$

Nous allons montrer que $\xi ,\,\eta ,\,\zeta$ étant les composantes de la vibration de M. Sarrau, $\mathrm {X,\,Y,\,Z}$ sont proportionnels à celles de la vibration de Neumann et $u,\,v,\,w$ à celles de la vibration de Fresnel.

Si dans $\mathrm {X,\,Y,\,Z}$ nous remplaçons les dérivées partielles de $\xi ,\,\eta ,\,\zeta$ par leurs valeurs tirées des relations (2), nous obtenons pour l’une de ces quantités $\mathrm {X} ,$

$\mathrm {X} ={\frac {2i\pi }{\lambda }}e^{\mathrm {P} }(\beta \mathrm {N} _{0}-\gamma \mathrm {M} _{0})\,;$

et si nous posons,

(3)

${\begin{aligned}\mathrm {A'} &=\beta \mathrm {N} _{0}-\gamma \mathrm {M} _{0},\\\mathrm {B'} &=\gamma \mathrm {L} _{0}-\alpha \mathrm {N} _{0},\\\mathrm {C'} &=\alpha \mathrm {M} _{0}-\beta \mathrm {L} _{0},\end{aligned}}$

nous aurons pour $\mathrm {X,\,Y,\,Z} ,$

${\begin{aligned}\mathrm {X} &={\frac {2i\pi }{\lambda }}\mathrm {A'} e^{\mathrm {P} },&\mathrm {Y} &={\frac {2i\pi }{\lambda }}\mathrm {B'} e^{\mathrm {P} },&\mathrm {Z} &={\frac {2i\pi }{\lambda }}\mathrm {C'} e^{\mathrm {P} },\end{aligned}}$

c’est-à-dire que $\mathrm {X,\,Y,\,Z}$ sont respectivement proportionnels à $\mathrm {A',\,B',\,C'} .$ Or des relations précédentes (3), nous déduisons immédiatement les deux suivantes,

${\begin{aligned}\mathrm {A} '\alpha \;+\;\mathrm {B} '\beta \;+\;\mathrm {C} '\gamma \;&=0,\\[1ex]\mathrm {A'L} _{0}+\mathrm {B'M} _{0}+\mathrm {C'N} _{0}&=0.\\\end{aligned}}$

La première exprimant qu’un déplacement ayant pour composantes $\mathrm {A',\,B',\,C'}$ appartient au plan de l’onde, la seconde que ce déplacement est perpendiculaire à la vibration de M. Sarrau, $\mathrm {A',\,B',\,C'}$ doivent d’après ce que nous savons sur les directions des vibrations de Neumann et de M. Sarrau, être proportionnels aux composantes de la vibration de Neumann. Il en est également de même de $\mathrm {X,\,Y,\,Z} .$

Considérons maintenant $u,\,v,\,w.$ Ces quantités étant formées avec $\mathrm {X,\,Y,\,Z}$ comme $\mathrm {X,\,Y,\,Z}$ le sont avec $\xi ,\,\eta ,\,\zeta ,$ nous aurons la valeur de $u$ en remplaçant dans la valeur $\mathrm {X}$ précédemment trouvée $\mathrm {X}$ par $u,$ $\mathrm {N} _{0}$ par ${\frac {2i\pi }{\lambda }}\mathrm {C} '$ et $\mathrm {M} _{0}$ par ${\frac {2i\pi }{\lambda }}\mathrm {B} '.$ Cette substitution donne

$u={\frac {2i\pi }{\lambda }}e^{\mathrm {P} }\left(\beta \,{\frac {2i\pi }{\lambda }}\,\mathrm {C} '-\gamma \,{\frac {2i\pi }{\lambda }}\,\mathrm {B} '\right).$

Nous aurons donc pour $u,\,v,\,w$

${\begin{aligned}u&=-{\frac {4\pi ^{2}}{\lambda ^{2}}}\,e^{\mathrm {P} }(\beta \mathrm {C} '-\gamma \mathrm {B} ')=-{\frac {4\pi ^{2}}{\lambda ^{2}}}\,e^{\mathrm {P} }\mathrm {A} ,\\[1.5ex]v&=-{\frac {4\pi ^{2}}{\lambda ^{2}}}\,e^{\mathrm {P} }(\gamma \mathrm {A} '-\alpha \mathrm {C} ')=-{\frac {4\pi ^{2}}{\lambda ^{2}}}\,e^{\mathrm {P} }\mathrm {B} ,\\[1.5ex]w&=-{\frac {4\pi ^{2}}{\lambda ^{2}}}\,e^{\mathrm {P} }(\alpha \mathrm {B} '-\beta \mathrm {A} ')=-{\frac {4\pi ^{2}}{\lambda ^{2}}}\,e^{\mathrm {P} }\mathrm {C} .\\\end{aligned}}$

Ces égalités montrent que les quantités $u,\,v,\,w$ sont proportionnelles aux quantités $\mathrm {A,\,B,\,C}$ définies par les relations suivantes

${\begin{aligned}\mathrm {A} =\beta \mathrm {C} '-\gamma \mathrm {B} ',\\[1ex]\mathrm {B} =\gamma \mathrm {A} '-\alpha \mathrm {C} ',\\[1ex]\mathrm {C} =\alpha \mathrm {B} '-\beta \mathrm {A} '.\\\end{aligned}}$

De ces relations on déduit facilement

${\begin{aligned}\mathrm {A} \alpha \;+\;\mathrm {B} \beta \;+\;\mathrm {C} \gamma \;&=0\,;\\[1ex]\mathrm {AA} '+\mathrm {BB} '+\mathrm {CC} '&=0.\\\end{aligned}}$

Si donc $\mathrm {A',\,B',\,C'}$ sont proportionnels aux cosinus directeurs de la vibration de Neumann, $\mathrm {A,\,B,\,C}$ et par suite $u,\,v,\,w$ seront proportionnels à ceux de la vibration de Fresnel, ces relations exprimant, la première que la direction $\mathrm {A,\,B,\,C}$ est dans le plan de l’onde, la seconde que cette direction est normale à la vibration de Neumann.

Dans la théorie électro-magnétique de la lumière on retrouve les trois groupes d’équations (I), (II), (III) ; dans cette théorie ${\frac {d\xi }{dt}},$ ${\frac {d\eta }{dt}},$ ${\frac {d\zeta }{dt}}$ sont les composantes de la force électromotrice, $x,\,y,\,z$ celles de la force magnétique et $u,\,v,\,w$ celles du déplacement électrique.

179. Changements d’axes de coordonnées. — Les équations du mouvement dans les diverses théories de la double réfraction ont été établies en prenant pour axes de coordonnées des axes particuliers, les axes de symétrie optique du milieu. Les équations du mouvement mises sous la forme (III) présentent le grand avantage de se prêter à un changement d’axes et de donner facilement les cosinus directeurs de la vibration de M. Sarrau. Les relations qui existent entre les directions des vibrations de Fresnel, de Neumann et de M. Sarrau étant indépendantes du choix des axes de coordonnées pourvu qu’ils soient rectangulaires, les groupes de relations (I) et (II) permettront toujours de trouver les cosinus directeurs des vibrations de Neumann et de Fresnel quand on connaîtra les composantes $\xi ,\,\eta ,\,\zeta$ de la vibration de M. Sarrau. Cherchons donc ce que deviennent les équations (III) quand on fait un changement d’axes.

Posons

$au^{2}+bv^{2}+cw^{2}=\mathrm {F} (u,\,v,\,w).$

Les équations (III) peuvent alors s’écrire :

(IV)

${\frac {d^{2}\xi }{dt^{2}}}=-{\frac {1}{2}}{\frac {d\mathrm {F} }{du}},\quad {\frac {d^{2}\eta }{dt^{2}}}=-{\frac {1}{2}}{\frac {d\mathrm {F} }{dv}},\quad {\frac {d^{2}\zeta }{dt^{2}}}=-{\frac {1}{2}}{\frac {d\mathrm {F} }{dw}}\cdot$

L’équation du plan tangent à l’ellipsoïde $\mathrm {F} =1$ au point $\mathrm {P}$ de coordonnées $-u,\,-v,\,-w$ est :

$\mathrm {U} {\frac {d\mathrm {F} }{du}}+\mathrm {V} {\frac {d\mathrm {F} }{dv}}+\mathrm {W} {\frac {d\mathrm {F} }{dw}}=-1$

et la distance $\mathrm {OT}$ (fig. 19) du centre $\mathrm {O}$ de l’ellipsoïde à ce plan est :

${\frac {1}{\sqrt {\displaystyle \left({\frac {d\mathrm {F} }{du}}\right)^{2}+\left({\frac {d\mathrm {F} }{dv}}\right)^{2}+\left({\frac {d\mathrm {F} }{dw}}\right)^{2}\cdot }}}$

Si donc on prend sur la droite $\mathrm {OT}$ une longueur $\mathrm {OS} ={\frac {1}{\mathrm {OT} }}$ les coordonnées du point $\mathrm {S}$ seront $-{\frac {d\mathrm {F} }{du}},$ $-{\frac {d\mathrm {F} }{dv}},$ $-{\frac {d\mathrm {F} }{dw}}$ c’est-à-dire le double de ${\frac {d^{2}\xi }{dt^{2}}},$
Fig. 19. ${\frac {d^{2}\eta }{dt^{2}}},$ ${\frac {d^{2}\zeta }{dt^{2}}}\cdot$ Le point $\mathrm {S}$ se déduisant du point $\mathrm {P}$ par une construction géométrique indépendante de la direction des axes, les valeurs de ${\frac {d^{2}\xi }{dt^{2}}},$ ${\frac {d^{2}\eta }{dt^{2}}},$ ${\frac {d^{2}\zeta }{dt^{2}}}$ auront toujours la même forme quels que soient les axes. Les équations (IV) seront toujours vraies, mais $\mathrm {F}$ aura pour expression dans le cas le plus général

$\mathrm {F} =au^{2}+bv^{2}+cw^{2}+2dvw+2ewu+2fuv.$

En développant les seconds termes des équations (IV), on obtient alors

${\begin{aligned}{\frac {d^{2}\xi }{dt^{2}}}&=-(au+fv+ew),\\[1.5ex]{\frac {d^{2}\eta }{dt^{2}}}&=-(fu+bv+dw),\\[1.5ex]{\frac {d^{2}\zeta }{dt^{2}}}&=-(eu+dv+cw)\,;\\\end{aligned}}$

ce sont les équations de la double réfraction rapportées à des axes quelconques.

SURFACE D’ONDE. — PROPAGATION RECTILIGNE DE LA LUMIÈRE.

180. Surface d’onde. — Si nous supposons l’éther primitivement au repos et qu’à l’origine des temps on ébranle les molécules contenues dans une sphère de rayon très petit, les molécules en mouvement au bout de l’unité de temps appartiendront à une certaine surface qu’on appelle surface d’onde.

Cette surface est une sphère dans un milieu isotrope. En étendant aux corps non isotropes le principe de Huyghens, on peut trouver l’équation de la surface d’onde dans ces milieux quand on connaît la vitesse de propagation d’une onde plane. Mais on peut faire à cette extension du principe de Huyghens les objections que nous avons signalées dans le cas des isotropes, et pour être rigoureux, il nous faudrait recommencer pour les corps anisotropes la justification à laquelle nous sommes parvenus dans le chapitre III. Nous nous bornerons à admettre la manière de raisonner de Huyghens sans en chercher la justification.

Considérons une onde plane $\mathrm {PP} '$ {fig. 20) passant par un
Fig. 20. point $\mathrm {O}$ d’un milieu anisotrope. Au bout de l’unité de temps, cette onde coïncidera avec le plan $\mathrm {QQ} '$ parallèle à $\mathrm {PP} ',$ et situé à une distance de ce dernier plan égale à la vitesse de propagation $\mathrm {V}$ de cette onde.

D’autre part, l’ébranlement initial du point $\mathrm {O}$ mettra en mouvement au bout du temps $\mathrm {t}$ les molécules du milieu élastique qui, d’après la définition de la surface d’onde, sont situées sur la surface d’onde $\mathrm {S}$ relative au point $\mathrm {O} .$ Or, d’après le principe de Huyghens, le mouvement de l’éther en tout point de l’onde plane $\mathrm {QQ} '$ est la résultante des mouvements qu’envoient isolément chacun des points $\mathrm {O,O} '$ de l’onde $\mathrm {PP} '.$ Les ondes élémentaires de ces points étant $\mathrm {S,\,S} ',\dots$ il ne peut y avoir de mouvement au-delà du plan tangent commun $\mathrm {Q_{1}Q_{1}'}$ à ces ondes. De plus il y en a certainement au point $\mathrm {Q} _{1}$ où ce plan $\mathrm {Q_{1}Q'}$ touche la surface $\mathrm {S} \,;$ car $\mathrm {Q} _{1}$ étant extérieur aux autres surfaces d’onde $\mathrm {S} '$ etc ; le mouvement envoyé en $\mathrm {Q} _{1}$ par le point $\mathrm {O}$ ne peut être détruit par le mouvement envoyé par les autres points du plan $\mathrm {PP} ',$ et comme le mouvement ne doit avoir lieu que dans le plan $\mathrm {QQ} ',$ les deux plans $\mathrm {QQ} '$ et $\mathrm {Q_{1}Q_{1}'}$ doivent se confondre.

Quelle que soit la direction du plan de l’onde $\mathrm {PP} '$ passant par le point $\mathrm {O} ,$ la surface d’onde de ce point sera toujours tangente à la position occupée par l’onde plane au bout de l’unité de temps ; par conséquent, elle est l’enveloppe de ces positions.

181. Direction du rayon lumineux. — Voici comment on peut, en s’appuyant sur le principe de Huyghens, déterminer la direction du rayon lumineux. Soit $\mathrm {P}$ (fig. 21) la position
Fig. 21. du plan de l’onde à un instant quelconque, et $\mathrm {P} '$ la nouvelle position du plan de l’onde au bout de l’unité de temps.

Supposons maintenant que le plan $\mathrm {P}$ ne soit pas tout entier ébranlé, et que la partie éclairée de ce plan se réduise à un élément $\mathrm {AB} ,$ ayant son centre de gravité en $\mathrm {O} ,$ très petit, d’une manière absolue, mais assez grand toutefois, pour qu’on puisse négliger les phénomènes de diffraction.

On obtiendra la portion éclairée du plan $\mathrm {P} '$ en construisant les surfaces de l’onde qui ont pour centres les divers points de $\mathrm {AB} ,$ et on cherchera les points de contact de ces surfaces avec le plan $\mathrm {P} '.$ Les points ainsi obtenus formeront un élément plan $\mathrm {A'B'}$ ayant son centre de gravité en $\mathrm {O} '.$ La droite $\mathrm {OO} '$ est alors le rayon lumineux cherché, d’où la règle suivante :

On obtiendra la direction du rayon lumineux en joignant le point $O$ au point de contact de la surface de l’onde, qui a son centre en $O,$ avec un plan tangent parallèle au plan de l’onde.

Nous allons appliquer cette règle sans nous inquiéter des objections soulevées par le principe de Huyghens. Nous en donnerons d’ailleurs plus loin (189) une démonstration rigoureuse.

182. Soient $\alpha ,\,\beta ,\,\gamma$ les cosinus directeurs de la normale à une onde plane, $\mathrm {V}$ la vitesse de propagation de cette onde, et $x,\,y,\,z$ les coordonnées du point où la surface d’onde est rencontrée par le rayon lumineux passant par l’origine. Ce point appartenant au plan occupé par l’onde au bout de l’unité de temps, ses coordonnées satisfont à l’équation

(1)

$\alpha x+\beta y+\gamma z=\mathrm {V} \,;$

comme il appartient également à l’enveloppe de ce plan on a aussi

(2)

$x\,d\alpha +y\,d\beta +z\,d\gamma =d\mathrm {V} .$

Quant à la vitesse de propagation $\mathrm {V} ,$ nous savons que dans toutes les. théories de la double réfraction que nous avons exposées, elle est donnée par l’équation

(3)

${\frac {\alpha ^{2}}{\mathrm {V} ^{2}-a}}+{\frac {\beta ^{2}}{\mathrm {V} ^{2}-b}}+{\frac {\gamma ^{2}}{\mathrm {V} ^{2}-c}}=\mathrm {F} (\alpha ,\,\beta ,\,\gamma ,\,\mathrm {V} )=0,$

qui, par différentiation, donne :

${\frac {d\mathrm {F} }{d\alpha }}\,d\alpha +{\frac {d\mathrm {F} }{d\beta }}\,d\beta +{\frac {d\mathrm {F} }{d\gamma }}\,d\gamma +{\frac {d\mathrm {F} }{d\mathrm {V} }}\,d\mathrm {V} =0.$

En y remplaçant $d\mathrm {V}$ par le premier membre de l’égalité (2) cette équation devient :

(4)

$\left({\frac {d\mathrm {F} }{d\alpha }}\!+\!x{\frac {d\mathrm {F} }{d\mathrm {V} }}\right)d\alpha +\left({\frac {d\mathrm {F} }{d\beta }}\!+\!y{\frac {d\mathrm {F} }{d\mathrm {V} }}\right)d\beta +\left({\frac {d\mathrm {F} }{d\gamma }}\!+\!z{\frac {d\mathrm {F} }{d\mathrm {V} }}\right)d\gamma =0.$

D’ailleurs $\alpha ,\,\beta ,\,\gamma$ sont liés par la relation

$\alpha ^{2}+\beta ^{2}+\gamma ^{2}=1,$

qui donne par différentiation

(5)

$\alpha \,d\alpha +\beta \,d\beta +\gamma \,d\gamma =0.$

Les deux relations (4) et (5), satisfaites à la fois pour toutes les valeurs que l’on peut donner à $d\alpha$ et $d\beta ,$ doivent être identiques ; nous aurons donc en introduisant une constante arbitraire $\mathrm {K}$

(6)

${\begin{aligned}{\frac {d\mathrm {F} }{d\alpha }}+x\,{\frac {d\mathrm {F} }{d\mathrm {V} }}&=\mathrm {K} \alpha ,\\[1.5ex]{\frac {d\mathrm {F} }{d\beta }}+y\,{\frac {d\mathrm {F} }{d\mathrm {V} }}&=\mathrm {K} \beta ,\\[1.5ex]{\frac {d\mathrm {F} }{d\gamma }}+z\,{\frac {d\mathrm {F} }{d\mathrm {V} }}&=\mathrm {K} \gamma .\\\end{aligned}}$

Cherchons les valeurs de $\mathrm {K}$ et des dérivées partielles qui entrent dans ces équations. Pour cela rappelons que la vitesse de propagation $\mathrm {V}$ satisfait aux équations

(I)

${\begin{aligned}\mathrm {AV} ^{2}&=a\mathrm {A} -\alpha \mathrm {H} ,\\[1.25ex]\mathrm {BV} ^{2}&=b\mathrm {B} -\beta \mathrm {H} ,\\[1.25ex]\mathrm {CV} ^{2}&=c\mathrm {C} -\gamma \mathrm {H} ,\\\end{aligned}}$

ou

$\mathrm {H} =\mathrm {A} a\alpha +\mathrm {B} b\beta +\mathrm {C} c\gamma ,$

et qui par élimination de $\mathrm {H}$ nous ont conduit (154) à l’équation (3). Nous aurons

${\frac {d\mathrm {F} }{d\alpha }}=-{\frac {2\alpha }{\mathrm {V} ^{2}-a}},$

et, en remplaçant $\mathrm {V} ^{2}-a$ par sa valeur tirée de la première des équations du groupe (I),

${\frac {d\mathrm {F} }{d\alpha }}=-{\frac {2\mathrm {A} }{\mathrm {H} }}\cdot$

Nous trouverons

${\frac {d\mathrm {F} }{d\beta }}=-{\frac {2\mathrm {B} }{\mathrm {H} }},\qquad \qquad {\frac {d\mathrm {F} }{d\gamma }}=-{\frac {2\mathrm {C} }{\mathrm {H} }},$

de la même manière.

Pour la dérivée par rapport à $\mathrm {V}$ nous aurons

${\begin{aligned}{\frac {d\mathrm {F} }{d\mathrm {V} }}=-\sum {\frac {2\alpha ^{2}\mathrm {V} }{\left(\mathrm {V} ^{2}-a\right)^{2}}}=-2\mathrm {V} &\sum {\frac {\alpha ^{2}}{\left(\mathrm {V} ^{2}-a\right)^{2}}}=\\&\qquad \qquad =-{\frac {2\mathrm {V} }{\mathrm {H} ^{2}}}\sum \mathrm {A} ^{2}.\\\end{aligned}}$

Or nous avons vu (155) que si le point $\mathrm {A,\,B,\,C}$ est sur l’ellipsoïde d’élasticité, on a

$\mathrm {V} ={\frac {1}{\sqrt {\mathrm {A} ^{2}+\mathrm {B} ^{2}+\mathrm {C} ^{2}}}}\,;$

il en résulte

${\frac {d\mathrm {F} }{d\mathrm {V} }}=-{\frac {2\mathrm {V} }{\mathrm {H} ^{2}}}{\frac {1}{\mathrm {V} ^{2}}}=-{\frac {2}{\mathrm {V} \mathrm {H} ^{2}}}\cdot$

Calculons le coefficient $\mathrm {K} .$ Pour cela multiplions les équations (6) par $\alpha ,\,\beta ,\,\gamma$ et additionnons, nous aurons

$\mathrm {K} =\sum \alpha \,{\frac {d\mathrm {F} }{d\alpha }}+{\frac {d\mathrm {F} }{d\mathrm {V} }}\sum \alpha x\,;$

mais

$\sum \alpha \,{\frac {d\mathrm {F} }{d\alpha }}=-\sum {\frac {2\mathrm {A} \alpha }{\mathrm {H} }}=0,$

et d’après l’équation (1)

$\sum \alpha x=\mathrm {V} .$

Par conséquent

$\mathrm {K} ={\frac {d\mathrm {F} }{d\mathrm {V} }}\mathrm {V} =-{\frac {2}{\mathrm {H} ^{2}}}\cdot$

En portant ces valeurs $\mathrm {K}$ et des dérivées partielles dans les équations (6), puis multipliant par $-{\frac {2}{\mathrm {H} ^{2}}},$ nous obtiendrons

(II)

${\begin{aligned}\mathrm {A} \mathrm {H} +{\frac {x}{\mathrm {V} }}=\alpha ,\\[1.5ex]\mathrm {B} \mathrm {H} +{\frac {y}{\mathrm {V} }}=\beta ,\\[1.5ex]\mathrm {C} \mathrm {H} +{\frac {z}{\mathrm {V} }}=\gamma ,\\[1.5ex]\end{aligned}}$

équations qui nous donneront les coordonnées $x,\,y,\,z$ du point d’intersection de la surface d’onde par le rayon lumineux.

183. Relations entre la direction du rayon lumineux et celles des vibrations. — Considérons la vibration de Neumann dont les cosinus directeurs sont proportionnels à $\mathrm {A',\,B',\,C'} .$ Si nous multiplions les équations du groupe (II) par $\mathrm {A',\,B',\,C'}$ nous obtenons pour la somme de ces produits

$\mathrm {H} \sum \mathrm {AA} '+{\frac {1}{\mathrm {V} }}\sum \mathrm {A} 'x=\sum \mathrm {A} '\alpha \cdot$

Nous savons d’ailleurs que la vibration de Neumann est située dans le plan de l’onde et qu’elle est perpendiculaire à celle de Fresnel ; par conséquent, nous aurons

${\begin{aligned}\mathrm {A} '\,\alpha +\mathrm {B} '\,\beta +\mathrm {C} '\,\gamma &=0,\\\mathrm {AA} '+\mathrm {BB} '+\mathrm {CC} '&=0,\\\end{aligned}}$

et la relation précédente se réduira à la suivante

$\mathrm {A} 'x+\mathrm {B} 'y+\mathrm {C} 'z=0$

qui exprime que la vibration de Neumann est perpendiculaire au rayon lumineux.

Prenons maintenant la vibration de M. Sarrau, dont les cosinus directeurs sont proportionnels à $\mathrm {A} a,$ $\mathrm {B} b,$ $\mathrm {C} c.$ En multipliant respectivement chacune des équations (II) par ces quantités et additionnant, nous avons

$\mathrm {H} \sum a\mathrm {A} ^{2}+{\frac {1}{\mathrm {V} }}\sum a\mathrm {A} x=\sum \mathrm {A} a\alpha .$

Le point de coordonnées $\mathrm {A,\,B,\,C}$ étant sur l’ellipsoïde d’élasticité, $\textstyle \sum a\mathrm {A} ^{2}=1\,;$ d’autre part, par hypothèse, $\textstyle \mathrm {H} =\sum \mathrm {A} a\alpha .$ Par conséquent, la relation précédente se réduit à la suivante

$a\mathrm {A} x+b\mathrm {B} y+c\mathrm {C} z=0,$

qui exprime que la vibration de M. Sarrau est perpendiculaire au rayon lumineux.

184. Équation de la surface d’onde. — L’équation de cette surface s’obtiendra en éliminant $\alpha ,\,\beta ,\,\gamma ,$ $\mathrm {A,\,B,\,C}$ et $\mathrm {V}$ entre les équations formant les groupes (I) et (II) et la suivante

(IV)

$\mathrm {A} ax+\mathrm {B} by+\mathrm {C} cz=0,$

que nous venons de déduire du groupe (II).

La première des équations (II) peut s’écrire

${\frac {x\mathrm {H} }{\mathrm {V} }}=\alpha \mathrm {H} -\mathrm {A} \mathrm {H} ^{2},$

et la première des équations (I) nous donne

$\alpha \mathrm {H} =\mathrm {A} \left(a-\mathrm {V} ^{2}\right),$

Nous aurons donc

${\frac {x\mathrm {H} }{\mathrm {V} }}=\mathrm {A} \left(a-\mathrm {V} ^{2}-\mathrm {H} ^{2}\right).$

Cherchons la valeur de $\mathrm {V} ^{2}+\mathrm {H} ^{2}.$ Pour cela tirons des équations (II) les valeurs de $x,\,y,\,z$ et formons les carrés de ces quantités ; nous aurons :

${\begin{alignedat}{3}x&=\alpha \mathrm {V} -\mathrm {A} \mathrm {H} \mathrm {V} ,&\qquad x^{2}&=\alpha ^{2}\mathrm {V} ^{2}-2\mathrm {A} \alpha \mathrm {H} \mathrm {V} ^{2}+\mathrm {A} ^{2}\mathrm {H} ^{2}\mathrm {V} ^{2},\\y&=\beta \mathrm {V} -\mathrm {B} \mathrm {H} \mathrm {V} ,&\qquad y^{2}&=\beta ^{2}\mathrm {V} ^{2}-2\mathrm {B} \beta \mathrm {H} \mathrm {V} ^{2}\,+\mathrm {B} ^{2}\mathrm {H} ^{2}\mathrm {V} ^{2},\\z&=\gamma \mathrm {V} -\mathrm {C} \mathrm {H} \mathrm {V} ,&\qquad z^{2}&=\gamma ^{2}\mathrm {V} ^{2}-2\mathrm {C} \gamma \mathrm {H} \mathrm {V} ^{2}\,+\mathrm {C} ^{2}\mathrm {H} ^{2}\mathrm {V} ^{2},\\\end{alignedat}}$

et par conséquent

$x^{2}+y^{2}+z^{2}=r^{2}=\mathrm {V} ^{2}-2\mathrm {H} \mathrm {V} ^{2}\sum \mathrm {A} \alpha +\mathrm {H} ^{2}\mathrm {V} ^{2}\sum \mathrm {A} ^{2}.$

Nous avons déjà vu que $\textstyle \sum \mathrm {A} \alpha =0$ et $\textstyle \sum \mathrm {A} ^{2}={\dfrac {1}{\mathrm {V} ^{2}}}\,;$ par suite nous aurons pour le carré du rayon vecteur de la surface d’onde

$r^{2}=\mathrm {V} ^{2}+\mathrm {H} ^{2}.$

En portant cette valeur de $\mathrm {V} ^{2}+\mathrm {H} ^{2}$ dans l’expression précédemment obtenue de ${\frac {x\mathrm {H} }{\mathrm {V} }},$ nous obtiendrons

${\frac {x\mathrm {H} }{\mathrm {V} }}=\mathrm {A} (a-r^{2}),$

ou

${\frac {x}{r^{2}-a}}=-{\frac {\mathrm {AV} }{\mathrm {H} }},$

et par symétrie,

${\begin{aligned}{\frac {y}{r^{2}-b}}&=-{\frac {\mathrm {BV} }{\mathrm {H} }},\\[1.5ex]{\frac {z}{r^{2}-c}}&=-{\frac {\mathrm {CV} }{\mathrm {H} }}\cdot \\\end{aligned}}$

Nous avons ainsi des quantités proportionnelles à $\mathrm {A,\,B,\,C}$ qui portées à la place de $\mathrm {A,\,B,\,C}$ dans l’équation (IV) nous donneront

${\frac {ax^{2}}{r^{2}-a}}+{\frac {by^{2}}{r^{2}-b}}+{\frac {cz^{2}}{r^{2}-c}}=0\,;$

c’est l’équation de la surface d’onde sous sa forme la plus simple.

Cette surface paraît être du sixième degré ; il est facile de montrer par le développement de l’équation précédente qu’elle est seulement du quatrième degré. On aura en chassant les dénominateurs

$\sum ax^{2}(r^{2}-b)(r^{2}-c)=0,$

ou

$r^{4}\sum ax^{2}-r^{2}\sum (b+c)ax^{2}+abc(x^{2}+y^{2}+z^{2})=0.$

$r^{2}$ se trouve donc en facteur ; en supprimant ce facteur on obtient

$\sum x^{2}\sum ax^{2}-\sum (ab+ac)x^{2}+abc=0,$

équation qui n’est que du quatrième degré.

185. Construction géométrique de la surface d’onde. — Considérons une onde plane et prenons pour plan de figure un plan perpendiculaire au plan d’onde et passant par la vibration
Fig. 22. de Fresnel. Cette vibration sera représentée par la droite $\mathrm {OF}$ (fig. 22). La vibration de Neumann, située dans le plan de l’onde et perpendiculaire à celle de Fresnel, sera normale au plan de la figure et se projettera au point $\mathrm {O} .$ Le rayon lumineux et la vibration de M. Sarrau tous deux perpendiculaires à la vibration de Neumann, seront situés dans le plan du tableau ; soient $\mathrm {OS} ,$ la vibration de M. Sarrau, $\mathrm {OM} ,$ le rayon lumineux, droites qui sont rectangulaires entre elles. La position du plan de l’onde au bout de l’unité de temps est représentée par sa trace $\mathrm {PM} .$

Le plan tangent à l’ellipsoïde d’élasticité

$ax^{2}+by^{2}+cz^{2}=1$

au point $\mathrm {F}$ de coordonnées $\mathrm {A,\,B,\,C}$ a pour équation

$a\mathrm {A} x+b\mathrm {B} y+c\mathrm {C} z=1.$

Les cosinus directeurs de la normale à ce plan sont proportionnels à $a\mathrm {A} ,$ $b\mathrm {B} ,$ $c\mathrm {C} ,$ c’est-à-dire aux composantes de la vibration de M. Sarrau. Ce plan tangent sera donc perpendiculaire au plan de la figure sur laquelle il se trouvera représenté par la perpendiculaire $\mathrm {FQ}$ sur $\mathrm {OS} .$ — Ce résultat peut être obtenu d’une autre manière. La droite $\mathrm {OF}$ est un axe de l’ellipse d’intersection $\mathrm {E}$ de l’ellipsoïde d’élasticité par le plan de l’onde ; par conséquent, la tangente en $\mathrm {F}$ à cette ellipse est perpendiculaire à $\mathrm {OF} ,$ et, comme en outre elle est située dans le plan de l’onde, perpendiculaire au plan de la figure, elle est elle-même perpendiculaire à ce dernier plan. Le plan tangent à l’ellipsoïde en $\mathrm {F}$ contenant cette tangente sera aussi perpendiculaire au plan de la figure.

Considérons la sphère décrite du point $\mathrm {O}$ comme centre avec un rayon égal à l’unité. Si nous prenons sur la droite $\mathrm {OQ}$ une longueur $\mathrm {OS} ={\frac {1}{\mathrm {OQ} }}$ le point $\mathrm {S}$ est le pôle du plan $\mathrm {FQ}$ par rapport à cette sphère. Par conséquent, le lieu du point $\mathrm {S}$ quand le point $\mathrm {F}$ décrit l’ellipsoïde d’élasticité sera l’ellipsoïde polaire réciproque de l’ellipsoïde d’élasticité. Cet ellipsoïde réciproque a donc pour équation

${\frac {x^{2}}{a}}+{\frac {y^{2}}{b}}+{\frac {z^{2}}{c}}=1.$

Menons le plan tangent en $\mathrm {S}$ à cet ellipsoïde ; il a pour pôle le point $\mathrm {F} \,;$ par conséquent, il est perpendiculaire au rayon $\mathrm {OF} ,$ et il coupe le plan de la figure suivant $\mathrm {ST} .$ Nous allons en déduire que la droite $\mathrm {OS}$ est un axe de l’ellipse d’intersection $\mathrm {E} '$ de l’ellipsoïde réciproque $\mathrm {S}$ par un plan perpendiculaire au rayon lumineux. En effet, la tangente en $\mathrm {S}$ à cette ellipse est située dans le plan de section et dans le plan tangent à l’ellipsoïde ; ces deux plans étant perpendiculaires au plan de la figure, la tangente est aussi perpendiculaire à ce dernier plan, et, par suite, au rayon vecteur OS qui doit alors être un axe.

Montrons maintenant que l’on a $\mathrm {OM} =\mathrm {OS} .$ Les droites $\mathrm {OM}$ et $\mathrm {OP}$ étant respectivement perpendiculaires à $\mathrm {OS}$ et $\mathrm {OF} ,$ les angles $\mathrm {FOS}$ et $\mathrm {POM}$ sont égaux. Nous aurons donc, puisque $\mathrm {OP} ,$ vitesse de propagation normale d’une onde plane, est égal à l’inverse de l’axe $\mathrm {OF}$ de l’ellipse $\mathrm {E} ,$

$\mathrm {OM} ={\frac {\mathrm {OP} }{\cos \theta }}={\frac {1}{\mathrm {OF} \,\cos \theta }}\cdot$

D’autre part le triangle $\mathrm {OFQ}$ nous donne

$\mathrm {OS} ={\frac {1}{\mathrm {OQ} }}={\frac {1}{\mathrm {OF} \,\cos \theta }}\cdot$

Nous avons donc bien $\mathrm {OM} =\mathrm {OS} .$

Le point $\mathrm {M}$ étant un point de la surface d’onde, nous pourrons construire cette surface de la manière suivante : Couper l’ellipsoïde réciproque $\mathrm {S}$ par un plan quelconque, et porter sur la normale $\mathrm {OM}$ à ce plan des longueurs égales aux axes de l’ellipse $\mathrm {E} '$ d’intersection.

186. Sections de la surface d’onde par les plans de symétrie. — Prenons pour plans de figure l’un des trois plans de symétrie optique du milieu. Ces plans étant les plans principaux de l’ellipsoïde d’élasticité seront également les plans principaux de l’ellipsoïde réciproque $\mathrm {S} .$ Un plan
Fig. 23. perpendiculaire au plan de la figure et passant par le centre de cet ellipsoïde contiendra donc un de ses axes, celui qui est perpendiculaire au plan de figure. Si $\mathrm {OS}$ (fig. 23) est le plan de section considéré, on aura les deux points correspondants de la surface d’onde en portant sur la normale $\mathrm {OM}$ à ce plan la longueur $\mathrm {OM} =\mathrm {OS}$ et la longueur $\mathrm {OM} '$ égale à l’axe projeté en $\mathrm {O} .$ Les deux points $\mathrm {M}$ et $\mathrm {M} '$ sont situés dans le plan de la figure, et on obtiendra l’intersection de la surface d’onde par ce plan en faisant tourner le plan $\mathrm {OS}$ autour de la normale passant par $\mathrm {O} .$ L’un des axes des sections ainsi obtenues étant
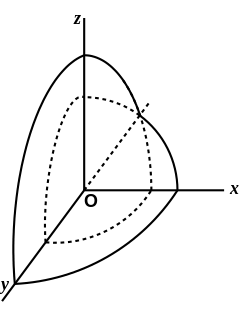
Fig. 24. l’axe projeté en $\mathrm {O} ,$ la longueur $\mathrm {OM} '$ sera constante et le point $\mathrm {M} '$ décrira un cercle. Le point $\mathrm {M}$ décrira une ellipse qui n’est autre que l’ellipse $\mathrm {AB}$ d’intersection de l’ellipsoïde réciproque par le plan de la figure, ellipse dont on a fait tourner les axes de 90°.

L’intersection de la surface d’onde par chacun des plans de symétrie se compose donc d’un cercle et d’une ellipse. La connaissance de ces intersections permet de se rendre assez bien compte de la forme de la surface d’onde. Si nous supposons que l’on ait $a>b>c$ la partie de la surface d’onde comprise dans le trièdre où les trois coordonnées d’un point sont positives aura la forme représentée par la figure 23.

Dans le cas particulier de cristaux à un axe l’ellipsoïde d’élasticité est de révolution ; l’ellipsoïde réciproque, et par suite la surface d’onde le sont également. L’intersection de cette surface par deux des plans de symétrie se compose d’une ellipse et d’un cercle ; l’intersection par le troisième plan de symétrie est formée de deux cercles. — La surface d’onde se compose alors d’une sphère et d’un ellipsoïde de révolution tangents.

187. Ombilics et plans tangents singuliers de la surface d’onde. — Considérons un plan cyclique de l’ellipsoïde réciproque. Tous les rayons vecteurs de cette section seront des axes égaux ; par conséquent, à un plan cyclique ne correspond qu’un seul point $\mathrm {M}$ de la surface d’onde. Mais, à chaque direction $\mathrm {OS}$ d’un axe correspond un plan tangent normal au plan passant par $\mathrm {OS}$ et $\mathrm {OM} \,;$ nous aurons donc une infinité de plans tangents en $\mathrm {M} .$ C’est un point conique. Comme à chaque section cyclique correspondent deux points coniques, nous aurons quatre points coniques réels et huit points coniques imaginaires. On appelle encore ces points les ombilics de la surface d’onde.

Le cône formé par les plans tangents à la surface d’onde en un point conique est du second degré. En effet, il ne peut être du troisième degré, car la droite passant par deux de ces points rencontrerait la surface en six points, ce qui ne peut avoir lieu puisque cette surface est du quatrième degré.

La considération des plans cycliques de l’ellipsoïde d’élasticité conduit à une nouvelle propriété intéressante de la surface d’onde.

Si nous supposons que le plan de l’onde soit un plan cyclique, tout rayon du cercle d’intersection sera une direction de la vibration de Fresnel. À chacune de ces directions correspond un plan tangent $\mathrm {PM}$ à la surface d’onde ; mais comme $\mathrm {OP} ={\frac {1}{\mathrm {OF} }}$ et que $\mathrm {OF}$ est constant, ces divers plans tangents se confondent. Leurs points de contact avec la surface d’onde ne se confondent cependant pas, car à chaque direction de $\mathrm {OF}$ correspond une direction particulière de $\mathrm {OS}$ et, par suite, de $\mathrm {OM} .$ Par conséquent, le plan $\mathrm {PM}$ correspondant à une section circulaire de l’ellipsoïde touche la surface d’onde en une infinité de points distincts. Ces points forment une courbe qui doit être du second degré, car, en général, la section d’une surface par un plan tangent singulier se composant de deux courbes confondues, chacune de ces courbes est d’un degré égal à la moitié du degré de la surface. D’ailleurs, cette courbe du second degré est un cercle. En effet, les directions asymptotiques de la surface sont données par les termes du plus haut degré $\textstyle \sum x^{2}\sum ax^{2}\,;$ deux de ces directions sont celles d’un cercle, et comme pour les plans tangents singuliers les directions asymptotiques doivent se confondre deux à deux, puisque les courbes d’intersection se confondent, les quatre directions asymptotiques sont celles de cercles. La courbe d’intersection de la surface par un plan tangent singulier se compose donc de deux cercles confondus. Il y aura quatre de ces plans tangents singuliers qui seront réels, un ellipsoïde ayant deux directions de sections cycliques à chacune desquelles correspondent deux plans tangents singuliers.

Bien d’autres propriétés de la surface d’onde ont été étudiées par divers mathématiciens. En particulier, nous citerons les procédés élégants indiqués par M. Mannheim pour trouver les rayons de courbure et tracer les lignes de courbure de la surface d’onde. Mais nous n’insisterons pas sur ces propriétés qui n’ont aucun intérêt au point de vue de l’Optique. Seule, la considération des ombilics et des plans tangents singuliers a une grande importance. On sait, en effet, qu’elle a conduit Hamilton à la découverte de la réfraction conique intérieure et de la réfraction conique extérieure que Lloyd a pu mettre en évidence par des expériences délicates.

PROPAGATION RECTILIGNE DE LA LUMIÈRE.

188. Propagation rectiligne de la lumière dans un milieu isotrope. — Nous avons déterminé plus haut (181) la direction du rayon lumineux dans un milieu cristallisé en nous appuyant sur le principe de Huyghens ; mais ce principe, quelles que soient l’utilité et l’importance de son rôle en optique, prête à un grand nombre d’objections dont nous avons cherché à donner une idée dans la première partie du cours.

Aussi ne sera-t-il pas inutile d’expliquer ici comment on peut déterminer la direction du rayon lumineux dans un milieu isotrope ou anisotrope en s’affranchissant du principe de Huyghens et des difficultés sans nombre qu’il soulève. Nous commencerons par le cas le plus simple qui est celui des milieux isotropes, et nous écrirons les équations du mouvement transversal sous la forme habituelle,

${\begin{aligned}\rho \,{\frac {d^{2}\xi }{dt^{2}}}&=\Delta \xi ,\\[1.5ex]\rho \,{\frac {d^{2}\eta }{dt^{2}}}&=\Delta \eta ,\\[1.5ex]\rho \,{\frac {d^{2}\zeta }{dt^{2}}}&=\Delta \zeta ,\\\end{aligned}}$

avec

$\Theta =0.$

Cherchons à satisfaire à ces équations en faisant :

(1)

${\begin{aligned}\xi &=\mathrm {A} e^{\mathrm {P} },&\eta &=\mathrm {B} e^{\mathrm {P} },&\zeta &=\mathrm {C} e^{\mathrm {P} },\end{aligned}}$

où

$\mathrm {P} =2i\pi \left({\frac {z-\mathrm {V} t}{\lambda }}\right)\cdot$

Si nous regardions $\mathrm {A,\,B,\,C}$ comme des constantes, nous retomberions sur la théorie ordinaire de la propagation d’une onde plane indéfinie. Mais alors la question de la direction du rayon lumineux ne se poserait pas, puisque tout l’espace se trouverait également éclairé. Nous devons donc supposer qu’une portion seulement de l’éther est agitée par des ondulations et par conséquent que $\mathrm {A,\,B,\,C}$ sont des fonctions de $x,\,y,\,z$ et $t.$

Nous prendrons une unité de longueur comparable à nos unités habituelles, de telle sorte que $\lambda$ sera une longueur très petite et ${\frac {2i\pi }{\lambda }}$ une quantité infiniment grande ; (si dans l’exposition de la théorie de M. Sarrau, nous avons regardé cette quantité comme très petite c’est que nous avions pris une unité de longueur comparable à la distance qui sépare deux molécules matérielles). Au contraire nous supposerons que les fonctions $\mathrm {A,\,B,\,C}$ et leurs dérivées des divers ordres sont finies.

Les considérations qui vont suivre ne s’appliquent donc pas, du moins sans modification, au cas où les fonctions $\mathrm {A,\,B,\,C}$ sont discontinues et où par conséquent leurs dérivées ne sont pas finies ; dans ce cas, en effet, il se produit des phénomènes de diffraction et il y a déviation du rayon lumineux.

Substituons les valeurs (1) dans la première des équations du mouvement, il viendra, en divisant par $-e^{\mathrm {P} }{\frac {4\pi ^{2}}{\lambda ^{2}}},$

$\rho \left(\mathrm {V^{2}A} -{\frac {\lambda }{i\pi }}\,\mathrm {V} \,{\frac {d\mathrm {A} }{dt}}-{\frac {\lambda ^{2}}{4\pi ^{2}}}{\frac {d^{2}\mathrm {A} }{dt^{2}}}\right)=\mathrm {A} +{\frac {\lambda }{i\pi }}{\frac {d\mathrm {A} }{dz}}-{\frac {\lambda ^{2}}{4\pi ^{2}}}\,\Delta \mathrm {A}$

Nous négligerons les termes en $\lambda ^{2}\,;$ si nous remarquons que $\rho \mathrm {V} ^{2}=1,$ nous verrons que les termes indépendants de $\lambda$ disparaissent ; les deux membres contiendront alors le facteur ${\frac {\lambda }{i\pi }}\cdot$ Si nous faisons disparaître ce facteur, il restera simplement

(2)

${\frac {d\mathrm {A} }{dt}}+\mathrm {V} \,{\frac {d\mathrm {A} }{dz}}=0.$

On trouverait de même

${\frac {d\mathrm {B} }{dt}}+\mathrm {V} \,{\frac {d\mathrm {B} }{dz}}=0\qquad \quad {\frac {d\mathrm {C} }{dt}}+\mathrm {V} \,{\frac {d\mathrm {C} }{dz}}=0$

Si nous substituons les valeurs (1) dans l’équation $\Theta =0$ et que nous la divisions par $e^{\mathrm {P} },$ il viendra

${\frac {2i\pi }{\lambda }}\mathrm {C} +{\frac {d\mathrm {A} }{dx}}+{\frac {d\mathrm {B} }{dy}}+{\frac {d\mathrm {C} }{dz}}=0.$

Cette équation nous montre que $\mathrm {C}$ est un infiniment petit du même ordre que $\lambda .$ Quant à l’équation (2), elle a pour intégrale générale :

$\mathrm {A} =$ fonction arbitraire de $x,\,y$ et $z-\mathrm {V} t.$

Ainsi la valeur de $\mathrm {A}$ au temps $t$ et au point dont les coordonnées sont $x,\,y,$ et $z+\mathrm {V} t,$ sera la même qu’au temps $0$ et au point $x,\,y,\,z.$ Si à l’origine des temps il n’y a de lumière sensible qu’à l’intérieur d’une petite sphère ayant pour centre le point $x,\,y,\,z\,;$ à l’époque $t,$ il n’y aura de lumière sensible qu’à l’intérieur d’une petite sphère du même rayon ayant pour centre le point $x,\,y$ et $z+\mathrm {V} t.$ En d’autres termes, la lumière se sera propagée dans la direction de l’axe des $z,$ c’est-à-dire perpendiculairement au plan de l’onde.

Ainsi dans un milieu isotrope le rayon lumineux est normal au plan de l’onde.

189. Propagation rectiligne de la lumière dans un milieu anisotrope. — Passons au cas d’un milieu cristallisé, et prenons par exemple les équations de M. Sarrau :

(1)

${\begin{aligned}{\frac {1}{a}}{\frac {d^{2}\xi }{dt^{2}}}=&\Delta \xi -{\frac {d\Theta }{dx}},\\[1.5ex]{\frac {1}{b}}{\frac {d^{2}\eta }{dt^{2}}}=&\Delta \eta -{\frac {d\Theta }{dy}},\\[1.5ex]{\frac {1}{c}}{\frac {d^{2}\zeta }{dt^{2}}}=&\Delta \zeta -{\frac {d\Theta }{dz}}\cdot \\\end{aligned}}$

Cherchons à y satisfaire en posant

${\begin{array}{c}\xi =\mathrm {L} e^{\mathrm {P} },\qquad \quad \eta =\mathrm {M} e^{\mathrm {P} },\qquad \quad \zeta =\mathrm {N} e^{\mathrm {P} },\\[1.25ex]\mathrm {P} ={\dfrac {2i\pi }{\lambda }}\left(\alpha x+\beta y+\gamma z-\mathrm {V} t\right),\\\end{array}}$

$\mathrm {L,\,M,\,N}$ étant des fonctions de $x,\,y,\,z$ et $t.$

Si $\mathrm {L,\,M}$ et $\mathrm {N}$ devaient être des constantes $\mathrm {L_{0},\,M_{0},\,N_{0}} ,$ ces constantes et $\mathrm {V}$ devraient satisfaire aux équations

(2)

${\begin{array}{c}\;\;{\dfrac {\mathrm {V} ^{2}\mathrm {L} _{0}}{a}}=\mathrm {L} _{0}-\alpha \mathrm {H} ,\quad {\dfrac {\mathrm {V} ^{2}\mathrm {M} _{0}}{b}}=\mathrm {M} _{0}-\beta \mathrm {H} ,\quad {\dfrac {\mathrm {V} ^{2}\mathrm {N} _{0}}{c}}=\mathrm {N} _{0}-\gamma \mathrm {H} .\\[1ex]\mathrm {H} =\alpha \mathrm {L} _{0}+\beta \mathrm {M} _{0}+\gamma \mathrm {N} _{0}.\\\end{array}}$

Posons alors :

${\begin{aligned}\mathrm {L} &=\mathrm {L} _{0}f+g,&\mathrm {M} &=\mathrm {M} _{0}f+h,&\mathrm {N} &=\mathrm {N} _{0}f,\end{aligned}}$

et cherchons à déterminer les trois fonctions $f,g$ et $h$.

Pour obtenir ces trois fonctions, substituons dans les équations du mouvement à la place de $\xi ,\,\eta ,\,\zeta ,$ leurs valeurs, c’est-à-dire,

${\begin{aligned}\xi &=(\mathrm {L} _{0}f+g)e^{\mathrm {P} },&\eta &=(\mathrm {M} _{0}f+h)e^{\mathrm {P} },&\zeta &=\mathrm {N} _{0}fe^{\mathrm {P} }.\end{aligned}}$

Nous obtiendrons ainsi trois équations différentielles entre $f,$ $g$ et $h.$ D’après leur mode de formation ces équations seront :

1^o Linéaires et homogènes par rapport à $f,$ $g$ et $h$ et à leurs dérivées partielles des deux premiers ordres ;

2^o À coefficients constants, après que l’on aura supprimé le facteur commun $e^{\mathrm {P} }.$

Éliminons maintenant $g$ et $h$ entre ces trois équations ; il restera une équation différentielle unique qui définira $f.$

Cette équation sera encore linéaire, homogène et à coefficients constants ; mais elle sera d’ordre supérieur au second.

Elle ne contiendra pas $f\,;$ car les équations du mouvement doivent être satisfaites quand on fait

$f=1,\qquad g=h=0.$

Elle ne changera pas quand on multipliera à la fois $\lambda ,\,x,\,y,\,z$ et $t$ par un même facteur, ce qui revient à changer simultanément et dans un même rapport l’unité de longueur et celle de temps.

Soit :

$\mathrm {A} \lambda ^{P}\mathrm {D} ^{m}f$

un terme quelconque du premier membre de notre équation ; $\mathrm {A}$ est une constante indépendante de $\lambda$ et $\mathrm {D} ^{m}f$ une des dérivées partielles d’ordre $m$ de $f.$ Quand on changera $\lambda ,\,x,\,y,\,z$ et $t$ en $k\lambda ,\,kx,\,ky,\,kz,$ et $kt,$ ce terme se trouvera multiplié par $k^{p-m}.$ Pour que l’équation ne change pas, il faut que $m-p$ ait même valeur pour tous les termes de l’équation. Nous multiplierons notre équation par une puissance de $\lambda$ telle que $m-p$ soit égal à $1.$

Alors les coefficients des dérivées du premier ordre ne contiendront pas $\lambda \,;$ ceux des dérivées du second ordre contiendront le facteur $\lambda \,;$ ceux des dérivées du troisième ordre contiendront le facteur $\lambda ^{2}\,;$ et ainsi de suite. Mais $\lambda$ étant très petit, nous pouvons négliger les termes qui contiennent ce facteur ; il ne nous restera plus alors que les dérivées du premier ordre et l’équation en $f$ s’écrira

$\mu \,{\frac {df}{dx}}+\mu '{\frac {df}{dy}}+\mu ''{\frac {df}{dz}}+{\frac {df}{dt}}=0$

$\mu ,\,\mu ',\,\mu ''$ étant des constantes.

L’intégrale générale de cette équation sera :

$f=$ fonction arbitraire de $x-\mu t,\,y-\mu 't,$ et $z-\mu ''t,$

ce qui veut dire que les cosinus directeurs du rayon lumineux sont proportionnels à $\mu ,\,\mu '$ et $\mu ''$ et que la vitesse de propagation, estimée non pas normalement au plan de l’onde, mais dans la direction du rayon est ${\sqrt {\mu ^{2}+\mu '^{2}+\mu ''^{2}}}.$

On pourrait déterminer $\mu \,\mu '$ et $\mu ''$ en effectuant tous les calculs que nous venons d’indiquer ; mais cela est inutile. En effet les équations du mouvement devront être satisfaites si l’on fait $f=e^{x-\mu t},$ d’où $g$ et $h=$ constante très petite $\times e^{x-\mu t}$ et

${\begin{aligned}\mathrm {L} &=\mathrm {L} '_{0}e^{x-\mu t},&\mathrm {M} &=\mathrm {M} '_{0}e^{x-\mu t},&\mathrm {N} &=\mathrm {N} '_{0}e^{x-\mu t}.\end{aligned}}$

$\mathrm {L'_{0},\,M'_{0}}$ et $\mathrm {N} _{0}'$ étant des constantes très peu différentes de $\mathrm {L_{0},\,M_{0}}$ et $\mathrm {N_{0}} .$ On aura alors

${\begin{array}{c}\xi =\mathrm {L} _{0}'e^{\mathrm {P} '},\qquad \eta =\mathrm {M} _{0}'e^{\mathrm {P} '},\qquad \zeta =\mathrm {N} _{0}'e^{\mathrm {P} '}\,;\\[1.25ex]\mathrm {P} '={\dfrac {2i\pi }{\lambda }}\left[\left(\alpha +{\dfrac {\lambda }{2i\pi }}\right)x+\beta y+\gamma z-\left(\mathrm {V} +{\dfrac {\lambda \mu }{2i\pi }}\right)t\right]\cdot \\\end{array}}$

Or nous avons vu que si $\xi ,\,\eta ,\,\zeta$ sont égaux à des constantes multipliées par $e^{\mathrm {P} }$ et que l’on pose :

$\mathrm {P} ={\dfrac {2i\pi }{\lambda }}\left(\alpha x+\beta y+\gamma z-\mathrm {V} t\right)$

$\lambda$ étant choisi de telle façon que $\alpha ^{2}+\beta ^{2}+\gamma ^{2}=1\,;$ on devra avoir

${\frac {\alpha ^{2}}{\mathrm {V} ^{2}-a}}+{\frac {\beta ^{2}}{\mathrm {V} ^{2}-b}}+{\frac {\gamma ^{2}}{\mathrm {V} ^{2}-c}}=0.$

Nous désignerons comme nous l’avons déjà fait plus haut le premier membre de cette équation par

$\mathrm {F} (\alpha ,\,\beta ,\,\gamma ,\,\mathrm {V} ).$

Comme $\alpha ^{2}+\beta ^{2}+\gamma ^{2}=1\,;$ nous aurons également

(3)

$\mathrm {F} \left(\alpha ,\,\beta ,\,\gamma ,\,{\frac {\mathrm {V} }{\sqrt {\alpha ^{2}+\beta ^{2}+\gamma ^{2}}}}\right)=0.$

La relation (3) étant homogène en $\alpha ,\,\beta ,\,\gamma$ et $\mathrm {V}$ subsistera

encore quand on aura multiplié à la fois $\alpha ,\,\beta ,\,\gamma$ et $\mathrm {V}$ par un

même facteur. Elle est donc encore vraie, même quand on ne

suppose plus que la somme $\alpha ^{2}+\beta ^{2}+\gamma ^{2}$ soit égale à 1.

Ainsi la relation (3) devra être satisfaite quand on y remplacera $\alpha ,\,\beta ,\,\gamma$ et $\mathrm {V}$ par les coefficients de $x,\,y,\,z$ et $-t$ dans $\mathrm {P} ',$ c’est-à-dire par

$\alpha +{\frac {\lambda }{2i\pi }},\qquad \beta ,\qquad \gamma \qquad \mathrm {et} \qquad \mathrm {V} +{\frac {\lambda \mu }{2i\pi }}\cdot$

On aura donc

(4)

$\mathrm {F} \left(\alpha +{\frac {\lambda }{2i\pi }},\,\beta ,\,\gamma ,\,{\frac {\mathrm {V} +{\dfrac {\lambda \mu }{2i\pi }}}{\sqrt {\left(\alpha +{\dfrac {\lambda }{2i\pi }}\right)^{2}+\beta ^{2}+\gamma ^{2}}}}\right)=0.$

Cela est vrai avec le degré d’approximation adopté plus haut, c’est-à-dire en supposant que $\lambda$ est très petit ; on a alors en négligeant $\lambda ^{2}$

${\begin{aligned}\left[\left(\alpha +{\dfrac {\lambda }{2i\pi }}\right)^{2}+\beta ^{2}+\gamma ^{2}\right]^{-{\frac {1}{2}}}&=\left[\left(\alpha ^{2}+\beta ^{2}+\gamma ^{2}\right)+{\frac {\alpha \lambda }{i\pi }}\right]^{-{\frac {1}{2}}}=\\[1.5ex]&\qquad \qquad =\left(1+{\frac {\alpha \lambda }{i\pi }}\right)^{-{\frac {1}{2}}}=1+{\frac {\alpha \lambda }{2i\pi }},\\\end{aligned}}$

et

${\frac {\mathrm {V} +{\dfrac {\lambda \mu }{2i\pi }}}{\sqrt {\left(\alpha +{\dfrac {\lambda }{2i\pi }}\right)^{2}+\beta ^{2}+\gamma ^{2}}}}=\mathrm {V} +{\frac {\lambda \mu }{2i\pi }}-{\frac {\alpha \mathrm {V} \lambda }{2i\pi }},$

${\begin{aligned}\mathrm {F} \left(\alpha +{\frac {\lambda }{2i\pi }},\,\beta ,\,\gamma ,{\frac {\mathrm {V} +{\dfrac {\lambda \mu }{2i\pi }}}{\sqrt {\left(\alpha +{\dfrac {\lambda }{2i\pi }}\right)^{2}+\beta ^{2}+\gamma ^{2}}}}\right)=\qquad \qquad \qquad &\\=\mathrm {F} (\alpha ,\,\beta ,\,\gamma ,\,\mathrm {V} )+{\dfrac {\lambda }{2i\pi }}\left[{\frac {d\mathrm {F} }{d\alpha }}+{\frac {d\mathrm {F} }{d\mathrm {V} }}(\mu -\alpha \mathrm {V} )\right]&\cdot \\\end{aligned}}$

Il reste donc en tenant compte des relations (3) et (4) :

${\begin{aligned}{\frac {d\mathrm {F} }{d\alpha }}+\;\mu \,{\frac {d\mathrm {F} }{d\mathrm {V} }}&=\alpha \mathrm {V} \,{\frac {d\mathrm {F} }{d\mathrm {V} }},\\[1.5ex]{\frac {d\mathrm {F} }{d\beta }}+\,\mu '{\frac {d\mathrm {F} }{d\mathrm {V} }}&=\beta \mathrm {V} \,{\frac {d\mathrm {F} }{d\mathrm {V} }},\\[1.5ex]{\frac {d\mathrm {F} }{d\gamma }}+\mu ''{\frac {d\mathrm {F} }{d\mathrm {V} }}&=\gamma \mathrm {V} \,{\frac {d\mathrm {F} }{d\mathrm {V} }}\cdot \\\end{aligned}}$

Si l’on compare ces équations aux équations (6) et du § (182), on verra que le point dont les coordonnées sont $\mu ,\,\mu '$ et $\mu ''$ n’est autre que le point que nous avons appelé $\mathrm {O} '$ dans ce paragraphe (voir figure 21) et dont les coordonnées étaient désignées par $x,\,y$ et $z.$

Comme les cosinus directeurs du rayon lumineux sont d’après ce que nous venons de voir proportionnels à $\mu ,\,\mu '$ et $\mu ''\,;$ la droite $\mathrm {OO} '$ de la figure 21 est bien parallèle au rayon lumineux ; ce qui est conforme au résultat où nous avait conduits l’application du principe de Huyghens.

DOUBLE RÉFRACTION DANS LES CRISTAUX HÉMIÈDRES

190. Équations du mouvement. — Les théories de la double réfraction précédemment exposées ne s’appliquent qu’aux milieux holoèdres. Pour l’explication des phénomènes présentés par les milieux biréfringents hémièdres, nous devons, comme nous l’avons fait dans la théorie de la polarisation rotatoire, rejeter l’hypothèse du § 14, où nous admettions que dans les expressions de $\mathrm {D\xi ,\,D\eta ,\,D\zeta }$ les termes contenant les carrés de $\mathrm {D} x,\,\mathrm {D} y,\,\mathrm {D} z$ étaient négligeables. Nous avons vu que si l’on n’accepte pas cette hypothèse, la fonction $\mathrm {W} _{2}$ est une fonction homogène et du second degré des dérivées partielles des divers ordres de $\xi ,\,\eta ,\,\zeta$ et que les équations du mouvement sont

${\begin{aligned}\rho \,{\frac {d^{2}\xi }{dt^{2}}}&=\mathrm {P} ,&\rho \,{\frac {d^{2}\eta }{dt^{2}}}&=\mathrm {Q} ,&\rho \,{\frac {d^{2}\zeta }{dt^{2}}}&=\mathrm {R} ,\end{aligned}}$

$\mathrm {P,\,Q,\,R}$ étant des polynômes linéaires par rapport aux dérivées des divers ordres de $\xi ,\,\eta ,\,\zeta ,$ polynômes dont nous avons indiqué le mode de formation (124).

Si l’on ne tient pas compte de la dispersion il est inutile d’introduire les dérivées partielles du quatrième ordre. Posons donc

${\begin{aligned}\mathrm {P} &=\mathrm {X} +\mathrm {F} ,&\mathrm {Q} &=\mathrm {Y} +\mathrm {G} ,&\mathrm {R} &=\mathrm {Z} +\mathrm {H} ,\end{aligned}}$

$\mathrm {X,\,Y,\,Z}$ étant des fonctions linéaires des dérivées secondes de $\xi ,\,\eta ,\,\zeta$ et $\mathrm {F,\,G,\,H}$ des fonctions linéaires des dérivées du troisième ordre. En prenant des unités telles que $\rho$ soit égal à $1,$ les équations du mouvement sont alors

${\begin{aligned}{\frac {d^{2}\xi }{dt^{2}}}&=\mathrm {X} +\mathrm {F} ,\\[1.5ex]{\frac {d^{2}\eta }{dt^{2}}}&=\mathrm {Y} +\mathrm {G} ,\\[1.5ex]{\frac {d^{2}\zeta }{dt^{2}}}&=\mathrm {Z} +\mathrm {H} .\\\end{aligned}}$

Dans le cas des milieux holoèdres ces équations doivent nécessairement se réduire à celles que nous avons prises au commencement de ce chapitre et qui nous ont conduits à l’explication des phénomènes de double réfraction présentés par ces milieux. Montrons qu’en effet les quantités $\mathrm {F,\,G,\,H}$ disparaissent alors des équations précédentes.

Les milieux holoèdres possédant trois plans de symétrie optiques et par conséquent un centre de symétrie, les équations qui donnent le mouvement d’une de leurs molécules ne doivent pas changer quand on change les signes de $x,\,y,\,z,$ $\xi ,\,\eta ,\,\zeta .$ Or cette condition ne serait pas satisfaite si ces équations contenaient une dérivée du troisième ordre, ${\frac {d^{3}\xi }{dx^{2}dy}}$ par exemple, car cette dérivée conserverait son signe tandis que les dérivées ${\frac {d^{2}\xi }{dt^{2}}},\dots ,$ qui forment les premiers membres, en changeraient. D’ailleurs nous avons déjà dit (124) que d’une manière générale les équations du mouvement dans un milieu possédant un centre de symétrie ne pouvaient contenir que des dérivées d’ordre pair.

191. Les coefficients des différents termes des polynômes $\mathrm {F} ,$ $\mathrm {G} ,$ $\mathrm {H}$ ne sont pas indépendants ; nous allons montrer que si le polynôme $\mathrm {F}$ contient $\alpha {\frac {d^{3}\eta }{dx^{2}dy}},$ le polynôme $\mathrm {G}$ contient $-\alpha {\frac {d^{3}\xi }{dx^{2}dy}}\cdot$

D’après le mode de formation du polynôme $\mathrm {P}$ le terme $\alpha {\frac {d^{3}\eta }{dx^{2}dy}}$ de ce polynôme doit provenir du terme $\alpha {\frac {d\eta }{dx}}{\frac {d^{2}\xi }{dx\,dy}}$ ou $\alpha \eta '_{x}\xi _{xy}''$ de la fonction $\mathrm {W} _{2}.$ En effet si nous appliquons ce mode de formation nous devrons d’abord prendre la dérivée de ce terme par rapport à $\xi _{xy}'',$ ce qui donne $\alpha \eta '_{x},$ puis prendre la dérivée seconde de ce résultat par rapport à $x$ et à $y,$ ce qui donne $\alpha {\frac {d^{3}\eta }{dx^{2}dy}}\cdot$

Si maintenant nous cherchons les termes de $\mathrm {G}$ qui sont donnés par le terme $\alpha \eta '_{x}\xi _{xy}''$ de la fonction $\mathrm {W} _{2},$ l’un de ces termes s’obtiendra en dérivant d’abord par rapport à $\eta '_{x},$ puis en dérivant le résultat par rapport à $x$ et changeant le signe. En effectuant ces opérations on trouve comme nous l’avons annoncé, $-{\frac {\alpha d^{3}\xi }{dx^{2}dy}}\cdot$

192. Propagation d’une onde plane. — Étudions, en prenant pour point de départ les travaux de Neumann et de Mac-Cullagh, la propagation d’une onde plane dans un milieu hémièdre.

Les axes auxquels sont rapportées les équations du mouvement étant quelconques nous pouvons considérer l’onde plane comme parallèle au plan des $xy.$ Alors $\xi ,\,\eta ,\,\zeta$ ne dépendent plus que de $z$ et de $t,$ et les dérivées des déplacements par rapport à $x$ et $y$ disparaissent des équations du mouvement. Si les polynômes $\mathrm {F,\,G,\,H}$ étaient nuls, les vibrations seraient transversales ; la condition $\Theta =0$ donnerait ${\frac {d\zeta }{dz}}=0$ et les dérivées de $\zeta$ par rapport à $z$ disparaîtraient aussi des équations du mouvement. En général, quand $\mathrm {F,\,G}$ et $\mathrm {H}$ sont différents de zéro, il n’en est plus ainsi, mais les vibrations étant encore presque transversales on peut négliger ces dérivées.

Dans ces conditions les équations du mouvement dans le plan de l’onde sont

${\begin{aligned}{\frac {d^{2}\xi }{dt^{2}}}&=a\,{\frac {d^{2}\xi }{dz^{2}}}+b\,{\frac {d^{2}\eta }{dz^{2}}}+\alpha \,{\frac {d^{3}\xi }{dz^{3}}}+\beta \,{\frac {d^{3}\eta }{dz^{3}}},\\[1.5ex]{\frac {d^{2}\eta }{dt^{2}}}&=b\,{\frac {d^{2}\xi }{dz^{2}}}+c\,{\frac {d^{2}\eta }{dz^{2}}}-\beta \,{\frac {d^{3}\xi }{dz^{3}}}+\gamma \,{\frac {d^{3}\eta }{dz^{3}}}\,;\\\end{aligned}}$

équations dans lesquelles les coefficients satisfont aux relations

imposées par le mode de formation des seconds

membres.

Elles se simplifient quand on prend pour axes des $x$ et des $y$ les directions rectangulaires des deux vibrations de Neumann. Elles doivent alors être satisfaites pour les valeurs de $\xi$ et $\eta$ correspondant à ces vibrations quand on néglige les dérivées du troisième ordre. Or si on fait $\xi =\mathrm {A} e^{{\frac {2i\pi }{\lambda }}(z-\mathrm {V} t)},$ $\eta =0,$ coordonnées de l’extrémité de la vibration parallèle à l’axe des $x,$ la seconde donne $b=0.$ Par conséquent, par ce choix d’axes de coordonnées les équations précédentes se réduisent à

${\begin{aligned}{\frac {d^{2}\xi }{dt^{2}}}&=a\,{\frac {d^{2}\xi }{dz^{2}}}+\alpha \,{\frac {d^{3}\xi }{dz^{3}}}+\beta \,{\frac {d^{3}\eta }{dz^{3}}}\\[1.5ex]{\frac {d^{2}\eta }{dt^{2}}}&=c\,{\frac {d^{2}\eta }{dz^{2}}}-\beta \,{\frac {d^{3}\xi }{dz^{3}}}+\gamma \,{\frac {d^{3}\eta }{dz^{3}}}\cdot \\\end{aligned}}$

193. En faisant des hypothèses particulières sur les coefficients des termes de $\mathrm {W} _{2}$ qui contiennent des dérivées secondes et qui, par conséquent, donnent les termes $\mathrm {F,\,G,\,H}$ des équations du mouvement, Mac-Cullagh est arrivé à des équations dans lesquelles $\alpha =\gamma =0.$ Nous allons montrer que sans faire aucune hypothèse sur la fonction $\mathrm {W} _{2}$ on a toujours $\alpha =\gamma =0.$

D’après le mode de formation des seconds membres des équations du mouvement le terme de $\mathrm {W} _{2}$ qui pourrait donner $\alpha {\frac {d^{3}\xi }{dz^{3}}}$ dans $\mathrm {F}$ devrait être de la forme $\alpha {\frac {d\xi }{dz}}{\frac {d^{2}\xi }{dz^{2}}}$ ou $\alpha \xi '_{z}\xi _{z}''.$ Cherchons les deux termes qu’il donnera dans $\mathrm {F} .$ Nous aurons :

${\begin{aligned}\mathrm {F} =-{\frac {d}{dz}}{\frac {d\alpha \xi _{z}'\xi _{z}''}{d\xi '_{z}}}&+{\frac {d^{2}}{dz^{2}}}{\frac {d\alpha \xi _{z}'\xi _{z}''}{d\xi _{z}''}}+\dots \\[1.5ex]\mathrm {F} =-{\frac {d}{dz}}\alpha \xi _{z}''&+{\frac {d^{2}}{dz^{2}}}\alpha \xi '_{z}+\dots ,\\\end{aligned}}$

ou

$\mathrm {F} =-\alpha \,{\frac {d^{3}\xi }{dz^{3}}}+\alpha \,{\frac {d^{3}\xi }{dz^{3}}}+\ldots$

Par conséquent le seul terme de $\mathrm {W} _{2}$ pouvant donner un terme en ${\frac {d^{3}\xi }{dz^{3}}}$ dans la première équation en donne deux qui se détruisent. On verrait de la même manière que ${\frac {d^{3}\eta }{dz^{3}}}$ ne doit pas entrer dans la seconde équation. On a donc pour ces équations

(1)

${\begin{aligned}{\frac {d^{2}\xi }{dt^{2}}}&=a\,{\frac {d^{2}\xi }{dz^{2}}}+\beta \,{\frac {d^{3}\eta }{dz^{3}}}\\[1.5ex]{\frac {d^{2}\eta }{dt^{2}}}&=c\,{\frac {d^{2}\eta }{dz^{2}}}-\beta \,{\frac {d^{3}\xi }{dz^{3}}}\\\end{aligned}}$

194. Vitesses de propagation. — Cherchons à satisfaire à ces équations en posant

$\xi =\mathrm {A} e^{{\frac {2i\pi }{\lambda }}(z-\mathrm {V} t)},\qquad \eta =\mathrm {B} e^{{\frac {2i\pi }{\lambda }}(z-\mathrm {V} t)}.$

Nous obtiendrons en substituant et divisant par ${\frac {2i\pi }{\lambda }},$

${\begin{aligned}\mathrm {AV} ^{2}&=a\mathrm {A} +{\frac {2i\pi }{\lambda }}\beta \mathrm {B} ,\\[1.5ex]\mathrm {BV} ^{2}&=c\mathrm {B} -{\frac {2i\pi }{\lambda }}\beta \mathrm {A} \,;\\\end{aligned}}$

et en remplaçant ${\frac {2\pi }{\lambda }}\beta$ par $\beta '$,

(2)

${\begin{aligned}\mathrm {AV} ^{2}&=a\mathrm {A} +i\beta '\mathrm {B} ,\\[1.5ex]\mathrm {BV} ^{2}&=c\mathrm {B} -i\beta '\mathrm {A} \,;\\\end{aligned}}$

Nous tirons de ces équations

${\begin{aligned}(\mathrm {V} ^{2}-a)\mathrm {A} &=i\beta '\mathrm {B} ,\\(\mathrm {V} ^{2}-c)\mathrm {B} &=-i\beta '\mathrm {A} ,\\\end{aligned}}$

et en multipliant ces deux dernières nous obtenons

(3)

$(\mathrm {V} ^{2}-a)(\mathrm {V} ^{2}-c)=\beta '^{2}\cdot$

Cette équation nous donne deux valeurs pour la vitesse de propagation de l’onde, et ces valeurs sont réelles, car $\beta$ étant très petit, $\beta '$ l’est aussi ; nous aurons donc deux rayons lumineux. Ces vitesses deviennent égales $\textstyle \mathrm {V} ={\sqrt {a\pm \beta '}}$ quand on a $a=c.$ Dans le cas général, l’une d’elles est très voisine de $\textstyle {\sqrt {a}},$ l’autre de $\textstyle {\sqrt {c}}.$

195. Polarisation elliptique des rayons. — La seconde des équations (2) nous donne

${\frac {\mathrm {B} }{\mathrm {A} }}={\frac {-i\beta '}{\mathrm {V} ^{2}-c}}\,;$

elle nous montre que le rapport ${\frac {\mathrm {B} }{\mathrm {A} }}$ est une quantité purement imaginaire. Si donc nous supposons $\mathrm {A}$ réel, $\mathrm {B}$ est de la forme $\mathrm {B} =i\mathrm {B_{1}}$ et les parties réelles de $\xi$ et $\eta$ qui satisfont aux équations du mouvement sont

${\begin{aligned}\xi &=\;\;\mathrm {A} \;\;\cos {\frac {2\pi }{\lambda }}(z-\mathrm {V} t),\\[1.5ex]\eta &=-\mathrm {B} _{1}\sin {\frac {2\pi }{\lambda }}(z-\mathrm {V} t).\\\end{aligned}}$

La trajectoire de la molécule vibrante est donnée par l’équation

${\frac {\xi ^{2}}{\mathrm {A} ^{2}}}+{\frac {\eta ^{2}}{\mathrm {B} _{1}^{2}}}=1$

qui est celle d’une ellipse rapportée à ses axes. Par conséquent, dans les cristaux hémièdres, les rayons sont polarisés elliptiquement et les axes de l’ellipse de polarisation sont les directions de vibrations des rayons polarisés rectilignement dans le cristal holoèdre.

Le rapport des axes de l’ellipse est égal à

$-{\frac {\mathrm {B} _{1}}{\mathrm {A} }}={\frac {\beta '}{\mathrm {V} ^{2}-a}}\cdot$

En élevant au carré et remplaçant $\beta '^{2}$ par sa valeur (3), nous obtenons pour le rapport des carrés des axes.

$\mathrm {R} ={\frac {\mathrm {V} ^{2}-c}{\mathrm {V} ^{2}-a}}\cdot$

Pour l’onde dont la vitesse de propagation est voisine de ${\sqrt {a}},$ le numérateur de $\mathrm {R}$ est voisin de $a-c,$ et le dénominateur voisin de $0\,;$ la valeur de $\mathrm {R}$ est donc très grande, et l’ellipse est très allongée. — Pour l’onde dont la vitesse de propagation est voisine de ${\sqrt {c}},$ $\mathrm {R}$ est voisin de zéro, et l’ellipse est encore très allongée. Par conséquent, en général, la polarisation des deux rayons réfractés sera presque rectiligne. Pour que la polarisation elliptique soit appréciable, il faut que la différence $a-c$ soit très petite ; dans ce cas, en effet, les deux termes du rapport $\mathrm {R}$ étant très petits, ce rapport aura une valeur finie.

Considérons le cas où $c=a.$ Si on néglige les termes contenant $\beta '$ en facteur, les deux équations (2) deviennent

$\mathrm {AV} ^{2}=\mathrm {A} a\qquad \qquad \mathrm {BV} ^{2}=\mathrm {B} a$

et le rapport ${\frac {\mathrm {B} }{\mathrm {A} }}$ est indéterminé ; la polarisation est rectiligne, mais le plan de polarisation est indéterminé. La direction de propagation est donc un axe optique du cristal. D’après ce qui précède, la polarisation elliptique ne sera sensible dans un cristal hémièdre que lorsque la direction de propagation sera voisine de l’axe optique, puisque dans ces conditions seulement $a-c$ sera très petit.

Si l’on considère une onde plane dont la direction de propagation dans un cristal hémièdre est celle de l’axe optique, elle donnera naissance à deux ondes planes, puisque les vitesses de propagation $\textstyle {\sqrt {a+\beta '}}$ et $\textstyle {\sqrt {a-\beta '}}$ de ces ondes sont différentes. En outre, ces deux ondes seront polarisées circulairement, car le rapport $\mathrm {R}$ des carrés des axes de l’ellipse devient alors ${\frac {\mathrm {V} ^{2}-a}{\mathrm {V} ^{2}-a}}=1.$ On aura donc le phénomène de la polarisation rotatoire.

196. Reprenons le cas où les deux ondes se propagent avec des vitesses différentes que nous désignerons par $\mathrm {V} '$ et $\mathrm {V} '',$ et où les rayons sont polarisés elliptiquement. Montrons que les ellipses décrites par la molécule vibrante dans les deux ondes planes sont égales.

Si nous supposons que $\mathrm {V} '$ soit la vitesse la plus voisine de ${\sqrt {a}},$ le rapport $\mathrm {R}$ des carrés des axes de l’ellipse qui correspond à cette vitesse sera plus grand que $1$ et représentera le carré du rapport du grand axe au petit axe ; la valeur de $\mathrm {R}$ est alors

${\frac {\mathrm {V} '^{2}-c}{\mathrm {V} '^{2}-a}}\cdot$

Pour l’autre vitesse $\mathrm {V} '',$ $\mathrm {R}$ est au contraire plus petit que l’unité, et le carré du rapport du grand axe au plus petit axe de l’ellipse correspondant à cette vitesse est

${\frac {\mathrm {V} ''^{2}-a}{\mathrm {V} ''^{2}-c}}\cdot$

Si les deux ellipses sont égales, nous devons avoir

${\frac {\mathrm {V} '^{2}-c}{\mathrm {V} '^{2}-a}}={\frac {\mathrm {V} ''^{2}-a}{\mathrm {V} ''^{2}-c}},$

ou

$\mathrm {V} '^{2}+\mathrm {V} ''^{2}=a+c.$

Or, si nous développons l’équation (3) qui donne les vitesses, nous obtenons

$\mathrm {V} ^{4}-(a+c)\mathrm {V} ^{2}+ac-\beta '^{2}=0,$

et nous avons bien pour la somme des racines $\mathrm {V} '^{2}$ et $\mathrm {V} ''^{2}$ de cette équation

$\mathrm {V} '^{2}+\mathrm {V} ''^{2}=a+c.$

Ces deux ellipses égales ont leurs grands axes perpendiculaires l’un à l’autre, puisque le rapport $\mathrm {R}$ du carré de l’axe dirigé suivant $\mathrm {O} x$ au carré de l’axe dirigé suivant $\mathrm {O} y,$ passe d’une valeur plus petite que $1$ à une valeur plus grande que $1,$ ou réciproquement quand on y fait successivement $\mathrm {V} ^{2}$ égal à $\mathrm {V} '^{2}$ et à $\mathrm {V} ''^{2}.$

Fig. 25. Enfin ces ellipses seront décrites en sens contraire, comme l’indiquent les flèches de la figure. Pour le faire voir, il suffit de montrer que le rapport ${\frac {\mathrm {B} _{1}}{\mathrm {A} }}$ des modules de $\eta$ et de $\xi$ change de signe avec le rayon considéré. Or, ce rapport a pour valeur ${\frac {\beta '}{\mathrm {V} ^{2}-c}},$ et il changera de signe si $c$ est compris entre les valeurs $\mathrm {V} '^{2}$ et $\mathrm {V} ''^{2}$ des carrés des vitesses. La substitution de $c$ à $\mathrm {V} ^{2}$ dans le premier membre de l’équation des vitesses

$(\mathrm {V} ^{2}-a)(\mathrm {V} ^{2}-c)-\beta '^{2}=0,$

donne un résultat négatif, tandis que si l’on fait $\mathrm {V} ^{2}=\infty$ et $\mathrm {V} ^{2}=0,$ on obtient une quantité positive. L’une des racines est donc plus grande que $c,$ l’autre plus petite.

197. Il est possible en parlant des hypothèses de M. Sarrau d’expliquer les phénomènes de double réfraction dans les milieux hémièdres. Nous n’insisterons pas sur cette théorie, et nous renverrons au mémoire que M. Potier a publié sur ce sujet dans le Bulletin de l’Association française pour l’avancement des sciences (t. I, p. 264).

---

1. Œuvres complètes de Fresnel, t. II, p. 261.