L’Algèbre d’Omar Alkhayyami/C
C
« Je dis (**[1]). Et Aboû Sahl Vîdjan Ben Vastem Alqoûhî est auteur d’un mémoire qu’il composa dans le but de combler la lacune qui se trouve dans le second livre de l’ouvrage d’Archimède. Il a dit dans ce mémoire qu’il y a là trois constructions qui rentrent dans la même catégorie, dont la première est celle d’un segment de sphère qui, de deux autres segments de sphère, est égal à l’un et semblable à l’autre. La seconde, celle d’un segment de sphère dont la surface est égale à celle d’un autre segment de sphère, et qui est semblable à un second segment de sphère. La troisième, celle d’un segment de sphère égal à un autre segment de sphère, et dont la surface est égale à celle d’un second segment de sphère. Archimède résolut les deux premiers problèmes sans s’occuper du troisième, qui ne fut pas ajouté non plus aux deux autres par les géomètres qui lui succédèrent. Ensuite il (Alqoûhî) en donna la construction et la démonstration de la manière suivante. »
Énonçons avec un peu plus de précision et puis examinons préalablement les trois problèmes en question.
I. Construire un segment de sphère égal en volume à un segment de sphère donné, et semblable à un second segment de sphère donné. (Archim., Sph. et Cyl., II, 6.)
II. Construire un segment de sphère égal en surface (*[2]) à un segment de sphère donné, et semblable à un second segment de sphère donné. (Archim., Sph. et Cyl., II, 7.)
III. Construire un segment de sphère égal en volume à un segment de sphère donné, et égal en surface à un second segment de sphère donné. (Alqoûhî.)
Désignons le rayon de la sphère à laquelle appartient le segment qu’il s’agit de construire par , la distance du plan coupant au pôle du segment par Δ, on aura :
I. Δ Δ) , Δ/r ... Δ II. Δ , ... , Δ =
III. 1) Δ Δ, Δ .
Posons , ; il suit
3) Δ Δ + 3 a' b' = 0, 4) .
Comme il faut exclure les valeurs négatives de r et de Δ, et parmi les valeurs positives celles qui rendraient Δ (*[3]), on trouve :
1° Que le problème n’a de solution que tant que ;
2° Que lorsque , le segment cherché est l’hémisphère (**<ref>**) Les deux équations se décomposent, en ce cas, de la manière suivante :
(Δ - (Δ et .
3° Que pendant que , on obtient deux segments, dont l’un est plus et l’autre moins grand que la moitié de la sphère ;
4° Que lorsque , il existe deux solutions dont l’une donne une sphère entière, l’autre un segment dont la hauteur rapportée à l’unité du rayon est égale à 0,268 environ ;
5° Enfin, que lorsque , il n’y a qu’une seule solution et un seul segment plus petit que la moitié de la sphère.
Cet exposé rapide fait voir que le problème que se propose Alqoûhî est d’une difficulté supérieure aux deux premiers résolus par Archimède. Ce n’est même que grâce à la forme particulière des équations 1) et 2), que le problème ne conduit pas à une équation du sixième degré. Or le géomètre arabe ne résout pas seuleme.nt le problème, mais il en discute encore les cas particuliers tout aussi complétement qu’on vient de le faire. Pour arriver à ce résultat, il s’y prend de la manière suivante :
Il construit deux cônes tels que le premier soit égal en volume au premier segment de sphère donné, et que le second ait pour hauteur et pour rayon de sa base une droite égale à la droite HN, menée du pôle du second segment de sphère donné à un point quelconque de la circonférence de sa base (*[4]). En désignant les volumes de ces deux cônes par C et C' respectivement, on aura et
, .
Ensuite il prend une ligne et une ligne . Avec ces données il construit deux coniques,
une hyperbole équilatère x . y = \overline{\text{HN}}^2
et une parabole .
L’intersection de ces deux coniques a pour ordonnée la hauteur du segment qu’il s’agit de construire, et pour abscisse le diamètre de la sphère à laquelle ce segment appartient (**[5]).
Ce qu’il y a de remarquable ici, c’est la construction simultanée de deux équations renfermant deux inconnues, par l’intersection de deux coniques. Mais passons à la discussion, bien plus intéressante, que le géomètre arabe fait des cas particuliers. Alqoûhî distingue ces cas suivant les différentes valeurs que peut prendre le rapport , à savoir :
, , ;
ce qui équivaut à
, , .
Il démontre d’abord d’une manière rigoureuse, par la considération de la tangente commune, qu’au cas du contact des deux coniques on a ; ensuite qu’on a généralement , et que le dénominateur de cette dernière expression devenant un maximum au cas du contact, puisque alors , la valeur \tfrac{\sqrt{2}}{1} correspondant au cas du contact sera la valeur minimum du rapport , et la limite qu’il ne peut pas surpasser en petitesse.
Il démontre ensuite, d’une manière non moins rigoureuse et non moins purement géométrique, que tant que Δ > r, on aura ; d’où il suit que le segment qu’il s’agit de construire doit être plus grand que l’hémisphère, le rapport donné a pour limite supérieure .
L’auteur constate encore que lorsque le segment est plus petit que l’hémisphère, le rapport n’a pas de limite supérieure, et que de ce qui précède il suit qμ’aux valeurs de comprises entre et peuvent correspondre des segments dans les deux moitiés de la sphère.
Mais le passage qui se rapporte à cette discussion me semble trop important pour que je puisse, malgré sa longueur, me dispenser d’en donner la traduction textuelle.
Après avoir terminé l’analyse (*[6]) du problème, l’auteur s’exprime ainsi :
« Et nous disons : Le rapport du cône de la surface au cône du segment (**[7]) ne peut pas être un rapport quelconque, mais il existe nécessairement pour lui une limite de petitesse qu’il ne surpassera pas, et qui correspond au contact des deux sections coniques en M (fig. 36). Menons (en ce cas) la droite OML touchant les deux sections coniques et passant par leur point de contact. A cause de l’hyperbole on aura OM égale à ML, comme c’est démontré dans la troisième proposition du deuxième livre du traité des Sections Coniques (***[8]) ; donc, parce que DM et BO sont parallèles, LD sera égale à DB, c’est-à-dire au diamètre de la sphère. Et parce que ML est tangente à la parabole, LK sera égale à KD, en vertu de ce qui est démontré dans la trente-troisième proposition du premier livre du même traité (****[9]) ; conséquemment DK sera égale au rayon de la sphère, et le point K coïncidera avec le point E (*****[10]). Mais on vient d’expliquer ci-dessus que le rapport du cône de la surface au cône du segment est égal au rapport du rectangle AB en BK au rectangle BZ en BE (*[11]), c’est-à-dire BZ en BK, qui est égal au rapport de AB à BZ. Le rapport de ces cônes étant égal aussi au rapport de AB à S (**[12]), on aura BZ, c’est-à-dire DM égale à S ; et le rectangle S en DK étant égal au carré de DM (***[13]), DK sera égale à DM, c’est-à-dire à BZ ; d’où il suit que BZ et pareillement AZ seront égales au rayon de la sphère. Le rapport du cône de la surface au cône du segment, qui est égal au rapport de AB à BZ, sera donc en ce cas égal au rapport qui multiplié en lui-même produit le rapport de deux à un, parce que le rapport de AB à BZ multiplié en lui-même est égal au rapport de DB à BZ. Ce rapport, qui multiplié en lui-même est égal au rapport de deux à un, est le ràpport de deux à sa racine, ou le rapport de la racine de deux à l’unité. Le rapport dont il s’agit (****[14]) ne peut donc pas être plus petit que cela ; car le rapport du rectangle AB en BD au rectangle BZ en ZE, qui est égal au rapport du cône de la surface au cône du segment (****[15]), est composé du rapport de AB à BZ, c’est-à-dire du rapport de DB à BA, et du rapport de BD à ZE ; de sorte qu’il est égal au rapport du carré de BD au rectangle AB en ZE. Prenant BD comme hauteur commune, le rapport du cône de la surface au cône du segment sera égal au rapport du cube de BD au solide AB en ZE en BD : en même temps, donnant aux rectangles AB en BD, et BZ en ZE, la hauteur commune ZK, on aura le rapport du cône de la surface au cône du segment égal au solide AB en BD en ZB au solide ligne BZ en carré de EZ ; donc, ex œquo, le rapport du cube de BD au solide ligne BZ en carré de ZE, égal au rapport du oône de la surface au cône du segment multiplié en lui-même (*[16]). Mais le solide ligne BZ en carré de ZE est un maximum lorsque BZ est la moitié de ZE, comme il est démontré dans ce que nous avons rapporté (**[17]) suivant Eutocius, à l’aide des sections coniques ; cependant noua en donnerons plus tard une démonstration indépendante des sections coniques. Le rapport du cube de BD au solide ligne BZ en carré de ZE est donc un minimum lorsque BZ est égale au rayon de la sphère ; et si le cône de la surface est considéré comme invariable, le segment sera un maximum en ce cas. »
« Relativement à la grandeur, le rapport dont il s’agit n’aura pas de limite lorsque le segment est plus petit que la moitié de la sphère. »
« Lorsque, au contraire, le segment est plus grand que la moitié de la sphère (***[18]), ce rapport ne peut pas être plus grand que celui de deux à un. Car le rectangle AB en BD est plus petit que le carré de BD ; conséquemment le rapport du rectangle AB en BD au rectangle BZ en ZE, sera plus petit que le rapport du carré de BD au rectangle BZ en ZE ; Z étant (en ce cas) plus voisin du milieu de BE que D, le rectangle BZ en ZE sera plus grand que le rectangle BD en DE, et le rapport du carré de BD au rectangle BZ en ZE plus petit que le rapport du carré de BD au rectangle BD en DE. Conséquemment le rapport du rectangle AB en BD au rectangle BZ en ZE, c'est-à-dire le rapport du cône de la surface au cône du segment plus petit de beaucoup que le rapport du carré de BD au rectangle BD en DE, c'est-à-dire que le rapport de BD à DE, qui est égal au rapport de deux à un. Le rapport de deux à un est donc la limite que ce rapport () ne peut pas surpasser en grandeur ; et si nous considérons le cône de la surface comme invariable, le segment sera un minimum en ce cas. »
« De ce que nous venons de dire, il résulte que le rapport de deux à sa racine est le minimum de tous la rapports qui ont lieu dans la sphère entre le cône de la surface et le cône du segment ; que les rapports compris entre lui et le rapport de deux à un peuvent correspondre à des segments dans les deux moitiés de la sphère ; et que des rapports de deux à une quantité plus petite que l'unité, aucun ne correspond à la partie qui est plus grande que la moitié, mais qu'ils appartiennent tous exclusivement à la partie qui est plus petite que la moitié. »
Cette discussion est suivie de la synthèse du problème et de la démonstration de la synthèse. Celle-ci terminée, l'auteur considère une seconde fois les cas particuliers ; je reproduis textuellement le passage qui contient cette seconde discussion, ou plutôt ce résumé, dans lequel l'auteur établit les mêmes catégories auxquelles on a été conduit ci-dessus (pag. 105) par les méthodes modernes.
« De ce que nous avons dit, il résulte que lorsque le rapport mentionné (*[19]) est plus petit que le rapport de deux à sa racine, le problème ne peut pas avoir de solution ; mais lorsqu’il n’est pas plus petit que cela, la solution est possible. »
« D’abord, s’il est égal au rapport de deux à sa racine, les deux sections coniques se touchent uniquement au point M ; le segment cherché est égal à la moitié de la sphère, et pas à autre chose, et les deux points E, K deviennent identiques. »
« Lorsqu’il est plus grand que le rapport de deux à sa racine, et plus petit que le rapport de deux à un, les deux sections coniques se coupent en deux points ; et lorsque de ces deux points deux perpendiculaires sont abaissées sur BK, les deux abscisses correspondant aux deux perpendiculaires sont justes toutes les deux, et seront diamètres de la sphère. pour l’une d’elles le segment cherché est plus petit que la moitié de la sphère, et c’est le cas lorsque la perpendiculaire qui termine le diamètre de la sphère est abaissée de celui des deux points d’intersection qui est le plus éloigné du point B ; le point E en ce cas est situé en dehors de la ligne comprise entre les deux points B et K. Relativement à l’autre, le segment sera plus grand que la moitié de la sphère, et c’est le cas lorsque la perpendiculaire dont il s’agit est abaissée du point d’intersection le plus voisin de B ; le point E en ce cas est situé entre les deux points B et K. »
« Lorsque ce rapport est égal au rapport de deux à un, l'abscisse déterminée sur BK par la perpendiculaire la plus voisine de B, est égale à AB, et le segment est le plus grand de tous ceux qui existent sur la sphère. Quant à l’abscisse déterminée par la perpendiculaire la plus éloignée, le segment cherché de la sphère qui lui correspond est plus petit que la moitié, et la flèche du segment est un huitième à peu près du diamètre de la sphère, ou plutôt plus grande (*[20]) que cela d’une petite quantité, ce qu’on détermine à l’aide de l’istikrâ (**[21]) et du calcul. »
« Enfin lorsqu’il est plus grand que le rapport de deux à un, la partie de BK coupée par la perpendiculaire la plus voisine n’est plus juste, parce qu’elle doit représenter le diamètre de la sphère, et que pourtant AB serait plus grande qu’elle ; au contraire, la partie coupée par la perpendiculaire la plus éloignée de B est seule juste à cause de cela ; le segment (qui lui correspond) sera plus petit que la moitié (de la sphère), et sa flèche plus petite que le rayon (***[22]). »
« Dans tous les cas, AB sera invariable. »
Voici enfin la démonstration élémentaire du théorème d’Eutocius, que l’auteur avait annoncée ci-dessus (pag. 110, lig. 12), et qu’il donne en effet de la manière suivante.
Il prend sur la droite AC (fig. 37) un point B, de sorte que , et prolonge AC d’une partie CE = BC. Puis, en prenant un point D situé 1° entre A et B, 2° entre B et C, il démontre que dans les deux cas on aura .
Premier cas. On a , donc . Mais (parce que B est plus voisin du milieu de AE que D). Conséquemmentd’où il suit
donc
AB . > AD . DC, c. q. f. d.
Second cas. AB . BE = 2 < AD . DE,
conséquemment
d’où il suit
- ↑ **) On voit que ce n’est qu’une reproduction ou un extrait du traité original d’Alqoûbi. En effet, ce morceau, qui dans le ms. de la bibliothèque de Leyde est isolf, fait partie, dans le ms. de la Bibliothèque nationale, d’une traduction ou plutôt d’une édition arabe du traité de la sphère et du cylindre d’Archimède. Dans une courte préface, l’auteur, qui d’ailleurs ne se nomme pas, dit qu’il a fait cette édition 1° d’après un exemplaire de l’édition vulgaire de ce traité, mal traduit d’abord, revu et corrigé ensuite par Thâbit Ben Korrah, duquel il s’est efforcé d’éliminer les fautes qui s’étaient glissées par l’ignorance du copiste ; 2° d’après une traduction du commentaire d’Eutocius, faite avec soin et intelligence par Isbàk Ben Honaïn, auquel commentaire se trouvait entremêlé le texte du traité d’Archimède. De plus, il y était joint séparément le texte du premier livre jusqu’à la quatorzième proposition, traduit de même par Ishâk. L’éditeur dit encore avoir donné des explications qui lui sont propres, et avoir mis à contribution les ouvrages d’autres géomètres pour éclaircir les endroits difficiles ; enfin il nous avertît que le nombre des propositions du premier livre, dans l’exemplaire de ThAbit, était quarante-huit ; dans celui d’Ishâk, quarante-trois ; et qu’il a jugé convenable de joindre à la fin du traité le livre de la mesure du cercle par Archimède. — L’ouvrage original d’Alqoûhi est mentionné dans le passage du Qitâb Alfihrisi cité ci-dessus (p. 55, 1. 19).
- ↑ *) Dans la surface du segment la base circulaire n'est pas comprise.
- ↑ *) On discute facilement les deux équations proposées sous ce dernier rapport, en y substituant l à r, ce qui change la condition dans Δ (3 - Δ), et en examinant ensuite, à l’aide du théorème de M. Sturm, le nombre des racines réelles de l’équation Δ - 6 Δ + 9 Δ (où ) comprises dans les deux intervalles de 0 à + 1 et de + l à + 2, en distinguant pour le second intervalle les cas , et ; dans ce dernier cas on aura Δ Δ + 9 Δ - 2 = (Δ - 2) . (Δ Δ .
- ↑ *) On voit aisément que la longueur de cette droite est constante pour tous les segments de spère égaux en surface.
- ↑ **) En effet, en éliminant alternativement x et y entre les équations des deux sections coniques, après y avoir substitué à HN, BK, S leurs valeurs en a' et b', on aura
5) , 6) .
Ces équations, comparées aux équations 3) et 4), montrent immédiatement que y répond à Δ et x à 2r. - ↑ *) Dans l’acception ancienne de ce mot.
- ↑ **) C’est ainsi que l’auteur nomme les deux cônes dont nous avons désigné les volumes par C’et C respectivement.
- ↑ ***) Apollon., éd. d’Oxf., page 108.
- ↑ ****) Apollon., éd. d’Oxf., page 59.
- ↑ *****) On avait déterminé le point E en prenant sur le prolongement du diamètre BD, à partir du point D, un segment DE égal au rayon.
- ↑ *) ; on vérifie cela aisément au moyen des relations proposées ci-dessus, page 106.
- ↑ **) Voyez page 106, ligne 14, et la première note de la même page.
- ↑ ***) A cause de la parabole ; voir page 106, lig. 16.
- ↑ ****) .
- ↑ *****) Dans ce qui précède, l’auteur avait obtenu cette relation de la manière suivante. En prenant un segment TZ tel que , il avait (voir Archim., Sph. et Cyl. ii, 3, éd. d’Oxf., page 150) ; d’un autre c4té, il avait . Mais , donc ; et puisqu’il avait fait , il suit : ; c. q. f. d.
- ↑ *) Voici le raisonnement de l’auteur :
et en même temps , donc - ↑ **) Je rappelle que ce morceau faisait partie d’une édition arabe du traité de la sphère et du cylindre, en sorte qu’il avait été précédé de la cinquième proposition du second livre, et du commentaire d’Eutocius qui s’y rapporte. Voir la démonstration donnée par Eutocius, éd. d’Oxf., page 166, ligne 25 du texte grec, sqq.
- ↑ ***) Supposant BZ > Γ, on aura ; donc 1) ; en même temps , donc 2) ; de 1) et 2) il suit
- ↑ *) .
- ↑ *) Les deux manuscrits portent « plus petit, » et le manuscrit parisien, au lieu de
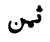 « un huitième », porte
« un huitième », porte  « un troisième ».
« un troisième ».
- ↑ **) Ici ce terme me parait indiquer des essais successifs, une sorte d’interpolation. (Voir la note de la page 10.)
- ↑ ***) Les deux manuscrits portent
 « le diamètre », au lieu de
« le diamètre », au lieu de 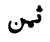 .
.






![{\displaystyle r={\sqrt[{3}]{\tfrac {3a}{\pi c^{2}(3-c)}}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/88a5cca494e9dfbf5187ad5b3a557cd17182a4ee)
![{\displaystyle ={\sqrt[{2}]{\tfrac {3ac}{\pi (3-c)}}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/a61bbc2a9388fbcb8f56b1821777411ec19cad26)




























































































