sine de B, est égale à AB, et le segment est le plus grand de tous ceux qui existent sur la sphère. Quant à l’abscisse déterminée par la perpendiculaire la plus éloignée, le segment cherché de la sphère qui lui correspond est plus petit que la moitié, et la flèche du segment est un huitième à peu près du diamètre de la sphère, ou plutôt plus grande (*[1]) que cela d’une petite quantité, ce qu’on détermine à l’aide de l’istikrâ (**[2]) et du calcul. »
« Enfin lorsqu’il est plus grand que le rapport de deux à un, la partie de BK coupée par la perpendiculaire la plus voisine n’est plus juste, parce qu’elle doit représenter le diamètre de la sphère, et que pourtant AB serait plus grande qu’elle ; au contraire, la partie coupée par la perpendiculaire la plus éloignée de B est seule juste à cause de cela ; le segment (qui lui correspond) sera plus petit que la moitié (de la sphère), et sa flèche plus petite que le rayon (***[3]). »
« Dans tous les cas, AB sera invariable. »
Voici enfin la démonstration élémentaire du théorème d’Eutocius, que l’auteur avait annoncée ci-dessus (pag. 110, lig. 12), et qu’il donne en effet de la manière suivante.
Il prend sur la droite AC (fig. 37) un point B, de sorte que , et prolonge AC d’une partie CE = BC. Puis, en prenant un point D situé 1° entre A et B, 2° entre B et C, il démontre que dans les deux cas on aura .
Premier cas. On a , donc . Mais (parce que B est plus voisin du milieu de AE que D). Conséquemment
- ↑ *) Les deux manuscrits portent « plus petit, » et le manuscrit parisien, au lieu de
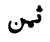 « un huitième », porte
« un huitième », porte  « un troisième ».
« un troisième ».
- ↑ **) Ici ce terme me parait indiquer des essais successifs, une sorte d’interpolation. (Voir la note de la page 10.)
- ↑ ***) Les deux manuscrits portent
 « le diamètre », au lieu de
« le diamètre », au lieu de 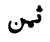 .
.






