À la surface des choses/L’énergie/Texte entier
es déformations diffuses de l’Espace autour des objets
qui s’attirent ou se repoussent ou se précipitent
l’un sur l’autre, les divers éléments secrets de toutes les
sortes de Matière, les Photons en mouvement éternel et les
messagers plus subtils que nous commençons seulement à
soupçonner, ne sont que les mille vêtements divers dont
peut s’envelopper une réalité protéiforme indestructible et
directement inaccessible à nos sens, substratum commun
VI
L’ÉNERGIE
TEMPÉRATURE
1. Échauffements produits par frottement. — Nous savons qu’un abaissement de poids (et plus généralement un travail moteur) ne peut se trouver réalisé « tout seul », mais nécessairement entraîne quelque répercussion qui ne se serait pas produite si le poids ne s’était pas abaissé. Cette répercussion peut être une élévation de poids (et plus généralement un travail résistant), élévation qui, elle aussi, ne se produit jamais « toute seule ». Nous savons que les « machines simples », telles que le treuil, permettent d’enchaîner, de conjuguer, une élévation de poids avec un abaissement de poids, sans que rien d’autre se produise, et qu’elles sont toutes équivalentes, en ce qu’aucune n’est plus avantageuse qu’une autre (Galilée). Sur ce Principe d’Équivalence entre les diverses façons d’obtenir du travail résistant et rien d’autre avec du travail moteur, nous avons édifié la théorie de l’équilibre des forces qui agissent sur un point, ou sur un système matériel[1].
Mais nous savons aussi qu’un poids peut s’abaisser avec un autre effet que d’en élever un autre, et qu’un travail moteur peut avoir d’autres répercussions qu’un travail résistant. Nous savons que, si nous forçons à glisser l’une sur l’autre deux surfaces solides appuyées l’une contre l’autre (comme dans les freins qu’on serre contre les roues d’un véhicule en mouvement), des forces engendrées par ce frottement apparaissent, qui luttent contre ce déplacement ; et que, en répercussion du travail moteur alors dépensé, les surfaces frottantes s’échauffent. De façon déjà presque appropriée aux mesures, quand le manège tournant de Rumford produisait un tel frottement au sein d’une grande cuve d’eau (XVIIIe siècle) le travail des chevaux n’élevait pas de poids, mais l’eau de la cuve se mettait à bouillir.
Nous voulons préciser cette corrélation ; pour cela, nous devrons d’abord approfondir quelque peu la notion familière d’échauffement.
2. Équilibre thermique. — Nos sensations de chaleur et de froid, que nous ne chercherons pas à définir, serviront de point de départ à cette analyse. Nous n’hésitons pas à reconnaître si notre main s’échauffe ou se refroidit. Partons de là.
Au contact de certains objets, pris en un état défini, notre main s’échauffe : nous dirons que ces objets sont « chauds ». Notre main s’échauffe d’ailleurs à distance en s’approchant des mêmes objets, sans les toucher : cet échauffement à distance est diminué ou empêché par interposition de certains « écrans ». De tels écrans, et notamment les écrans métalliques, permettent de définir des « rayons » calorifiques (qui en fait sont de la Lumière, généralement invisible). L’échauffement de notre main peut donc être produit par conductibilité, ou par rayonnement.
Symétriquement, nous disons que des objets sont « froids » si notre main se refroidit en les touchant (conductibilité) ou simplement en s’en approchant (rayonnement).
Enfin, nous appelons « tièdes » les objets que nous ne jugeons ni froids ni chauds.
Cette classification est grossière, particulièrement parce que notre organisme peut changer d’un instant à l’autre ; pourtant, même quand nous avons la fièvre, nous ne jugeons pas froide de l’eau bouillante. Contentons-nous, pour un instant, de ce moyen d’appréciation.
Alors que notre main, ou plutôt notre sang, demeure, tant que nous vivons, indéfiniment tiède au milieu d’objets que nous jugeons froids, il n’en est pas de même pour un objet tiède « inanimé », tel qu’une pierre. Mais un tel objet demeurera tiède, s’il est enfermé dans une enceinte close tiède en toutes ses parties, et qui ne se laisse pas traverser par du rayonnement calorifique.
Si alors on introduit dans cette enceinte un second objet tiède, rien ne se produit : deux objets « tièdes » mis en situation d’agir l’un sur l’autre par conductibilité ou par rayonnement, restent en « équilibre thermique » ; nous dirons que leur « température » est la même.
Considérons maintenant de la « glace fondante », c’est-à-dire de la glace finement pilée dont les interstices sont pleins d’eau liquide. Cette « glace fondante », qui pour notre main est « froide », constitue un objet thermiquement bien défini (beaucoup mieux que notre main), et nous pouvons, grâce à ce nouvel objet, et par des procédés analogues, opérer un classement semblable à celui qu’avaient permis les sensations de chaud et de froid de notre main (dont le rôle aura été de faire songer à un tel classement).
D’abord nous pourrons définir des objets en équilibre thermique avec la glace fondante : pour cela, nous réaliserons une « glacière », c’est-à-dire une cavité entourée de glace fondante (elle-même entourée d’une paroi métallique interceptant les rayonnements). Nous trouverons que certains de nos objets « froids » introduits dans cette glacière, n’y éprouvent aucun changement, et que les objets ainsi sélectionnés ne se modifient pas du fait qu’ils sont mis en situation d’agir l’un sur l’autre par conductibilité ou par rayonnement. Nous dirons que ces objets ont la même température, celle de la glace fondante.
Plus généralement, un objet ne peut subsister sans modification que s’il est dans une enceinte que l’extérieur ne peut modifier par contact ni rayonnement et qui pourrait être faite par de la matière identique à celle de l’objet, entourée d’un revêtement opaque. Tout deuxième objet alors introduit dans la même enceinte, au voisinage du premier et sans écran interposé, et qui n’y détermine pas de modification, sera dit à la même température.
3. Les températures peuvent être classées en une suite continue. — Nous pouvons maintenant classer toutes les températures, ainsi physiquement définissables, selon une série unique telle que, le long de l’un des deux sens dans lesquels on peut lire la série ? la température puisse être regardée omme de plus en plus élevée. Considérons, à cet effet, une température déterminée, celle de la glace fondante par exemple. Plaçons dans notre glacière un petit objet témoin qui a cette température ; rien ne se passe. Introduisons dans cette enceinte, au contact ou près de l’objet témoin et sans écran interposé, un second objet de température différente (disons du platine en fusion) ; notre témoin change, prenant une suite d’états parmi lesquels nous noterons un état encore infiniment voisin, pour toutes ses propriétés, de l’état initial. Et soit le témoin tel (cas ordinaire) qu’il reprend cet état initial quand on retire l’objet influençant (une plaque photographique ne conviendrait pas).
Recommençons l’expérience avec des objets de toutes les températures possibles, agissant successivement sur l’objet témoin, pris toujours dans le même état initial . Deux éventualités se présenteront :
1o Ou bien le point matériel témoin changera de manière à passer par l’état ; c’est ce qui arrivera, par exemple, si l’autre objet est tiède, ou s’il est à la température du mercure bouillant, ou s’il est à la température de l’argent fondant ; et dans tous ces cas nous dirons que l’écart de sa température avec celle de la glace fondante est de même sens ; de façon plus précise (et parce que la glace fondante est jugée froide par notre main qui est tiède) nous dirons que le second objet est « plus chaud » que l’objet témoin, ou encore que sa température est « plus élevée » que celle de la glace fondante.
2o Ou bien le point matériel témoin ne passera pas par l’état ; alors il passera toujours par un certain état très voisin aussi de l’état initial mais où certaines au moins des propriétés (telles que densité, viscosité, indice de réfraction, etc.), et généralement toutes, ont varié dans le sens inverse de celui où elles avaient varié entre et ; et nous dirons que la température du second objet est « plus basse » que celle de la glace fondante.
Ainsi la température de la glace fondante, choisie arbitrairement, partage en deux groupes l’ensemble des autres températures, le groupe qui contient la température de l’eau bouillante étant celui des températures plus élevées, et l’autre groupe étant celui des températures moins élevées.
Considérons maintenant une des températures plus élevées que celle de la glace fondante, disons celle de l’eau bouillante. Employant une étuve à eau bouillante au lieu de glacière, mais exactement de la même manière par considération du sens de la variation d’un objet témoin, nous partagerons en deux groupes les températures autres que celle de l’eau bouillante : et l’expérience montre que celui de ces deux groupes qui contient la température de la glace fondante (déjà classée comme moins élevée que celle de l’eau bouillante) contient aussi toutes les températures précédemment classées comme inférieures à celle de la glace fondante ; nous dirons que toutes les températures de ce groupe sont inférieures à celle de l’eau bouillante. Celles de l’autre groupe seront dites plus élevées.
Nous trouverons ensuite, toujours par expérience, que nous pouvons procéder de même pour toute température moins élevée que celle de la glace fondante, disons pour celle du mercure fondant, et celui des deux nouveaux groupes ainsi définis qui ne contiendra pas celle de la glace fondante formera le groupe des températures inférieures à celle du mercure fondant.
Ce genre d’expériences, indéfiniment poursuivi, permettra, de proche en proche, et sans contradiction, d’ordonner les températures en une série unique où toute température physiquement définissable trouvera sa place, une température étant plus élevée qu’une température si l’écart de avec est, dans la série, de même sens que l’écart de la température de l’eau bouillante avec celle de la glace fondante.
L’expérience montre que la série des températures ainsi définissables est physiquement continue. C’est-à-dire qu’il n’y a pas de température telle que le passage à une température supérieure détermine nécessairement une variation discontinue dans toutes les propriétés de toute substance.
Un caractère important est que, à mesure que la température s’élève, les propriétés des corps ne paraissent pas du tout s’approcher de propriétés limites, mais indiquent la possibilité d’un domaine infini de variation (voir VII, 28).
La notion physique de température est maintenant bien dégagée. Je n’ai pas su rattacher ce progrès au nom particulier d’aucun chercheur. La notion, certainement fort ancienne, a d’abord été confuse, et mêlée (comme il arrive encore chez les personnes peu instruites) avec d’autres notions que nous dégagerons, dans l’idée vague de « chaleur des corps ». Elle était certainement précisée avant le milieu du xviiie siècle.
4. Le frottement suffirait pour classer les températures. — Considérons les états successifs que prend une substance donnée, disons du mercure, à mesure que sa température s’élève. Chaque propriété de la substance, disons la densité, varie généralement alors toujours dans le même sens. Des exceptions se présentent pourtant (par exemple, pour l’eau, d’abord prise à la température de la glace fondante, et qu’on échauffe graduellement, la densité grandit, passe par un maximum, puis décroît).
Je veux faire observer que, pour une propriété au moins, la variation reste toujours de même sens : quand un objet est plus chaud qu’un autre, la variation qu’il y détermine par conductibilité ou par radiation pourrait toujours être obtenue en y dépensant du travail par frottement. On peut donc, réciproquement, de façon peut-être moins instructive, mais plus rapide, classer par ce seul moyen les températures en se bornant à dire, selon une règle qui ne comporte ni exceptions, ni contradictions :
Un corps est plus chaud qu’un autre s’il y détermine par contact ou rayonnement un changement qui pourrait y être produit par frottement[2].
5. Graduation des températures. — Nous allons maintenant « numéroter » les températures, faisant correspondre à chacune d’elles un nombre défini, qui sera « fonction » de la réalité physique « température ».
En principe, la loi de cette correspondance est arbitraire. Mais les conventions suivantes s’imposent :
D’abord, le nombre qui repère une température doit être d’autant plus grand que cette température est plus élevée ; c’est une fonction « croissante ».
Ensuite, cette fonction croissante doit être continue, en sorte que deux températures très voisines soient repérées par deux nombres très voisins.
Enfin, sans pouvoir encore mieux préciser, nous voudrons que des nombres franchement différents correspondent à des températures franchement différentes (c’est-à-dire entre lesquelles les propriétés des diverses substances changent notablement).
On peut satisfaire d’une infinité de manières à ces conditions ; par exemple, tant que le mercure reste liquide, et parce que son volume spécifique (volume de l’unité de masse) croît sans cesse avec la température, on pourra repérer la température par toute fonction continue, croissante et d’ailleurs quelconque de ce volume. Cette fonction cessera de convenir si le mercure se congèle, car il y a discontinuité entre les volumes spécifiques du mercure solide et du mercure liquide, alors pourtant qu’ils sont en équilibre thermique et qu’il faut par suite leur attribuer la même température. On devra, pour repérer les températures plus basses, choisir une nouvelle fonction assujettie aux mêmes conditions générales que la première et assujettie, de plus, à la prolonger. Ainsi pourra être définie de proche en proche une fonction numérique de la température. Cela d’une infinité de manières : nous verrons bientôt quel choix a paru le plus avantageux.
6. Isolement thermique. — La façon même dont nous avons pu définir la température montre que l’équilibre ne peut exister dans un système matériel que si la température y est partout la même, et que des transformations se produisent dès que cette uniformité est rompue. Transformations qui se poursuivent dans le sens d’un retour à l’uniformité : de deux corps mis en présence le plus chaud se refroidit, et le plus froid s’échauffe.
Il résulte de là que nous ne pouvons jamais isoler rigoureusement un objet au point de vue thermique, alors que nous pouvons y réussir au point de vue mécanique. Nous pouvons en effet l’enfermer dans une enceinte rigide, disons un récipient d’acier, qui ne se déforme pas, même durant un temps illimité, sous l’action de différences de pression toujours de même sens. Notons que si nous n’avions à notre disposition, comme corps « rigides », que de la poix ou de la cire, nous ne pourrions plus réaliser qu’un isolement mécanique approximatif, qui ne résisterait pas à une différence de pression, même faible, maintenue pendant un temps assez long.
Si on ne peut empêcher tout à fait, on peut, du moins pendant un temps fini, rendre pratiquement négligeables les actions qu’exercent, sur un système matériel, des corps extérieurs de température différente. On enfermera par exemple ce système dans un récipient de métal lui-même entouré d’une seconde enceinte métallique dont il est séparé par une matière peu conductrice telle que de la poudre de liège. Ainsi se trouve très atténuée toute possibilité d’action thermique tant par rayonnement que par conductibilité. L’isolement thermique devient encore beaucoup plus efficace si on peut faire et maintenir un très bon vide entre les deux enceintes métalliques, et c’est précisément ainsi que d’Arsonval en France, puis Dewar en Angleterre, ont réalisé ces récipients où de l’air liquide peut être conservé plusieurs jours, récipients qui, bien fermés, peuvent aussi servir pour conserver des liquides chauds (« bouteilles Thermos »). Plaçant au besoin l’un dans l’autre une suite de tels récipients, on arrivera à rendre aussi petite qu’on le voudra, pendant un temps fixé, l’action thermique extérieure.
7. Thermomètres et thermostats. — En opposition aux systèmes thermiquement isolés, se trouvent des systèmes sur lesquels une action thermique est facile, et qui ne connaissent l’extérieur que par action thermique (une enveloppe rigide pourra être nécessaire) tels les thermomètres et les thermostats.
Un thermomètre, dont le but est de déterminer rapidement à quel échelon de l’échelle des températures se trouve la température d’un objet donné, doit varier notablement quand sa température varie notablement, et reprendre exactement le même état aussitôt que cette température redevient la même, en sorte que cet état soit une fonction de la température ; cela permettra de « graduer » l’instrument une fois pour toutes.
On disposera ce thermomètre de façon que, par contact ou rayonnement, il puisse (sans subir aucune autre action thermique) être modifié par l’objet dont on veut repérer la température. (Objet qui sera par exemple de l’eau chaude où on plongera ce thermomètre). Et on attendra la mise en équilibre. Si cette mise en équilibre n’a fait varier que de façon insignifiante la température de cet objet, on aura repéré cette température par l’état alors pris par le thermomètre.
Un type usuel de thermomètre est constitué par une masse donnée de liquide (disons du mercure) qui emplit une petite ampoule de verre, dont une extrémité s’allonge en un tube capillaire gradué où s’arrête le niveau du liquide, en sorte qu’une petite variation de volume entraîne un grand déplacement du niveau. Un autre genre de thermomètre (thermomètre à gaz) repère la température par la variation de volume à pression constante, ou par la variation de pression à volume constant, d’une masse donnée d’un certain gaz. Un autre thermomètre bien différent repère la température de la soudure chaude d’un couple thermoélectrique (VIII, 46) dont la soudure froide est, disons, maintenue dans la glace fondante par la force électromotrice du couple. Et bien d’autres types de thermomètres ont été imaginés.
On gradue ordinairement les thermomètres selon une échelle « centigrade » marquant 0° dans la glace fondante, 100° dans l’eau bouillante, et disons 15° si la température a augmenté de façon que la variation du thermomètre soit 15 centièmes de ce qu’elle est pour l’intervalle (glace fondante — eau bouillante).
Un thermostat, dont le but est de pouvoir exercer des actions thermiques notables au moyen d’un objet de température fixée, et qui doit, comme le thermomètre, n’exercer (ou ne subir) que des influences thermiques, a pour propriété essentielle de ne pas changer de température pendant qu’il exerce (ou subit) ces influences, ou du moins de n’en pas changer assez pour que ces influences puissent en être modifiées appréciablement (ce qui nous permettra plus tard de considérer un thermostat comme une « source de chaleur à température constante »).
Un bon exemple de thermostat est donné par une glacière à la température de la glace fondante : toute influence thermique exercée ou subie s’y traduit en définitive par la fusion de glace ou la congélation d’eau.
Pratiquement on utilise souvent comme thermostat une grande masse d’eau, maintenue en équilibre thermique par agitation.
8. Enceintes isothermes. — L’espace intérieur à une enceinte de température uniforme, ou enceinte isotherme, a des propriétés remarquables. Supposons que le vide y soit fait. Ceci n’empêche pas qu’un objet quelconque, et en particulier un thermomètre, prend en tout point un état bien défini, tout à fait indépendant de la position de l’objet dans l’enceinte. Cette mise en équilibre thermique de l’objet témoin et de l’enceinte ne peut s’établir et se maintenir que par échange de radiations, et l’état d’équilibre atteint correspond à un état défini de radiation, le même en tout point intérieur à l’enceinte, quelle que soit la forme de cette enceinte et quelle que soit la nature de ses parois.
Nous rechercherons plus tard les caractères essentiels de cette radiation isotherme en équilibre.
CHANGEMENTS
9. La notion de changement. — En vue d’atteindre à la définition de l’énergie, je veux maintenant introduire l’importante notion de changement.
Si, pour les valeurs , d’une variable , une fonction de prend les valeurs , , l’accroissement de la fonction qui correspond à l’accroissement de la variable est défini sans qu’on ait rien à savoir sur les valeurs intermédiaires de la fonction dans l’intervalle .
De même, le « changement » d’un système qui a passé de l’état A à l’état B est entièrement défini par l’état initial A et l’état final B, sans qu’il y ait du tout à se préoccuper des états intermédiaires que le système peut avoir pris entre les états A et B. Ce passage est en général possible d’une infinité de manières, de même qu’il existe une infinité de chemins qui mènent d’un point à un autre, mais cela n’importe pas : c’est la différence brute entre l’état initial et l’état final qui définit le changement.
Par exemple le changement élévation de poids sera défini par la connaissance du niveau initial et du niveau final (toutes autres précisions pouvant être données sur l’état initial et l’état final), sans qu’on ait du tout à se préoccuper du chemin suivi entre ces deux niveaux.
De même, le changement subi par un gramme d’eau d’abord solide à la température de la glace fondante, puis liquide à la même température (toutes autres précisions pouvant être données s’il était nécessaire) est défini par là même, et sans qu’on ait à se préoccuper de savoir si on a fondu la glace sur un fourneau, ou par frottement, ou en la vaporisant puis en la condensant, ou de toute autre manière.
J’insiste sur ce qu’il s’agit de la différence brute globale entre l’état initial et l’état final. Si, par exemple, de l’eau d’abord liquide est devenue de la vapeur, nous ne chercherons pas à décomposer ce changement en fractions séparément relatives aux différentes propriétés de la substance telles que température ou densité, mais nous regarderons le changement comme un tout.
Toutefois, quand un système est décomposable en systèmes distincts (si par exemple il est formé de 3 grammes d’eau qui restent séparés dans leur transformation) nous aurons le droit de regarder le changement total comme formé de la « juxtaposition » des changements de ces systèmes partiels.
10. Changements identiques. Changements inverses. — Soient deux systèmes aussi différents que l’on veut, mais tels que pour chacun d’eux le changement consiste uniquement dans le fait que 1 gramme de glace est remplacé par 1 gramme d’eau liquide, tout le reste du système ayant repris son état initial ; nous regarderons comme identiques les changements des deux systèmes, Plus généralement, nous dirons que deux systèmes matériels ont subi le même changement si, à un même objet près qui a changé de même, le premier système n’a pas changé, non plus que le second.
De même qu’à tout vecteur on peut faire correspondre un vecteur opposé ayant pour origine l’extrémité du précédent et pour extrémité son origine, de même à tout changement correspondra un changement inverse , l’état initial de chacun des deux changements étant l’état final de l’autre. Ici encore, l’évolution particulière suivie entre l’état initial et l’état final n’intervient pas : le changement glace-eau est inverse du changement eau-glace quand même on aurait obtenu le premier par fusion et le second par évaporation puis liquéfaction de la valeur.
11. Changement d’un système donné. — Quand nous parlons du changement d’un système, nous n’entendons pas nécessairement que la matière s’y est conservée. Par exemple, nous pouvons parler du changement subi par une plante vivante qui aura cependant perdu ou gagné de la matière pendant le passage entre les deux états qui définissent ce changement. On peut même considérer des changements de systèmes non matériels : par exemple, si une enceinte vide de matière passe de la température de la glace fondante à celle de l’eau bouillante, le changement de la radiation contenue dans cette enceinte est défini.
Mais il sera souvent possible et commode de décomposer le système étudié en systèmes matériels qui auront pu rester « chimiquement isolés », c’est-à-dire qui auront pu rester assujettis à ne pas perdre et à ne pas gagner de matière. Aussi, à moins que le contraire ne soit spécifié, il sera entendu, quand nous parlerons d’un changement, que ce changement se rapporte à un même système matériel, qui ne perd ni ne gagne de matière, condition qu’on pourrait assurer en enfermant ce système dans un ballon scellé. Même si nous reprenons le cas d’une plante vivante, nous pourrions envisager un système chimiquement isolé constitué par la plante et par une certaine quantité de terre et d’air.
12. Changements efficients, définis comme ne pouvant apparaître ni disparaître sans répercussion. — Déjà nous avons cité des types de changement (abaissement ou élévation de poids et plus généralement travaux moteurs et résistants), dont nous avons compris qu’ils ne peuvent être produits isolément : par exemple il ne se peut pas, qu’un objet pesant, disons un ascenseur, d’abord à un certain niveau, soit retrouvé à un niveau différent, sans que quelque autre changement se soit produit en raison même de ce que cet objet pesant est abaissé ou élevé, ce changement corrélatif étant d’autant plus important que la variation de niveau est plus grande et que l’objet pèse davantage.
Ces caractères se retrouvent sur d’autres types de changements.
C’est ainsi que de l’eau, d’abord dans l’état de glace, ne peut pas devenir liquide sans qu’il se produise quelque autre changement corrélatif tel que abaissement de poids, ou refroidissement de quelque autre système matériel, ou disparition de radiation, etc…, changement corrélatif d’autant plus important qu’il s’est fondu plus de glace. Et réciproquement le changement inverse eau-glace se présente aussi toujours comme accompagné d’un changement corrélatif, tel que fusion de mercure, qui lui est proportionné en importance.
De même, il n’arrivera pas, sans changement conjugué, que de l’eau d’abord à une certaine température prenne une autre température, et plus généralement qu’un corps s’échauffe ou se refroidisse.
De même, la majeure partie des changements « chimiques » entraîneront des changements corrélatifs. Par exemple la formation de carbonate de chaux, à partir de chaux et de gaz carbonique, qui peut se produire sous un piston chargé de poids dans un thermostat à zinc bouillant en même temps que le poids s’abaisse et que du zinc s’évapore, ne se produira jamais isolément.
De même encore, il ne pourra jamais disparaître ou apparaître de radiation, de lumière, sans quelque changement corrélatif (par exemple échauffement du corps où la lumière disparaît).
Nous dirons de tous ces changements qui ne peuvent apparaître ni disparaître sans répercussion extérieure, proportionnée à leur importance, qu’ils sont efficients. L’observation seule nous révélera quels sont les divers types de changements efficients.
Nous dirons souvent, employant une abréviation expressive, qu’un changement achète, ou paie, un autre changement, quand il se produit sans autre répercussion extérieure. Et nous disons aussi bien que deux changements dont chacun forme l’unique répercussion de l’autre (qui sont donc payés l’un par l’autre) sont conjugués.
Nous discuterons bientôt les enchaînements par lesquels peuvent se conjuguer les changements efficients.
13. Changements isolables. — Deux changements efficients qui se conjuguent en épuisant leurs effets l’un par l’autre, forment, de ce fait, dans leur ensemble, un changement sans répercussion extérieure, ou, plus brièvement, un changement isolable. Est isolable par exemple tout changement constitué par l’élévation et l’abaissement de deux poids s’équilibrant sur un treuil. De même est isolable le changement à compensation interne constitué par l’arrêt d’un projectile et réchauffement qu’il produit par cet arrêt, s’il n’y a pas d’autre répercussion. Ou de même le changement global où un travail achète un échauffement (Rumford).
Mais un changement peut être isolable sans qu’on sache le décomposer en changements conjugués. Tel le changement qui se produit dans de l’eau surfondue et thermique, quand on y laisse tomber une paillette minuscule de glace.
On peut dire que tous les changements isolables sont gratuits, car ils ne coûtent (ni ne rapportent) rien.
Un exemple remarquable de changement isolable a été donné
par une expérience célèbre de Gay-Lussac, dite expérience de
Joule[3], réalisant la détente d’une masse gazeuse (disons d’air ou d’hydrogène) en ouvrant un robinet qui réunit, au sein d’un thermostat, deux récipients rigides, l’un plein de gaz et l’autre vide (fig. 1). 
Fig. 1. La masse gazeuse occupe bientôt, à
la température initiale, les deux récipients, et l’expérience montre qu’en
définitive le thermostat n’a pas subi
de changement. (Par exemple, s’il est
à glace fondante, la masse totale de
glace n’a pas varié) : le changement subi par une masse gazeuse
dont le volume a augmenté, (la température finale et la température
initiale étant les mêmes), ne coûte ni ne rapporte rien. (Cette
loi et la loi de Mariotte, définissent les « gaz parfaits »).
14. Changements non isolables mais dont l’inverse est isolable. — Une classe intéressante de changements contient tout changement qui peut, non pas se produire, mais disparaître sans répercussion. Tel est précisément le changement subi par une masse gazeuse, prise puis laissée à la même température, mais avec un volume diminué. Cette compression ne peut se produire « seule », mais une fois produite, elle peut disparaître par changement de Gay-Lussac sans répercussion extérieure.
De là résulte, évidemment, que tout changement conjugable avec une diminution de volume d’une masse gazeuse qui a gardé ou retrouvé sa température initiale est isolable, car il subsistera seul dès que la compression aura disparu par une détente isolable.
Le fait qu’une telle compression puisse disparaître sans répercussion, n’empêche pas qu’elle puisse présenter un intérêt pratique. Par exemple, une torpille se propulse dans l’eau, grâce à une réserve d’air comprimé qui fait tourner l’hélice en se détendant. Mais la répercussion de cette détente sera en définitive nulle (la torpille finira par s’arrêter, dans de l’eau qui, au total, ne sera ni échauffée, ni refroidie).
15. Changements indifférents. — Enfin certains changements sont strictement indifférents, pouvant aussi bien apparaître que disparaître sans répercussion. Tel est, par exemple, pour tout objet, le changement qui consiste en ce que son centre de gravité a changé de position, mais non de niveau. Tel est encore, au moins en première approximation, tout changement qui consiste en ce qu’une masse liquide n’a pas la même forme dans son état initial et son état final (changement qui finirait pourtant par avoir une répercussion si le liquide était subdivisé en gouttelettes de plus en plus petites, lui donnant une surface énorme.
ENCHAÎNEMENTS
ENTRE CHANGEMENTS EFFICIENTS
Nous voulons maintenant, généralisant ce que nous savons quant aux travaux moteurs et résistants, expliquer et comparer les enchaînements par lesquels peuvent se conjuguer, sans autre répercussion, des changements efficients.
16. Enchaînement d’un travail moteur avec un travail résistant. — Malgré que nous l’ayons déjà fait avec détail (IV, 11 à 15), nous voulons d’abord, dans cet esprit, rappeler le long effort par lequel les hommes ont fini par se convaincre qu’un poids ne peut s’élever « tout seul », ou, comme on a dit plus improprement, que le « mouvement perpétuel » est impossible.
Ayant compris que, par exemple, au moyen de poulies ou de treuils, nous pouvons acheter l’élévation du poids de la hauteur par l’abaissement d’un poids de la hauteur , sans autre répercussion, sous la condition que les produits et soient égaux (les deux changements se décomposant donc l’un et l’autre en autant de kilogrammètres), nous nous sommes demandé si quelque autre mécanisme, quelque autre genre d’enchaînement, permettrait de faire un marché plus avantageux, élevant par exemple en surplus un poids de la hauteur . En ce cas, nous pourrions toujours, par treuils ou poulies, remonter sans autre répercussion le poids de la hauteur , en abaissant de la hauteur le poids d’abord élevé, en sorte qu’il resterait, que le poids se serait élevé tout seul sans répercussion. Avec Galilée, nous avons jugé cela impossible et ainsi nous avons compris que :
Il y a équivalence entre tous les enchaînements qui achètent du travail résistant avec du travail moteur.
Nous allons élargir et généraliser ce principe, par étapes successives.
Et d’abord, discutons les enchaînements par lesquels l’arrêt ou le lancement d’un mobile se trouvent conjugués, soit avec un travail, soit avec le lancement ou l’arrêt d’un autre mobile.
17. Dévier un mobile exige un effort, mais ne coûte pas de travail. — Soit un point matériel en mouvement par rapport au sol.
Cherchons à changer sa vitesse. Des forces vont être nécessaires ;
mais l’opération n’est pas de même sorte selon que nous voulons
changer la direction de la vitesse ou changer sa grandeur. Dévier
un projectile ou l’arrêter sont choses bien différentes.
Considérons d’abord un point matériel en mouvement rectiligne et uniforme sur un plan horizontal fixé au sol et qui le soutient. Un moyen de changer la direction de cette vitesse, de « dévier » la course du mobile est de le saisir dans une position par un fil de longueur attaché à un point ou pivot fixé sur le plan, fil à ce moment rectiligne et perpendiculaire à la vitesse en et qu’enfin nous supposons pratiquement inextensible (fig. 2).
Sitôt le mobile saisi par ce fil, il ne peut continuer son mouvement rectiligne et décrit forcément, par rapport au sol, un cercle ayant pour centre, en même temps que le fil se tend, tirant ce mobile vers ce point , avec une force , normale au mouvement, qui laisse donc constante la vitesse . Mais, dès que nous supprimerons cette force[4] disons au point , le mouvement redeviendra rectiligne, tangent en au cercle abandonné ; la direction de la vitesse aura été déviée de l’angle .
Cette déviation a été produite sans que le fil tendu ait travaillé (le produit de la force par la variation nulle de la longueur du fil étant nul). La déviation du mobile a exigé qu’une force s’exerçât pendant un certain temps, qu’il y eût « effort » mais non pas travail, car elle n’a rien dépensé qui eût pu servir à élever un poids. Et nous pourrions indéfiniment recommencer l’opération ; nous ne sommes à cet égard ni appauvris, ni enrichis : la déviation est gratuite, en ce qui regarde la réserve dont nous pouvons disposer pour élever des poids.
J’observe qu’il est intéressant de définir un effort scalaire (relatif à la corde qui tire le mobile) aussi bien que l’effort vectoriel antérieurement défini (V, 16). Cet effort scalaire est la somme des grandeurs des efforts vectoriels élémentaires successifs.
Il est égal, ici, au produit de l’impulsion par la déviation. Soit cette élévation.
La force qui tire le mobile de masse vers le centre est (voir V, 8). D’autre part, l’arc décrit avec la vitesse constante est égal à . En sorte que :
Nous avons supposé la vitesse horizontale. Cette restriction peut être levée. Soit un point matériel qui va passer en dans la direction , avec une certaine vitesse (fig. 2). Sur , au delà de , menons par un point très voisin un axe arbitraire, le long duquel nous voulons dévier le mobile. Pour cela, réalisons un axe lié au sol, et perpendiculaire au plan , tel que sa trace sur le plan soit centre du cercle tangent à en , et à en un point . Soient et deux points fixes de cet axe, et supposons le mobile saisi, quand il passe en , par les deux cordons inextensibles et à ce moment rectilignes. Le mobile est alors forcé de décrire le cercle de rayon ; coupons les fils en , nous avons obtenu la déviation.
Nous l’avons obtenue « pour rien », car sur l’espace très petit les forces qui agissent sur le mobile n’ont pu effectuer de travail notable, et, d’autre part, si puissant qu’ait été « l’effort », nos cordons n’ont pas travaillé.
Il est d’ailleurs évident que la relation qu’on vient d’établir entre l’effort scalaire, la déviation, et l’impulsion, subsiste.
Bref, cela ne peut ni coûter ni rapporter de travail, de changer la direction d’un mobile en mouvement, de dévier un projectile. C’est un changement indifférent gratuit. Il n’en va pas de même s’il s’agit de ralentir ou d’accélérer le projectile.
18. Tout lancement de mobile coûte, et tout arrêt enrichit. — Comme pour ce qui regarde la production de travail, des observations familières en nombre immense ont imposé la conviction que, par rapport au sol, la mise en mouvement d’un mobile ou l’accroissement de sa vitesse ne se font jamais « tout seuls ». Il n’arrive jamais qu’un projectile soit lancé sans qu’il se soit produit par ailleurs quelque phénomène « moteur » (tel qu’un abaissement de poids, ou un ralentissement de quelque autre mobile, ou la détente d’un ressort, ou la combustion de la poudre d’une cartouche) qui, de façon évidente, selon tel ou tel enchaînement, a déterminé le lancement. Et, encore comme pour le travail, ce sera là une vraie dépense, proportionnelle au résultat, avec un changement extérieur qui nous laisse appauvris puisque nous aurons par exemple, ensuite, moins de poudre disponible, et que notre capital en possibilités de lancement sera diminué.
Symétriquement, il n’arrive jamais que, par rapport au sol, la vitesse d’un mobile diminue sans qu’il se passe quelque part une répercussion, d’autant plus importante que le mobile est plus massif et plus rapide. Un projectile déterminera par exemple, en s’arrêtant, des travaux résistants ou des échauffements.
Nous sommes, en particulier, assurés qu’une déviation de projectile dont nous venons de voir qu’on l’obtient gratuitement, laisse la vitesse inchangée.
19. Enchaînement de lancement ou d’arrêt avec travail. — Un travail moteur, qui peut « acheter » (12) un travail résistant, peut aussi bien acheter un lancement de mobile. De même, l’arrêt du mobile peut acheter un travail résistant ou lancer un autre mobile. Travail moteur et arrêt de mobile sont deux phénomènes moteurs ; travail résistant ou lancement de mobile sont deux phénomènes résistants.
Le treuil permet de réaliser ces quatre genres d’enchaînements.
Nous savons déjà comment il permet de conjuguer (12) un
travail moteur avec un travail
résistant (enchaînement ).
il permet de conjuguer (12) un
travail moteur avec un travail
résistant (enchaînement ).
Nous pouvons maintenant imaginer (fig. 3) qu’un poids , suspendu par un fil enroulé sur la gorge de la petite poulie, entraîne horizontalement le chariot ou traîneau , par l’intermédiaire d’un fil passé sur la grande poulie, lançant ainsi progressivement ce chariot avec une vitesse qui sera devenue quand le poids sera descendu de (enchaînement ). Le rapport des rayons des poulies aura été pris assez grand pour que, même à ce moment, le mouvement de descente du poids soit très lent, et que ce poids soit presque en équilibre, le travail qu’il a fourni étant .
Réciproquement, le chariot lancé en sens inverse remonterait le poids, le laissant à chaque instant presque en équilibre (enchaînement c).
Enfin, le chariot ayant, en s’arrêtant, remonté de le poids , nous pouvons décrocher ce chariot, le laissant en repos, puis accrocher un autre chariot sur une autre poulie du treuil (généralisé) ; redescendra de et sera dans son état initial, et il reste en définitive à ce moment un deuxième chariot lancé par suite de l’arrêt d’un premier (enchaînement ). Cet enchaînement , formé d’abord d’un enchaînement [travail produit par l’arrêt du premier mobile, puis d’un enchaînement (lancement du second mobile par dépense de ce travail)] n’est ici pas direct. Mais on peut réaliser des enchaînements directs d’espèce .
Étendant la notion de treuil, imaginons en effet au lieu de deux poulies circulaires solidarisées sur un même axe, deux poulies coniques solidarisées sur cet axe, chacune à gorge spiralée courant de la base au sommet du cône formant la poulie conique. Le système qu’on veut ralentir sollicite par un fil ce treuil spiralé, tirant sur l’un des cônes près de la base où le rayon est grand ;
celui qu’on veut lancer est tiré par un fil tirant en sens inverse
sur la gorge de l’autre cône, dans la région, proche du sommet,
où les spires sont petites ; il peut ainsi partir avec une vitesse
faible, qui grandira progressivement à mesure que son fil d’attache
se rapprochera de la base du cône ; au contraire, le chariot moteur,
dont le fil s’approche du sommet du cône, pourra, même si sa
vitesse tend vers zéro, accroître encore la vitesse, devenue grande,
du second chariot. Il est manifeste qu’on pourra s’arranger, avec
gorges spirales convenables, pour que la traction due au chariot
qui se ralentit garde, par rapport à l’axe, un moment toujours
un peu supérieur à la traction exercée par le chariot qui s’accélère
(fig. 4).
Ainsi divers mécanismes peuvent réaliser les quatre genres d’enchaînements entre les phénomènes moteurs « travail moteur » et « arrêt de mobile » et les phénomènes résistant « travail résistant » et « lancement de mobile ». Le schéma ci-contre (fig. 5), qui sera généralisé, indique, par le moyen de flèches allant du phénomène « cause » au phénomène « effet », le sens et la possibilité de ces enchaînements. Nous allons montrer que les mécanismes qui peuvent les produire sont tous équivalents.
Nous allons, pour cela, suivant l’ordre historique du développement des idées, faire intervenir des abaissements ou élévations de poids en « chute libre » ou « ascension libre », mais nous devons d’abord expliciter une propriété remarquable de la pesanteur, au fond déjà admise dans les énoncés qui précèdent.
20. Le poids d’un corps ne dépend pas de sa vitesse. — Considérons la force que développe le vent sur un bateau qu’il pousse par l’arrière. Le travail de cette force entre deux positions de ce bateau, et la force elle-même, ne sont pas les mêmes si le bateau avance très lentement (la poussée exercée par le vent restant alors constante) ou s’il avance de plus en plus rapidement (la poussée exercée par le vent diminuant alors, jusqu’à s’annuler si la vitesse du bateau devient égale à celle du vent). De même il se pourrait que le poids d’un corps diminuât, quand ce corps tombe dans la direction de la pesanteur, ce poids étant une fonction décroissante de la vitesse verticale. Alors que le travail de la pesanteur sur un corps, ayant en équilibre le poids , et qui descend très lentement de la hauteur est , il serait inférieur, et de la forme quand le corps tombe en chute libre.
C’est ce qui n’a pas lieu ; laissons tomber le corps en chute libre de cette hauteur et prendre ainsi une vitesse . Dévions-le alors sans changer son niveau (ceci ne coûte rien), en sorte qu’il coure avec cette vitesse sur un plan horizontal, et accrochons-le alors à un fil tendu sur la poulie extérieure d’un treuil (fig. 5) dont un poids sollicite en sens inverse la poulie intérieure, en sorte que l’ascension de soit aussi lente qu’on le veut, même quand le mobile a sa plus grande vitesse. Bientôt ce mobile s’arrêtera, ayant remonté de un poids qui est pratiquement resté toujours en équilibre. Fixons à cet instant ce mobile par une clavette. Aucun changement ne se trouve alors réalisé, hors que , de nouveau en équilibre, est descendu de et que , aussi en équilibre, a remonté de .
Si le travail fourni pendant la chute, et qui, selon le principe de Galilée, doit se retrouver dans l’élévation de était inférieur à , le travail égal serait aussi inférieur à Et, remontant par une machine simple fonctionnant sans vitesse ce que nous pourrions du poids à son niveau primitif, il nous resterait qu’une certaine partie de ce poids se trouverait abaissée, sans effet extérieur produit. En regardant cela comme impossible, nous avons donc implicitement admis que le poids d’un corps en mouvement est égal au poids du corps en repos.
Un raisonnement analogue s’appliquerait aux forces électriques ; elles ne dépendent pas de la vitesse du corps chargé.
21. Équivalence des enchaînements entre lancements ou arrêts et travaux. — Maintenant nous pouvons établir l’équivalence des mécanismes qui enchaînent travaux et variations de vitesse.
Une façon de lancer un objet par abaissement d’un poids (flèche ) est simplement de laisser tomber cet objet en « chute libre ». La pesanteur agit alors seule, et, pour la hauteur de chute , qui donne au mobile une vitesse , dépense un travail . Au prix de ce travail, nous ne pourrons faire ni mieux, ni plus mal.
Nous savons, en effet (treuil de la figure 3), que nous pourrons alors, en arrêtant le corps lancé, soulever un poids égal d’une hauteur , retrouvant le travail , dépensé pendant la descente. Si, par un autre mécanisme que la chute libre, nous avions obtenu une vitesse supérieure pour la même dépense initiale , nous pourrions, déviant le corps lancé sur un plan horizontal et l’attachant à la poulie extérieure de notre treuil, lui faire remonter plus haut le poids égal soulevé par le treuil et avoir en définitive « pour rien » une élévation de poids. Et si notre mécanisme était moins avantageux que la chute libre, c’est un abaissement « perdu », sans effet, qui nous resterait comme seul changement.
Considérons maintenant l’enchaînement où l’arrêt d’un mobile effectue un travail résistant, par exemple élève un poids. Ce mobile eût pu prendre sa vitesse en chute libre de hauteur , sous l’action de son poids . Cela dit, si (après qu’on l’a dévié, de façon que son mouvement, renversé, se dirige vers le haut) il perd sa vitesse par ascension libre (transformation ), il est forcément monté de , sans quoi nous aurions, à partir de son état de repos, un poids monté tout seul ou descendu sans effet. Et il n’arrivera pas qu’un mécanisme autre que l’ascension libre, en arrêtant le mobile lancé à la vitesse , élève de la hauteur ; sans quoi, laissant retomber de , nous retrouverions le mobile lancé à la vitesse avec un travail obtenu pour rien. (Démonstration analogue, si notre mécanisme était supposé moins avantageux que l’enchaînement par ascension libre).
Enfin, nous savons lancer un second mobile par arrêt d’un premier (enchaînement ). Supposons cela fait par deux mécanismes différents. Arrêtons le second mobile en lui faisant remonter un poids. Tout se réduit alors à ce que le premier mobile est arrêté et le poids remonté (enchaînement ) ; cette élévation de poids a donc une valeur fixée ; tandis qu’elle prendrait deux valeurs différentes si nos mécanismes n’étaient pas également avantageux.
Bref, le principe d’équivalence de Galilée se trouve étendu aux lancements ou arrêts de mobiles.
Nous allons en obtenir des généralisations d’autres sortes.
22. Changements thermiques. — Nous avons acquis la notion de température en partant de ce que deux corps peuvent se modifier réciproquement par conductibilité ou rayonnement.
Nous appellerons « changements thermiques » les changements qui peuvent être ainsi produits en conséquence de différences de température, sans intervention d’aucune autre action, et avec retour possible à l’état initial si la température primitive est restaurée (ceci excluant les actions photochimiques, ou les travaux produits par pression de radiation). Tel le changement efficient « congélation d’eau » que peut payer, par mise en contact, le changement « fusion de mercure solide ». Tel le changement « fusion de glace » qui peut être produit en mettant la glace sur un fourneau (conductibilité) ou en l’exposant devant un feu ardent (rayonnement). Tel encore le changement de 1 gramme d’eau pris à la température de 15° et laissé à celle de 16°. Ce dernier changement, qu’on utilise commodément en des enchaînements de changements thermiques, définit la calorie.
On ne manquera pas de remarquer que les changements thermiques produits dans un objet froid par action d’un objet chaud peuvent être achetés, au moyen de frottements, par du travail moteur ; mais, même alors, le changement se produit en conséquence d’élévations de température (faibles et transitoires, mais inévitables) dues au frottement. Et le changement considéré se produit en définitive toujours par voie thermique.
Les changements thermiques peuvent être conjugués avec une apparition ou une disparition de Lumière (45) : par exemple, de la lumière jaune absorbée par un système qu’elle échauffe peut toujours être regardée comme provenant, au travers d’un écran sélecteur qui n’en laisserait pas sortir d’autre, d’un objet à température suffisamment élevée, qui par là se refroidit.
Comme pour l’élévation ou l’abaissement d’un poids, comme pour le lancement ou l’arrêt d’un mobile, des observations familières en nombre immense ont imposé la conviction que les changements thermiques ne peuvent se produire « seuls », ne peuvent constituer des changements isolés. Et, comme pour les travaux, ou comme pour les mobiles dont la vitesse change, nous pouvons distinguer des changements thermiques « moteurs » et des changements thermiques « résistants ».
Sont « résistants » ou « positifs » à la façon d’un lancement de projectile, ou d’une élévation de poids et plus généralement d’un travail résistant, les changements thermiques produits au prix d’un phénomène « moteur » (tel que l’abaissement d’un poids, ou la détente d’un ressort, ou l’arrêt d’un projectile). Ces changements thermiques « résistants » ou « positifs », (échauffements, fusions, émissions de lumière, etc.) peuvent toujours être produits par action thermique d’un corps « chaud », qui alors se refroidit.
Symétriquement sont « moteurs » ou « négatifs » les changements thermiques (refroidissements, congélations, absorptions de radiation, etc.) qui enrichissent l’extérieur comme peut faire un abaissement de poids, étant capables, par exemple, de déterminer l’échauffement d’un corps « froid ».
23. Équivalence des enchaînements entre changements thermiques. — Un changement thermique a été défini comme pouvant être la cause ou l’effet d’un autre changement thermique, rien d’autre ne se passant. Par exemple la fusion de glace peut être achetée par le refroidissement d’une masse de mercure qui passe de la température de l’eau bouillante à celle de la glace fondante, sans autre répercussion.
Faisant cette expérience, en versant directement le mercure chaud dans la glace fondante, nous trouverons, par kilogramme de mercure, 42 grammes de glace fondue. Pouvons-nous, au prix du même refroidissement, mais en nous y prenant autrement, réussir un « marché » plus avantageux, par exemple fondre 50 grammes de glace ?
Nous ne pouvons plus répéter ici le raisonnement par lequel nous avions répondu à une question semblable (IV, 14) au sujet de l’élévation d’un poids par l’abaissement d’un autre poids. Nous ne pouvons plus dire que nous n’avons qu’à renverser le premier enchaînement pour réchauffer notre kilogramme de mercure en recongelant 42 grammes de glace, après quoi il nous resterait 8 grammes de glace fondue « gratuitement », ce que nous regardons comme impossible. Nous ne pouvons plus le dire parce que nous ne savons pas renverser l’enchaînement « fusion de glace par refroidissement d’un corps plus chaud » (et bientôt nous reconnaîtrons qu’il y a là une impossibilité essentielle).
Nous affirmerons cependant, après bien des essais, qu’il n’est pas possible, en un changement isolé qui se réduise au refroidissement de un kilogramme de mercure et à de la fusion de glace, de trouver jamais plus (ni moins) que 42 grammes de glace fondue. Plus généralement, l’expérience a toujours donné une équivalence exacte entre les divers procédés par lesquels on sait enchaîner deux changements thermiques.
24. Calorimètre. — C’est la validité générale de cette équivalence qui a rendu possible la « calorimétrie », c’est-à-dire la mesure des changements thermiques (ou, comme on dit souvent pour des raisons que nous donnerons, la mesure des « quantités de chaleur »), dans les opérations où interviennent seulement des actions thermiques.
Un changement thermique « résistant », « positif », aura pour mesure le nombre s’il « vaut » fois un certain changement thermique positif choisi comme unité (on choisit généralement la calorie), c’est-à-dire s’il peut être payé par un changement thermique qui pourrait aussi bien payer le changement thermique constitué par fois le changement unité (soit calories).
On voit que la somme des valeurs de deux changements thermiques payés l’un par l’autre est nulle.
La notion de changement thermique, fixée avec l’état initial
et l’état final, ou, si on préfère, celle de quantité de chaleur
perdue ou gagnée entre ces deux états, n’a été clairement dégagée
qu’au XVIIIe siècle, notamment grâce
au physicien anglais Black.

La mesure se fait au moyen d’un calorimètre, système matériel assujetti, comme un thermomètre ou un thermostat, à ne connaître l’extérieur que par action thermique. Ce sera, par exemple, un calorimètre à eau (fig. 6) constitué par une masse connue d’eau contenue dans un vase métallique mince soutenu par des supports isolants au sein d’une enceinte métallique protectrice à double paroi, emplie d’eau sensiblement à la même température.
Soit à déterminer, au voisinage de la température ordinaire, la chaleur spécifique du métal dont est fait le vase calorimétrique (disons, du cuivre). C’est-à-dire soit à trouver la valeur du changement thermique subi par 1 gramme de ce métal quand sa température varie de 1° au voisinage de 15°. Soit la température initiale. Nous trouverons que grammes de ce métal à la température , immergés dans le calorimètre, l’amènent à la température , une fois l’équilibre établi. Le changement thermique de la masse immergée est alors , celui de l’eau est et celui du vase est . Donc, écrivant que la somme des deux changements thermiques payés l’un par l’autre est nulle, on a :
ce qui donnera , soit 0,1 calorie dans le cas du cuivre.
Il est essentiel de comprendre que nous trouverons toujours même valeur pour , de quelque façon que soit conduite l’expérience.
Après quoi, désignant par la somme désormais connue, appelée souvent « valeur en eau du calorimètre », nous aurons toute autre chaleur spécifique par une équation de même sorte :
Nous mesurerons de même, par exemple, le changement thermique « fusion de 1 gramme de glace à la température 0° de la glace fondante » ou « chaleur latente de fusion de la glace », de valeur , selon une équation :
trouvant ainsi pour , quelle qu’ait été la façon de procéder, 80
calories.
Et ainsi de suite.
Il va de soi que nous pourrons changer le liquide calorimétrique et le vase qui le contient. (Nous aurons notamment avantage à prendre pour vase calorimétrique un vase d’Arsonval-Dewar). Nous déterminerons la « valeur en eau » du nouveau calorimètre, par exemple en y versant une masse d’eau à une température et mesurant la température une fois l’équilibre réalisé, d’où l’équation :
Nous pourrons substituer au calorimètre à eau un calorimètre à glace fondante, (mesurant le poids de glace fondue quand on y introduit l’objet dont on mesure le changement thermique) ou employer tout autre genre de calorimètre. Dans tous les cas, quels que soient les intermédiaires entre l’état initial et l’état final, la mesure d’un même changement thermique, disons la fusion de 1 gramme de glace à 0°, donne le même résultat.
Au XVIIIe siècle, on interprétait cette concordance en admettant l’existence d’un fluide calorifique indestructible ou « chaleur » qui abandonnait le corps refroidi pour entrer dans le corps échauffé. L’équation calorimétrique exprimait que la chaleur perdue par un corps était gagnée par l’autre, en sorte qu’il y eût « conservation du calorique ». Ce postulat fut abandonné quand on s’avisa que le frottement peut « créer » du calorique, mais il reste que la cohérence des résultats de la calorimétrie établit pour les changements thermiques un principe d’équivalence analogue à celui que nous avons énoncé pour les changements mécaniques, c’est-à-dire que :
Aucun dispositif n’est plus avantageux qu’un autre pour « acheter » un changement thermique d’une sorte donnée (disons fusion de glace) avec un changement thermique d’une autre sorte donnée (disons refroidissement de cuivre).
Nous comprendrons au surplus bientôt, quand nous aurons dégagé la notion d’énergie, qu’il n’était aucunement incorrect de parler de quantité de chaleur ou de déplacement de chaleur, à la condition de ne pas considérer cette chaleur comme indestructible en tant que chaleur.
24. Thermochimie. — Considérons une réaction chimique accomplie sans travail, dont la répercussion extérieure se réduit à un changement thermique. Par exemple considérons le système matériel constitué par : 1,7 gr. de gaz ammoniac, 3,65 gr. de gaz chlorhydrique, et 100 grammes d’eau liquide, chacune de ces matières étant prise à 0° sous la pression atmosphérique (état initial). Nous pouvons de bien des manières transformer ce système en une solution aqueuse de sel ammoniac à 0° sous la pression atmosphérique (état final), par exemple en laissant les deux gaz se mélanger puis le sel ammoniac se dissoudre, ou en laissant dissoudre le gaz chlorhydrique dans la moitié de notre eau, le gaz ammoniac dans l’autre moitié et en mélangeant les deux solutions.
Si cependant on a veillé, comme il est ici facile, à ce que toute répercussion extérieure se réduise à des changements thermiques, en définitive toujours réductibles à la production de calories, nous trouverons que par tous les moyens employés, nous obtenons le même nombre de calories. Ici encore il n’est pas possible, au prix d’un même changement chimique et sans autre répercussion extérieure, d’obtenir par un moyen la fusion de dix grammes de glace et par un autre moyen plus avantageux la fusion, disons, de douze grammes de glace. De nouveau nous voyons que la Nature vend à prix fixe. Dans le langage utilisant l’hypothèse du calorique, on disait que la « quantité de chaleur » dégagée dans une réaction, où l’état initial et l’état final sont donnés, est déterminée. C’est ce qui a été clairement compris, et énoncé comme « principe de l’état initial et de l’état final », au xix siècle par le chimiste français Berthelot, et depuis appliqué dans les innombrables mesures thermochimiques exécutées par Berthelot en France, Thomsen en Allemagne, et par leurs continuateurs.
Considérons des réactions dont l’état initial et l’état final sont tels que la répercussion puisse en être entièrement thermique, comme il arrive pour les réactions produites dans un récipient rigide (« bombe calorimétrique » de Berthelot), qui sera plongé dans un calorimètre. Ces réactions seront dites exothermiques si le changement thermique extérieur correspondant est positif, endothermiques s’il est négatif.
26. Enchaînement, par frottement, d’un travail avec un changement thermique. — Les frottements vont enfin nous permettre de lier changements thermiques et mécaniques et d’atteindre en sa forme générale la notion d’équivalence des changements.
Nous avons indiqué déjà comment l’observation journalière donne l’exemple de travaux produisant des échauffements par frottement. Rumford, dès le xviiie siècle, comme nous l’avons alors rappelé (1), avait ainsi amené à l’ébullition l’eau d’une grande cuve, par frottement, au sein de cette cuve, contre une pièce métallique immobile, d’une autre pièce maintenue en rotation par un manège que faisaient tourner des chevaux. Et cette expérience où se créait du « calorique », sans qu’aucune matière fût transformée, par suite sans qu’aucune matière eût pu en perdre, fut justement opposée à l’hypothèse de la conservation du calorique.
Il y avait dès lors peu à faire pour introduire la mesure en de telles expériences. Peu à faire sinon précisément de comprendre l’intérêt immense de cette mesure. Il fallut attendre pour cela Joule (1845), dont l’expérience fondamentale (qui au fond n’est qu’une modification de l’expérience de Rumford) peut être résumée comme il suit :
Deux poids, en s’abaissant, font tourner, par l’intermédiaire
de poulies et de cordons enroulés en des sens concordants, un
tambour (fig. 7) qui entraîne, au moyen d’un axe vertical, un
agitateur à palettes dans un calorimètre plein d’un liquide quelconque
et thermiquement bien isolé. D’autres palettes, fixées à la paroi du vase, rendent très grand le frottement produit dans le
liquide par la rotation de l’agitateur, en sorte que les poids
prennent bientôt une vitesse limite uniforme et, après avoir descendu
de quelques mètres, atteignent leur niveau inférieur avec
cette vitesse qui est très faible. La température du système calorimétrique
aura alors monté, et notre connaissance des chaleurs spécifiques permettra de savoir combien
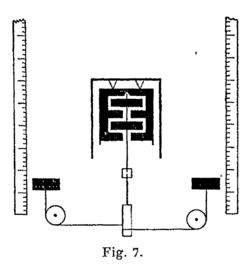
de calories il fournirait en revenant par refroidissement à son état initial. Ces calories sont achetées par l’abaissement des poids qui, pratiquement[5] n’a pas d’autre répercussion. Le changement global constitué par l’abaissement du poids et par l’échauffement du calorimètre de Joule est donc, par définition, « isolable ». De façon générale, nous
appellerons « changement de Joule » tout changement isolable
où un travail et un changement thermique se conjuguent, c’est-à-dire
épuisent exactement leurs effets l’un par l’autre.
27. Équivalence des enchaînements entre changements mécaniques et thermiques. — On trouve dans l’expérience de Joule que chaque kilogramme abaissé de 1 mètre engendre environ 2,33 calories, ou, si on préfère, qu’il faut 428 kilogrammètres pour échauffer 1 kilogramme d’eau de 1°, c’est-à-dire pour engendrer 1000 calories. Ou encore, en nous rappelant (V, 7) que 1 erg est le travail accompli par 1 dyne déplaçant son point d’application de 1 centimètre, qu’il faut ergs pour engendrer 1 calorie. Ceci, en changeant de toute façon imaginable les conditions de l’expérience. Par exemple, on retrouve ce résultat en forçant de l’eau à filtrer au travers d’un piston poreux chargé de poids, qui s’abaisse lentement pendant que l’eau s’échauffe par le fait de ce frottement, et sans que rien d’autre se produise.
Bref, quel que soit le genre de l’enchaînement entre un changement mécanique et un changement thermique, on retrouve toujours prix égal pour résultat égal : il y a équivalence des enchaînements possibles, comme entre changements mécaniques et comme entre changements thermiques, ou encore :
Aucun dispositif n’est plus avantageux qu’un autre pour acheter de la chaleur avec du travail.
C’est cela qui permet de parler de l’« équivalent mécanique de la calorie » (ou de l’équivalent thermique du kilogrammètre).
28. Premier principe de la thermodynamique. — Au point où il vient de parvenir, le lecteur n’aura qu’à se rappeler les principes partiels successivement atteints sur l’équivalence des enchaînements — entre travaux moteurs ou arrêts de mobiles avec travaux résistants ou lancements de mobile, — entre changements thermiques ou chimiques avec changements thermiques, — et, enfin, comme on vient de voir, entre travaux moteurs (ou arrêts de mobiles) avec changements thermiques, — pour ne pas hésiter sur la généralisation à tous changements efficients.
Nous allons ainsi admettre, sans en donner d’autres raisons, et sauf désaccord avec l’expérience, qui ne s’est jamais produit, le Principe général d’Équivalence des mécanismes d’enchaînement entre changements efficients, que nous énoncerons comme il suit :
Si deux changements efficients peuvent être conjugués au moyen d’un certain dispositif, il est impossible de réaliser un autre dispositif plus avantageux ou moins avantageux qui conjuguerait avec un de ces changements d’abord l’autre, et, en surplus, un autre changement efficient, positif ou négatif.
Il reste d’ailleurs possible qu’un autre dispositif enchaîne, avec le changement isolable constitué par les changements efficients que le premier dispositif conjuguait, un autre changement par ailleurs isolable, tel qu’un changement de Joule : cela ne réalise aucun bénéfice par rapport au premier dispositif.
Il n’est pas non plus en opposition avec notre Principe qu’un
autre dispositif puisse conjuguer, avec le changement isolable
constitué par les deux changements efficients conjugués par le
premier dispositif, un changement instable (14) qui peut disparaître
sans répercussion. Par exemple, au lieu de conjuguer par
frottement, comme dans l’expérience de Joule, un abaissement
de poids avec une fusion de glace, on peut les conjuguer en comprimant sous un piston de plus en plus chargé, une masse gazeuse dans un corps de pompe 
Fig. 8.
plongé dans un thermostat à glace fondante (fig. 9).
La glace fond en même proportion que
dans l’expérience de Joule, mais, en
outre, le volume du gaz est réduit. Ce
dernier changement peut disparaître
sans répercussion, par détente de Gay-Lussac
(13), ou avec une répercussion
pouvant elle-même disparaître sans répercussion
(14). En aucun cas, il n’est
obtenu de bénéfice ou perte sous forme de changement efficient
positif ou négatif.
Le Principe d’Équivalence va nous permettre d’acquérir la
notion d’Énergie. Mais d’abord nous devons comprendre comment,
en conséquence de ce Principe, les changements efficients peuvent
être tous mesurés, en définitive parce que, de proche en proche,
un changement efficient de n’importe quelle sorte peut soit acheter,
soit remplacer un changement de n’importe quelle autre sorte.
LA NOTION D’ÉNERGIE
29. Mesure commune aux changements mécaniques ou thermiques. Changements thermodynamiques. — Déjà nous savons que tout changement mécanique « moteur » (travail moteur, ou arrêt de mobile) peut avoir comme répercussion unique la production de calories, disons calories. Nous savons, d’autre part, qu’il peut aussi bien avoir comme répercussion unique un travail résistant qui, acheté au même prix, a donc même « valeur » que calories. Or, ces calories pourraient être produites par un refroidissement (valant donc calories) aussi bien que par notre travail moteur qui vaut donc aussi calories. On voit ainsi que tout changement mécanique ou thermique s’exprime, se mesure, par un nombre défini de calories, positif ou négatif. Il est manifeste, du même coup, que ce changement peut aussi bien se mesurer en ergs, en nous rappelant que 1 calorie peut s’acheter par le même travail moteur que le travail résistant ergs, c’est-à-dire vaut ergs.
Bref, nous pouvons mesurer, au moyen d’un « changement unité » mécanique ou thermique arbitrairement choisi, les changements mécaniques, les changements thermiques, et plus généralement tout changement thermodynamique constitué par un ensemble de changements mécaniques et thermiques. En particulier, un « changement de Joule » (décomposable en un travail moteur et un échauffement dont chacun est l’unique répercussion de l’autre) a la valeur zéro.
Plus généralement, tous changements qui peuvent apparaître ou disparaître sans répercussion (13 et 14), ne valant rien comme possibilité de travail ou d’ailleurs de tout changement efficient,
ne pourront avoir que cette valeur zéro.30. Figuration des enchaînements. — Nous pouvons exprimer par une figuration utile, et qui sera généralisable à tout enchaînement, les possibilités d’enchaînements thermodynamiques.
Nous avons vu comment l’expérience de Joule conjugue un travail moteur (ou selon une extension évidente un arrêt de projectile) avec un échauffement. Mais nous n’avons pas donné, et (ce sera le principe de Carnot) nous ne pourrons pas donner d’exemple d’un travail résistant payé par un refroidissement.
Nous reprendrons, pour exprimer les possibilités d’enchaînement thermodynamique, le genre de figuration plus haut indiquée (19, fig. 6) où des flèches allant du phénomène moteur à celui du phénomène résistant indiquent la possibilité et le sens des enchaînements dont nous avons vu qu’ils peuvent se produire « spontanément » (après « déclic ») (fig. 10).
Une flèche manque, qui indiquerait la possibilité d’achat d’un travail résistant par un refroidissement. Nous avons enfin figuré en ponctué la flèche qui marque la possibilité d’un échauffement (d’un corps « froid ») par refroidissement (d’un corps « chaud ») précisément pour rappeler que (alors que tout échauffement peut être produit par abaissement d’un poids) tout échauffement ne peut pas être produit par n’importe quel genre de refroidissement : on ne fond pas du fer en congelant de l’eau, malgré que les signes de ces deux changements soient du sens voulu (et ceci encore ressortira du principe de Carnot).
Plus généralement, un changement thermodynamique pourra être acheté par un ensemble de deux des changements types indiqués dans la figuration. Par exemple, le changement par transformation de vapeur d’eau saturante en eau liquide à 0° pouvant s’effectuer dans un corps de pompe sous un piston (chargé d’un poids exerçant une pression très légèrement supérieure à la pression de saturation) (le tout étant placé dans un thermostat à glace fondante), sera acheté par le changement complexe abaissement de poids (travail moteur) plus fusion de glace (type échauffement). Le nombre mesurant cette liquéfaction sera, en calories, la somme algébrique de ceux qui mesurent cet abaissement et cette fusion.
31. Tout changement efficient peut être payé par un changement thermodynamique. — Au point où nous sommes parvenus, nous comprenons que l’on peut mesurer par un nombre de calories ou d’ergs, tout changement efficient réalisé dans un système qui ne connaît l’extérieur que par voie mécanique ou thermique. On trouvera sans doute que ceci est bien général si on réfléchit par exemple que tel est le cas pour un homme qui voit, entend et touche. Pour la vue et la radiation thermique, l’extérieur serait alors remplaçable par des thermostats (éventuellement munis d’écrans sélecteurs de radiations et de lentilles convenables, en nombre immense, peu importe) ; pour l’oreille et le toucher (actions mécaniques), l’extérieur serait équivalent à un nombre immense de fils tendus. Il est au reste évident que par exemple il est hors de notre pouvoir de réaliser, en un système variable d’instant en instant les cordons délicats qui remplaceraient pour l’oreille l’action variable qui nous permet, disons d’écouter un concert. Mais la substitution est rationnellement possible et cela nous suffit.
Si pourtant l’homme que nous considérons use du téléphone, le système qu’il forme avec cet appareil ne paraît plus uniquement sollicité par des actions mécaniques et thermiques, et il y faut ajouter les actions qui s’exercent par les bornes où est branché l’appareil. Mais nous comprendrons bientôt (IX, Électrodynamique) que ces bornes pourraient à chaque instant être les pôles de dynamos plongées dans des thermostats et sollicitées par des poids moteurs, dynamos qui, en définitive ne subissent aucun changement, et fonctionnent comme un mécanisme de transmission. Bref, dans ce groupe de cas encore, l’influence exercée par le monde extérieur sur le système considéré pourrait s’exercer par fils tendus et thermostats. En sorte que, décidément :
Tout changement peut se payer en monnaie thermodynamique.
Le système poids et thermostats qui peut à chaque instant remplacer l’extérieur peut d’ailleurs être grandement simplifié.
Considérons d’une part les poids, qui, du point de vue mécanique peuvent remplacer l’extérieur. Nous pouvons ramener chacun de ces poids à son niveau initial par abaissement ou élévation d’un poids auxiliaire unique agissant par treuils ou poulies sur le poids particulier envisagé. De sorte qu’en définitive tout le travail extérieur aura été absorbé ou fourni par le poids auxiliaire.
Considérons d’autre part un thermostat auxiliaire de température plus froid que chacun de ceux auxquels le système a fait subir par action thermique un changement positif (« échauffement »). Par simple contact, ce thermostat auxiliaire pourra ramener chacun de ces thermostats dans son état initial, subissant lui-même au total un échauffement égal à la somme des actions thermiques extérieures positives du système.
De même, on pourra ramener dans son état initial chacun des thermostats extérieurs qui auraient subi un changement négatif (« refroidissement »), en refroidissant à leur contact un même second thermostat auxiliaire de température plus chaud que chacun d’eux, et qui subira le refroidissement .
Ainsi le changement efficient le plus général peut être payé :
par le travail d’un poids unique, mesurant l’action mécanique extérieure ;
par l’échauffement d’un thermostat auxiliaire et le refroidissement d’un autre thermostat auxiliaire mesurant à eux deux l’action thermique extérieure.
Simplifiant encore, et que notre poids auxiliaire unique ait monté ou descendu, nous pourrons toujours en une expérience de Joule laisser ce poids descendre assez pour restituer dans son état primitif celui des deux thermostats auxiliaires qui aurait été « refroidi ».
Tout se réduirait alors, comme répercussion extérieure conjuguée avec notre changement, au travail d’un poids unique abaissé ou élevé et à l’échauffement d’un thermostat unique. Bien entendu, n’est pas forcément égal au travail extérieur , ni à l’action thermique extérieure . Mais la somme égale à mesure aussi bien la répercussion extérieure du changement. Bref :
Tout changement peut se payer par une variation de niveau d’un poids, et par un échauffement d’un thermostat.
32. Mesure thermodynamique d’un changement. — Ainsi nous pouvons regarder comme résolue la question que nous nous étions posée : chaque changement efficient peut être payé par un travail (moteur ou résistant) et un échauffement de thermostat. La somme changée de signe (en sorte que le changement isolable total formé par ces trois changements ait la valeur zéro) mesurera le changement, par exemple en ergs. Seront mesurés par des nombres positifs les échauffements, et de façon générale tous les changements efficients que peut payer l’abaissement d’un poids.
C’est ainsi que nous pouvons regarder comme mesurable au point de vue thermodynamique tout changement défini par l’état initial et l’état final d’une enceinte où naissent et se développent des plantes et des animaux. Si nous disons que, pendant un an, le changement de ce système est de ceux qui valent tant de kilogrammètres et tant de millions de calories, il est clair au reste que nous ne prétendons pas exprimer toutes les qualités intrinsèques de ce changement (où par exemple ont pu se développer des êtres capables de pensée), (pas plus que nous ne prétendons dire que tous les objets de même poids ont les mêmes propriétés).
33. L’énergie. — Nous avons obtenu le principe d’équivalence par généralisations successives où s’expriment des analogies profondes entre groupes sans cesse plus vastes de phénomènes. Nous avons ainsi atteint un énoncé purement descriptif dégagé de toute obscurité métaphysique et de toute hypothèse sur des propriétés cachées de la matière.
Cet énoncé, pourtant, ne satisfait pas notre esprit. Nous avons exprimé une idée claire d’une extrême importance, mais nous sentons confusément qu’il y a, derrière les faits perçus par nos moyens actuels d’investigation, une chose plus profonde où gît la raison secrète de cette équivalence des enchaînements dont nous savons à présent qu’elle est nécessaire, mais sans comprendre comment elle se réalise. Nous sommes loin de saisir le mécanisme fin qui entraînerait, comme nécessité logique, cette équivalence qui ne nous apparaît encore que comme règle empirique. Mais c’est déjà percevoir quelque chose que de deviner des contours derrière un brouillard, si l’on sait reconnaître ce qu’il y a de vague en ces contours. Aussi n’hésiterons-nous pas, reprenant en définitive, en l’élargissant, la vieille hypothèse du Calorique, à introduire une notion incomplète encore et confuse, par où nous espérons approcher de la compréhension profonde du Principe d’Équivalence.
À cette fin, nous dirons que tout changement efficient d’un système marque le gain ou la perte, par ce système, d’une certaine quantité d’une Chose que nous appelons Énergie, non perçue par nos sens, mais dont l’accroissement (positif ou négatif) est mesuré par le même nombre que le changement. Nous pourrions soutenir que nous entendons simplement par là que l’aptitude du système à produire des changements résistants (tel une élévation de poids) a augmenté si le changement est positif, et diminué s’il est négatif. Mais, je le répète, ce que nous voulons dire est qu’il existe une chose protéiforme, l’Énergie, dont nous savons mesurer la variation, qui entre dans tout système subissant un changement positif, et qui sort de tout système subissant un changement négatif.
Comprenons que cette Chose est indestructible.
34. Conservation de l’énergie. — Nous avons expliqué comment tout changement efficient d’un système s’accompagne nécessairement, dans un autre système, d’un autre changement efficient, dont la valeur numérique est égale, avec le signe contraire, à celle du premier changement.
Si donc l’énergie interne d’un système augmente, il y a diminution égale de l’énergie interne d’un autre système : comme la Matière, l’Énergie se déplace en se conservant. C’est là le Principe de la Conservation de l’Énergie.
En particulier, si un système demeure isolé, son énergie demeure constante, mais nous n’avons encore aucun moyen de mesurer l’énergie totale d’un système, et savons seulement mesurer sa variation.
Si, même quand un système n’est pas resté isolé, il a subi un changement en définitive sans répercussion extérieure, son énergie est demeurée constante. Par exemple, les expériences sur la détente des gaz (13) montrent que :
À température fixée, l’énergie d’une masse gazeuse est fixée.
On reconnaîtra, dans le Principe de la Conservation de l’Énergie, l’élargissement de la vieille hypothèse de l’indestructibilité du Calorique. Tous l’avaient acceptée jadis, et depuis tous l’avaient abandonnée, au lieu d’y voir une ébauche déjà précieuse d’une conception féconde. Loin de nous ranger avec ceux qui semblent éprouver de la satisfaction à déclarer la faillite successive des théories, nous éprouverons du réconfort à saisir sur cet exemple qu’un grand effort de l’Intelligence humaine ne reste généralement pas stérile.
FORMES DE L’ÉNERGIE
Nous distinguerons autant de formes de l’énergie que nous pourrons distinguer de types de changements efficients, impliquant un apport d’énergie s’ils sont positifs, un départ s’ils sont négatifs.
35. Énergies potentielles. — La connaissance des divers genres de travaux conduit à définir les diverses énergies potentielles.
Un ressort que l’on comprime ou distend emmagasine par ce fait de l’énergie potentielle élastique, qui abandonnera le ressort quand il se détendra, par exemple lorsque l’arc qu’on avait bandé se détendra en lançant une flèche.
C’est encore de l’énergie potentielle qui s’emmagasine dans un système de masses qui s’attirent, lorsqu’on les écarte les unes des autres, ce qu’on a pu obtenir par descente de poids, c’est-à-dire au fond par dépense d’énergie potentielle de gravitation. Symétriquement, de l’énergie potentielle est sortie d’un système où des masses qui s’attirent se sont rapprochées les unes des autres.
On se demandera où peut être localisée cette énergie potentielle, étant donné que des corps qui s’attirent ne subissent aucun changement intrinsèque du fait qu’ils s’approchent ou s’éloignent les uns des autres. Pour essayer de le comprendre, rappelons-nous (V, 41) que toute force appliquée à un point matériel est nécessairement exercée par l’espace où ce point est situé, espace qui a une réalité physique, et non pas seulement géométrique. Ainsi nous devrons admettre, sans savoir en dire plus, que par exemple l’énergie potentielle de gravitation est une modification physique de l’espace où baignent les corps qui s’attirent, fonction de l’écartement de ces corps, et d’autant plus grande qu’ils sont plus écartés. Nous envisagerons de même par la suite les énergies potentielles électrique et magnétique.
36. Potentiel de gravitation. — Considérons le champ de gravitation créé par une masse . Le travail qu’il faut dépenser pour amener du point donné A jusqu’à un autre donné B, une petite masse située à la distance de M est en grandeur et en signe ( étant la constante de gravitation) :
expression évidemment indépendante du chemin suivi entre A
et B. Si le champ est dû à plusieurs masses, ce travail devient :
Le quotient de ce travail par la petite masse déplacée, ou, en d’autres termes, le travail nécessaire pour amener l’unité de masse de A en B définit l’excès du potentiel en B sur le potentiel en A, relativement aux masses qui créent le champ.
Ainsi, au facteur près, cet accroissement de potentiel est mesuré par l’accroissement de l’expression (étendue à toutes les masses qui créent le champ) quand on le calcule d’abord en A, puis en B.
Nous penserons que le potentiel est une propriété de l’espace où baignent les masses qui s’attirent, propriété physique non perçue par nos sens, mais dont nous savons mesurer la variation entre deux points, par la variation de la fonction . L’un de ces points, arbitrairement fixé (l’autre variant) pourra être pris pour origine des potentiels. Si cette origine est prise à l’infini, nous aurons, pour tout point :
Une surface équipotentielle est définie par la condition que le potentiel y est constant (il ne faut aucun travail pour transporter une masse d’un point à un autre d’une telle surface).
Soient , deux surfaces équipotentielles très voisines (fig. 10), avec différence de potentiel Soit un point quelconque sur
, et sur un point voisin de . 
Fig. 10. Si est la composante du champ dans la direction , nécessairement est égal à ; est donc maximum et devient le champ en quand est normal à ; en chaque point d’une surface équipotentielle le champ est perpendiculaire à la surface (fig. 10). Donc la ligne de force qui passe par un point quelconque d’une surface équipotentielle, étant tangente au champ, est normale à la surface équipotentielle.
37. L’énergie potentielle de gravitation. — L’énergie potentielle de gravitation d’un système de masses se calcule comme il suit : soit, au point où se trouve l’une de ces masses, le potentiel dû aux autres masses (origine des potentiels à l’infini). Imaginons la distribution de même configuration, mais où toutes les masses (et par suite le champ en chaque point) seraient multipliées par un facteur inférieur à 1 ; en sorte que le potentiel au point où est la masse serait . Pour amener cette distribution de l’état à l’état on pourrait amener de l’infini les masses ou en recevant le travail :
Pour passer de l’état où est nul (pas de masses) à l’état où est égal à 1 (configuration donnée), il faudrait donc recevoir :
Cette expression mesure la diminution de l’énergie potentielle quand les masses, d’abord infiniment éloignées les unes des autres, prennent leur distribution actuelle. Par exemple, deux masses à la distance , ont perdu par leur rapprochement l’énergie potentielle qui deviendrait infinie si ces masses pouvaient se rapprocher indéfiniment, ce qui indique, ou que toute masse finie a une dimension minimum, ou que la loi de Newton cesse de s’appliquer à très petite distance.
Nous développerons des considérations de même genre pour les énergies potentielles électrique et magnétique (VIII, Électricité).
38. Énergie de mouvement. — Des corps en mouvement par rapport au sol constituent une réserve d’énergie, un « capital », qui permet, par l’arrêt de ces mouvements, d’acheter une quantité définie de travail résistant, ou d’énergie potentielle. Par le fait de leur mouvement, ces corps possèdent donc une forme d’énergie qui est dite énergie de mouvement, ou énergie cinétique (peut-être d’abord considérée au xviiie siècle).
Il faut prendre garde toutefois qu’un corps en mouvement, disons un obus de 10 kilogrammes animé par rapport au sol d’une vitesse de 500 mètres par seconde, ne possède pas plus en soi d’énergie de mouvement qu’il ne possède une vitesse absolue. C’est le système sol-obus, avec vitesse relative de 500 m/sec., qui possède cette énergie. Il faut au moins deux objets en mouvement l’un par rapport à l’autre pour constituer une réserve d’énergie cinétique, sous une forme qui n’est localisée dans aucun d’eux et se manifeste seulement quand, par un mécanisme quelconque, leur vitesse relative change.
Ou encore, pour un objet donné qui généralement est en mouvement par rapport aux divers référentiels de Galilée, l’énergie cinétique dépend du référentiel avec lequel on le solidarise en l’y arrêtant. Elle n’est aucunement fixée de manière intrinsèque. De même (et l’analogie n’est pas superficielle) la fréquence d’une lumière dépend du référentiel où on l’observe (c’est-à-dire où on l’arrête).
Tout référentiel de Galilée est, à cet égard, isotrope. Le dégât que produit en s’y arrêtant un projectile donné, ou de façon plus précise le travail résistant qu’il peut y produire en s’y arrêtant, dépend de la vitesse relative, mais non pas de la direction de cette vitesse. Ce travail, ou l’énergie cinétique alors disparue, qui ne change pas avec le signe de la vitesse, est donc une fonction du carré de cette vitesse.
Nous avons vu qu’on peut « acheter » (12) avec un travail un lancement de mobile, c’est-à-dire acheter de l’énergie cinétique avec de l’énergie potentielle. Comme l’énergie se conserve, nous voyons, de façon générale, que :
Quand en un référentiel de Galilée, pour un système de mobiles, variations d’énergie cinétique et d’énergie potentielle épuisent exactement leurs effets les unes par les autres, la somme de l’énergie cinétique et de l’énergie potentielle, définies à chaque instant par les positions et les vitesses des points matériels du système, demeure constante.
39. L’énergie cinétique est proportionnelle à la masse et au carré de la vitesse. — Nous venons de comprendre que, pour un point matériel, et disons relativement au sol (dans la mesure où celui-ci peut être regardé comme un référentiel de Galilée) l’énergie cinétique est une fonction du carré de la vitesse. Nous allons le démontrer et trouver cette fonction, en observant comment ce point matériel aurait pu prendre cette vitesse en chute libre, ou plus généralement sous l’action d’une force constante.
Considérons à cette fin un point matériel de masse , d’abord au repos, lancé par l’action d’une force constante qui lui imprime l’accélération constante (voir V, 4). Après un temps , la vitesse est , l’espace parcouru est et le nombre qui mesure l’énergie cinétique acquise aux dépens du travail égale numériquement à ce travail, peut donc s’écrire, en nous rappelant la loi d’inertie, et la définition de la masse :
Ainsi l’énergie cinétique est proportionnelle à la masse et au carré de la vitesse, les choix précédemment faits pour les unités fixant à la valeur du coefficient de proportionnalité.
40. La masse, capacité d’énergie cinétique. — Pour un autre point matériel, de masse , animé aussi de la vitesse , on a de même :
en sorte que :
Ainsi le rapport des énergies cinétiques, pour deux mobiles de même vitesse ne dépend pas de cette vitesse : s’il faut travailler 3 fois plus pour lancer le premier avec une vitesse que pour lancer le second avec cette même vitesse , il faut également travailler 3 fois plus pour imprimer au premier une autre vitesse que pour imprimer au second cette même autre vitesse . Cette invariance aurait permis de définir les rapports d’inertie ou de masse de deux objets. Ou encore, nous pouvons dire que le premier objet, 3 fois plus inerte, 3 fois plus massif, et 3 fois plus pesant, a une capacité 3 fois plus grande pour l’énergie cinétique, aussi bien que pour l’impulsion (V, 17).
41. Énergie cinétique et impulsion. — Il n’est pas inutile de comparer, à ce point de vue, les deux réalités physiques énergie cinétique et impulsion.
L’une est homogène à un travail, l’autre à un effort. Soient deux points matériels de masses et animés respectivement des vitesses et . À impulsions égales, leurs énergies de mouvement sont entre elles dans le rapport inverse de leurs masses ; à énergies cinétiques égales, leurs impulsions sont entre elles comme le rapport des racines carrées de leurs masses.
Par exemple, si un grain de plomb de 2 millimètres de diamètre et un boulet de plomb de 20 centimètres de diamètre (donc 1 million de fois plus lourd) ont mêmes impulsions, l’énergie cinétique du grain vaut 1 million de fois celle du boulet. Si ce sont leurs énergies cinétiques qui sont égales, l’impulsion du boulet ne vaut que 1000 fois celle du grain.
42. Énergie cinétique d’un système solide, qui tourne sur lui-même tout en se déplaçant. — Considérons un solide libre en mouvement dans un référentiel de Galilée. Quel travail pouvons-nous obtenir en y immobilisant ce solide, rien d’autre ne se produisant ?
Soit le centre d’inertie (coordonnées , , ) qui se meut d’un mouvement rectiligne uniforme (V, 24), et soient les axes menés par parallèlement aux axes liés au référentiel. Pour tout point du solide, nous avons
L’énergie cinétique , égale à ou à
peut donc s’écrire ( égal à , à , à ) :
Or, est le carré de la vitesse de par rapport aux axes entraînés par ; est le carré de la vitesse de par rapport au référentiel ; enfin dérivée de qui est égale (IV, 30) au produit de par la coordonnée du centre de gravité selon l’axe laquelle est forcément nulle, est nulle, et de même sont nulles et . Il reste donc :
Le premier terme du second membre est l’énergie cinétique d’une masse égale à la masse totale du solide, concentrée en son centre d’inertie. Le second terme est l’énergie cinétique d’un solide libre autour d’un point fixe d’un référentiel de Galilée, c’est-à-dire une énergie de rotation, autour d’un axe passant par ce point (I, 19).
Bref, le travail rendu disponible par immobilisation est la somme d’une énergie de translation et d’une énergie de rotation (voir V, 29). Si par exemple un disque est lancé à plat sur un plan horizontal poli bien lubréfié (V, 1), on pourra immobiliser son axe, ce qui épuisera son énergie de translation, après quoi il tournerait encore indéfiniment autour de cet axe devenu immobile, puis on pourra immobiliser son pourtour, ce qui épuisera son énergie de rotation.
De façon générale, l’énergie de rotation d’un solide tournant avec la vitesse angulaire autour d’un axe lié au sol (tel un volant de machine) sera ( désignant la distance à l’axe de la parcelle de masse ) :
étant le moment d’inertie (V, 31) autour de l’axe de rotation.
43. Énergie calorifique ou chaleur. — Nous venons de caractériser deux formes remarquables d’énergie, l’énergie potentielle et l’énergie cinétique. Une autre forme remarquable apparaît en considérant l’énergie interne d’un thermostat, système qui, avons-nous dit, ne connaît l’extérieur que par actions thermiques (7). Selon que ce thermostat subit un changement positif ou négatif, nous dirons qu’il y entre ou qu’il en sort une certaine quantité de chaleur, ou, plus simplement, une certaine chaleur. Dans l’expérience de Joule par exemple (26), de l’énergie potentielle abandonne les poids moteurs, se transformant transitoirement en énergie cinétique (à chaque instant peu importante) puis entre et reste dans le calorimètre sous forme de chaleur, sans cesse accrue à mesure que les poids descendent.
Tentons d’analyser ce mécanisme avec plus de finesse : nous verrons que le mouvement des palettes se communique au liquide, où il se dissémine entre parties sans cesse plus petites, accroissant en définitive cette agitation interne désordonnée que possède tout liquide du fait qu’il est à une certaine température et qui se traduit à l’échelle microscopique par le mouvement brownien (IV, 42). Ce qui nous amène à penser que l’énergie thermique présente dans une masse d’eau par exemple apparaîtrait à un grossissement suffisant comme une somme d’énergies potentielles et cinétiques en transformation réciproque incessante, et réparties, selon un régime permanent fixé à chaque température, entre un nombre immense de systèmes excessivement petits.
Cette conception n’est d’ailleurs pas indispensable et nous pouvons considérer l’énergie thermique comme une forme spéciale d’énergie sans chercher à l’analyser. Nous ne saurions pas au reste faire cette analyse dans le cas d’un solide, disons du cuivre, dont la température s’élève et qui de ce fait emmagasine de l’énergie thermique.
44. Énergies chimiques. — Plus généralement, nous avons vu (31) que tout changement efficient d’un système peut s’obtenir en faisant pénétrer dans ce système à la fois de l’énergie mécanique (travail ou énergie cinétique) et de l’énergie thermique (chaleur). C’est le cas par exemple pour une liquéfaction isotherme sous la pression de saturation ; ou, pour faire intervenir une réaction chimique, c’est le cas pour la formation de carbonate de chaux à température et pression constantes par action du gaz carbonique sur de la chaux. L’accroissement d’énergie du système sera numériquement égal à la somme des énergies qui y auront alors pénétré par voie mécanique ou par voie thermique. Ce sera le cas pour toute énergie chimique, dont chacune constitue en elle-même une forme particulière d’énergie.
45. Énergie lumineuse. — Déjà nous avons signalé que la disparition ou l’apparition de lumière sont des changements efficients ne pouvant se produire sans répercussion. Par exemple, la lumière du soleil, absorbée par un corps, l’échauffe, y faisant apparaître de l’énergie thermique, en même temps qu’elle disparaît.
De l’énergie lumineuse est toujours présente, bien que en quantité minime dans les conditions ordinaires, au sein de tout objet, du fait même qu’il est nécessairement à une certaine température. Nous avons en effet déjà compris (8) qu’une enceinte isotherme vide de matière contient de la radiation qui se révèle comme lumière analysable au spectroscope quand on la laisse s’enfuir au travers d’une petite ouverture pratiquée dans la paroi de l’enceinte, où elle se régénère continuellement avec une densité fixée tant que la température est maintenue constante. Cette paroi intérieure, qui garde le même état tant que sa température demeure la même, débitera la même quantité de lumière si on laisse entrer dans l’enceinte de la matière qui s’imprégnera donc de lumière, en prenant la température de l’enceinte, jusqu’à réalisation d’un régime permanent où cette matière débite autant qu’elle reçoit. Nous concevons ainsi comment un bloc de matière ordinaire rayonne vers l’extérieur par le seul fait qu’il est à une certaine température, la lumière dont il est imprégné, et qu’il régénère sans cesse. La densité d’énergie lumineuse ainsi présente et maintenue constante dans chaque substance de température donnée est, comme nous verrons, infime relativement à l’énergie thermique dans les conditions qui nous sont ordinaires ; elle prendrait de l’importance, au sein de matière très raréfiée et à très haute température, comme à l’intérieur d’une étoile.
Nous pourrons bientôt établir (VIII, Électricité, 80) que l’énergie lumineuse d’une lumière simple est transportée par des photons minuscules identiques, dont la Théorie de l’émission (II, Lumière, 1, 3, 35) avait deviné l’existence.
Puisque la fréquence d’une lumière simple dépend du référentiel de Galilée où on l’observe, c’est-à-dire où on l’absorbe (II, 36 et III, 10), l’énergie que peut céder un photon, cependant en soi donné, dépend du référentiel de Galilée où il disparaît sans avoir été ralenti. C’est aussi le cas pour l’énergie que l’on peut tirer de l’arrêt d’un mobile dans ce référentiel. Mais le mobile s’arrête progressivement et ne disparaît pas : on voit combien diffèrent profondément les photons et les grains matériels.
MASSE DE L’ÉNERGIE
46. Réalité de l’énergie. — Malgré ce qu’a de séduisant la conception de l’énergie indestructible, on pouvait soutenir encore il y a peu d’années que cette conception n’apporte rien qui ne soit contenu dans le Principe d’Équivalence. On ne le peut plus depuis qu’Einstein a montré que la masse d’un système matériel varie proportionnellement à son énergie interne, ce qui du même coup assigne une limite supérieure à l’énergie que peut perdre ce système matériel. Résultat capital, que nous allons obtenir par un raisonnement ultérieur plus simple dû à Paul Langevin.
47. Équations de Langevin. — La forme que je viens de donner au Principe d’Équivalence, et la définition qui en résulte pour l’Énergie, antérieures à la théorie de la Relativité, ont résisté aux remaniements que cette théorie a imposés en Énergétique. Et Paul Langevin a prouvé, par la belle démonstration qu’on va lire[6] que à la condition d’appliquer en « Relativité » le Principe d’équivalence ainsi compris, on peut établir l’Inertie de l’Énergie et calculer cette inertie.
Nous considérerons le changement défini par l’arrêt, relativement à un référentiel stellaire, d’un mobile d’abord animé de la vitesse dans ce référentiel, étant admis que rien d’intrinsèque ne s’est passé dans le mobile, en sorte que des observateurs liés à ce mobile lui trouvent exactement les mêmes propriétés, soit quand il est animé de la vitesse soit quand il est arrêté.
Nous avons déjà établi au moins en première approximation et nous regardons comme rigoureusement exact, que la direction de la vitesse n’intervient pas dans la valeur du changement « arrêt » (isotropie de tout référentiel de Galilée). Ce changement, ou énergie cinétique , sera donc mesuré par un nombre de la forme , la fonction devant être la même pour tous les référentiels stellaires ou référentiels de Galilée, puisque la Physique y est la même (Principe de Relativité). Toutes les observations d’effets produits par des arrêts de projectiles concordent pour suggérer que cette fonction est continue et a une dérivée ; nous l’admettrons.
Nous allons réussir à déterminer cette fonction en considérant deux processus différents d’arrêt du mobile.
Soient deux référentiels stellaires , , (« wagons ») animés, par rapport à un troisième (« voie »), de vitesses égales et contraires et . Nous imaginerons un couple de mobiles identiques , animés par rapport au « wagon » de vitesses égales et contraires et et un couple identique , par rapport au « wagon » .
Nous supposerons d’abord (I) que et sont perpendiculaires à la direction de glissement de ou sur . Alors, par raison de symétrie, les vitesses de , et , relativement à la « voie » auront même valeur absolue (fig. 11, I).
Puis nous supposerons (II) que et sont parallèles à la direction de glissement des « wagons » sur la « voie ». Si alors, par rapport à cette « voie », la vitesse de est celle de est (conditions symétriques) et si celle de est celle de est (fig. 11, I).
Discutons d’abord le cas (I). Nous pouvons arrêter simultanément les quatre mobiles par rapport à la « voie ». Par exemple au moyen de cordons qui leur feront simultanément actionner les palettes d’un calorimètre de Joule en repos relativement à la « voie » et qui, par raison de symétrie, ne recevra aucune impulsion ; le changement produit dans ce calorimètre, changement qui paie le quadruple arrêt, sera .
— Mais nous pouvons aussi arrêter nos mobiles , , par rapport au « wagon » et nos mobiles par rapport au « wagon »
puis alors seulement les arrêter par rapport à la « voie ». Et l’ensemble des changements ainsi produits, qui doit encore payer
le quadruple arrêt par rapport à la voie, devra aussi être égal à
. Calculons cette somme :
L’arrêt relativement à des mobiles pourra se faire par cordons actionnant les palettes d’un calorimètre de Joule immobile dans ce wagon, et qui ne recevra aucune impulsion ; le changement de ce calorimètre, qui paie l’arrêt dans le wagon sera . De même l’arrêt de dans le wagon aura la valeur . Soit, en tout, pour les arrêts dans les deux wagons.
Mais les calories développées dans chaque wagon (par exemple sous forme de glace fondue), en repos relativement à ce wagon, ne sont pas en repos relativement à la voie. Or, il n’y a aucune raison pour que la fusion d’un morceau de glace en mouvement par rapport à la voie ait la même valeur que la fusion du même morceau de glace au repos (ou, si on préfère, on ne reçoit peut-être pas la même énergie en arrêtant le morceau de glace ou l’eau qui provient de sa fusion). Du moins, ici encore, la direction du mouvement ne peut avoir d’importance, nos référentiels étant isotropes. Si est la valeur d’une calorie immobile, la valeur de cette calorie animée de la vitesse sera . Cela nous donne pour valeur de l’arrêt des mobiles dans les wagons animés par rapport à la voie des vitesses et
Enfin, reste à arrêter par rapport à la voie les 2 mobiles maintenant au repos dans et les 2 mobiles maintenant au repos dans . Ce qui pourra se faire au moyen de cordons actionnant simultanément les palettes d’un dispositif de Joule sans lui communiquer d’impulsion (par raison de symétrie) en y produisant le changement . De sorte qu’au total on aura :
Bref, les fonctions et devront vérifier l’identité
| . | (I) |
(où est la vitesse résultant de la composition des deux vitesses rectangulaires et ).
Discutons maintenant le cas (II), supposant les parallèles aux . Ici encore nous pourrons utiliser deux processus différents : nous arrêterons simultanément, sur la voie, et par dispositif de Joule qui ne recevra pas d’impulsion, et de même simultanément et ; ou bien nous arrêterons d’abord chaque couple dans le wagon correspondant, puis nous arrêterons sur la voie les 4 mobiles maintenant animés des vitesses ou . Raisonnant comme dans le cas (I), nous obtiendrons ainsi l’équation fonctionnelle :
ou
| . | (II) |
Ces équations fonctionnelles (I) et (II) obtenues par application du Principe d’Équivalence vont déterminer les fonctions et si nous tenons compte de la formule de composition des vitesses. En première approximation nous utiliserons la formule établie (I, 23) dans l’hypothèse où la notion de simultanéité est valable ; en seconde approximation (grandes vitesses) nous utiliserons la formule générale d’Einstein (III, 8).
48. Valeur de l’énergie cinétique pour de faibles vitesses. — En première approximation, nous avons, pour résultante de vitesses rectangulaires et
L’identité (I) devient donc :
c’est-à-dire, si nous écrivons au lieu de et au lieu de
Dérivons par rapport à , nous obtenons :
qui impose en particulier :
d’où résulte que l’équation précédente peut s’écrire :
Hors le cas singulier, provisoirement réservé, où serait une constante auquel cas serait égal à et identiquement égal à 1, cette équation (où l’on reconnaît l’équation qui définit la fonction exponentielle) n’est vérifiée que par la fonction
| ( arbitraire). |
Intégrant, et tenant compte de ce que l’énergie cinétique est nulle pour nul, on trouve
Introduisons dans (II) ces expressions de et ; nous obtenons, après division par (ce qui réserve le cas de nul) :
ou, après simplifications évidentes
Or, en première approximation, les étant parallèles aux
ce qui donne pour l’équation précédente :
vérifiée seulement pour égal à 1, donc précisément pour nul. Mais alors est égal à la constante et à en même temps que devient égal à 1 : nous retombons sur le cas singulier réservé. Cette solution seule possible convient en effet, les équations de Langevin, (y remplacer les en fonction des et ) étant alors vérifiées.
Ainsi, pour de faibles vitesses, est égal à 1, ce qui signifie que la calorie en mouvement coûte le même prix que la calorie en repos. D’autre part, est égal à (qu’on peut écrire ), ce qui signifie que l’énergie cinétique est pour un objet donné proportionnelle au carré de la vitesse. Nous retrouvons la loi d’abord obtenue (V, 7) en supposant connue la loi de la chute des corps, puis établie (V, 31) en combinant déjà, de façon différente, le Principe de relativité avec la règle de composition des « faibles » vitesses.
49. Expression de l’énergie cinétique valable pour toute vitesse réalisable. — Combinons maintenant, en seconde approximation le Principe d’Équivalence et la formule générale de composition des vitesses.
Nous avons à voir ce que deviennent alors les équations fonctionnelles de Langevin.
Dans le cas (I) (les perpendiculaires aux ) chaque vitesse résultante prend l’expression (III, 8) :
L’équation fonctionnelle (I) devient donc :
qui va reprendre une forme déjà discutée si nous posons, comme nous le pouvons :
avec
d’où résulte pour , c’est-à-dire pour , la valeur en sorte que notre équation fonctionnelle (I) prend une forme
que nous venons de discuter et qui impose
| . |
D’autre part notre équation fonctionnelle (II) s’écrit, après division par (ce qui réserve le cas de nul) :
d’où :
Or (les étant parallèles aux ) il faut écrire (Einstein) :
en sorte que
et notre équation (II) devient donc, après division par le facteur
commun :
équation du type connu :
qui n’est vérifiée (avec différent de zéro) que si est nul ou égal à comme on voit en dérivant par rapport à .
L’hypothèse, déjà réservée, de nul, entraînerait égal à 1 et égal à . Mais alors l’équation II, (y exprimer les en et par les formules d’Einstein), n’est pas vérifiée. Reste donc seule possible pour la valeur ce qui entraîne :
expressions qui vérifient en effet les équations de Langevin.
L’énergie cinétique , égale à peut donc s’écrire, développant en série :
qui pour petit se réduit au premier terme lequel doit
alors se confondre avec de sorte que :
et que l’énergie cinétique de la masse animée de la vitesse
est donnée pour toute vitesse par la formule
qui se réduit bien à pour petit, comme on voit en développant en série , et qui devient infinie quand tend
vers .
Nous avons ainsi obtenu l’expression de l’énergie cinétique pour les grandes vitesses, énergie qui devient infinie quand la vitesse du mobile tend vers celle de la Lumière. Cela s’accorde avec l’impossibilité (II, 26) que la Matière puisse atteindre la vitesse de la Lumière.
Sur cette même formule, nous voyons que, même aux plus grandes vitesses, les énergies cinétiques de deux mobiles qui ont même vitesse sont entre elles comme leurs masses : s’il a fallu 3 fois plus de peine pour communiquer à un mobile une certaine vitesse que pour la communiquer à un mobile , il faudra se donner 3 fois plus de peine dans le cas de n’importe quelle autre vitesse, si grande soit-elle. La masse définie aux faibles vitesses mesure pour toute vitesse la capacité d’énergie cinétique et sa définition comme telle (38) subsiste alors que la définition par la loi d’inertie aurait pu présenter des difficultés. La masse garde pour toute vitesse sa signification essentielle. On voit pourquoi nous n’avons pas voulu adopter les expressions de « masse longitudinale » et « masse transversale ».
50. Inertie de l’énergie. Loi d’Einstein. — Maintenant il est facile de montrer que la masse d’un système matériel où s’effectuent des changements efficients, en sorte qu’il perd ou gagne de l’énergie, varie en proportion de l’énergie perdue ou gagnée.
Soit un système de masse , (disons de la glace) en repos dans un référentiel stellaire, capable de subir un changement efficient (ce sera par exemple la fusion de cette glace qui a même valeur dans tout référentiel stellaire.
Soit placé un tel système dans chacun de nos deux « wagons » et animés de vitesses égales et contraires et par rapport à notre « voie » .
Nous pouvons alors de deux manières différentes, réaliser le changement que nous allons dire :
a) nous pouvons arrêter, par rapport à , au moyen d’un dispositif de Joule, les deux corps avant de les changer, ce qui fournira déjà l’énergie
puis alors les changer (fondre la glace) en leur fournissant à chacun l’énergie , ce qui en définitive donne pour valeur du changement
global
b) ou bien nous pouvons, de la voie, changer les deux corps (fondre la glace) en laissant chacun immobile dans son « wagon », ce qui exigera pour l’énergie des calories ainsi créées en mouvement par rapport à la voie :
puis nous pouvons arrêter les systèmes ainsi transformés (eau de fusion), et dont la masse a pu varier et devenir , ce qui nous fournira l’énergie
Égalant ces deux expressions de ce même changement nous avons :
ou simplement :
ou, en langage ordinaire (loi d’Einstein) :
La masse d’un corps dont l’énergie interne varie s’accroît d’une masse égale au quotient de l’accroissement d’énergie interne par le carré de la vitesse de la lumière.
Cette masse entre avec l’énergie, subsiste avec elle, sort avec elle, en est inséparable. Bref :
Toute énergie a une inertie, mesurée par le quotient de sa valeur par le carré de la vitesse de la lumière.
Ceci s’applique à toutes les formes d’énergie : potentielle, cinétique, thermique, chimique, lumineuse. Il est particulièrement intéressant de comprendre qu’un corps lumineux, le Soleil par exemple, perd continuellement de la masse, transportée par la Lumière qui le fuit.
51. Origine du rayonnement des étoiles. — Nous voici amenés à discuter l’origine du prodigieux rayonnement qui jaillit intarissablement des étoiles. Notre Soleil, par exemple, envoie par minute 2 calories sur chaque centimètre carré de surface terrestre normale aux rayons, soit en tout, par seconde, environ ergs (qui, selon la découverte d’Einstein, ont une masse gr. soit environ quatre millions de tonnes par seconde).
J’ai insisté sur ce que, d’après les sédiments où l’on trouve des vestiges d’êtres analogues à certains mollusques actuels, les conditions climatériques, qui sont réglées par ce rayonnement, ont peu changé depuis un temps probablement bien supérieur à un milliard d’années. (Le Soleil a rayonné pendant ce temps plus que le millième de sa masse actuelle).
Il n’y a pas de combustion connue qui pourrait expliquer même quelques milliers d’années de ce rayonnement. Une explication moins insuffisante fut proposée par Lord Kelvin, qui plaçait l’origine de la chaleur solaire dans l’énergie de gravitation libérée par la condensation de la masse solaire à partir d’une masse nébuleuse primitive très raréfiée (37). Supposant toutes les parcelles solaires venues de distances infinies, lord Kelvin estimait qu’il expliquait au plus une quinzaine de millions d’années du rayonnement au taux actuel. Curieusement, il allait jusqu’à dire que, « puisqu’il n’y a pas d’autre explication possible », il faut que les géologues fassent tenir l’évolution des êtres vivants dans cette durée !
Mais même un grand physicien ne peut assigner de limite aux possibilités de la Nature. Et, depuis, on a découvert, avec les transmutations, des transformations matérielles dégageant colossalement plus d’énergie que nos réactions chimiques les plus violentes. J’ai fait observer, en même temps qu’Eddington (1919) qu’il suffisait que le soleil primitif eût été fait d’hydrogène, qui probablement peut se transformer en hélium avec perte de un centième de sa masse, soit un dégagement de 250 milliards de calories par gramme, pour expliquer cent milliards d’années de rayonnement solaire au taux actuel. Durée où l’Évolution ne manque plus de temps ! Et d’autres transformations plus profondes, qui donneraient au rayonnement d’une Étoile, au taux actuel avec évanouissement presque total en Lumière, une durée supérieure au trillion d’années, ont pu être imaginées.
Si une quantité donnée de matière peut perdre toute sa masse, elle perdra, par gramme initial, l’énergie ergs. Telle est l’énergie maximum qu’on peut espérer extraire de matière en repos dans un référentiel stellaire. Mais dans un autre référentiel de vitesse par rapport au premier, on en pourrait extraire au total l’énergie
qui n’a pas de limite théorique actuelle.
52. Pression de radiation. Impulsions reçues ou communiquées par la lumière. — Considérons une paroi que frappe normalement de la Lumière, c’est-à-dire que frappe (nous le savons maintenant) de la masse (qui n’est pas de la Matière) cheminant avec la vitesse de la Lumière. Il nous est alors difficile de ne pas évoquer le cas d’une paroi qui reçoit une grêle de projectiles (V, 26) et qui subit, de ce fait, une pression numériquement égale à l’impulsion des projectiles arrêtés.
Ceci conduit à penser que la Lumière exerce une « pression de radiation » sur un obstacle qui l’absorbe (ou sur lequel elle prend appui si elle est réfléchie ou émise) ; et que cette pression sera numériquement égale à l’impulsion attribuable à la Lumière (aux photons absorbés ou émis).
Cette pression, prévue par divers physiciens (notamment par le physicien italien Bartoli, et par le physicien anglais Maxwell, dès 1874) pour d’autres raisons que nous indiquerons par la suite, existe, en effet, et elle est mesurable (Lebedef, Poynting, etc.). On peut le constater, par exemple, en éclairant par un rayon lumineux (flux d’énergie mesuré au calorimètre) une palette verticale fixée à un bout d’un fléau soutenu par un fil de torsion (comme dans la balance de Coulomb) ; le fléau tourne jusqu’à ce que le couple de torsion équilibre celui exercé par la pression de radiation, ce qui mesure cette dernière.
On s’est ainsi assuré que la pression de radiation existe, et qu’elle est (selon la prévision de Maxwell) numériquement égale à l’énergie contenue dans le cylindre de lumière incident ayant la longueur 1 et la section 1. Nous admettrons ici, comme loi expérimentale, cette égalité entre et .
Cette pression de radiation doit être égale (V, 26) à l’impulsion transportée par la lumière, contenue dans le cylindre de section 1 et de longueur , qui vient frapper la paroi pendant l’unité de temps. L’énergie de cette quantité de lumière est , donc sa masse est ou .
L’impulsion de cette masse de lumière étant , ou , est donc égale à soit . En d’autres termes :
L’impulsion possédée par une masse donnée de lumière a même mesure que le produit de cette masse par la vitesse de la Lumière :
de même que l’impulsion d’une masse matérielle animée de la vitesse a même mesure que le produit de cette masse par sa vitesse.
La loi de conservation de l’impulsion restera applicable : la masse de lumière qui s’absorbe dans un obstacle de masse lui communiquera une vitesse telle que
Réciproquement, si la lumière est émise (ou réfléchie) une impulsion égale sera communiquée par recul à la matière.
La conservation de la quantité de mouvement ou impulsion du système isolé, s’étend ainsi à un système contenant de la Matière et de la Lumière (émise ou absorbée).
53. L’énergie est pesante. Expression générale de la gravitation universelle. — Tout système matériel est pesant, d’un poids exactement proportionnel à sa masse. Nous n’avons aucune raison, aucun moyen, de distinguer dans cette masse une fraction attribuable à la Matière, et une fraction attribuable à l’énergie qu’elle transporte. (L’hydrogène qui perd de l’énergie en devenant de l’hélium perd en effet du poids aussi bien que de la masse).
Nous devons donc prévoir que l’énergie sous toutes ses formes est pesante aussi bien que massive. En particulier les photons dont nous démontrerons (VIII) qu’ils transportent l’énergie de la Lumière sont pesants, et nous devons nous attendre à ce que le rayon de lumière qui passe auprès d’une étoile soit dévié par elle (Einstein) bien que très faiblement en raison de son énorme vitesse. Ce qui a été vérifié, au cours d’une éclipse, par visée d’étoiles vues près du contour du Soleil.
Si l’énergie protéiforme est pesante, elle obéit à la loi de la gravitation universelle dans les conditions de localisation que celle-ci suppose, en sorte que :
Deux énergies et localisées sous n’importe quelle forme par rapport à un référentiel de Galilée s’attirent en raison inverse du carré de leur distance et proportionnellement à leurs quantités.
Cette attraction newtonienne vérifie donc l’équation :
où est la constante de gravitation, c’est-à-dire :
avec égal à environ .
54. Matière et photons formes de l’énergie. — Nous voici amenés à penser que toute matière est en définitive une forme particulière très condensée de l’énergie. Nous n’avons plus alors à nous étonner que (V, 37) les forces de gravitation soient exactement proportionnelles aux masses : si une bille d’acier et une bille d’ivoire ont mêmes inerties, c’est qu’elles contiennent la même quantité d’énergie, et nous étions par là justifiés à dire qu’elles contiennent la même quantité de matière (V, 17).
Le Photon constitue une autre forme condensée de l’Énergie. Il est bien remarquable que, sous la forme matière, l’énergie ne peut atteindre la vitesse qu’elle a nécessairement sous la forme photons.
Dire que Matière et Lumière sont deux formes de l’Énergie suggère la possibilité de transformation réciproque de Matière en Lumière et de Lumière en Matière.
En nous penchant « à la surface des choses », nous avons
deviné aux profondeurs la réalité essentielle Énergie.
TABLE DES MATIÈRES
- ↑ À la Surface des Choses, IV, Forces et Travail.
- ↑ Comme nous comprendrons bientôt, cela signifie que, de deux corps inégalement chauds, le plus chaud est celui qui cède de « l’énergie » à l’autre.
- ↑ Joule a montré que, en fait, un léger changement extérieur se produit. Mais la loi est très approchée, comme celle de Mariotte.
- ↑ Par exemple en faisant passer dans le fil un courant qui le volatilise brusquement.
- ↑ Le travail qui serait nécessaire pour communiquer aux poids la vitesse qu’ils prennent dans l’expérience, est en général inférieur au millième du travail dépensé. La correction relative aux échauffements qui se produisent autour des axes non plongés dans le calorimètre est plus importante. On peut mesurer ensemble ces deux corrections comme il suit :
Après avoir déclaveté l’axe qui solidarisait l’agitateur au tambour, on enroule en sens contraire les cordons tenseurs sur ce tambour, de façon que les poids s’équilibrent. L’un de ces poids étant à son niveau inférieur et l’autre à son niveau supérieur, on détermine le mouvement par une petite surcharge telle que la vitesse, bientôt rendue uniforme par les frottements sur les axes, soit ce qu’elle était dans la première expérience : l’abaissement du poids additionnel mesure le faible changement correspondant, que l’on ajoutera à celui trouvé dans le calorimètre.
- ↑ Démonstration inédite, exposée oralement au Collège de France, et à la Société de Physique (Strasbourg 1920).























































































































































































































































![{\displaystyle \mathrm {F} (\xi )\equiv {\frac {\mathrm {G_{0}} }{\alpha }}\left(e^{\alpha \xi }-1\right)\equiv {\frac {\mathrm {G_{0}} }{\alpha }}\left[{\left(1-{\frac {v^{2}}{c^{2}}}\right)}^{\alpha }-1\right]=f(v^{2})}](https://wikimedia.org/api/rest_v1/media/math/render/svg/c376b85c70f4f6f757feb5063e071bb0ac0ff976)


![{\displaystyle 2\left[\left(1-{\frac {v^{\,\prime \,2}}{c^{2}}}\right)^{\alpha }-1\right]\left(1-{\frac {v^{2}}{c^{2}}}\right)^{\alpha }}](https://wikimedia.org/api/rest_v1/media/math/render/svg/c10eafe7a69a80344c2ca2b7bad00183b3c9eb9f)
![{\displaystyle \equiv \left(1-{\frac {v_{1}^{\,\prime \prime \,2}}{c^{2}}}\right)^{\alpha }-1+\left[\left(1-{\frac {v_{2}^{\,\prime \prime \,2}}{c^{2}}}\right)^{\alpha }-1\right]-2\left[\left(1-{\frac {v^{2}}{c^{2}}}\right)^{\alpha }-1\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/94f38e842c76c129ac04bd3bcb1f523459392400)










![{\displaystyle {\begin{aligned}\varphi (v^{2})&={\frac {1}{\sqrt {1-{\frac {v^{2}}{c^{2}}}}}}\\f(v^{2})&=-2\mathrm {G_{0}} \left[{\frac {1}{\sqrt {1-{\frac {v^{2}}{c^{2}}}}}}-1\right]\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/6efb83ad2a0057385fda178d58d84b6d7b058fb8)
![{\displaystyle 2\mathrm {G_{0}} \left[\left(1-{\frac {v^{2}}{c^{2}}}\right)^{-1/2}-1\right]=-2\mathrm {G_{0}} \left[{\frac {1}{2}}{\frac {v^{2}}{c^{2}}}+{\frac {3}{8}}\left({\frac {v^{2}}{c^{2}}}\right)^{2}+\ldots \right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/3b2a0b71ec7eddae2d60a95f687741363b412eda)



![{\displaystyle \mathrm {E} =mc^{2}\left[{\frac {1}{\sqrt {1-{\frac {v^{2}}{c^{2}}}}}}-1\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/3be3a0714a79480b414231788dfe9144a560bc28)















![{\displaystyle mc^{2}\left[{\frac {1}{\sqrt {1-\beta ^{2}}}}-1\right]+mc^{2}={\frac {m}{\sqrt {1-\beta ^{2}}}}c^{2}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/6015a0cb595643c84c40467935a01e6e6be8b401)













