Les méthodes nouvelles de la mécanique céleste/Chap.19

Henri Poincaré

Les méthodes nouvelles de la mécanique céleste

Gauthier-Villars et Fils, 1893 (2, p. 315-393).

CHAPITRE XIX.

MÉTHODES DE M. BOHLIN.

---

Méthode de Delaunay.

199.Reprenons les hypothèses et les notations du n^o 125. Nous avons vu que dans l’application de la méthode du n^o 125 il s’introduisait des diviseurs de la forme

$n_{1}^{0}m_{1}+n_{2}^{0}m_{2}+\ldots +n_{n}^{0}m_{n},$

les $m_{i}$ étant des entiers.

Il en résulte que cette méthode devient illusoire quand l’un de ces diviseurs devient très petit.

Parmi les méthodes qui ont été imaginées pour triompher de cette difficulté, celle de Delaunay est la première en date et son exposition facilitera l’intelligence de toutes les autres.

Considérons d’abord un système d’équations canoniques

(1)

${\begin{aligned}{\frac {dx_{i}}{dt}}&={\frac {d\mathrm {F} }{dy_{i}}},&{\frac {dy_{i}}{dt}}&=-{\frac {d\mathrm {F} }{dx_{i}}},\end{aligned}}$

et supposons que $\mathrm {F}$ soit seulement fonction de $x_{1},$ $x_{2},\,\ldots ,$ $x_{n}$ et de

$m_{1}y_{1}+m_{2}y_{2}+\ldots +m_{n}y_{n},$

périodique de période $2\pi$ par rapport à cette dernière quantité. Je suppose que les $m_{i}$ sont des entiers.

L’intégration du système (1) se ramène alors à celle de l’équation aux dérivées partielles

$\mathrm {F} \left({\frac {d\mathrm {S} }{dy_{1}}},{\frac {d\mathrm {S} }{dy_{2}}},\ldots ,{\frac {d\mathrm {S} }{dy_{n}}},\,m_{1}y_{1}\!+\!m_{2}y_{2}\!+\!\ldots \!+\!m_{n}y_{n}\right)=\mathrm {C} ,$

$\mathrm {C}$ étant une constante arbitraire. Or cette intégration est aisée.

Posons, en effet,

$\mathrm {S} =x_{1}^{0}y_{1}+x_{2}^{0}y_{2}+\ldots x_{n}^{0}y_{n}+\varphi (m_{1}y_{1}+m_{2}y_{2}+\ldots +m_{n}y_{n}),$

l’équation deviendra

$\mathrm {F} \left(x_{1}^{0}\!+\!m_{1}\varphi ',\,x_{2}^{0}\!+\!m_{2}\varphi ',\,\ldots ,\,x_{n}^{0}\!+\!m_{n}\varphi ',\,m_{1}y_{1}\!+\!m_{2}y_{2}\!+\!\ldots \!+\!m_{n}y_{n}\right)=\mathrm {C} .$

Résolvons cette équation par rapport à $\varphi ',$ il viendra

$\varphi '{}={}$fonction de ${\textstyle \sum }\,m_{i}y_{i},$ de $x_{1}^{0},\,x_{2}^{0},\,\ldots ,\,x_{n}^{0}$ et de $\mathrm {C} .$

On intégrera cette expression par rapport à ${\textstyle \sum }\,m_{i}y_{i}$ en regardant $\mathrm {C}$ et les $x_{k}^{0}$ comme des constantes, et l’on aura $\varphi$ et par conséquent $\mathrm {S}$ en fonction de ${\textstyle \sum }\,m_{i}y_{i},$ des $x_{k}^{0}$ et de $\mathrm {C} .$

Il est nécessaire d’entrer dans plus de détails et pour cela je vais considérer un cas particulier simple en faisant

${\begin{array}{c}m_{1}=1,\qquad m_{2}=m_{3}=\ldots =m_{n}=0,\\[0.75ex]\mathrm {F} =x_{1}^{2}+\mu \cos y_{1},\end{array}}$

$\mu$ étant très petit.

Notre équation devient

$\left({\frac {d\mathrm {S} }{dy_{i}}}\right)^{2}+\mu \cos y_{1}=\mathrm {C} ,$

d’où

${\frac {d\mathrm {S} }{dy_{i}}}={\sqrt {\mathrm {C} -\mu \cos y_{1}}}.$

Plusieurs cas sont à considérer :

1^o On a

$\mathrm {C} >|\mu |.$

Dans ce cas le radical ${\sqrt {\mathrm {C} -\mu \cos y_{1}}}$ est toujours réel et ne s’annule jamais. Il est susceptible de deux déterminations l’une positive pour toutes les valeurs de $y_{1},$ l’autre négative pour toutes les valeurs de $y_{1}.$ Prenons par exemple la première, elle sera développable suivant les cosinus des multiples de $y_{1}\,;$ de sorte qu’on aura

${\frac {d\mathrm {S} }{dy_{i}}}=x_{1}^{0}+{\textstyle \sum }\,\mathrm {B} _{n}\cos ny_{1}.$

Je mets en évidence le terme tout connu que j’appelle $x_{1}^{0}\,;$ il est clair que $x_{1}^{0}$ est fonction de $\mathrm {C}$ et par conséquent $\mathrm {C}$ de $x_{1}^{0}\,;$ d’autre part, les $\mathrm {B} _{n}$ seront fonctions de $\mathrm {C}$ et par conséquent de $x_{1}^{0}.$

Il vient alors

$\mathrm {S} =x_{1}^{0}y_{1}+{\textstyle \sum }\,{\frac {\mathrm {B} _{n}}{n}}\sin ny_{1},$

ce qui nous donne $\mathrm {S}$ en fonction de $y_{1}$ et de la constante arbitraire $x_{1}^{0}.$

2^o

$-|\mu |<\mathrm {C} <|\mu |.$

Dans ce cas la quantité sous le radical

$\mathrm {C} -\mu \cos y_{1}$

n’est pas toujours positive, et, par conséquent, on ne peut pas donner à $y_{1}$ toutes les valeurs possibles, mais seulement celles pour lesquelles le radical est réel.

On peut introduire une variable auxiliaire $\varepsilon$ en posant, par exemple,

$\mu \cos y_{1}=\mathrm {C} \cos \varepsilon ,$

d’où

${\frac {d\mathrm {S} }{dy_{1}}}={\sqrt {\mathrm {C} }}\sin \varepsilon ,$

ou

${\frac {d\mathrm {S} }{dt}}={\sqrt {\frac {\mu ^{2}-\mathrm {C} ^{2}\cos ^{2}\varepsilon }{\mathrm {C} }}}\cdot$

Comme $\mathrm {C} ^{2}$ est plus petit que $\mu ^{2},$ le radical du second membre est toujours réel et pourra être développé en série trigonométrique sous la forme

${\frac {d\mathrm {S} }{d\varepsilon }}=\mathrm {B} _{0}+{\textstyle \sum }\,\mathrm {B} _{n}\cos n\varepsilon ,$

d’où

$\mathrm {S} =\mathrm {B} _{0}+{\textstyle \sum }\,{\frac {\mathrm {B} _{n}}{n}}\sin n\varepsilon ,$

ce qui nous donne $\mathrm {S}$ en fonction de la variable auxiliaire $\varepsilon$ et de la constante $\mathrm {C} .$

3^o

$\mathrm {C} =|\mu |.$

Soit, par exemple,

$\mu >0,\quad \mathrm {C} =\mu .$

Il vient alors

${\frac {d\mathrm {S} }{dy_{1}}}={\sqrt {\mu }}{\sqrt {1-\cos y_{1}}}={\sqrt {\frac {\mu }{2}}}\sin {\frac {y_{1}}{2}}$

ou

$\mathrm {S} =-{\sqrt {2\mu }}\cos {\frac {y_{1}}{2}}\cdot$

$\mathrm {S}$ est exprimée en fonction de $y_{1},$ et c’est encore une fonction périodique de $y_{1},$ mais la période n’est plus $2\pi ,$ mais $4\pi .$

J’ajoute que si $\mathrm {C} <-|\mu |$ le radical est toujours imaginaire et que, si $\mathrm {C} =-|\mu |,$ il ne cesse de l’être que pour $y_{1}=0.$ On peut éclaircir ce qui précède de deux manières :

1^o D’abord par la considération des fonctions elliptiques.

Nous voyons en effet que

$\mathrm {S} =\int {\sqrt {\mathrm {C} -\mu \cos y_{1}}}\,dy_{1}$

est une intégrale elliptique et que si nous posons

$u=\int {\frac {dy_{1}}{\sqrt {\mathrm {C} -\mu \cos y_{1}}}},$

les expressions

$\sin y_{1},\quad \cos y_{1},\quad {\sqrt {\mathrm {C} -\mu \cos y_{1}}}$

seront des fonctions doublement périodiques de $u.$

Les divers cas que nous avons examinés plus haut correspondent alors aux diverses hypothèses que l’on peut faire au sujet du discriminant des fonctions elliptiques.

2^o Par la Géométrie.

Nous pouvons construire en effet des courbes en adoptant les coordonnées polaires et en prenant pour rayon vecteur $\mathrm {A} +{\frac {d\mathrm {S} }{dy_{1}}},$ $\mathrm {A}$ étant une constante quelconque et pour angle polaire $y_{1}.$ Nous obtenons ainsi une figure telle que celle-ci.

Les courbes en trait plein correspondent à l’hypothèse $\mathrm {C} >|\mu |,$ la courbe en trait pointillé à l’hypothèse

$-|\mu |<\mathrm {C} <|\mu |,$

la courbe en trait mixte — . — . qui a un point double en $\mathrm {B}$ au cas de $\mathrm {C} =|\mu |\,;$ enfin la courbe correspondant à $\mathrm {C} =-|\mu |,$ correspond à un seul point $\mathrm {A} .$

Si l’on avait voulu appliquer au problème que nous venons de
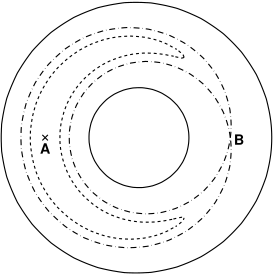
Fig. 2. traiter les méthodes du n^o 125, on aurait été conduit à développer $\mathrm {S}$ suivant les puissances de $\mu .$ Et, en effet, le radical

${\sqrt {\mathrm {C} -\mu \cos y_{1}}}$

est effectivement développable suivant les puissances de $\mu$ et, par conséquent, il en est de même de $\mathrm {S} .$ Seulement le développement n’est convergent que si

$\mathrm {C} <|\mu |.$

Si cette condition n’est pas remplie, les procédés du n^o 125 deviennent illusoires et il faut avoir recours à la méthode de Delaunay, c’est-à-dire à celle que nous venons d’exposer. On peut même y avoir recours avec avantage dès que $\mathrm {C}$ est du même ordre de grandeur que $\mu ,$ parce que la convergence du développement du n^o 125 est alors très lente.

Observons que le développement du radical est de la forme

${\textstyle \sum }\,{\sqrt {\mathrm {C} }}\left({\frac {\mu }{\mathrm {C} }}\right)^{n}\varphi _{n}(y_{1})$

et l’on voit que, si $\mathrm {C}$ est petit, la convergence devient très lente et peut même cesser tout à fait.

Si l’on fait $\mathrm {C} =\mathrm {C} _{1}\mu ,$ le développement devient

${\textstyle \sum }\,{\sqrt {\mathrm {C} _{1}}}{\sqrt {\mu }}\,\varphi _{n}(y_{1}){\frac {1}{\mathrm {C} _{1}^{n}}},$

et tous ses termes sont de même degré en $\mu \,;$ on voit d’ailleurs que

${\sqrt {\mathrm {C} -\mu \cos y_{1}}}={\sqrt {\mu }}{\sqrt {\mathrm {C} _{1}-\cos y_{1}}}.$

200.Passons maintenant à un cas un peu plus général et supposons que $\mathrm {F}$ soit fonction seulement de $x_{1}={\frac {d\mathrm {S} }{dy_{1}}}$ et de $y_{1},$ périodique en $y_{1}.$

L’équation aux dérivées partielles devient

$\mathrm {F} \left({\frac {d\mathrm {S} }{dy_{1}}},y_{1}\right)=\mathrm {C}$

et elle doit être d’abord résolue par rapport à $\mathrm {C} .$

Supposons que l’on ait

$\mathrm {F} =\mathrm {F} _{0}+\mathrm {F} _{1}\mu +\mathrm {F} _{2}\mu ^{2}+\ldots$

et que $\mathrm {F} _{0}$ ne dépende que de ${\frac {d\mathrm {S} }{dy_{1}}}=x_{1}.$

Alors plusieurs cas peuvent se présenter.

Supposons que $\mathrm {F} ,$ qui est déjà développable suivant les puissances de $\mu ,$ soit aussi holomorphe en $x_{1},$ ce qui d’ailleurs arrivera dans toutes les applications.

Alors par les procédés des n^os 30 et suivants, l’équation

(2)

$\mathrm {F} (x_{1},y_{1})=\mathrm {C}$

pourra être résolue par rapport à $x_{1}.$

Pour $\mu =0,$ l’équation s’écrira

(3)

$\mathrm {F} _{0}(x_{1})=\mathrm {C}$ ;

soit $x_{1}^{0}$ une valeur satisfaisant à cette équation (3). Alors, si l’on désigne par $\mathrm {F} _{0}'$ la dérivée de $\mathrm {F} _{0}$ et si

$\mathrm {F} _{0}'(x_{1}^{0})\gtrless 0,$

on tirera de l’équation (2) $x_{1}$ sous la forme d’une série ordonnée suivant les puissances de $\mu ,$ les coefficients étant des fonctions de $y_{1}.$

Si, au contraire,

${\begin{aligned}\mathrm {F} _{0}'(x_{1}^{0})&=0,&\mathrm {F} _{0}''(x_{1}^{0})&\gtrless 0,\end{aligned}}$

on aura encore $x_{1}$ sous la forme d’une série, mais cette série sera développée non pas suivant les puissances de $\mu ,$ mais suivant celles de ${\sqrt {\mu }}.$

Examinons successivement ces deux cas.

Soit d’abord $\mathrm {F} _{0}'(x_{1}^{0})\gtrless 0.$

Nous poserons alors, puisque $x_{1}$ et par conséquent $\mathrm {S}$ sont développables suivant les puissances de $\mu$

$\mathrm {S} =\mathrm {S} _{0}+\mu \,\mathrm {S} _{1}+\mu ^{2}\mathrm {S} _{2}+\ldots$

et nous supposerons d’ailleurs que ${\frac {d\mathrm {S} _{0}}{dy_{1}}}$ se réduit à la constante $x_{1}^{0}\,;$ on calculera ensuite, par récurrence, les autres fonctions $\mathrm {S} _{1},$ $\mathrm {S} _{2},\,\ldots$ et le calcul sera de tout point pareil à celui du n^o 125.

Passons à la seconde hypothèse où $\mathrm {F} _{0}'(x_{1}^{0})=0.$

Alors $\mathrm {S}$ est développable suivant les puissances de ${\sqrt {\mu }}$ et je puis écrire

$\mathrm {S} =\mathrm {S} _{0}+{\sqrt {\mu }}\,\mathrm {S} _{1}+\mu \,\mathrm {S} _{2}+\ldots .$

Je suppose toujours

${\begin{aligned}{\frac {d\mathrm {S} _{0}}{dy_{1}}}&=x_{1}^{0},&\mathrm {S} _{0}&=x_{1}^{0}y_{1}.\end{aligned}}$

J’ai alors

${\begin{aligned}\mathrm {F} _{0}\left({\frac {d\mathrm {S} }{dy_{1}}}\right)=\mathrm {F} _{0}&+{\frac {\mathrm {F} _{0}''}{2}}\left({\sqrt {\mu }}\,{\frac {d\mathrm {S} _{1}}{dy_{1}}}+\mu \,{\frac {d\mathrm {S} _{2}}{dy_{1}}}+\ldots \right)^{2}\\&+{\frac {\mathrm {F} _{0}'''}{2}}\left({\sqrt {\mu }}\,{\frac {d\mathrm {S} _{1}}{dy_{1}}}+\ldots \right)^{3}+\ldots .\end{aligned}}$

Dans le second membre je suppose que dans $\mathrm {F} _{0},$ $\mathrm {F} _{0}'',$ $\mathrm {F} _{0}''',\,\ldots$ on a remplacé $x_{1}$ par $x_{1}^{0}.$

Posons de même

$\mathrm {C} =\mathrm {C} _{0}+\mathrm {C} _{1}{\sqrt {\mu }}+\mathrm {C} _{2}\,\mu +\ldots ,$

en mettant ainsi en évidence que la constante du second membre peut dépendre de $\mu .$

Alors, en égalant dans les deux membres de

$\mathrm {F} =\mathrm {C}$

les coefficients des puissances semblables de $\mu ,$ il viendra

(4)

$\left\{{\begin{aligned}\mathrm {F} _{0}&=\mathrm {C} _{0},\\0&=\mathrm {C} _{1},\\[0.5ex]{\frac {1}{2}}\mathrm {F} _{0}''\left({\frac {d\mathrm {S} _{1}}{dy_{1}}}\right)^{2}&=-\mathrm {F} _{1}(x_{1}^{0},y_{1})+\mathrm {C} _{2},\\[0.5ex]\mathrm {F} _{0}''\,{\frac {d\mathrm {S} _{1}}{dy_{1}}}{\frac {d\mathrm {S} _{2}}{dy_{1}}}&=\Phi +\mathrm {C} _{3},\\[0.5ex]\mathrm {F} _{0}''\,{\frac {d\mathrm {S} _{1}}{dy_{1}}}{\frac {d\mathrm {S} _{3}}{dy_{1}}}&=\Phi +\mathrm {C} _{4},\\[0.5ex]\ldots \ldots \ldots \ldots &\ldots \ldots \ldots ..\end{aligned}}\right.$

Dans la troisième équation (4), je suppose $\mathrm {S} _{0}$ connu ; dans la quatrième, je suppose $\mathrm {S} _{1}$ connu ; dans la cinquième, je suppose connus $\mathrm {S} _{o},$ $\mathrm {S} _{1},$ $\mathrm {S} _{2}$ et ainsi de suite.

Je désigne toujours par $\Phi$ toute fonction connue.

La troisième équation (4) va nous permettre de calculer ${\frac {d\mathrm {S} _{1}}{dy_{1}}},$ car $\mathrm {F} _{0}''$ étant une constante, il vient

${\frac {d\mathrm {S} _{1}}{dy_{1}}}={\sqrt {{\frac {2}{\mathrm {F} _{0}''}}\left[\mathrm {C} _{2}-\mathrm {F} _{1}(x_{1}^{0},y_{1})\right]}}.$

Plusieurs circonstances peuvent se présenter correspondant aux divers cas traités dans l’exemple plus simple dont nous nous sommes occupés plus haut.

Il peut arriver que $\mathrm {C} _{2}$ reste plus grand que $\mathrm {F} _{1}$ quelle que soit la valeur attribuée à $y_{1}\,;$ alors ${\frac {d\mathrm {S} _{1}}{dy_{1}}}$ est une fonction périodique de $y_{1}$ dont la période est $2\pi .$

Ou bien il peut arriver que la condition

$\mathrm {C} _{2}>\mathrm {F} _{1}$

ne soit remplie que pour certaines valeurs de $y_{1}.$ Alors la fonction $\mathrm {S} _{1}$ n’est non plus réelle que pour certaines valeurs de $y_{1}.$

Une fois $\mathrm {S} _{1}$ déterminé,, la quatrième équation (4) nous fera connaître $\mathrm {S} _{2},$ la cinquième $\mathrm {S} _{3}$ et ainsi de suite.

La solution est entièrement satisfaisante dans le premier cas, celui où $\mathrm {S} _{1}$ est toujours réel. Mais, dans le cas contraire, il importe de faire attention à une chose.

Les valeurs de $y_{1}$ pour lesquelles les diverses fonctions $\mathrm {S} _{1}$ $\mathrm {S} _{2},$ $\mathrm {S} _{3},,\,\ldots$ passent du réel à l’imaginaire sont données par l’équation

$\mathrm {C} _{2}=\mathrm {F} _{1}\left(x_{1}^{0},y_{1}\right).$

On pourrait croire alors que c’est pour ces mêmes valeurs que $\mathrm {S}$ passe du réel à l’imaginaire. Cela n’est pas exact ; les valeurs pour lesquelles $\mathrm {S}$ passe du réel à l’imaginaire sont données par les équations

${\begin{aligned}\mathrm {F} &=\mathrm {C} _{0}+\mathrm {C} _{2}\,\mu +\mathrm {C} _{3}\,\mu \,{\sqrt {\mu }}+\ldots ,&{\frac {d\mathrm {F} }{dx_{1}}}&=0.\end{aligned}}$

Elles sont à la vérité fort voisines des premières si $\mu$ est très petit, mais elles ne leur sont pas identiques.

Pour tourner cette difficulté, il y a plusieurs moyens. On peut, par exemple, puisque $\mathrm {C} _{2},$ $\mathrm {C} _{3},\,\ldots$ sont arbitraires, faire $\mathrm {C} _{3}=0$ ainsi que tous les autres $\mathrm {C}$ d’indice impair.

Nous calculerons ensuite successivement

$\mathrm {S} _{1},\quad \mathrm {S} _{2},\quad \mathrm {S} _{3},\quad \ldots ,$

et nous aurons

${\frac {d\mathrm {S} }{dy_{1}}}={\frac {d\mathrm {S} _{0}}{dy_{1}}}+{\frac {d\mathrm {S} _{1}}{dy_{1}}}\,{\sqrt {\mu }}+{\frac {d\mathrm {S} _{2}}{dy_{1}}}\,\mu +{\frac {d\mathrm {S} _{3}}{dy_{1}}}\,\mu \,{\sqrt {\mu }}+\ldots ;$

Comme rien ne distingue ${\sqrt {\mu }}$ de $-{\sqrt {\mu }},$ nous aurons encore une solution en faisant

${\frac {d\mathrm {S} }{dy_{1}}}={\frac {d\mathrm {S} _{0}}{dy_{1}}}-{\frac {d\mathrm {S} _{1}}{dy_{1}}}\,{\sqrt {\mu }}+{\frac {d\mathrm {S} _{2}}{dy_{1}}}\,\mu -{\frac {d\mathrm {S} _{3}}{dy_{1}}}\,\mu \,{\sqrt {\mu }}+\ldots ;$

ces deux solutions sont ou toutes deux réelles ou imaginaires conjuguées. Il en résulte que

$\mathrm {S} _{0},\quad \mathrm {S} _{2},\quad \mathrm {S} _{4},\quad \ldots$

sont toujours réels.

De plus, l’expression

(5)

${\frac {d\mathrm {S} _{1}}{dy_{1}}}+\mu \,{\frac {d\mathrm {S} _{3}}{dy_{1}}}+\mu ^{2}\,{\frac {d\mathrm {S} _{5}}{dy_{1}}}+\ldots$

est toujours réelle ou purement imaginaire et il en résulte que, pour obtenir l’équation qui donne les valeurs de $y_{1}$ pour lesquelles $\mathrm {S}$ passe du réel à l’imaginaire, il suffit d’égaler à zéro l’expression (5).

Comment maintenant se fait le passage du cas où $\mathrm {S}$ est toujours réel au cas où $\mathrm {S}$ est tantôt réel et tantôt imaginaire ?

On s’en rendra mieux compte en construisant la figure suivante analogue à la fig. 2.

Nous prenons pour rayon vecteur ${\frac {d\mathrm {S} }{dy_{1}}}$ et pour angle polaire $y_{1}$ et nous construisons les courbes

$\mathrm {F} \left({\frac {d\mathrm {S} }{dy_{1}}},y_{1}\right)=\mathrm {C} ,$

ou du moins celles d’entre elles pour lesquelles ${\frac {d\mathrm {S} }{dy_{1}}}$ diffère peu de $x_{1}^{0}.$

Ces courbes différeront très peu de celles où le rayon vecteur est égal à

$x_{1}^{0}+{\sqrt {\mu }}\,{\frac {d\mathrm {S} _{1}}{dy_{1}}},$

et où ${\frac {d\mathrm {S} _{1}}{dy_{1}}}$ est donné par la formule

${\sqrt {{\frac {2}{\mathrm {F} _{0}''}}\left(\mathrm {C} _{2}-\mathrm {F} _{1}\right)}}.$

Pour construire ces courbes, il faut faire une hypothèse sur la façon dont varie la fonction $\mathrm {F} _{1}$ quand $y_{1}$ varie de $0$ à $2\pi .$ Supposons par exemple que $\mathrm {F} _{1}$ passe par un maximum, puis par un minimum, puis par un maximum plus grand que le premier, puis par un minimum plus petit que le premier ; nous obtiendrons une figure telle que celle-ci :

On voit que, quand $\mathrm {C} _{2}$ diminue, on obtient successivement :

Si $\mathrm {C} _{2}$ est plus grand que le plus grand maximum, deux courbes concentriques représentées sur la figure en trait pointillé − − − −

Si $\mathrm {C} _{2}$ égale le grand maximum, une courbe à point double représentée en trait plein.

Fig. 3.

Si $\mathrm {C} _{2}$ est compris entre les deux maxima, une courbe analogue à celle qui est représentée en trait mixte — . — .

Si $\mathrm {C} _{2}$ égale le petit maximum, une courbe à point double représentée en trait ponctué . . . . . .

Quand $\mathrm {C} _{2}$ devient plus petit que le plus petit maximum, cette courbe se décompose en deux autres qui sont représentées par le trait + + + + ; l’une de ces courbes se réduit à un point, puis disparaît quand $\mathrm {C} _{2}$ devient égal au plus grand minimum ; l’autre se réduit à un point et disparaît à son tour quand $\mathrm {C} _{2}$ devient égal au plus petit minimum.

On voit que le passage d’un cas à l’autre se fait par une courbe à point double, ce qui conduit à étudier ces courbes et plus particulièrement la première, celle qui est représentée en trait plein.

Si nous supposons un mobile parcourant cette courbe d’un mouvement continu, il partira par exemple du point double, fera le tour d’une des boucles de la courbe, reviendra au point double, parcourra la seconde boucle et reviendra enfin à son point de départ ; on voit que son mouvement est encore périodique, mais que la période est doublée ; de sorte que ${\frac {d\mathrm {S} }{dy_{1}}}$ est une fonction périodique de $y_{1},$ mais que la période est devenue $4\pi$ et n’est plus $2\pi .$

Revenons alors aux équations (4).

Nous trouvons alors que si l’on donne à $\mathrm {C} _{2}$ la valeur qui correspond au maximum de $\mathrm {F} _{1},$ le radical

${\sqrt {{\frac {2}{\mathrm {F} _{0}''}}\left(\mathrm {C} _{2}-\mathrm {F} _{1}\right)}},$

qui est égal à ${\frac {d\mathrm {S} _{1}}{dy_{1}}},$ est une fonction périodique de $y_{1}$ de période $4\pi$ et est par conséquent développable suivant les sinus et les cosinus des multiples de ${\frac {y_{1}}{2}}\cdot$

Quand $y_{1}$ augmente de $2\pi ,$ le radical change de signe, de sorte que le développement ne doit contenir que des multiples impairs de ${\frac {y_{1}}{2}}\cdot$ La fonction s’annule deux fois.

Si en effet $y_{1}^{0}$ est la valeur de $y_{1}$ qui correspond au maximum de $\mathrm {F} _{1},$ la fonction ${\frac {d\mathrm {S} _{1}}{dy_{1}}}$ s’annulera pour $y_{1}=y_{1}^{0}$ et pour $y1=y_{1}^{0}+2\pi .$ Alors, quelles que soient les constantes $\mathrm {C} _{3},$ $\mathrm {C} _{4},\,\ldots ,$ les équations (4) nous montrent que

${\frac {d\mathrm {S} _{2}}{dy_{1}}},\quad {\frac {d\mathrm {S} _{3}}{dy_{1}}},\quad \ldots$

seront des fonctions périodiques de $y_{1}$ de période $2\pi \,;$ seulement ces fonctions pourront devenir infinies pour

$y_{1}=y_{1}^{0}$ou$y_{1}=y_{1}^{0}+2\pi .$

Nous savons toutefois que nous pouvons choisir les constantes $\mathrm {C} _{3},\,\ldots$ de façon que cette circonstance ne se produise pas ; l’existence de la courbe en trait plein de la fig. 3 le prouve suffisamment ; voyons maintenant comment doit se faire ce choix.

Si nous supposons que les constantes d’indice impair

$\mathrm {C} _{3},\quad \mathrm {C} _{5},\quad \ldots ,$

sont nulles, les équations (4) ne changeront pas quand on changera ${\sqrt {\mu }}$ en ${\sqrt {-\mu }}$.

Il en résulte que si la fonction

${\frac {d\mathrm {S} _{0}}{dy_{1}}}+{\sqrt {\mu }}\,{\frac {d\mathrm {S} _{1}}{dy_{1}}}+\mu \,{\frac {d\mathrm {S} _{2}}{dy_{1}}}+\mu \,{\sqrt {\mu }}\,{\frac {d\mathrm {S} _{3}}{dy_{1}}}+\ldots$

satisfait à notre équation, il en sera de même de la fonction

${\frac {d\mathrm {S} _{0}}{dy_{1}}}-{\sqrt {\mu }}\,{\frac {d\mathrm {S} _{1}}{dy_{1}}}+\mu \,{\frac {d\mathrm {S} _{2}}{dy_{1}}}-\mu \,{\sqrt {\mu }}\,{\frac {d\mathrm {S} _{3}}{dy_{1}}}+\ldots .$

Ce sont là les deux solutions des équations (4) et on voit que l’on passe de l’une à l’autre en changeant ${\sqrt {\mu }}$ en $-{\sqrt {\mu }}.$ Mais les équations (4) ne changent pas non plus quand on change $y_{1}$ en $y_{1}+2\pi .$ On passera donc aussi d’une solution à l’autre en changeant $y_{1}$ en $y_{1}+2\pi .$

D’où cette conséquence :

Quand on change $y_{1}$ en $y_{1}+2\pi ,$ les fonctions d’indice pair ${\frac {d\mathrm {S} _{2n}}{dy_{1}}}$ ne changent pas et les fonctions d’indice impair ${\frac {d\mathrm {S} _{2n+1}}{dy_{1}}}$ changent de signe.

Seulement comme ${\frac {d\mathrm {S} _{1}}{dy_{1}}}$ s’annule pour $y_{1}=y_{1}^{0}$ et pour

$y_{1}=y_{1}^{0}+2\pi$

et comme cette dérivée entre en facteur dans le premier membre des équations (4), il pourrait se faire que

${\frac {d\mathrm {S} _{2}}{dy_{1}}},\quad {\frac {d\mathrm {S} _{3}}{dy_{1}}},\quad \ldots$

devinssent infinis pour $y_{1}=y_{1}^{0}+2k\pi ,$ et c’est ce qui arriverait en effet si les constantes $\mathrm {C} _{1},\,\ldots$ n’étaient pas convenablement choisies.

Mais il est possible de faire ce choix de telle façon que les fonctions ${\frac {d\mathrm {S} _{p}}{dy_{1}}}$ restent toujours finies.

Pour le démontrer considérons l’équation

$\mathrm {F} \left({\frac {d\mathrm {S} }{dy_{1}}},y_{1}\right)=\mathrm {C} ,$

que je puis écrire

$\mathrm {F} (x_{1},y_{1})=\mathrm {C} .$

Cette équation, en regardant $x_{1}$ et $y_{1}$ comme les coordonnées d’un

point, représente une courbe. Écrivons que cette courbe a un point

double ; il viendra

${\frac {d\mathrm {F} }{dx_{1}}}={\frac {d\mathrm {F} }{dy_{1}}}=0,$

ce que je puis écrire encore

(5)

$\left\{{\begin{aligned}{\frac {d\mathrm {F} _{0}}{dx_{1}}}+\mu \,{\frac {d\mathrm {F} _{1}}{dx_{1}}}+\mu ^{2}{\frac {d\mathrm {F} _{2}}{dx_{1}}}+\ldots =0,\\[0.75ex]{\frac {d\mathrm {F} _{1}}{dy_{1}}}+\mu \,{\frac {d\mathrm {F} _{2}}{dy_{1}}}+\mu ^{2}{\frac {d\mathrm {F} _{3}}{dy_{1}}}+\ldots =0,\end{aligned}}\right.$

puisque $\mathrm {F} _{0}$ ne dépend pas de $y_{1}.$

Résolvons ces équations (5) par rapport à $x_{1}$ et à $y_{1}.$ Pour $\mu =0$ on trouvera

${\begin{aligned}x_{1}&=x_{1}^{0},&y_{1}&=y_{1}^{0}.\end{aligned}}$

Le déterminant fonctionnel des équations (5) pour $\mu =0,$ $x_{1}=x_{1}^{0},$ $y_{1}=y_{1}^{0}$ s’écrit

${\frac {d^{2}\mathrm {F} _{0}}{dx_{1}^{2}}}{\frac {d^{2}\mathrm {F} _{1}}{dy_{1}^{2}}}$

et, en général, il n’est pas nul. On pourra donc résoudre les équations (5) et l’on trouvera que $x_{1}$ et $y_{1}$ sont développables suivant les puissances de $\mu .$ Soient alors

$x_{1}=\alpha ,\qquad y_{1}=\beta ,$

les développements ainsi obtenus ; l’expression

$\mathrm {F} (\alpha ,\beta )$

est évidemment développable suivant les puissances de $\mu .$ Soit alors

(6)

$\mathrm {F} (\alpha ,\beta )=\mathrm {C} _{0}+\mathrm {C} _{2}\mu +\mathrm {C} _{4}\mu ^{2}+\ldots$

ce développement. Je dis que, si l’on donne dans les équations (4) aux constantes $\mathrm {C} _{2p}$ les valeurs tirées du développement (6), les fonctions ${\frac {d\mathrm {S} _{p}}{dy_{1}}}$ resteront finies.

Pour nous en rendre compte, posons

${\begin{aligned}x_{1}&=\alpha +x',&y_{1}&=\beta +y',\end{aligned}}$

$\mathrm {F} (x_{1},y_{1})=\mathrm {F} (\alpha ,\beta )+\mathrm {F} '$

et envisageons l’équation

$\mathrm {F} '(x',y')=0\,;$

elle est de même forme que l’équation (2) ; nous pouvons donc la traiter de la même manière, c’est-à-dire poser

$x'={\frac {d\mathrm {S} _{0}'}{dy'}}+{\sqrt {\mu }}\,{\frac {d\mathrm {S} _{1}'}{dy'}}+\ldots$

et déterminer les fonctions ${\frac {d\mathrm {S} _{p}'}{dy'}}$ par des équations (4 bis) analogues aux équations (4), et qui n’en différeront que parce que les lettres seront accentuées ; seulement les constantes $\mathrm {C} _{p}$ seront toutes nulles, et pour

$x'=y'=0$

on aura

$\mathrm {F} '={\frac {d\mathrm {F} '}{dx'}}={\frac {d\mathrm {F} '}{dy'}}=0.$

Donc, si l’on regarde $\mathrm {F} '$ comme développé suivant les puissances de $x'$ et $y',$ le développement commencera par des termes du second degré en $x'$ et $y',$ et cela quel que soit $\mu .$ Le développement de $\mathrm {F} _{0}',$ $\mathrm {F} _{1}',\,\ldots$ commencera donc aussi par des termes du second degré. Il résulte de là que, si l’on considère les fonctions $\Phi$ qui figurent dans le second membre des équations (4 bis) comme développées dans le voisinage de $y'=$ 0, suivant les puissances de $y'$ et des ${\frac {d\mathrm {S} _{p}'}{dy'}},$ le développement commencera toujours par des termes du second degré.

On voit d’abord que ${\frac {d\mathrm {S} _{1}'}{dy'}}$ s’annule pour $y'=0\,;$ on pourrait donc craindre que ${\frac {d\mathrm {S} _{p}'}{dy'}}$ ne devienne infini pour $y'=0\,;$ mais, loin de là, je dis que, pour cette valeur de $y',$ ${\frac {d\mathrm {S} '_{p}}{dy'}}$ est nul.

En effet, supposons que cela soit vrai pour

${\frac {d\mathrm {S} _{1}'}{dy'}},\quad {\frac {d\mathrm {S} _{2}'}{dy'}},\quad \ldots ,\quad {\frac {d\mathrm {S} _{p-1}'}{dy'}}$

je dis que cela sera vrai également pour ${\frac {d\mathrm {S} _{p}'}{dy'}}\cdot$

Considérons l’équation

$\mathrm {F} _{0}''\,{\frac {d\mathrm {S} _{1}'}{dy'}}\,{\frac {d\mathrm {S} _{p}'}{dy'}}=\Phi ,$

où $\mathrm {F} _{0}''$ désigne la dérivée seconde de $\mathrm {F} _{0}'.$ $\Phi$ est développé suivant les puissances de $y',$ de ${\frac {d\mathrm {S} _{1}'}{dy'}},\,\ldots ,$ ${\frac {d\mathrm {S} _{p-1}'}{dy'}}\,;$ comme $y'=0$ est un zéro simple pour ces diverses quantités, et que le développement de $\Phi$ commence par des termes du second degré, $y'=0$ sera un zéro double pour $\Phi .$

Ce sera un zéro simple pour ${\frac {d\mathrm {S} _{1}'}{dy'}}\cdot$

Ce sera donc un zéro simple pour ${\frac {d\mathrm {S} _{p}'}{dy'}}\cdot$

C.Q.F.D.

Nous trouvons ainsi

$x'={\frac {d\mathrm {S} '}{dy'}},$

$\mathrm {S} '=\mathrm {S} _{0}'+{\sqrt {\mu }}\,\mathrm {S} _{1}'+\mu \,\mathrm {S} _{2}'+\ldots ,\quad \mathrm {S} _{0}'=0.$

Nous en déduisons

(7)

$x_{1}=\alpha +{\frac {d\mathrm {S} '(y_{1}-\beta )}{dy_{1}}}\cdot$

$\mathrm {S} '(y_{1}-\beta )$ représente la fonction $\mathrm {S} ',$ où l’argument $y'$ a été remplacé par l’argument $y_{1}-\beta .$ Soient

${\begin{alignedat}{5}\alpha &=\alpha _{0}&{}+{}&\mu \,\alpha _{1}&{}+{}&\mu ^{2}\alpha _{2}&{}+{}&\ldots ,\\\beta &=\beta _{0}&{}+{}&\mu \,\beta _{1}&{}+{}&\mu ^{2}\beta _{2}&{}+{}&\ldots ,\end{alignedat}}$

$x_{1}={\frac {d\mathrm {S} _{0}}{dy_{1}}}+{\sqrt {\mu }}\,{\frac {d\mathrm {S} _{1}}{dy_{1}}}+\ldots$

les développements de $\alpha ,$ $\beta$ et $x_{1},$ il viendra en identifiant les deux membres de (7)

(8)

$\;\left\{{\begin{array}{c}{\dfrac {d\mathrm {S} _{0}}{dy_{1}}}=\alpha _{0},\qquad {\dfrac {d\mathrm {S} _{1}}{dy_{1}}}={\dfrac {d\mathrm {S} _{1}'(y_{1}-\beta _{0})}{dy_{1}}},\qquad {\dfrac {d\mathrm {S} _{2}}{dy_{1}}}=\alpha _{1}+{\dfrac {d\mathrm {S} _{2}'}{dy_{1}}},\\[0.75ex]{\dfrac {d\mathrm {S} _{3}}{dy_{1}}}={\dfrac {d\mathrm {S} _{3}'}{dy_{1}}}-\beta _{1}\,{\dfrac {d^{2}\mathrm {S} _{1}'}{dy_{1}^{2}}},\qquad {\dfrac {d\mathrm {S} _{4}}{dy_{1}}}=\alpha _{2}+{\dfrac {d\mathrm {S} _{4}'}{dy_{1}}}-\beta _{1}\,{\dfrac {d^{2}\mathrm {S} _{2}'}{dy_{1}^{2}}},\quad \ldots .\end{array}}\right.$

Dans les dérivées des $\mathrm {S} _{p}',$ $y'$ doit être remplacé par l’argument $y_{1}-\beta _{0}.$

On voit que les ${\frac {d\mathrm {S} _{p}}{dy_{1}}}$ restent finis.

Une fois qu’on a démontré la possibilité de déterminer les constantes $\mathrm {C} _{p}$ de façon à éviter que les ${\frac {d\mathrm {S} _{p}}{dy_{1}}}$ deviennent infinis, on peut faire effectivement cette détermination sans avoir besoin de chercher les développements de $\alpha$ et de $\beta .$

Il suffit de se servir des équations (4).

Considérons l’une de ces équations ;

$\mathrm {F} _{0}''\,{\frac {d\mathrm {S} _{1}}{dy_{1}}}\,{\frac {d\mathrm {S} _{p-1}}{dy_{1}}}=\Phi +\mathrm {C} _{p}.$

Si $p$ est pair, on prendra

$\mathrm {C} _{p}=-\Phi (y_{1}^{0}),$

et, comme $\Phi$ est une fonction périodique de période $2\pi ,$ on aura également

$\mathrm {C} _{p}=-\Phi (y_{1}^{0}+2\pi ),$

de sorte que ${\frac {d\mathrm {S} _{p-1}}{dy_{1}}}$ ne deviendra infini ni pour $y_{1}=y_{1}^{0},$ ni pour $y_{1}=y_{1}^{0}+2\pi .$

Si $p$ est impair, il faut faire $\mathrm {C} _{p}=0,$ et la condition

$\Phi (y_{1}^{0})=0$

${\big [}$qui entraîne la suivante

$\Phi (y_{1}^{0}+2\pi )=0$

puisque $\Phi$ change de signe quand $y_{1}$ augmente de $2\pi {\big ]}$ sera remplie d’elle-même.

Il en résultera encore que ${\frac {d\mathrm {S} _{p-1}}{dy_{1}}}$ ne devient jamais infini.

Il en résulte enfin que ${\frac {d\mathrm {S} _{p}}{dy_{1}}}$ est développable suivant les sinus et cosinus des multiples de $y_{1}$ si $p$ est pair et suivant les sinus et cosinus des multiples impairs de ${\frac {y_{1}}{2}}$ si $p$ est impair.

J’ai beaucoup insisté sur des choses presque évidentes, parce que j’aurai plus loin à traiter un problème analogue, mais beaucoup plus difficile, et que je tenais à faire ressortir les analogies.

201.Voyons maintenant comment se fait le passage du premier cas, celui où

$\mathrm {F} _{0}'(x_{1}^{0})\gtrless 0$

et où les procédés du n^o 125 sont applicables au second cas où

$\mathrm {F} _{0}'(x_{1}^{0})=0$

et que nous venons d’étudier en détail.

Observons d’abord que $\mathrm {F} _{0}'(x_{1}^{0})$ est ce que nous avons appelé $-n_{1}^{0}$ au n^o 125 et dans d’autres parties de cet Ouvrage. Alors, en posant

${\frac {d\mathrm {S} }{dy_{1}}}={\frac {d\mathrm {S} _{0}}{dy_{1}}}+\mu \,{\frac {d\mathrm {S} _{1}}{dy_{1}}}+\mu ^{2}{\frac {d\mathrm {S} _{2}}{dy_{1}}}+\ldots ,$

on trouve une série d’équations de la forme

(1)

$n_{1}^{0}\,{\frac {d\mathrm {S} _{p}}{dy_{1}}}=\Phi +\mathrm {C} _{p}.$

On peut, comme je l’ai expliqué au n^o 125, déterminer $\mathrm {C} _{p}$ arbitrairement ; je supposerai qu’on le fasse de telle sorte que la valeur moyenne de $\Phi +\mathrm {C} _{p}$ soit nulle, et par conséquent que $\mathrm {S} _{p}$ soit une fonction périodique de $y_{1}.$

On voit que dans le développement de ${\frac {d\mathrm {S} _{p}}{dy_{1}}}$ différentes puissances de $n_{1}^{0}$ entreront au dénominateur, de sorte que, si $n_{1}^{0}$ est petit, certains termes de ${\frac {d\mathrm {S} _{p}}{dy_{1}}}$ pourront devenir sensibles. Il importe avant tout de se rendre compte de l’exposant maximum que peut avoir $n_{1}^{0}$ dans le dénominateur des divers termes de ${\frac {d\mathrm {S} _{p}}{dy_{1}}}\cdot$

Je dis que cet exposant maximum est égal à $2p-1.$

En effet, $\mathrm {S}$ est une fonction de $y_{1}$ d’une part, et d’autre part du paramètre $\mu$ et de la constante d’intégration $x_{1}^{0}\,;$ je ne parle pas des constantes $\mathrm {C} _{p}$ qui sont entièrement déterminées par les conditions

$\mathrm {F} _{0}(x_{1}^{0})=\mathrm {C} _{0}0,$

valeur moyenne de

$(\Phi +\mathrm {C} _{p})=0.$

Au lieu de $x_{1}^{0}$ nous pouvons prendre pour constante d’intégration $n_{1}^{0}\,;$ alors $\mathrm {S}$ sera fonction de $y_{1},$ de $\mu$ et de $n_{1}^{0}\,;$ développons-la suivant les puissances de $\mu$ et de $n_{1}^{0}\,;$ le développement contiendra des puissances négatives de $n_{1}^{0}.$

L’équation

$n_{1}^{0}\,{\frac {d\mathrm {S} _{1}}{dy_{1}}}=\Phi +\mathrm {C} _{1}$

nous montre que le développement de ${\frac {d\mathrm {S} _{1}}{dy_{1}}}$ suivant les puissances croissantes de $n_{1}^{0}$ commencera par un terme en ${\frac {\scriptstyle 1}{n_{1}^{0}}}\cdot$

Passons à l’équation suivante

$n_{1}^{0}\,{\frac {d\mathrm {S} _{2}}{dy_{1}}}=\Phi +\mathrm {C} _{2}\,;$

$\Phi$ dépendra de ${\frac {d\mathrm {S} _{1}}{dy_{1}}}\,;$ mais, comme $\Phi$ s’obtient en remplaçant dans $\mathrm {F}$ la variable $x_{1}={\frac {d\mathrm {S} }{dy_{1}}}$ par le développement

${\frac {d\mathrm {S} _{0}}{dy_{1}}}+\mu \,{\frac {d\mathrm {S} _{1}}{dy_{1}}}+\ldots ,$

et en retenant dans le développement les termes en $\mu ^{2},$ on voit que $\Phi$ ne peut contenir ${\frac {d\mathrm {S} _{1}}{dy_{1}}}$ qu’à la deuxième puissance au plus ; car le cube de ${\frac {d\mathrm {S} _{1}}{dy_{1}}}$ devrait être accompagné du facteur $\mu ^{3}$ et ne pourrait par conséquent donner de terme en $\mu ^{2}.$

Ainsi le développement de $\Phi ,$ et par conséquent celui de $\mathrm {C} _{2},$ commencera par un terme en

$\left({\frac {1}{n_{1}^{0}}}\right)^{2}$

et enfin celui de ${\frac {d\mathrm {S} _{2}}{dy_{1}}}$ par un terme en

$\left({\frac {1}{n_{1}^{0}}}\right)^{3}\cdot$

La loi est manifeste ; le développement de ${\frac {d\mathrm {S} _{p}}{dy_{1}}}$ commence par un terme en

$\left({\frac {1}{n_{1}^{0}}}\right)^{2p-1}\cdot$

Et, en effet, supposons qu’elle soit vraie pour

${\frac {d\mathrm {S} _{1}}{dy_{1}}},\quad {\frac {d\mathrm {S} _{2}}{dy_{1}}},\quad \ldots ,\quad {\frac {d\mathrm {S} _{p-1}}{dy_{1}}},$

je dis qu’elle est encore vraie pour ${\frac {d\mathrm {S} _{p}}{dy_{1}}}\cdot$

Considérons l’équation

$n_{1}^{0}\,{\frac {d\mathrm {S} _{p}}{dy_{1}}}=\Phi +\mathrm {C} _{p}.$

$\Phi$ est un polynôme entier en

${\frac {d\mathrm {S} _{1}}{dy_{1}}},\quad {\frac {d\mathrm {S} _{2}}{dy_{1}}},\quad \ldots ,\quad {\frac {d\mathrm {S} _{p-1}}{dy_{1}}}\cdot$

Considérons un terme quelconque $u$ de ce polynôme et cherchons à évaluer la somme des indices $q$ des divers facteurs de la forme ${\frac {d\mathrm {S} _{q}}{dy_{1}}}$ qui entrent dans $u.$

Ce terme $u$ provenant d’un terme en $\mu ^{p}$ dans le développement de

$\mathrm {F} \left({\frac {d\mathrm {S} _{0}}{dy_{1}}}+\mu \,{\frac {d\mathrm {S} _{1}}{dy_{1}}}+\ldots \right),$

cette somme est au plus égale à $p.$ De plus, si cette somme est égale à $p,$ comme aucun des indices $q$ n’est égal à $p,$ le terme considéré $u$ contiendra au moins deux facteurs.

Le développement de $u$ suivant les puissances de $n_{1}^{0}$ commencera par un terme en

$\left({\frac {1}{n_{1}^{0}}}\right)^{{\textstyle \sum }\,(2q-1)}\cdot$

Or

${\textstyle \sum }\,q\leqq p.$

Si

${\textstyle \sum }\,q<p,$

${\textstyle \sum }\,(2q-1)\leqq 2p-2\,;$

si

${\textstyle \sum }\,q=p,$

on aura encore

${\textstyle \sum }\,(2q-1)\leqq 2p-2\,;$

parce qu’il y aura au moins deux facteurs.

Donc le développement de $\Phi ,$ et par conséquent celui de $C_{p},$ commencera par un terme en

$\left({\frac {1}{n_{1}^{0}}}\right)^{2p-2}$

et celui de ${\frac {d\mathrm {S} _{p}}{dy_{1}}}$ commencera par un terme en

$\left({\frac {1}{n_{1}^{0}}}\right)^{2p-1}\cdot$
C.Q.F.D.

Mais, $n_{1}^{0}$ étant une constante arbitraire, remplaçons-la par un développement quelconque

$n_{1}^{0}=\alpha _{0}+\mu \alpha _{1}+\mu ^{2}\alpha _{2}+\ldots .$

Alors $\mathrm {S}$ sera développé suivant les puissances positives de $\mu ,$ et les puissances positives et négatives de

$\alpha _{0}+\mu \alpha _{1}+\mu ^{2}\alpha _{2}+\ldots .$

Si $\alpha _{0}$ n’est pas nul, ces puissances positives et négatives peuvent elles-mêmes se développer suivant les puissances positives de $\mu ,$ de sorte que finalement $\mathrm {S}$ se trouvera développé suivant les puissances positives de $\mu .$

Ces développements sont, d’après ce que nous avons vu au n^o 125, les mêmes que ceux qu’on obtiendrait en partant des équations (1), mais en attribuant aux constantes $\mathrm {C} _{p}$ d’autres valeurs que celles que nous leur avons données plus haut.

Maintenant, au lieu de cela, supposons $n_{1}^{0}$ très petit et remplaçons $n_{1}^{0}$ par un développement de la forme

(2)

$n_{1}^{0}=\alpha _{1}{\sqrt {\mu }}+\alpha _{2}\mu +\alpha _{3}\mu {\sqrt {\mu }}+\ldots .$

Cette fois les puissances négatives de

$\alpha _{1}{\sqrt {\mu }}+\alpha _{2}\mu +\ldots$

ne sont plus développables suivant les puissances positives de ${\sqrt {\mu }},$ mais

${\frac {\mu ^{p}}{\left(n_{1}^{0}\right)^{2p-1}}}$

sera développable suivant les puissances positives de ${\sqrt {\mu }}$ et le développement commencera par un terme en ${\sqrt {\mu }}.$

Si nous observons maintenant que, d’après ce que nous venons de voir, $\mathrm {S}$ est développable suivant les puissances de

${\frac {\mu }{n_{1}^{0}}},\quad {\frac {\mu ^{2}}{\left(n_{1}^{0}\right)^{3}}},\quad {\frac {\mu ^{p}}{\left(n_{1}^{0}\right)^{2p-1}}},\quad \mu ,\quad n_{1}^{0},$

nous conclurons que $\mathrm {S}$ est développable suivant les puissances positives de ${\sqrt {\mu }}.$

Les développements ainsi obtenus ne diffèrent pas de ceux auxquels nous sommes arrivés dans le numéro précédent à l’aide des équations (4) et en attribuant diverses valeurs aux constantes $\mathrm {C} _{p}.$

Pour éviter toute confusion je représenterai par

(3)

$\mathrm {S} =\mathrm {S} _{0}+\mu \,\mathrm {S} _{1}+\mu ^{2}\,\mathrm {S} _{2}+\ldots$

le développement obtenu en partant des équations (1) où l’on a déterminé les $\mathrm {C} _{p},$ comme je l’ai dit plus haut, de telle façon que la valeur moyenne de $\Phi +\mathrm {C} _{p}$ soit nulle.

Je représenterai pour un instant par

(4)

$\mathrm {S} =\mathrm {T} _{0}+{\sqrt {\mu }}\,\mathrm {T} _{1}+\mu \,\,\mathrm {T} _{2}+\mu {\sqrt {\mu }}\,\mathrm {T} _{3}+\ldots$

celui que l’on obtient en remplaçant dans (3) $n_{1}^{0}$ par son développement (2) et en ordonnant suivant les puissances de ${\sqrt {\mu }}.$

Que représentent alors $\mathrm {T} _{0},\,\mathrm {T} _{1},$ etc. ?

On obtiendra $\mathrm {T} _{0}$ en remplaçant dans $\mathrm {S} _{0}$ la constante $n_{1}^{0}$ par 0.

On obtiendra $\mathrm {T} _{1}$ de la façon suivante. Mettons en évidence ce fait que $\mathrm {S} _{0}$ dépend de $n_{1}^{0}$ en écrivant $\mathrm {S} _{0}(n_{1}^{0})\,;$ nous avons trouvé

${\begin{alignedat}{3}&\mathrm {S} _{0}(n_{1}^{0})&&=x_{1}^{0}y_{1},\\&\mathrm {S} _{0}(0)&&=\mathrm {T} _{0}.\end{alignedat}}$

Il vient

$\mathrm {S} _{0}(n_{1}^{0})=\mathrm {S} _{0}\left(\alpha _{1}{\sqrt {\mu }}+\alpha _{2}\mu +\ldots \right)=\mathrm {T} _{0}+{\frac {d\mathrm {S} _{0}}{dn_{1}^{0}}}{\sqrt {\mu }}\,\alpha _{1}+\ldots$

ou

$\mathrm {S} _{0}(n_{1}^{0})=\mathrm {T} _{0}+\alpha _{1}\,{\frac {dx_{1}^{0}}{dn_{1}^{0}}}\,y_{1}{\sqrt {\mu }}+\ldots =\mathrm {T} _{0}-{\frac {\alpha _{1}{\sqrt {\mu }}}{\mathrm {F} _{0}''}}\,y_{1}+\ldots ,$

$\mathrm {F} _{0}''$ ayant la même signification que dans les équations (4) du numéro précédent.

D’autre part, nous aurons dans $\mathrm {T} _{1}$ des termes provenant de $\mathrm {S} _{1},$ $\mathrm {S} _{2},\,\ldots \,;$ on les obtiendra comme il suit.

Dans le développement (3) nous prendrons tous les termes en

${\frac {\mu ^{p}}{(n_{1}^{0})^{2p-1}}}\cdot$

Soit

(5)

$\mathrm {S} _{1}'\,{\frac {\mu }{n_{1}^{0}}}+\mathrm {S} _{2}'\,{\frac {\mu ^{2}}{(n_{1}^{0})^{3}}}+\mathrm {S} _{3}'\,{\frac {\mu ^{3}}{(n_{1}^{0})^{5}}}+\ldots ,$

l’ensemble de ces termes.

On aura alors

$\mathrm {T} _{1}=-{\frac {\alpha _{1}y_{1}}{\mathrm {F} _{0}''}}+{\frac {\mathrm {S} _{1}'}{\alpha _{1}}}+{\frac {\mathrm {S} _{2}'}{\alpha _{1}^{3}}}+{\frac {\mathrm {S} _{3}'}{\alpha _{1}^{5}}}+\ldots$

Il en résulte que, si l’on groupe dans le développement (3) tous les termes en ${\frac {\mu ^{p}}{(x_{1}^{0})^{2p-1}}},$ c’est-à-dire tous ceux qui appartiennent au développement (5) et qu’on forme le carré de

${\frac {d\mathrm {T} _{1}}{dy_{1}}}=-{\frac {\alpha _{1}}{\mathrm {F} _{0}''}}+{\frac {1}{\alpha _{1}}}{\frac {d\mathrm {S} _{1}'}{dy_{1}}}+{\frac {1}{\alpha _{1}^{3}}}{\frac {d\mathrm {S} _{2}'}{dy_{1}}}+\ldots ,$

ce carré se réduira à deux termes

$\left({\frac {d\mathrm {T} _{1}}{dy_{1}}}\right)^{2}={\frac {\alpha _{1}^{2}}{\mathrm {F} _{0}''^{2}}}-{\frac {2}{\mathrm {F} _{0}''^{2}}}\,{\frac {d\mathrm {S} _{1}'}{dy_{1}}}\cdot$

C’est là un fait d’autant plus remarquable qu’il peut s’étendre, comme nous le verrons bientôt, à toutes les équations de la Dynamique.

Pour obtenir $\mathrm {T} _{2}$ il faudra tenir compte non seulement de $\mathrm {S} _{0}$ et des termes en

${\frac {\mu ^{p}}{(n_{1}^{0})^{2p-1}}},$

mais des termes en

${\frac {\mu ^{p}}{(n_{1}^{0})^{2p-2}}},\quad \ldots .$

En résumé, le passage du cas où les méthodes du n^o 125 sont applicables à celui où elles cessent de l’être se fait de la façon suivante : quand $n_{1}^{0}$ est très petit, l’ordre de grandeur d’un terme ne dépend plus seulement de l’exposant de $\mu ,$ mais de celui de $n_{1}^{0}\,;$ si l’on suppose que $n_{1}^{0}$ est du même ordre que ${\sqrt {\mu }},$ on réunira ensemble les termes qui deviennent ainsi du même ordre et on les sommera.

202.Tous ces résultats s’étendent immédiatement au cas plus général que nous avons considéré au début du n^o 199.

Supposons d’abord que $\mathrm {F}$ dépende de $x_{1},$ $x_{2},\,\ldots ,$ $x_{n}$ et de $y_{1}\,;$ nous aurons alors à envisager l’équation

(1)

$\mathrm {F} \left({\frac {d\mathrm {S} }{dy_{1}}},{\frac {d\mathrm {S} }{dy_{1}}},\ldots ,{\frac {d\mathrm {S} }{dy_{n}}},y_{1}\right)=\mathrm {const.}$

Pour l’intégrer nous donnerons à

${\frac {d\mathrm {S} }{dy_{2}}},\quad \ldots ,\quad {\frac {d\mathrm {S} }{dy_{n}}}$

des valeurs constantes quelconques,

$x_{2}^{0},\quad \ldots ,,\quad x_{n}^{0},$

et nous aurons ainsi une équation

$\mathrm {F} \left({\frac {d\mathrm {S} }{dy_{1}}},\,x_{2}^{0},\,\ldots ,\,x_{n}^{0},\,y_{1}\right)=\mathrm {C} ,$

de même forme que celle dont nous nous sommes occupe dans les deux numéros précédents.

Seulement la solution $\mathrm {S} ,$ au lieu de contenir seulement une constante arbitraire $x_{1}^{0},$ en contiendra $n$ qui seront $x_{1}^{0},$ $x_{2}^{0},\,\ldots ,$ $x_{n}^{0}.$

Si maintenant l’équation fondamentale s’écrit

(2)

$\;\mathrm {F} \left({\frac {d\mathrm {S} }{dy_{1}}},\,{\frac {d\mathrm {S} }{dy_{2}}},\,\ldots ,\,{\frac {d\mathrm {S} }{dy_{n}}},\,m_{1}y_{1}+m_{2}y_{2}+\ldots +m_{n}y_{n}\right)=\mathrm {C} ,$

il est facile de la ramener à la forme (1). Posons en effet

(3)

$\left\{{\begin{aligned}m_{1}y_{1}+m_{2}y_{2}+\ldots +m_{n}y_{n}&=y_{1}',\\m_{1}^{2}y_{1}+m_{2}^{2}y_{2}+\ldots +m_{n}^{2}y_{n}&=y_{2}',\\\ldots \ldots \ldots \ldots \ldots \ldots \ldots \ldots \ldots &\ldots ..,\\m_{1}^{n}y_{1}+m_{2}^{n}y_{2}+\ldots +m_{n}^{n}y_{n}&=y_{n}',\end{aligned}}\right.$

les $m_{i}^{k}$ étant des entiers choisis de telle sorte que le déterminant des coefficients des équations (3) soit égal à 1. Cela est toujours possible, pourvu que $m_{1},$ $m_{2},$ $\ldots ,\,m_{n}$ soient premiers entre eux, ce qu’il est toujours permis de supposer.

L’équation aux dérivées partielles (2) devient alors

$\mathrm {F} \left({\frac {d\mathrm {S} }{dy_{1}}},\,{\frac {d\mathrm {S} }{dy_{2}}},\,\ldots ,\,{\frac {d\mathrm {S} }{dy_{n}}},\,y_{1}'\right)=\mathrm {C} ,$

et elle est ainsi ramenée à la forme (1).

Tout ce que nous avons dit des équations de la forme (1) s’étend donc aux équations de la forme (2).

Nous pouvons trouver des solutions de l’équation (2) qui seront développables comme celles de (1), tantôt suivant les puissances de $\mu ,$ tantôt suivant celles de ${\sqrt {\mu }}.$

Pour $\mu =0,\,\mathrm {S}$ se réduira à

$\mathrm {S} _{0}=x_{1}^{0}y_{1}+x_{2}^{0}y_{2}+\ldots +x_{n}^{0}y_{n}.$

La solution complète de l’équation aux dérivées partielles (2) doit contenir $n$ constantes arbitraires. Nous pourrions prendre comme constantes arbitraires $x_{1}^{0},$ $x_{2}^{0},$ $\ldots ,\,x_{n}^{0}\,;$ ou bien encore $n_{1}^{0},$ $n_{2}^{0},$ $\ldots ,\,n_{n}^{0}$ en posant

$n_{i}^{0}=-{\frac {d\mathrm {F} _{0}}{dx_{i}^{0}}}\cdot$

Mais il est plus commode d’introduire un nombre infini de constantes arbitraires, parmi lesquelles il n’y en aura d’ailleurs que $n$ qui soient distinctes. Ces constantes seront

$n_{1}^{0},\quad n_{2}^{0},\quad \ldots ,\quad \mathrm {C} _{0},\quad \mathrm {C} _{1},\quad \mathrm {C} _{2},\quad \ldots ,\quad \mathrm {C} _{p},\quad \ldots ,$

en égalant le second membre de (2) à

$\mathrm {C} =\mathrm {C} _{0}+\mathrm {C} _{1}\mu +\mathrm {C} _{2}\mu ^{2}+\ldots .$

Si

$m_{1}n_{1}^{0}+m_{2}n_{2}^{0}+\ldots +m_{n}n_{n}^{0}\gtrless 0,$

$\mathrm {S}$ est développable suivant les puissances de $\mu$ et si, au contraire,

$m_{1}n_{1}^{0}+m_{2}n_{2}^{0}+\ldots +m_{n}n_{n}^{0}=0,$

$\mathrm {S}$ est développable suivant les puissances de ${\sqrt {\mu }}.$

Supposons en particulier que, donnant à $n_{1}^{0},$ $n_{2}^{0},$ $\ldots ,\,n_{n}^{0}$ des valeurs quelconques, on choisisse les constantes $\mathrm {C} _{p}$ de telle façon que

$\mathrm {S} -n_{1}^{0}y_{1}-n_{2}^{0}y_{2}-\ldots -n_{n}^{0}y_{n}$

soit une fonction périodique des $y\,;$ on retombera sur un développement qui correspondra à celui que nous avons au début du numéro précédent déduit des équations (1) de ce numéro.

Dans ce développement, diverses puissances de

$m_{1}n_{1}^{0}+m_{2}n_{2}^{0}+\ldots +m_{n}n_{n}^{0},$

entreront au dénominateur.

Remplaçons ensuite les constantes d’intégration $n_{i}^{0}$ par divers développements procédant suivant les puissances de ${\sqrt {\mu }}.$

Soit, par exemple,

$n_{i}^{0}=\alpha _{i}^{0}+{\sqrt {\mu }}\,\alpha _{i}^{1}+\mu \,\alpha _{i}^{2}+\ldots .$

Je suppose que

$m_{1}\alpha _{1}^{0}+m_{2}\alpha _{2}^{0}+\ldots +m_{n}\alpha _{n}^{0}=0.$

Il en résultera que le développement de

$m_{1}n_{1}^{0}+m_{2}n_{2}^{0}+\ldots +m_{n}n_{n}^{0}$

commencera par un terme en ${\sqrt {\mu }}.$

Si nous ordonnons ensuite les termes de $\mathrm {S}$ suivant les puissances positives et croissantes de ${\sqrt {\mu }},$ on obtiendra divers développements analogues à ceux que nous avons étudiés en détail dans le n^o 201.

203.Il est aisé maintenant de comprendre l’esprit de la méthode de Delaunay.

Reprenons le cas général des équations de la Dynamique ; et supposons par conséquent que notre fonction

$\mathrm {F} =\mathrm {F} _{0}+\mu \,\mathrm {F} _{1}+\mu ^{2}\mathrm {F} _{2}+\ldots$

dépend non plus seulement de $m_{1}y_{1}+m_{2}y_{2}+\ldots +m_{n}y_{n},$ mais des $n$ arguments $y_{1},$ $y_{2},$ $\ldots ,\,y_{n}$ et qu’elle est d’ailleurs périodique par rapport à ces arguments.

Si aucune des combinaisons linéaires à coefficients entiers

$m_{1}n_{1}^{0}+m_{2}n_{2}^{0}+\ldots +m_{n}n_{n}^{0}$

n’est très petite, les méthodes du n^o 125 pourront s’appliquer sans difficulté ; mais, si l’une de ces combinaisons est très petite, on distinguera dans $\mathrm {F}$ les termes qui dépendent de l’argument

$m_{1}y_{1}+m_{2}y_{2}+\ldots +m_{n}y_{n}.$

$\mathrm {F}$ est supposé développé en série trigonométrique, c’est-à-dire en une suite de termes dont chacun est le produit de

$\cos(p_{1}y_{1}+p_{2}y_{2}+\ldots +p_{n}y_{n})$

ou de

$\sin(p_{1}y_{1}+p_{2}y_{2}+\ldots +p_{n}y_{n})$

(les $p$ étant des entiers), par un coefficient qui est une fonction de $x_{1},$ $x_{2},$ $\ldots ,\,x_{n}.$

Considérons l’ensemble de ces termes qui sont tels que

${\frac {p_{1}}{m_{1}}}={\frac {p_{2}}{m_{2}}}=\ldots ={\frac {p_{n}}{m_{n}}},$

et soit

$\mathrm {F} '=\mathrm {F} _{0}'+\mu \,\mathrm {F} _{1}'+\ldots$

l’ensemble de ces termes.

Ils comprendront en particulier tous les termes de $\mathrm {F}$ qui sont indépendants de $y_{1},$ $y_{2},$ $\ldots ,\,y_{n}$ et par exemple tous ceux de $\mathrm {F} _{0},$ de sorte qu’on aura

$\mathrm {F} _{0}'=\mathrm {F} _{0}.$

Considérons maintenant l’équation

$\mathrm {F} '\left({\frac {d\mathrm {S} }{dy_{1}}},\,{\frac {d\mathrm {S} }{dy_{2}}},\,\ldots ,\,{\frac {d\mathrm {S} }{dy_{n}}},\,m_{1}y_{1}+m_{2}y_{2}+\ldots +m_{n}y_{n}\right)=\mathrm {C} .$

Nous pourrons l’intégrer facilement par les procédés exposés dans les premiers numéros de ce Chapitre.

Soit

$\mathrm {S} =x_{1}'y_{1}+x_{2}'y_{2}+\ldots x_{n}'y_{n}+\mathrm {S} '$

une des solutions de cette équation. Les coefficients $x_{1}',$ $x_{2}',$ $\ldots ,\,x_{n}'$ sont les constantes d’intégration que j’appelais jusqu’ici $x_{i}^{0},$ mais que j’appelle maintenant $x_{i}'$ parce que je vais bientôt les prendre pour variables indépendantes nouvelles.

Quant à $\mathrm {S} ',$ c’est une fonction périodique de

$m_{1}y_{1}+m_{2}y_{2}+\ldots +m_{n}y_{n}$

dépendant en outre de $x_{1}',$ $x_{2}',$ $\ldots ,\,x_{n}'\,;$ de sorte que la valeur moyenne de ${\frac {d\mathrm {S} }{dy_{i}}}$ n’est autre chose que $x_{i}'$ et que l’expression considérée de $\mathrm {S}$ ne diffère pas de celle à laquelle conduisent les équations (1) du n^o 202.

Posons maintenant

${\begin{aligned}x_{i}&={\frac {d\mathrm {S} }{dy_{i}}},&y_{i}'&=-{\frac {d\mathrm {S} }{dx_{i}'}}\cdot \end{aligned}}$

Prenons pour variables nouvelles les $x_{i}'$ et les $y_{i}'\,;$ la forme canonique des équations ne sera pas altérée ; la fonction $\mathrm {F}$ exprimée en fonctions des $x_{i}'$ et des $y_{i}'$ conservera la même forme ; seulement les coefficients des termes en

$m_{1}y_{1}'+m_{2}y_{2}'+\ldots +m_{n}y_{n}'$

seront beaucoup plus petits que ceux des termes correspondants en

$m_{1}y_{1}+m_{2}y_{2}+\ldots +m_{n}y_{n}.$

Les inégalités à longue période auront disparu parce qu’en somme on en aura tenu compte dès la première approximation.

Méthode de M. Bohlin.

204.L’inconvénient de la méthode de Delaunay, c’est d’exiger de nombreux changements de variables. Cet inconvénient peut être évité grâce à un procédé découvert par M. Bohlin et que j’ai proposé de mon côté, mais quelques jours après lui.

Reprenons nos équations générales

(1)

${\begin{aligned}{\frac {dx_{i}}{dt}}&={\frac {d\mathrm {F} }{dy_{i}}},&{\frac {dy_{i}}{dt}}&=-{\frac {d\mathrm {F} }{dx_{i}}}\end{aligned}}$

et supposons que l’expression

$m_{1}n_{1}^{0}+m_{2}n_{2}^{0}+\ldots +m_{n}n_{n}^{0}$

soit très petite.

Il s’agit d’intégrer l’équation

(2)

$\mathrm {F} \left({\frac {d\mathrm {S} }{dy_{1}}},\,{\frac {d\mathrm {S} }{dy_{2}}},\,\ldots ,\,{\frac {d\mathrm {S} }{dy_{n}}},\,y_{1},\,y_{2},\,\ldots ,\,y_{n}\right)=\mathrm {C} .$

Posons

${\begin{alignedat}{5}\mathrm {S} &=\mathrm {S} _{0}&{}+&{}\mathrm {S} _{1}{\sqrt {\mu }}&{}+&{}\mathrm {S} _{2}\,\mu &{}+&{}\mathrm {S} _{3}\mu {\sqrt {\mu }}+\ldots ,\\\mathrm {C} &=\mathrm {C} _{0}&{}+&{}\mathrm {C} _{2}\,\mu &{}+&{}\mathrm {C} _{4}\,\mu ^{2}&{}+&{}\ldots .\end{alignedat}}$

Substituons ces valeurs dans l’équation (2), ordonnons suivant les puissances de ${\sqrt {\mu }},$ et égalons les coefficients des puissances semblables de ${\sqrt {\mu }}\,;$ il viendra

(3)

$\left\{{\begin{aligned}\mathrm {F} _{0}\left({\frac {d\mathrm {S} _{0}}{dy_{1}}},{\frac {d\mathrm {S} _{0}}{dy_{2}}},\ldots ,{\frac {d\mathrm {S} _{0}}{dy_{n}}}\right)&=\mathrm {C} _{0},\\\sum {\frac {d\mathrm {F} _{0}}{dx_{i}}}{\frac {d\mathrm {S} _{1}}{dy_{i}}}&=0,\\\sum {\frac {d\mathrm {F} _{0}}{dx_{i}}}{\frac {d\mathrm {S} _{2}}{dy_{i}}}+{\tfrac {1}{2}}\sum {\frac {d^{2}\mathrm {F} _{0}}{dx_{i}\,dx_{k}}}{\frac {d\mathrm {S} _{1}}{dy_{i}}}{\frac {d\mathrm {S} _{1}}{dy_{k}}}&=\Phi +\mathrm {C} _{2},\\\sum {\frac {d\mathrm {F} _{0}}{dx_{i}}}{\frac {d\mathrm {S} _{3}}{dy_{i}}}+{\tfrac {1}{2}}\sum {\frac {d^{2}\mathrm {F} _{0}}{dx_{i}\,dx_{k}}}{\frac {d\mathrm {S} _{1}}{dy_{i}}}{\frac {d\mathrm {S} _{2}}{dy_{k}}}&=\Phi ,\\\sum {\frac {d\mathrm {F} _{0}}{dx_{i}}}{\frac {d\mathrm {S} _{4}}{dy_{i}}}+{\tfrac {1}{2}}\sum {\frac {d^{2}\mathrm {F} _{0}}{dx_{i}\,dx_{k}}}{\frac {d\mathrm {S} _{1}}{dy_{i}}}{\frac {d\mathrm {S} _{3}}{dy_{k}}}&=\Phi +\mathrm {C} _{4},\\.\ldots \ldots \ldots \ldots \ldots \ldots \ldots \ldots \ldots \ldots \ldots \ldots &\ldots \ldots \ldots .\end{aligned}}\right.$

Voici la signification de ces équations :

Je désigne encore par $\Phi$ toute fonction connue, et je suppose

Dans la troisième	équation (3) que $\mathrm {S} _{0}$ est connu,
Dans la quatrième	équation (3) que $\mathrm {S} _{0}$ et $\mathrm {S} _{1}$ sont connus,
Dans la cinquième	équation (3) que $\mathrm {S} _{0},$ $\mathrm {S} _{1}$ et $\mathrm {S} _{2}$ sont connus.

Le second membre contient tantôt $\Phi ,$ tantôt $\Phi +\mathrm {C} _{2p}$ parce que j’ai supposé que les constantes $\mathrm {C}$ d’indice impair, c’est-à-dire les coefficients des puissances impaires de ${\sqrt {\mu }}$ dans le développement de $\mathrm {C}$ sont nulles.

Il faut encore préciser le sens du signe ${\textstyle \sum }$ dans le second terme du premier membre des diverses équations (3). Ce signe porte sur les deux indices $i$ et $k\,;$ il faut convenir que dans la troisième équation (3), la combinaison $(i,k)$ apparaît deux fois si $i\gtrless k$ et une fois si $i=k,$ et que dans les autres équations (3) cette combinaison apparaît deux fois dans tous les cas.

Je suppose comme plus haut

${\frac {d\mathrm {S} _{0}}{dy_{i}}}=x_{i}^{0},$

les $x_{i}^{0}$ étant des constantes. Dans les dérivées de $\mathrm {F} _{0}$ qui figurent dans les équations (3), je suppose que les $x_{i}$ ont été remplacés par les $x_{i}^{0}$ de telle sorte que

${\frac {d\mathrm {F} _{0}}{dx_{i}}}=-n_{i}^{0}.$

Je suppose de plus que les $x_{i}^{0}$ aient été choisis de telle sorte que

(4)

${\textstyle \sum }\,m_{i}n_{i}^{0}=0,$

et qu’il n’y ait entre les $n_{i}^{0}$ aucune autre combinaison linéaire à coefficients entiers.

Proposons-nous de déterminer $\mathrm {S}$ de telle façon que les

${\frac {d\mathrm {S} _{p}}{dy_{i}}}$

soient des fonctions périodiques des $y_{i}.$

La première équation (3) détermine tout simplement $\mathrm {C} _{0}\,;$ la seconde s’écrit

(5)

${\textstyle \sum }\,n_{i}^{0}\,{\frac {d\mathrm {S} _{1}}{dy_{i}}}=0,$

et elle ne peut être satisfaite que si les ${\frac {d\mathrm {S} _{1}}{dy_{i}}}$ sont fonctions seulement de $m_{1}y_{1}+m_{2}y_{2}+\ldots +m_{n}y_{n}.$ Car si $\mathrm {S} _{1}$ contenait, par exemple, un terme

$\mathrm {A} \cos(p_{1}y_{1}+\ldots +p_{n}y_{n}),$

le premier membre de (5) contiendrait un terme

$-\mathrm {A} (p_{1}n_{1}^{0}+\ldots +p_{n}n_{n}^{0})\sin(p_{1}y_{1}+\ldots +p_{n}y_{n}),$

qui ne pourrait disparaître que si l’on avait

${\frac {p_{1}}{m_{1}}}={\frac {p_{2}}{m_{2}}}=\ldots ={\frac {p_{n}}{m_{n}}}\cdot$

On aura donc

$\mathrm {S} _{1}=\alpha _{1}y_{1}+\alpha _{2}y_{2}+\ldots +\alpha _{n}y_{n}+f(m_{1}y_{1}+m_{2}y_{2}+\ldots +m_{n}y_{n}),$

la dérivée de $f$ étant périodique.

Passons à la troisième équation (3), et égalons dans les deux membres de cette équation les termes qui dépendent des sinus et des cosinus des multiples de

$m_{1}y_{1}+m_{2}y_{2}+\ldots +m_{n}y_{n}.$

Le premier terme du premier membre, qui peut s’écrire

$-{\textstyle \sum }\,n_{i}^{0}\,{\frac {d\mathrm {S} _{2}}{dy_{i}}},$

ne contiendra pas de pareils termes ; car si $\mathrm {S} _{2}$ contenait un terme

$\mathrm {A} \cos(p_{1}y_{1}+\ldots +p_{n}y_{n}),$

où

${\frac {p_{1}}{m_{1}}}={\frac {p_{2}}{m_{2}}}=\ldots ={\frac {p_{n}}{m_{n}}},$

le terme correspondant de l’expression

$-{\textstyle \sum }\,n_{i}^{0}\,{\frac {d\mathrm {S} _{2}}{dy_{i}}}$

s’écrirait

${\textstyle \sum }\,\mathrm {A} (p_{1}n_{1}^{0}+\ldots +p_{n}n_{n}^{0})\sin(p_{1}y_{1}+\ldots +p_{n}y_{n})$

et s’annulerait en vertu de la relation (5).

Le second terme du premier membre ne dépend, au contraire, que de $\mathrm {S} _{1}$ et est fonction seulement de $m_{1}y_{1}+m_{2}y_{2}+\ldots +m_{n}y_{n}.$ Tous ces termes ne contiennent donc que des sinus ou des cosinus des multiples de

$m_{1}y_{1}+m_{2}y_{2}+\ldots +m_{n}y_{n}.$

Introduisons une notation nouvelle :

Soit $\mathrm {U}$ une fonction quelconque dont les dérivées ${\frac {d\mathrm {U} }{dy_{i}}}$ soient des fonctions périodiques de $\mathrm {U} \,;$ on pourra la développer en une série dont tous les termes seront d’une des formes suivantes

${\begin{array}{ll}\alpha _{i}y_{i},&\alpha \cos(p_{1}y_{1}+\ldots +p_{n}y_{n}),\\&\alpha \,\sin(p_{1}y_{1}+\ldots +p_{n}y_{n}).\end{array}}$

Supprimons dans cette série tous les termes trigonométriques, sauf ceux pour lesquels

${\frac {p_{1}}{m_{1}}}={\frac {p_{2}}{m_{2}}}=\ldots ={\frac {p_{n}}{m_{n}}}\cdot$

L’ensemble des termes restant pourra être désigné par ${\big [}\mathrm {U} {\big ]}$ et s’appeler la valeur moyenne de $\mathrm {U} .$

On aura alors

${\begin{aligned}\left[{\frac {d\mathrm {U} }{dy_{i}}}\right]&={\frac {d\left[\mathrm {U} \right]}{dy_{i}}}\,;&{\textstyle \sum }\,n_{i}^{0}\,{\frac {d\left[\mathrm {U} \right]}{dy_{i}}}&=\mathrm {const.} \end{aligned}}$

et, si $\mathrm {V}$ est une fonction périodique quelconque,

$\left[\left[\mathrm {V} \right]{\frac {d\mathrm {U} }{dy_{i}}}\right]=\left[\mathrm {V} \right]\left[{\frac {d\mathrm {U} }{dy_{i}}}\right]\cdot$

Il vient donc

(6)

$\left\{{\begin{aligned}-\left[{\textstyle \sum }\,n_{i}^{0}\,{\frac {d\mathrm {S} _{2}}{dy_{i}}}\right]&=\mathrm {const.} ,\\[0.5ex]\left[{\frac {d\mathrm {S} _{1}}{dy_{i}}}\,{\frac {d\mathrm {S} _{1}}{dy_{k}}}\right]&={\frac {d\mathrm {S} _{1}}{dy_{i}}}{\frac {d\mathrm {S} _{1}}{dy_{k}}},\\[0.5ex]{\big [}\Phi {\big ]}&=-{\big [}\mathrm {F} _{1}{\big ]}.\end{aligned}}\right.$

Dans $\mathrm {F} _{1},$ je suppose que les $x_{i}$ ont été remplacés par les $x_{i}^{0}\,;$ la fonction $\Phi$ qui entre dans la troisième équation (6) est celle de la troisième équation (3).

La constante du second membre de la première équation (6) peut être désignée par $\mathrm {C} _{2}-\mathrm {C} _{2}'.$

On trouvera alors, en égalant les valeurs moyennes des deux membres de la troisième équation (3)

(7)

${\tfrac {1}{2}}\sum {\frac {d^{2}\mathrm {F} _{0}}{dx_{i}\,dx_{k}}}{\frac {d\mathrm {S} _{1}}{dy_{i}}}{\frac {d\mathrm {S} _{1}}{dy_{k}}}=\mathrm {C} _{2}'-{\big [}\mathrm {F} _{1}{\big ]}.$

Cette équation est de même forme que celles que nous avons étudiées aux n^os 199 à 202, et en particulier de même forme que la seconde équation (4) du n^o 200.

Nous retrouverons donc, comme pour cette seconde équation (4), trois cas différents.

Rappelons-nous que $\mathrm {S} _{1}$ est de la forme

$\mathrm {S} _{1}=\alpha _{1}y_{1}+\alpha _{2}y_{2}+\ldots +\alpha _{n}y_{n}+f(m_{1}y_{1}+m_{2}y_{2}+\ldots +m_{n}y_{n}),$

d’où

${\frac {d\mathrm {S} _{1}}{dy_{i}}}=\alpha _{i}+m_{i}f'.$

Substituons cette valeur de ${\frac {d\mathrm {S} _{1}}{dy_{i}}}$ dans (7) ; cette équation deviendra une équation du second degré par rapport à $f'$ et nous pourrons l’écrire

(8)

$\mathrm {A} f'^{2}+2\mathrm {B} f'+\mathrm {D} =\mathrm {C} _{2}'-{\big [}\mathrm {F} _{1}{\big ]},$

où $\mathrm {A,\,B}$ et $\mathrm {D}$ sont des constantes dépendant des constantes $\alpha _{i}\,;$ ces dernières constantes $\alpha$ peuvent d’ailleurs être choisies arbitrairement.

Pour que $f',$ et par conséquent ${\frac {d\mathrm {S} _{1}}{dy_{i}}},$ soit une fonction périodique de $m_{1}y_{1}+m_{2}y_{2}+\ldots +m_{n}y_{n},$ il faut et il suffit que l’équation (8) ait toujours ses racines réelles, c’est-à-dire que l’inégalité

$\mathrm {B} ^{2}-\mathrm {AD} +\mathrm {AC} _{2}'-\mathrm {A} {\big [}\mathrm {F} _{1}{\big ]}>0,$

soit satisfaite pour toutes les valeurs de

$m_{1}y_{1}+m_{2}y_{2}+\ldots +m_{n}y_{n}.$

Comme les constantes $\alpha _{i}$ sont arbitraires, nous prendrons

(9)

$\alpha _{1}=\alpha _{2}=\ldots =\alpha _{n}=0.$

Nous ne restreignons pas ainsi la généralité, comme nous le verrons bientôt.

Cela reviendrait d’ailleurs au même de supposer

${\frac {\alpha _{1}}{m_{1}}}={\frac {\alpha _{2}}{m_{2}}}=\ldots ={\frac {\alpha _{n}}{m_{n}}},$

puisque, si cette condition est remplie, l expression

$\alpha _{1}y_{1}+\alpha _{2}y_{2}+\ldots +\alpha _{n}y_{n}$

devient une fonction de $m_{1}y_{1}+\ldots +m_{n}y_{n}$ seulement, que l’on peut faire rentrer dans $f.$

Quoi qu’il en soit, si l’on suppose les conditions (9) remplies, l’équation (8) se simplifie et s’écrit

(8 bis)

$\mathrm {A} f'^{2}=\mathrm {C} _{2}'-{\big [}\mathrm {F} _{1}{\big ]}.$

Supposons alors que l’on construise pour diverses valeurs de la constante $\mathrm {C} _{2}'$ des courbes en prenant pour rayon vecteur $f'+$ une constante quelconque et pour angle polaire

$m_{1}y_{1}+m_{2}y_{2}+\ldots +m_{n}y_{n},$

on obtiendra une figure tout à fait pareille à la fig. 3.

Supposons pour fixer les idées que $\mathrm {A}$ soit positif. Alors, pour que $f'$ soit périodique, il faut qu’il reste toujours réel, c’est-à-dire que $\mathrm {C} _{2}'$ soit plus grand que le maximum de ${\big [}\mathrm {F} _{1}{\big ]}.$

Dans ce cas $f',$ et par conséquent ${\frac {d\mathrm {S} _{1}}{dy_{i}}},$ est une fonction périodique de $m_{1}y_{1}+m_{2}y_{2}+\ldots +m_{n}y_{n}$ qui ne s’annule jamais.

Ayant ainsi déterminé $\mathrm {S} _{1},$ il s’agit maintenant de déterminer $\mathrm {S} _{2}\,;$ cette fonction doit être de la forme

$\alpha _{1}^{2}y_{1}+\alpha _{2}^{2}y_{2}+\ldots +\alpha _{n}^{2}y_{n}+\varphi ,$

$\varphi$ étant périodique, et en général $\mathrm {S} _{p}$ doit être de la forme

$\alpha _{1}^{p}y_{1}+\alpha _{2}^{p}y_{p}+\ldots +\alpha _{n}^{p}y_{n}+\varphi ,$

$\varphi$ étant périodique ; je supposerai pour simplifier

(10)

${\frac {\alpha _{1}^{p}}{m_{1}}}={\frac {\alpha _{2}^{p}}{m_{2}}}=\ldots ={\frac {\alpha _{n}^{p}}{m_{n}}},$

ce qui n’est pas, comme nous le verrons bientôt, restreindre la généralité.

Nous avons

$-\left[{\textstyle \sum }\,n_{i}^{0}\,{\frac {d\mathrm {S} _{p}}{dy_{i}}}\right]=\mathrm {C} _{p}'-\mathrm {C} _{p},$

équation analogue à la première des équations (6). Si les conditions (10) sont remplies, on aura $\mathrm {C} _{p}'=\mathrm {C} _{p}$ et en particulier $\mathrm {C} _{2}'=\mathrm {C} _{2}.$

Cela posé, revenons à la troisième équation (3) qui peut s’écrire, maintenant que nous nous sommes donné $\mathrm {C} _{2}$ et que $\mathrm {S} _{1}$ est entièrement déterminée,

(11)

${\textstyle \sum }\,n_{i}^{0}\,{\frac {d\mathrm {S} _{2}}{dy_{i}}}=\Phi .$

La fonction connue $\Phi$ est périodique en $y_{1},$ $y_{2},$ $\ldots ,\,y_{n}.$

Soit donc

$\Phi ={\textstyle \sum }\,\mathrm {A} \cos(p_{1}y_{1}+p_{2}y_{2}+\ldots +p_{n}y_{n}+\beta ),$

l’équation (11) donnera

${\begin{aligned}\mathrm {S} _{2}=&{\textstyle \sum }\,{\frac {\mathrm {A} \sin(p_{1}y_{1}+p_{2}y_{2}+\ldots +p_{n}y_{n}+\beta )}{p_{1}n_{1}^{0}+p_{2}n_{2}^{0}+\ldots +p_{n}n_{n}^{0}}}\\&+\psi (m_{1}y_{1}+m_{2}y_{2}+\ldots +m_{n}y_{n}),\end{aligned}}$

$\psi$ étant une fonction arbitraire de $m_{1}y_{1}+m_{2}y_{2}+\ldots +m_{n}y_{n}.$ Cette solution deviendrait illusoire si, pour un terme quelconque de $\Phi ,$ on avait

$p_{1}n_{1}^{0}+p_{2}n_{2}^{0}+\ldots +p_{n}n_{n}^{0}=0,$

c’est-à-dire

${\frac {p_{1}}{m_{1}}}={\frac {p_{2}}{m_{2}}}=\ldots ={\frac {p_{n}}{m_{n}}}\cdot$

Mais cela ne peut arriver parce que

${\big [}\Phi {\big ]}=0.$

En effet, nous venons précisément de déterminer $\mathrm {S} _{1}$ de telle façon que les valeurs moyennes des deux membres de la troisième équation (3) soient égales. Il doit donc en être de même des deux membres de l’équation (11), qui ne diffère de la troisième équation (3) que parce que certains termes ont passé d 'un membre dans l’autre.

Or

$\left[{\textstyle \sum }\,n_{i}^{0}\,{\frac {d\mathrm {S} _{2}}{dy_{i}}}\right]=0,$

puisque

$\mathrm {C} _{2}'=\mathrm {C} _{2}.$

Donc

${\big [}\Phi {\big ]}=0.$

C.Q.F.D.

Pour achever de connaître $\mathrm {S} _{2},$ il reste à déterminer la fonction arbitraire

$\psi ={\big [}\mathrm {S} _{2}{\big ]}.$

À cet effet, égalons les valeurs moyennes des deux membres de la quatrième équation (3). Il vient, en vertu des relations (10),

$\left[{\textstyle \sum }\,n_{i}^{0}\,{\frac {d\mathrm {S} _{3}}{dy_{i}}}\right]=0,$

et de plus

$\left[{\frac {d^{2}\mathrm {F} _{0}}{dx_{i}\,dx_{k}}}{\frac {d\mathrm {S} _{1}}{dy_{i}}}{\frac {d\mathrm {S} _{2}}{dy_{k}}}\right]={\frac {d^{2}\mathrm {F} _{0}}{dx_{i}\,dx_{k}}}{\frac {d\mathrm {S} _{1}}{dy_{i}}}{\frac {d[\mathrm {S} _{2}]}{dy_{k}}},$

puisque $\mathrm {S} _{1}$ ne dépend que de $m_{1}y_{1}+m_{2}y_{2}+\ldots +m_{n}y_{n}.$ Nous obtenons donc

${\tfrac {1}{2}}\sum {\frac {d^{2}\mathrm {F} _{0}}{dx_{i}\,dx_{k}}}{\frac {d\mathrm {S} _{1}}{dy_{i}}}{\frac {d[\mathrm {S} _{2}]}{dy_{k}}}={\big [}\Phi {\big ]}.$

Si nous désignons par ${\big [}\mathrm {S} _{2}'{\big ]}$ la dérivée de ${\big [}\mathrm {S} _{2}{\big ]}$ par rapport à

$m_{1}y_{1}+m_{2}y_{2}+\ldots +m_{n}y_{n},$

il viendra

${\begin{aligned}{\frac {d\mathrm {S} _{1}}{dy_{i}}}&=m_{i}f',{\frac {d[\mathrm {S} _{2}]}{dy_{k}}}&=m_{k}{\big [}\mathrm {S} _{2}'{\big ]},\end{aligned}}$

et nous pourrons écrire

${\tfrac {1}{2}}\sum {\frac {d^{2}\mathrm {F} _{0}}{dx_{i}\,dx_{k}}}m_{i}m_{k}{\big [}\mathrm {S} _{2}'{\big ]}={\frac {{\big [}\Phi {\big ]}}{f'}}\cdot$

Comme $f'$ ne s’annule pas, ${\big [}\mathrm {S} _{2}'{\big ]}$ est une fonction périodique de $m_{1}y_{1}+\ldots +m_{n}y_{n},$ qui ne devient pas infinie et ${\big [}\mathrm {S} _{2}{\big ]}$ est de la forme

$a(m_{1}y_{1}+\ldots +m_{n}y_{n})+\psi ,$

$a$ étant un coefficient constant et $\psi$ une série ordonnée suivant les sinus et cosinus des multiples de $m_{1}y_{1}+m_{2}y_{2}+\ldots +m_{n}y_{n}.$

$\mathrm {S} _{2}$ étant ainsi entièrement déterminé, la quatrième équation (3) s’écrit

${\textstyle \sum }\,n_{i}^{0}\,{\frac {d\mathrm {S} _{3}}{dy_{i}}}=\Phi ,$

elle prend une forme tout à fait analogue à celle de l’équation (11), et se traite de la même manière. Et ainsi de suite.

J’ai dit plus haut que les hypothèses (9) et (10) ne restreignaient pas la généralité.

Et en effet considérons une solution de notre équation fondamentale et conforme à ces hypothèses (9) et (10) ; soit $\mathrm {S}$ cette solution et soit

$\mathrm {S} =\mathrm {S} _{0}+{\sqrt {\mu }}\,\mathrm {S} _{1}+\mu \,\mathrm {S} _{2}+\ldots .$

Soit, d’autre part,

$\mathrm {S} _{0}=x_{1}^{0}y_{1}+x_{2}^{0}y_{2}+\ldots +x_{n}^{0}y_{n},$

et

$\mathrm {S} _{p}=\alpha _{1}^{p}y_{1}+\alpha _{2}^{p}y_{2}+\ldots +\alpha _{n}^{p}y_{n}+{}$ fonction périodique.

Les $\alpha$ satisferont en vertu des hypothèses (9) et (10) à la condition

${\frac {\alpha _{1}^{p}}{m_{1}}}={\frac {\alpha _{2}^{p}}{m_{2}}}=\ldots ={\frac {\alpha _{n}^{p}}{m_{n}}}$

et seront d’ailleurs des fonctions des constantes d’intégration $x_{i}^{0}$ et $\mathrm {C} _{p}.$

Comme les $x_{i}^{0}$ sont des constantes arbitraires, je puis les remplacer par des développements quelconques

$x_{i}^{0}=\beta _{i}^{0}+{\sqrt {\mu }}\,\beta _{i}^{1}+\mu \,\beta _{i}^{2}+\ldots ,$

les $\beta _{i}^{p}$ étant de nouvelles constantes arbitraires.

Si dans $\mathrm {S}$ nous remplaçons les $x_{i}^{0}$ par ces développements, puis que nous ordonnions de nouveau par rapport aux puissances de ${\sqrt {\mu }},$ il viendra

$\mathrm {S} =\mathrm {S} _{0}'+{\sqrt {\mu }}\mathrm {S} _{1}'+\mu \,\mathrm {S} _{2}'+\ldots ,$

où

$\mathrm {S} _{p}'=\alpha _{1}'^{p}y_{1}+\alpha _{2}'^{p}y_{2}+\ldots \alpha _{n}'^{p}y_{n}+{}$ fonction périodique,

et nous aurons pu choisir les $\beta _{i}^{p}$ de telle façon que les constantes $\alpha _{i}'^{p}$ soient quelconques,

Nos hypothèses n’ont donc apporté à la généralité aucune restriction essentielle. C.Q.F.D.

Cas de la libration.

205.Qu’arrivera-t-il maintenant si $\mathrm {C} _{2}$ n’est pas plus grand que le maximum de ${\big [}\mathrm {F} _{1}{\big ]}$ et si par conséquent $\mathrm {S} _{1}$ n’est pas toujours réel ? Dans ces cas où l’on dit qu’il y a libration, certaines difficultés se présentent que l’on peut vaincre par un artifice analogue à l’emploi que nous avons fait des fonctions elliptiques dans le n^o 199. Pour simplifier un peu l’exposition je supposerai

$m_{1}=1,\qquad m_{2}=m_{3}=\ldots =m_{n}=0.$

J’en ai le droit, car, s’il n’en était pas ainsi, je pourrais faire un changement de variables analogue au changement de variables (3) du n^o 202.

Nous ne pouvons plus nous arranger de manière que les ${\frac {d\mathrm {S} _{p}}{dy_{i}}}$ soient des fonctions périodiques de $y_{1},$ $y_{2},$ $\ldots ,\,y_{n}\,;$ mais nous pouvons du moins chercher à trouver une fonction $\mathrm {S}$ telle que les ${\frac {d\mathrm {S} _{p}}{dy_{i}}}$ soient des fonctions périodiques de

$y_{2},\quad y_{3},\quad .,\quad y_{n}.$

Alors ce que nous avons appelé ${\big [}\mathrm {U} {\big ]}$ dans le numéro précédent n’est autre chose que la valeur moyenne de $\mathrm {U}$ considérée comme fonction périodique de $y_{2},$ $y_{3},$ $\ldots ,\,y_{n}.$

On a donc

(12)

$\left[{\textstyle \sum }\,n_{i}^{0}\,{\frac {d\mathrm {S} _{p}}{dy_{i}}}\right]=\mathrm {const.} ,$

et en effet

$\left[{\frac {d\mathrm {S} _{p}}{dy_{2}}}\right],\quad \left[{\frac {d\mathrm {S} _{p}}{dy_{3}}}\right],\quad \ldots ,\quad \left[{\frac {d\mathrm {S} _{p}}{dy_{n}}}\right],\quad$

se réduisent à des constantes et, d’autre part, la relation

${\textstyle \sum }\,m_{i}n_{i}^{0}=0$

se réduit ici à

$n_{1}^{0}=0,$

de sorte que le premier membre de (12) ne contient pas de terme en $\left[{\frac {d\mathrm {S} _{p}}{dy_{1}}}\right]\cdot$

Je pourrai supposer que non seulement les ${\frac {d\mathrm {S} _{p}}{dy_{i}}},$ mais encore les $\mathrm {S} _{p}$ (du moins pour $p>0$) sont des fonctions périodiques de $y_{1},$ $y_{2},$ $\ldots ,\,y_{n}\,;$ c’est là une hypothèse identique aux hypothèses (9) et (10) du numéro précédent qui, nous l’avons vu, ne restreignent pas la généralité. Si on l’admet, la constante du second membre de (12) est nulle.

Cela posé, reprenons les équations (3) du numéro précédent. La seconde nous apprend que $\mathrm {S} _{1}$ ne dépend que de $y_{1}$ et la troisième, quand on égale les valeurs moyennes des deux membres, donne

(13)

${\frac {1}{2}}\,{\frac {d^{2}\mathrm {F} _{0}}{dx_{1}^{2}}}\left({\frac {d\mathrm {S} _{1}}{dy_{1}}}\right)^{2}=\mathrm {C} _{2}-{\big [}\mathrm {F} _{1}{\big ]},$

ce qui détermine $\mathrm {S} _{1}.$

En tenant compte de l’équation (13) la troisième équation (3) devient

(14)

$-{\textstyle \sum }\,n_{i}^{0}\,{\frac {d\mathrm {S} _{2}}{dy_{i}}}={\big [}\mathrm {F} _{1}{\big ]}-\mathrm {F} _{1}.$

Comme le second membre est une fonction de $y_{1},$ $y_{3},$ $\ldots ,\,y_{n}$ dont la valeur moyenne est nulle, l’application d’un procédé d’intégration dont nous avons déjà fait usage bien des fois nous donnera $\mathrm {S} _{2}$ à une fonction arbitraire près de $y_{1},$ c’est-à-dire que l’équation (14) nous fera connaître

$\mathrm {S} _{2}-{\big [}\mathrm {S} _{2}{\big ]}.$

Pour déterminer ${\big [}\mathrm {S} _{2}{\big ]}$ prenons la quatrième équation (3) et égalons les valeurs moyennes des deux membres, il viendra

(15)

${\frac {d^{2}\mathrm {F} _{0}}{dx_{1}^{2}}}{\frac {d[\mathrm {S} _{2}]}{dy_{1}}}{\frac {d\mathrm {S} _{1}}{dy_{1}}}={\big [}\Phi {\big ]}.$

Nous tirerons de là la valeur de ${\big [}\mathrm {S} _{2}{\big ]}.$

Connaissant $\mathrm {S} _{2}$ et tenant compte de (15), nous pourrons écrire la quatrième équation (3) sous la forme

$-{\textstyle \sum }\,n_{i}^{0}\,{\frac {d\mathrm {S} _{3}}{dy_{i}}}=\Phi .$

La valeur moyenne de $\Phi$ étant nulle, cette équation, qui est de même forme que (14), se traitera de la même manière et nous donnera

$\mathrm {S} _{3}-{\big [}\mathrm {S} _{3}{\big ]}$

et ainsi de suite.

On voit que les fonctions ${\frac {d\mathrm {S} _{p}}{dy_{i}}}$ ainsi déterminées sont des fonctions uniformes de $y_{1}$ et de ${\sqrt {\mathrm {C} _{2}-{\big [}\mathrm {F} _{1}{\big ]}}}.$

206.Pour étudier plus complètement nos fonctions, il faut faire un changement de variables. Pour cela introduisons une fonction auxiliaire $\mathrm {T}$ définie de la façon suivante ; nous aurons

$\mathrm {T} =\mathrm {T} _{0}+\mathrm {T} _{1}{\sqrt {\mu }}+\mathrm {T} _{2}\,\mu$

et

$\mathrm {T} _{0}=x_{1}^{0}y_{1}+x_{2}^{0}y_{2}+\ldots +x_{n}^{0}y_{n},$

où les $x_{i}^{0}$ seront des constantes qui satisferont aux conditions

$\mathrm {F} _{0}=\mathrm {C} _{0},\qquad n_{i}^{0}=0.$

En d’autres termes, $\mathrm {T} _{0}$ ne sera pas autre chose que ce que nous avons appelé $\mathrm {S} _{0}.$

Pour définir $\mathrm {T} _{1}$ nous partirons de la même équation qui a servi à définir $\mathrm {S} _{1},$ c’est-à-dire de l’équation (7) du n^o 204, où nous remplacerons $\mathrm {S} _{1}$ par $\mathrm {T} _{1}$ et $\mathrm {C} _{2}'$ par $\mathrm {C} _{2},$ ce qui nous donne

(7 bis)

${\tfrac {1}{2}}\sum {\frac {d^{2}\mathrm {F} _{0}}{dx_{i}^{0}\,dx_{k}^{0}}}\,{\frac {d\mathrm {T} _{1}}{dy_{i}}}\,{\frac {d\mathrm {T} _{1}}{dy_{k}}}=\mathrm {C} _{2}-{\big [}\mathrm {F} _{1}{\big ]}.$

J’y adjoindrai les suivantes (où les $x_{i}'$ sont des constantes)

${\frac {d\mathrm {T} _{1}}{dy_{i}}}=x_{i}'\quad (i=2,\,3,\,\ldots ,\,n).$

Il importe de remarquer qu’en faisant cette dernière hypothèse je définirai $\mathrm {T} _{1}$ comme j’ai fait plus haut pour $\mathrm {S} _{1},$ mais en m’écartant des hypothèses (9) qui exigeraient que les constantes $x_{i}'$ fussent nulles.

Comme les coefficients ${\frac {d^{2}\mathrm {F} _{0}}{dx_{i}^{0}\,dx_{k}^{0}}}$ ne dépendent que des $x_{i}^{0},$ ce sont des constantes ; si donc je remplace les ${\frac {d\mathrm {T} _{1}}{dy_{i}}}$ par les $x_{i}',$ l’équation (7 bis) deviendra

(8 ter)

$\mathrm {A} \left({\frac {d\mathrm {T} _{1}}{dy_{1}}}\right)^{2}+2\mathrm {B} \,{\frac {d\mathrm {T} _{1}}{dy_{1}}}+\mathrm {D} =\mathrm {C} _{2}-{\big [}\mathrm {F} _{1}{\big ]},$

où $\mathrm {A}$ est une constante, $\mathrm {B}$ et $\mathrm {D}$ deux polynômes homogènes par rapport aux $x_{i}',$ le premier du premier degré, le second du second degré. Nous tirerons de là

${\frac {d\mathrm {T} _{1}}{dy_{1}}}=-{\frac {\mathrm {B} }{\mathrm {A} }}\pm {\sqrt {{\frac {\mathrm {B} ^{2}}{\mathrm {A} ^{2}}}-{\frac {\mathrm {D} }{\mathrm {A} }}+{\frac {\mathrm {C} _{2}}{\mathrm {A} }}-{\frac {[\mathrm {F} _{1}]}{\mathrm {A} }}}}\cdot$

Je poserai

${\frac {\mathrm {B} ^{2}}{\mathrm {A} ^{2}}}-{\frac {\mathrm {D} }{\mathrm {A} }}+{\frac {\mathrm {C} _{2}}{\mathrm {A} }}=x_{1}',$

et pour abréger l’écriture

${\big [}\mathrm {F} _{1}{\big ]}=\mathrm {A} \,\psi ,$

d’où

$\mathrm {T} _{1}=x_{2}'y_{2}+x_{3}'y_{3}+\ldots +x_{n}'y_{n}-{\frac {\mathrm {B} y_{1}}{\mathrm {A} }}+\int dy_{1}\,{\sqrt {x_{1}'-\psi }}.$

Nous déterminerons ensuite $\mathrm {T} _{2}$ par l’équation

${\textstyle \sum }\,n_{i}^{0}\,{\frac {d\mathrm {T} _{2}}{dy_{i}}}=\mathrm {F} _{1}-{\big [}\mathrm {F} _{1}{\big ]},$

analogue à l’équation (11) du n^o 204.

Cette équation détermine $\mathrm {T} _{2},$ comme nous l’avons vu, à une fonction arbitraire près de $y_{1}\,;$ nous pourrions, sans inconvénient, faire un choix quelconque ; nous supposerons par exemple

${\big [}\mathrm {T} _{2}{\big ]}=0.$

Je poserai

${\textstyle \sum }\,n_{i}^{0}x_{i}'=-\mathrm {C} _{1}.$

Il résulte de là :

1^o Que $\mathrm {T} _{2}$ est une fonction périodique des $y_{i}$ qui ne dépend pas des $x_{i}'\,;$ car il en est ainsi de $\mathrm {F} _{1}$ et de ${\big [}\mathrm {F} _{1}{\big ]}$ où nous avons supposé tout simplement que les $x_{i}$ étaient remplacés par les constantes $x_{i}^{0}.$

2^o Que si dans le premier membre de l’équation (2) du n^o 204 on remplace $\mathrm {S}$ par $\mathrm {T} ,$ ce premier membre se réduit à

$\mathrm {C} _{0}+\mathrm {C} _{1}{\sqrt {\mu }}+\mathrm {C} _{2}\,\mu ,$

à des termes près contenant $\mu {\sqrt {\mu }}$ en facteur ; car les fonctions $\mathrm {T} _{0},$ $T_{1}$ et $T_{2}$ satisfont aux trois premières équations (3), sauf que dans la seconde de ces équations le zéro du second membre doit être remplacé par $\mathrm {C} _{1}.$

Posons maintenant

(16)

$\left\{{\begin{aligned}x_{1}&={\frac {d\mathrm {T} }{dy_{1}}}=x_{1}^{0}+{\sqrt {\mu }}\left(-{\frac {\mathrm {B} }{\mathrm {A} }}+{\sqrt {x_{1}'-\psi }}\right)+\mu \,{\frac {d\mathrm {T} _{2}}{dy_{1}}},\\y_{1}'&={\frac {d\mathrm {T} }{dx_{1}'}}={\frac {\sqrt {\mu }}{2}}\int {\frac {dy_{1}}{\sqrt {x_{1}'-\psi }}},\\x_{i}&={\frac {d\mathrm {T} }{dy_{i}}}=x_{i}^{0}+x_{i}'{\sqrt {\mu }}+\mu \,{\frac {d\mathrm {T} _{2}}{dy_{i}}},\\y_{i}'&={\frac {d\mathrm {T} }{dx_{i}'}}=y_{i}{\sqrt {\mu }}-{\frac {y_{1}{\sqrt {\mu }}}{\mathrm {A} }}{\frac {d\mathrm {B} }{dx_{i}'}}\quad (i=2,\,3,\,.,\,n).\end{aligned}}\right.$

Si l’on prend comme variables nouvelles les $x_{i}'$ et les $y_{i}'$ à la place des $x_{i}$ et des $y_{i},$ la forme canonique des équations ne sera pas altérée.

Étudions d’abord la troisième équation (16) où entrent $y_{1}',$ $y_{1}$ et $x_{1}'\,;$ si nous considérons $x_{1}'$ comme une constante et si nous faisons varier seulement $y_{1}',$ je dis que $y_{1}$ est une fonction périodique de $y_{1}'.$

C’est ici qu’éclate l’analogie avec l’emploi des fonctions elliptiques au n^o 199. Dans le cas particulier traité dans ce numéro, on avait

${\begin{aligned}\mathrm {A} &=1,&{\big [}\mathrm {F} _{1}{\big ]}&=\cos y_{1},\end{aligned}}$

de sorte que notre troisième équation (16) s’écrivait

$y_{1}'={\frac {\sqrt {\mu }}{2}}\int {\frac {dy_{1}}{\sqrt {\mathrm {C} _{2}-\cos y_{1}}}}\cdot$

L’intégrale du second membre est une intégrale elliptique et par conséquent $\cos y_{1}$ et $\sin y_{1}$ sont des fonctions doublement périodiques de $y_{1}'.$ Mais deux cas sont à distinguer suivant que

$\mathrm {C} _{2}>1$ou$\mathrm {C} _{2}<1.$

Si $\mathrm {C} _{2}>1$ la période réelle est égale à

${\frac {\sqrt {\mu }}{2}}\int _{0}^{2\pi }{\frac {dy_{1}}{\sqrt {\mathrm {C} _{2}-\cos y_{1}}}},$

et si

$\mathrm {C} _{2}=\cos \alpha <1$

la période réelle est égale à

${\sqrt {\mu }}\int _{-\alpha }^{+\alpha }{\frac {dy_{1}}{\sqrt {\mathrm {C} _{2}-\cos y_{1}}}}\cdot$

Dans ce cas particulier d’ailleurs, $y_{1}$ est une fonction uniforme de $y_{1}'$ pour les valeurs imaginaires aussi bien que pour les valeurs réelles de $y_{1}'.$ Mais, dans le cas général, $y_{1}$ est fonction uniforme de $y_{1}'$ pour les valeurs réelles seulement et, d’autre part, $\cos y_{1}$ et $\sin y_{1}$ admettent une période réelle qui est

${\frac {\sqrt {\mu }}{2}}\int _{0}^{2\pi }{\frac {dy_{1}}{\sqrt {x_{1}'-\psi }}}$

si $x_{1}'$ est supérieur au maximum de ${\big [}\psi {\big ]}$ ;

${\sqrt {\mu }}\int _{\alpha }^{\beta }{\frac {dy_{1}}{\sqrt {x_{1}'-\psi }}}$

si $x_{1}'$ est inférieur à ce maximum et si $x_{1}'-\psi$ s’annule pour $y_{1}=\alpha$ et pour $y_{1}=\beta$ et reste positif pour $\alpha <y_{1}<\beta .$ J’ajouterai que dans le premier cas $y_{1}$ augmente de $2\pi$ quand $y_{1}'$ augmente d’une période, tandis que dans le second cas, c’est-à-dire dans le cas de la libration, $y_{1}$ reprend sa valeur primitive quand $y_{1}'$ augmente d’une période.

Dans le cas particulier du n^o 199, non seulement $\cos y_{1}$ et $\sin y_{1}$ sont fonctions doublement périodiques de $y_{1}',$ mais il en est de même de ${\sqrt {\mathrm {C} _{2}-\cos y_{1}}}\,;$ quant à

$\mathrm {S} _{1}=\int {\sqrt {\mathrm {C} _{2}-\cos y_{1}}}\,dy_{1},$

il augmente d’une quantité constante quand $y_{1}'$ augmente d’une période.

De même, dans le cas général,

${\sqrt {x_{1}'-\psi }}\quad {\bigg (}$et par conséquent ${\frac {d\mathrm {T} _{1}}{dy_{1}}}{\bigg )}$

est une fonction périodique de $y_{1}'.$ Cette fonction, de même que $y_{1},$ dépend en outre de $x_{1}'$ qui joue un rôle analogue à celui du module dans le cas des fonctions elliptiques.

Observons avant d’aller plus loin que la période de ces diverses fonctions périodiques de $y_{1}$ est proportionnelle à ${\sqrt {\mu }}.$

Il résulte de là que, dans le cas de la libration, $x_{1},$ $x_{i},$ $y_{1}$ et $y_{i}'-y_{i}{\sqrt {\mu }}$ sont des fonctions périodiques de $y_{1}'\,;$ en outre $x_{1}$ et $x_{i}$ dépendent des $y_{i},$ mais ce sont des fonctions périodiques de période $2\pi$ de ces $n-1$ variables.

Si donc nous exprimons les variables anciennes $x_{i}$ et $y_{i}$ en fonctions des nouvelles $x_{i}'$ et $y_{i}',$ il est évident que les $x_{i},$ les $\cos y_{i}$ et les $\sin y_{i}$ sont des fonctions périodiques des $y_{i}'\,;$ il en est donc de même de $\mathrm {F}$ qui est périodique de période $2\pi$ par rapport aux $y_{i}.$

La période sera égale à

${\sqrt {\mu }}\int _{\alpha }^{\beta }{\frac {dy_{1}}{\sqrt {x_{1}'-\psi }}}$

pour $y_{1}'$ et à $2\pi {\sqrt {\mu }}$ pour les $y_{i}'\,;$ je poserai pour abréger la période relative à $y_{1}'$ égale à $\mathrm {P} {\sqrt {\mu }}\,;$ il est clair que $\mathrm {P}$ est une fonction de $x_{1}',$ de même que la période des fonctions elliptiques est une fonction du module.

Si nous posons

$y_{i}'=z_{i}{\sqrt {\mu }},$

d’où

(16 bis)

${\begin{aligned}z_{1}&={\frac {1}{2}}\int {\frac {dy_{1}}{\sqrt {x_{1}'-\psi }}},&z_{i}&=y_{i}-{\frac {y_{1}}{\mathrm {A} }}{\frac {d\mathrm {B} }{dx_{i}'}},\end{aligned}}$

$\mathrm {F}$ sera une fonction périodique des $z_{i}\,;$ la période sera $\mathrm {P}$ pour $z_{1}$ et $2\pi$ pour les autres $z_{i}\,;$ $\mathrm {F}$ sera en o’utre fonction des $x_{i}'\,;$ cette fonction sera développable suivant les puissances de ${\sqrt {\mu }}\,;$ les trois premiers termes du développement

$\mathrm {C} _{0}+\mathrm {C} _{1}{\sqrt {\mu }}+\mathrm {C} _{2}\,\mu$

seront indépendants des $z_{i}$ et fonctions seulement des $x_{i}'.$ Le premier terme $\mathrm {C} _{0}$ est une constante absolue ; $\mathrm {C} _{1}$ est, par définition, une fonction linéaire des $x_{i}'$ indépendante de $x_{1}'\,;$ enfin on a

$\mathrm {C} _{2}=\mathrm {A} \,x_{1}'+\mathrm {D} -{\frac {\mathrm {B} ^{2}}{\mathrm {A} }},$

d’où il résulte que $\mathrm {C} _{2}$ est un polynôme de premier ordre par rapport aux autres $x_{i}'.$

Posons maintenant

$\mathrm {F} =\mathrm {C} _{0}+\mathrm {F} ^{\star }{\sqrt {\mu }},$

nos équations deviendront

(17)

${\begin{aligned}{\frac {dx_{i}'}{dt}}&={\frac {d\mathrm {F} ^{\star }}{dz_{i}}},&{\frac {dz_{i}}{dt}}&=-{\frac {d\mathrm {F} ^{\star }}{dx_{i}'}}\cdot \end{aligned}}$

La fonction $\mathrm {F} ^{\star }$ est, comme la fonction $\mathrm {F} ,$ au n^o 125, périodique par rapport aux variables de la seconde série qui sont ici les $z_{i}.$

Toutefois deux obstacles empêchent que les procédés du n^o 125 soient immédiatement applicables aux équations (17).

1^o La fonction $\mathrm {F} ^{\star }$ est bien périodique par rapport aux $z_{i},$ mais, par rapport à $z_{1},$ la période n’est pas $2\pi ,$ mais $\mathrm {P} .$

Pour tourner cette première difficulté, il suffit d’un simple changement de variables. Si nous faisons

(18)

${\begin{aligned}u_{1}&=\int {\frac {\mathrm {P} \,dx_{1}'}{2\pi }},&v_{1}&={\frac {2\pi z_{1}}{\mathrm {P} }}\end{aligned}}$

les équations restent canoniques et s’écrivent

(19)

$\;\left\{{\begin{aligned}{\frac {du_{1}}{dt}}&={\frac {d\mathrm {F} ^{\star }}{dv_{1}}},&{\frac {dv_{1}}{dt}}&=-{\frac {d\mathrm {F} ^{\star }}{du_{1}}},\\{\frac {dx_{i}'}{dt}}&={\frac {d\mathrm {F} ^{\star }}{dz_{i}}},&{\frac {dz_{1}}{dt}}&=-{\frac {d\mathrm {F} ^{\star }}{dx_{1}'}}\qquad (i=2,\,3,\,\ldots ,\,n),\end{aligned}}\right.$

et cette fois $\mathrm {F} ^{\star }$ est périodique de période $2\pi$ par rapport à

$v_{1},\quad z_{2},\quad z_{3},\quad \ldots ,\quad z_{n}.$

2^o Si l’on fait $\mu =0,$ $\mathrm {F} ^{\star }$ se réduit à $\mathrm {C} _{1},$ et $\mathrm {C} _{1}$ ne dépend pas de toutes les variables de la première série, mais seulement de

$x_{2}',\quad x_{3}',\quad \ldots ,\quad x_{n}',$

car $n_{i}^{0}$ est nul. Nous ne sommes donc pas dans les conditions du n^o 125, mais dans celles du n^o 134 ; nous allons voir que les conclusions de ce numéro sont applicables.

En effet, la fonction qui correspond à celle que nous avons appelée $\mathrm {R}$ dans ce n^o 134, c’est ici $\mathrm {C} _{2}\,;$ et il est aisé de voir que $\mathrm {C} _{2}$ dépend de $x_{1}'$ et par conséquent de $u_{1}$ et ne dépend que des variables de la première série.

Les conditions pour que le théorème du n^o 134 soit vrai sont donc remplies et nous devons conclure qu’il existe $n$ fonctions

$u_{1},\quad x_{2}',\quad x_{3}',\quad \ldots ,\quad x_{n}'$

qui dépendent de $n$ variables

$u_{1},\quad z_{2},\quad z_{3},\quad \ldots ,\quad z_{n}$

et de $n$ constantes arbitraires et qui satisfont aux conditions suivantes :

1^o Quand on les substitue dans $\mathrm {F} ^{\star },$ cette fonction se réduit à une constante.

2^o L’expression

$u_{1}\,dv_{1}+x_{2}'\,dz_{2}+x_{3}'\,dz_{3}+\ldots +x_{n}'\,dz_{n}=d\mathrm {V}$

est une différentielle exacte.

3^o Ces $n$ fonctions sont périodiques de période $2\pi$ par rapport à

$v_{1},\quad z_{2},\quad z_{3},\quad \ldots ,\quad z_{n}.$

Considérons donc $u_{1}$ et les $x_{i}'$ comme fonctions de $v_{1}$ et des $z_{i},$ ce qui nous donne $n$ relations entre ces $2n$ variables, puis revenons aux variables anciennes $x_{i}$ et $y_{i}$ à l’aide des équations (16), (16 bis) et (18) ; nous obtiendrons ainsi $n$ relations entre les $x_{i}$ et les $y_{i}\,;$ en résolvant ces relations par rapport aux $x_{i},$ nous aurons les $x_{i}$ en fonctions des $y_{i},$ et il est clair que :

1^o Si l’on substitue dans $\mathrm {F}$ à la place des $x_{i}$ leurs valeurs en fonctions des $y_{i},$ $\mathrm {F}$ se réduit à une constante.

2^o L’expression

(20)

${\textstyle \sum }\,x_{i}\,dy_{i}=d\mathrm {S}$

est une différentielle exacte.

Car, d’après la forme des équations (16), (16 bis) et (18), la différence

$d\mathrm {S} -{\sqrt {\mu }}\,d\mathrm {V}$

est toujours une différentielle exacte.

3^o Si l’on exprime les $x_{i}$ en fonctions de $v_{1}$ et des $z_{i},$ les $x_{i}$ sont des fonctions périodiques de ces variables ; et, de même, si l’on exprime les $x_{i}$ en fonctions des $y_{i},$ ces fonctions seront périodiques de période $2\pi$ par rapport à $y_{2},$ $y_{3},$ $\ldots ,\,y_{n}.$

Il résulte de là que les fonctions $\mathrm {S}$ définies par l’équation (20) ne diffèrent pas de celles dont nous nous sommes occupés au numéro précédent, puisque nous n’avons fait intervenir dans leur définition que l’équation (2) du n^o 204 et la condition que les ${\frac {d\mathrm {S} }{dy_{i}}}$ soient périodiques par rapport à $y_{2},$ $y_{3},$ $\ldots ,\,y_{n}.$

Ainsi les deux systèmes d’équations

(21)

$\;\left\{{\begin{aligned}u_{1}&={\frac {d\mathrm {V} }{dv_{1}}},&x_{1}'&={\frac {d\mathrm {V} }{dz_{i}}},\qquad u_{1}=\int {\frac {\mathrm {P} \,dx_{1}'}{2\pi }},\qquad v_{1}={\frac {2\pi z_{1}}{\mathrm {P} }},\\x_{k}&={\frac {d\mathrm {T} }{dy_{k}}},&z_{k}&={\frac {d\mathrm {T} _{1}}{dx_{k}'}}\;\;(i=2,\,3,\,\ldots ,\,n),\;\;(k=1,\,2,\,\ldots ,\,n)\end{aligned}}\right.$

et

(22)

$x_{k}={\frac {d\mathrm {S} }{dy_{k}}}$

sont identiques pourvu que $\mathrm {V}$ satisfasse à l’équation aux dérivées partielles

(23)

$\mathrm {F} ^{\star }\left({\frac {d\mathrm {V} }{dv_{1}}},{\frac {d\mathrm {V} }{dz_{i}}},v_{1},z_{i}\right)=\mathrm {const.} ,$

et à la condition que ses dérivées soient périodiques par rapport a $v_{1}$ et aux $z_{i},$ et que $\mathrm {S}$ soit définie comme au numéro précédent.

$\mathrm {V}$ est développable suivant les puissances de ${\sqrt {\mu }}$ et s’écrit

$\mathrm {V} =\mathrm {V} _{0}+{\sqrt {\mu }}\,\mathrm {V} _{1}+\mu \,\mathrm {V} _{2}+\ldots .$

Chacune des fonctions $\mathrm {V} _{i}$ peut s’écrire

$\mathrm {V} _{i}=\beta _{i}^{1}v_{1}+\beta _{i}^{2}z_{2}+\ldots +\beta _{i}^{n}z_{n}+\mathrm {V} _{i}',$

$\mathrm {V} _{i}'$ étant périodique et les $n$ constantes $\beta _{i}^{k}$ analogues aux constantes $\alpha _{i.k}$ du n^o 125 peuvent comme celles-ci être choisies arbitrairement. On a de même

$\mathrm {S} =\mathrm {S} _{0}+{\sqrt {\mu }}\,\mathrm {S} _{1}+\ldots$

et nous avons vu que $\mathrm {S} _{p}$ dépend encore des constantes arbitraires que nous avons appelées plus haut $\alpha _{i}^{p}.$

Pour que les deux systèmes (21) et (22) soient identiques, il faut, bien entendu, si l’on a donné aux constantes $\beta _{i}^{k}$ des valeurs déterminées, que l’on donne aux constantes $\alpha _{i}^{p}$ des valeurs correspondantes et inversement.

À chaque fonction $\mathrm {V}$ correspond ainsi une fonction $\mathrm {S}$ et réciproquement.

Mais, dans les numéros précédents, nous avons imposé à nos constantes $\alpha _{i}^{p}$ et par conséquent à $\mathrm {S}$ certaines conditions qui sont les hypothèses (9) et (10). Si l’on veut y demeurer astreint, il faut donc que les constantes $\beta _{i}^{k}$ satisfassent de leur côté à certaines conditions qu’il serait aisé de former. Je dirai seulement que les $x_{i}'$ doivent s’annuler avec ${\sqrt {\mu }}.$

Les équations (21) et (22) nous permettant d’exprimer toutes nos variables en fonctions de $n$ quelconques d’entre elles, supposons que l’on exprime $y_{1}$ et les $x_{k}$ en fonctions de

$v_{1},\quad y_{2},\quad y_{3},\quad \ldots ,\quad y_{n}.$

Soit donc

${\begin{aligned}y_{1}&=\theta (v_{1},y_{2},y_{3},\ldots ,y_{n}),\\x_{k}&=\zeta _{k}(v_{1},y_{2},y_{3},\ldots ,y_{n}).\end{aligned}}$

On voit sans peine que les fonctions $\theta$ et $\zeta _{k}$ sont périodiques de période $2\pi$ par rapport à chacune des $n$ variables dont elles dépendent.

Si nous regardons un instant $y_{2},$ $y_{3},$ $\ldots ,\,y_{n}$ comme des constantes et $x_{1}$ et $y_{1}$ comme les coordonnées d’un point dans un plan, nous pourrons envisager les équations

${\begin{aligned}y_{1}&=\theta (v_{1}),&x_{1}&={\frac {d\mathrm {S} }{dy_{1}}}=\zeta _{1}(v_{1}).\end{aligned}}$

Quand nous ferons varier $v_{1},$ le point $x_{1},y_{1}$ décrira une courbe fermée puisque les fonctions $\theta$ et $\zeta _{1}$ reprennent leurs valeurs primitives quand $v_{1}$ augmente de $2\pi .$

Ainsi, si $y_{2},$ $y_{3},$ $\ldots ,\,y_{n}$ sont considérées comme des constantes, l’équation

$x_{1}={\frac {d\mathrm {S} }{dy_{1}}}$

est celle d’une courbe fermée.

C’est là le résultat auquel je voulais parvenir ; mais il importe d’en préciser la signification. Nous ne devons pas oublier, en effet, que tous les théorèmes qui précèdent sont vrais, mais seulement au point de vue du calcul formel.

Les fonctions $\theta$ et $\zeta _{k}$ sont développables suivant les puissances de ${\sqrt {\overset {}{\mu }}},$ de sorte que nous pouvons écrire

(24)

$\left\{{\begin{aligned}y_{1}&=\theta _{0}(v_{1})+{\sqrt {\overset {}{\mu }}}\,\theta _{1}(v_{1})+\mu \,\theta _{2}(v_{1})+\ldots ,\\x_{1}&=\zeta _{1}^{0}(v_{1})+{\sqrt {\overset {}{\mu }}}\,\zeta _{1}^{1}(v_{1})+\mu \,\zeta _{1}^{2}(v_{1})+\ldots ,\end{aligned}}\right.$

et toutes les fonctions $\theta _{p}(v_{1})$ et $\zeta _{1}^{p}(v_{1})$ sont périodiques de période $2\pi .$

Les seconds membres des équations (24) sont des séries ordonnées suivant les puissances de ${\sqrt {\overset {}{\mu }}},$ mais qui, en général, ne sont pas convergentes. Les équations (24) ne sont donc vraies qu’au point de vue du calcul formel. Écrivons donc ces équations de nouveau, mais en nous arrêtant aux termes en $\mu ^{\frac {p}{2}}\,;$ il viendra

(24 bis)

$\left\{{\begin{aligned}y_{1}&=\theta _{0}(v_{1})+\mu ^{\frac {1}{2}}\theta _{1}(v_{1})+\ldots +\mu ^{\frac {p}{2}}\theta _{p}(v_{1}),\\x_{1}&=\zeta _{1}^{0}(v_{1})+\mu ^{\frac {1}{2}}\zeta _{1}^{1}(v_{1})+\ldots +\mu ^{\frac {p}{2}}\zeta _{1}^{p}(v_{1}),\end{aligned}}\right.$

Les équations (24 bis) définissent évidemment une courbe fermée. Supposons qu’éliminant $v_{1}$ entre ces deux équations on les résolve par rapport à $x_{1},$ il viendra

(25)

$x_{1}=\mathrm {P} _{0}+\mu ^{\frac {1}{2}}\mathrm {P} _{1}+\ldots +\mu ^{\frac {q}{2}}\mathrm {P} _{q}+\ldots .$

$\mathrm {P} _{0},\,\mathrm {P} _{1},\,\ldots ,\,\mathrm {P} _{q},\,\ldots$ sont des fonctions de $y_{1}\,;$ le second membre de (25) est une série indéfinie, mais convergente ; et l’équation (25) est celle d’une courbe fermée.

En vertu des principes du calcul formel, la valeur de $x_{1}$ ainsi obtenue ne peut différer de ${\frac {d\mathrm {S} }{dy_{1}}}$ que de quantités de l’ordre de $\mu ^{\frac {p+1}{2}};$ nous aurons donc

${\begin{aligned}\mathrm {P} _{0}&={\frac {d\mathrm {S} _{0}}{dy_{1}}},&\mathrm {P} _{1}&={\frac {d\mathrm {S} _{1}}{dy_{1}}},&&\ldots ,&\mathrm {P} _{p}&={\frac {d\mathrm {S} _{p}}{dy_{1}}},\end{aligned}}$

mais nous n’aurons pas

$\mathrm {P} _{p+1}={\frac {d\mathrm {S} _{p+1}}{dy_{1}}}\cdot$

Maintenant la courbe

(26)

$x_{1}={\frac {d\mathrm {S} _{0}}{dy_{1}}}+\mu ^{\frac {1}{2}}{\frac {d\mathrm {S} _{1}}{dy_{1}}}+\ldots +\mu ^{\frac {p}{2}}{\frac {d\mathrm {S} _{p}}{dy_{1}}}$

est-elle une courbe fermée ?

Reportons-nous à l’équation (15). Comme, dans le cas de la libration, ${\frac {d\mathrm {S} _{1}}{dy_{1}}}$ s’annule pour deux valeurs différentes de $y_{1},$ on peut se demander si ${\frac {d{\big [}\mathrm {S} _{2}{\big ]}}{dy_{1}}}$ et par conséquent ${\frac {d\mathrm {S} _{2}}{dy_{1}}}$ ne pourront pas devenir infinis. Il n’en est rien parce que ${\big [}\Phi {\big ]}$ s’annule en même temps que ${\frac {d\mathrm {S} _{1}}{dy_{1}}}\,;$ mais poussons l’approximation plus loin.

Nous trouverons pour définir ${\frac {d[\mathrm {S} _{3}]}{dy_{1}}}$ une équation analogue à (15)

${\frac {d^{2}\mathrm {F} _{0}}{dx_{1}^{2}}}{\frac {d[\mathrm {S} _{3}]}{dy_{1}}}{\frac {d\mathrm {S} _{1}}{dy_{1}}}={\big [}\Phi {\big ]}+\mathrm {C} _{4}\,;$

${\frac {d[\mathrm {S} _{3}]}{dy_{1}}}$ va-t-il cette fois devenir infini ?

Nous pouvons, il est vrai, disposer de la constante $\mathrm {C} _{4}$ de façon que ${\frac {d\mathrm {S} _{3}}{dy_{1}}}$ ne devienne pas infini pour l’une des valeurs de $y_{1}$ qui annulent ${\frac {d\mathrm {S} _{1}}{dy_{1}}}\,;$ mais, en général, ${\big [}\Phi {\big ]}+\mathrm {C} _{4}$ ne s’annulera pas pour l’autre valeur de $y_{1}$ qui annule ${\frac {d\mathrm {S} _{1}}{dy_{1}}}\,;$ donc ${\frac {d\mathrm {S} _{3}}{dy_{1}}}$ deviendra infini quelle que soit la constante $\mathrm {C} _{4}.$

Ainsi l’équation (26) ne représentera pas une courbe fermée parce que le second membre deviendra infini.

Quand donc j’ai dit plus haut que la courbe

$x_{1}={\frac {d\mathrm {S} }{dy_{1}}}$

est fermée, cette assertion ne pouvait avoir par elle-même aucun sens puisque la série $\mathrm {S}$ est divergente.

Voici ce qu’elle signifiait :

Elle signifiait qu’on peut toujours trouver une fonction $\Phi _{p}$ de $y_{1}$ et de $\mu$ développable suivant les puissances de ${\sqrt {\mu }}$ et telle que l’équation

$x_{1}={\frac {d\mathrm {S} _{0}}{dy_{1}}}+\mu ^{\frac {1}{2}}\,{\frac {d\mathrm {S} _{1}}{dy_{1}}}+\mu \,{\frac {d\mathrm {S} _{2}}{dy_{1}}}+\ldots +\mu ^{\frac {p}{2}}\,{\frac {d\mathrm {S} _{p}}{dy_{1}}}+\mu ^{\frac {p+1}{2}}\,\Phi _{p}$

soit celle d’une courbe fermée.

Un exemple simple fera mieux comprendre ce qui précède.

Soit la courbe

$x={\sqrt {1-y^{2}+\mu \,y^{2}}}.$

C’est une ellipse. Développons le second membre suivant les puissances de $\mu$ et arrêtons le développement, par exemple, aux termes en $\mu ^{2},$ il viendra

$x={\sqrt {1-y^{2}}}+{\frac {\mu }{2}}\,{\frac {y^{2}}{\sqrt {1-y^{2}}}}-{\frac {\mu ^{2}}{8}}\,{\frac {y^{2}}{\left(1-y^{2}\right)^{\frac {3}{2}}}},$

ce qui n’est pas l’équation d’une courbe fermée puisque le second membre devient infini pour $y=\pm 1.$

Toutes ces difficultés, purement artificielles, sont évitées par le changement de variables (16).

Cas limite.

207.Passons enfin au cas où $\mathrm {C} _{2}$ est égal au maximum de ${\big [}\mathrm {F} _{1}{\big ]}$ et qui est intermédiaire entre le cas ordinaire et celui de la libration.

Reprenons les équations (3) du n^o 204 et les équations (13), (14) et (15) du n^o 205. Je suppose toujours $m_{1}=1,$ $m_{i}=0$ (pour $i>1$) et par conséquent $n_{1}^{0}=0.$ Dans ce cas le radical

${\sqrt {c_{2}-{\big [}\mathrm {F} _{1}{\big ]}}}$

${\bigg (}$et par conséquent ${\frac {d\mathrm {S} _{1}}{dy_{1}}}{\bigg )}$ est, comme nous l’avons vu au n^o 200, une fonction périodique de $y_{1},$ mais dont la période n’est plus $2\pi ,$ mais $4\pi .$ Cette fonction change de signe quand on change $y_{1}$ en $y_{1}+2\pi \,;$ elle s’annule pour une seule valeur de $y_{1}$ comprise entre $0$ et $2\pi$ et qui est précisément celle qui fait atteindre à la fonction $[\mathrm {F} _{1}]$ son maximum. On peut, sans restreindre la généralité, supposer que cette valeur est égale à zéro. Alors on aura

${\frac {d\mathrm {S} _{1}}{dy_{1}}}=0$

pour

$y_{1}=2k\pi$

quel que soit l’entier $k.$

J’ai expliqué tout cela en détail au n^o 200.

Considérons maintenant les équations (3) ainsi que les équations analogues à (13) et à (15) que l’on obtient en égalant les valeurs moyennes des deux membres des équations (3). Ces équations nous permettront, ainsi que nous l’avons vu, de déterminer par récurrence les fonctions $\mathrm {S} _{p}$ et elles nous montrent tout d’abord que les ${\frac {d\mathrm {S} _{p}}{dy_{i}}}$ seront des fonctions périodiques des $y,$ la période étant $2\pi$ par rapport à $y_{2},$ $y_{3},$ $\ldots ,\,y_{n}$ et $4\pi$ par rapport à $y_{1}.$

Si les constantes $\mathrm {C} _{p}$ sont nulles, pour un indice $p$ impair, ce que j’ai d’ailleurs supposé en écrivant les équations (3), ces équations (3) ne changeront pas quand on changera $y_{1}$ en $y_{1}+2\pi ,$ ni quand on changera ${\sqrt {\mu }}$ en $-{\sqrt {\mu }}.$

On en déduirait, par un raisonnement tout pareil à celui que j’ai fait au n^o 200, que ${\frac {d\mathrm {S} _{p}}{dy_{i}}}$ se change en

$(-1)^{p}{\frac {d\mathrm {S} _{p}}{dy_{i}}},$

quand $y_{1}$ se change en $y_{1}+2\pi .$

Donc ${\frac {d\mathrm {S} _{p}}{dy_{i}}}$ est une fonction périodique de période $2\pi$ par rapport à $y_{1}$ si $p$ est pair.

Si $p$ est impair, cette fonction change de signe quand $y_{1}$ augmente de $2\pi .$

Maintenant voici la question qui se pose :

Les fonctions ${\frac {d\mathrm {S} _{p}}{dy_{i}}}$ sont-elles finies ?

Nous avons pour déterminer ${\big [}\mathrm {S} _{2}{\big ]}$ l’équation (15)

${\frac {d^{2}\mathrm {F} _{0}}{dx_{1}^{2}}}\,{\frac {d[\mathrm {S} _{2}]}{dy_{1}}}\,{\frac {d\mathrm {S} _{1}}{dy_{1}}}={\big [}\Phi {\big ]},$

et plus généralement pour déterminer ${\big [}\mathrm {S} _{p}{\big ]}$

(27)

${\frac {d^{2}\mathrm {F} _{0}}{dx_{1}^{2}}}\,{\frac {d[\mathrm {S} _{p}]}{dy_{1}}}\,{\frac {d\mathrm {S} _{1}}{dy_{1}}}={\big [}\Phi {\big ]}+\mathrm {C} _{p+1},$

$\mathrm {C} _{p+1}$ étant nul quand $p+1$ est impair.

La fonction ${\big [}\Phi {\big ]}$ du second membre de (27) dépendant seulement de $y_{1},$ je la poserai égale à $\varphi _{p+1}(y_{1}).$

On verrait aisément par récurrence que

$\varphi _{p+1}(y_{1}+2\pi )=(-1)^{p+1}\varphi _{p+1}(y_{1}).$

Il pourrait arriver que ${\frac {d[\mathrm {S} _{p}]}{dy_{1}}}$ devînt infini ; car ${\frac {d\mathrm {S} _{1}}{dy_{1}}}$ peut s’annuler pour $y_{1}=2k\pi$ et il pourrait se faire que pour cette valeur de $y_{1}$ le second membre de (27) ne s’annulât pas.

Si nous voulons donc que les ${\frac {d[\mathrm {S} _{p}]}{dy_{1}}}$ demeurent finies, il faut donc que

(28)

$\varphi _{p+1}(0)+\mathrm {C} _{p+1}=\varphi _{p+1}(2\pi )=\mathrm {C} _{p+1}=0.$

Si les conditions (28) sont remplies par toutes les valeurs de $p,$ les ${\frac {d[\mathrm {S} _{p}]}{dy_{1}}}$ et par conséquent aussi les ${\frac {d\mathrm {S} _{p}}{dy_{1}}}$ resteront finis.

Si $p+1$ est pair, on satisfera facilement aux équations (28) ; la constante $\mathrm {C} _{p+1}$ est en effet arbitraire et il suffira de la prendre égale à

$-\varphi _{p+1}(0)=-\varphi _{p+1}(2\pi ).$

Mais, si $p+1$ est impair, $\mathrm {C} _{p+1}$ est nul et nous devons satisfaire à la condition

(29)

$\varphi _{p+1}(0)=0$

qui entraîne d’ailleurs la suivante

$\varphi _{p+1}(2\pi )=0.$

Comme nous ne disposons plus d’aucune arbitraire, cette condition (29) doit être remplie d’elle-même ; c’est en effet ce qui arrive, mais cela exige une démonstration spéciale que je vais donner dans les numéros suivants.

208.Supposons d’abord qu’il n’y ait que deux degrés de liberté et par conséquent quatre variables seulement $x_{1},$ $x_{2},$ $y_{1}$ et $y_{2}.$

Reportons-nous aux n^os 42, 43 et 44 ; nous y avons vu qu’à chaque système de valeurs des moyens mouvements

$n_{1}^{0},\quad n_{2}^{0},\quad \ldots ,\quad n_{n}^{0}$

qui soient commensurables entre elles, correspond une fonction $[\mathrm {F} _{1}]$ et qu’à chaque maximum ou à chaque minimum de cette fonction correspond une solution périodique.

Or, dans le cas qui nous occupe, les moyens mouvements sont au nombre de deux

$n_{1}^{0},\quad n_{2}^{0},$

et l’un d’eux $n_{1}^{0}$ est nul ; les valeurs des deux moyens mouvements sont donc commensurables entre elles. De plus la fonction ${\big [}\mathrm {F} _{1}{\big ]}$ admet un maximum absolu qu’elle atteint pour $y_{1}=0$ et qui est égal à $\mathrm {C} _{2}.$ À ce maximum doit donc correspondre une solution périodique. Soit

(30)

${\begin{aligned}x_{1}&=\psi _{1}(t),&x_{2}&=\psi _{2}(t),&y_{1}&=\psi _{1}'(t),&y_{2}&=\psi _{2}'(t)\end{aligned}}$

cette solution. Comme $n_{1}^{0}$ est nul, quand $t$ augmente d’une période, $\psi _{1},$ $\psi _{2}$ et $\psi _{1}'$ reprennent leurs valeurs primitives, tandis que $y_{2}$ augmente de $2\pi .$

Si nous éliminons $t$ entre les équations (30), il vient

(31)

${\begin{aligned}x_{1}&=\theta _{1}(y_{2}),&x_{2}&=\theta _{2}(y_{2}),&y_{1}&=\theta _{3}(y_{2}),\end{aligned}}$

les fonctions $\theta$ étant périodiques de période $2\pi .$

Les exposants caractéristiques sont au nombre de deux et d’après le Chapitre IV doivent être égaux et de signe contraire. De plus, comme la solution périodique correspond à un maximum et non à un minimum de $[\mathrm {F} _{1}],$ ces exposants doivent être réels, en vertu du n^o 79, et la solution périodique doit être instable.

Cela posé, nous allons faire un changement de variables analogue à celui du n^o 145.

Soit

$\mathrm {S} ^{\star }=x_{2}'y_{2}+\Theta +x_{1}'y_{1}+y_{1}\theta _{1}-x_{1}'\theta _{3},$

où $\Theta$ est une fonction de $y_{2}$ définie par la condition

${\frac {d\Theta }{dy_{2}}}=\theta _{2}-\theta _{3}\,{\frac {d\theta _{1}}{dy_{2}}}\cdot$

La forme canonique des équations ne sera pas altérée si je prends pour variables nouvelles $x_{i}'$ et $y_{i}'$ en posant

${\begin{aligned}x_{i}&={\frac {d\mathrm {S} ^{\star }}{dy_{i}}},&y_{i}'&={\frac {d\mathrm {S} ^{\star }}{dx_{i}'}}\cdot \end{aligned}}$

On trouve ainsi

(32)

$\left\{{\begin{aligned}x_{1}&=x_{1}'+\theta _{1};&x_{2}&=x_{2}'+{\frac {d\Theta }{dy_{2}}}+y_{1}\,{\frac {d\theta _{1}}{dy_{2}}}-x_{1}'\,{\frac {d\theta _{3}}{dy_{2}}}\\y_{1}'&=y_{1}-\theta _{3};&y_{2}'&=y_{2},\end{aligned}}\right.$

d’où

$x_{2}=x_{2}'+\theta _{2}+y_{1}'\,{\frac {d\theta _{1}}{dy_{2}}}-x_{1}'\,{\frac {d\theta _{3}}{dy_{2}}}\cdot$

Quelle sera la forme de la fonction $\mathrm {F}$ exprimée à l’aide des nouvelles variables ?

Observons d’abord que $\theta _{1},$ $\theta _{2}$ et $\theta _{3}$ sont, en vertu des n^os 42 à 44, développables suivant les puissances croissantes de $\mu$ et que, pour $\mu =0,$ elles se réduisent à des constantes

$x_{1}^{0},\quad x_{2}^{0}$et$0.$

On voit ainsi que $x_{1},$ $y_{1}$ et $x_{2}$ sont des fonctions de $x_{1}',$ $x_{2}',$ $y_{1}'$ et $y_{2}'$ et de $\mu ,$ développables suivant les puissances de $\mu$ et périodiques par rapport à $y_{2}'.$ Pour $\mu =0,$ elles se réduisent à

${\begin{aligned}x_{1}&=x_{1}'+x_{1}^{0},&x_{2}&=x_{2}'+x_{2}^{0},&y_{1}&=y_{1}'.\end{aligned}}$

Donc $\mathrm {F}$ conserve la même forme quand on l’exprime en fonction des variables nouvelles : je veux dire que $\mathrm {F}$ est développable suivant les puissances de $\mu ,$ et périodique par rapport à $y_{2}',$ mais $\mathrm {F}$ n’est pas périodique par rapport à $y_{1}'.$

Les nouvelles équations canoniques

${\begin{aligned}{\frac {dx_{i}'}{dt}}&={\frac {d\mathrm {F} }{dy_{i}'}},&{\frac {dy_{i}'}{dt}}&=-{\frac {d\mathrm {F} }{dx_{i}'}},\end{aligned}}$

admettent évidemment pour solution

$x_{1}'=0,\qquad x_{2}'=0,\qquad y_{1}'=0,$

puisque les anciennes admettaient

$x_{1}=\theta _{1},\qquad x_{2}=\theta _{2},\qquad y_{1}=\theta _{3}.$

Nous en concluons que les trois dérivées

${\frac {d\mathrm {F} }{dy_{1}'}},\quad {\frac {d\mathrm {F} }{dy_{2}'}},\quad {\frac {d\mathrm {F} }{dx_{1}'}}$

s’annulent à la fois quand on y fait

$x_{1}'=x_{2}'=y_{1}'=0.$

D’autre part, quand on fait $x_{1}'=x_{2}'=y_{1}'=0,$ $\mathrm {F}$ se réduit à une constante que j’appellerai $\mathrm {A}$ et qui est d’ailleurs développable suivant les puissances de $\mu .$

Posons

$\mathrm {F} '=\mathrm {F} -\mathrm {A} \,;$

$\mathrm {F} '$ sera développable suivant les puissances de $x_{1}',$ $x_{2}'$ et $y_{1}'$ pour les petites valeurs de ces variables ; le développement ne contiendra pas de terme de degré 0, et il ne contiendra d’autre terme du premier degré qu’un terme en $x_{2}'.$ Les coefficients du développement sont des fonctions de $\mu$ et de $y_{2}'.$

Considérons alors l’équation

$\mathrm {F} '\left({\frac {d\mathrm {S} '}{dy_{1}'}},\,{\frac {d\mathrm {S} '}{dy_{2}'}},\,y_{1}',\,y_{2}'\right)=0\,;$

cherchons à y satisfaire en faisant

(33)

$\mathrm {S} '=\mathrm {S} _{0}'+{\sqrt {\mu }}\,\mathrm {S} _{1}'+\mu \,\mathrm {S} _{2}'+\ldots .$

Nous déterminerons par récurrence les fonctions $\mathrm {S} _{p}'$ à l’aide d’équations tout à fait analogues aux équations (3) du n^o 204 et qui n’en diffèrent que parce que les lettres y sont accentuées et que les constantes $\mathrm {C} _{p}$ sont toutes nulles.

Remplaçons dans $\mathrm {F} '$ la fonction $\mathrm {S} '$ par sa valeur (33) et développons ensuite $\mathrm {F} '$ suivant les puissances croissantes de ${\sqrt {\mu }}.$

Soit

$\mathrm {F} '=\psi _{0}+{\sqrt {\mu }}\,\psi _{1}+\mu \,\psi _{2}+\ldots$

ce développement. Alors $\psi _{p}$ va, pour les petites valeurs de $y_{1}',$ $x_{1}'$ et $x_{2}',$ être développable suivant les puissances de $y_{1}',$ des ${\frac {d\mathrm {S} _{q}'}{dy_{1}'}},$ des ${\frac {d\mathrm {S} _{q}'}{dy_{2}'}}\cdot$

Les coefficients du développement seront des fonctions périodiques de $y_{2}'\,;$ mais le point sur lequel je veux attirer l’attention, c’est que le développement ne contiendra pas de terme de degré 0 et que les seuls termes du premier degré seront des termes en

${\frac {d\mathrm {S} _{q}'}{dy_{2}'}}\cdot$

Nous allons donc avoir à déterminer

$\mathrm {S} _{q}'-{\big [}\mathrm {S} _{q}'{\big ]}$

par des équations

(34)

$n_{2}^{0}\,{\frac {d\mathrm {S} _{q}'}{dy_{2}'}}=\Phi$

analogues à (14) et à déterminer ${\big [}\mathrm {S} _{q}'{\big ]}$ par des équations

(35)

${\frac {d^{2}\mathrm {F} _{0}'}{dx_{1}'^{2}}}\,{\frac {d[\mathrm {S} _{q}']}{dy_{1}'}}\,{\frac {d\mathrm {S} _{1}'}{dy_{1}'}}={\big [}\Phi '{\big ]}.$

analogues à (15), les constantes analogues aux $\mathrm {C} _{p}$ étant toutes nulles.

Les fonctions $\Phi$ et $\Phi '$ qui entrent dans les seconds membres de (34) et de (35) peuvent être développées suivant les puissances de $y_{1}',$ ${\frac {d\mathrm {S} _{i}'}{dy_{1}'}},$ ${\frac {d\mathrm {S} _{i}'}{dy_{2}'}}$ et les seuls termes du premier degré sont des termes en ${\frac {d\mathrm {S} _{i}'}{dy_{2}'}}\cdot$

Je dis que non seulement la valeur $y_{1}'=0$ n’est pas un infini pour les ${\frac {d\mathrm {S} _{i}'}{dy_{2}'}}$ et les ${\frac {d\mathrm {S} _{i}'}{dy_{1}'}},$ mais que c’est un zéro, a savoir un zéro simple pour les ${\frac {d\mathrm {S} _{i}'}{dy_{1}'}}$ et un zéro double pour les ${\frac {d\mathrm {S} _{i}'}{dy_{2}'}}\cdot$

En effet, démontrons ce théorème par récurrence et supposons qu’il soit déjà vrai pour les fonctions déjà connues.

Alors la fonction $\Phi$ de l’équation (34) admettra la valeur $y_{1}'=0$ comme zéro double ; et en effet cette valeur est un zéro simple pour chacun des facteurs des termes de degré plus grand que 1 du développement de $\Phi$ suivant les puissances de $y_{1}',$ des ${\frac {d\mathrm {S} _{i}'}{dy_{1}'}}$ et des ${\frac {d\mathrm {S} _{i}'}{dy_{2}'}}\,;$ et d’autre part les termes du premier degré de ce développement dépendent des dérivées ${\frac {d\mathrm {S} _{i}'}{dy_{2}'}}$ pour lesquelles $y_{1}'=0$ est un zéro double.

Il résulte de là et de l’équation (34) que $y_{1}'=0$ est un zéro double pour

${\frac {d\mathrm {S} _{q}'}{dy_{2}'}},$

et par conséquent pour

$\mathrm {S} _{q}'-{\big [}\mathrm {S} _{q}'{\big ]},$

et un zéro simple pour

${\frac {d\mathrm {S} _{q}'}{dy_{1}'}}-{\frac {d[\mathrm {S} _{q}']}{dy_{1}'}}\cdot$

On pourrait ensuite raisonner sur la fonction $\Phi '$ de l’équation (35) comme on vient de le faire sur la fonction $\Phi$ et l’on verrait ainsi que $y_{1}'=0$ est un zéro double pour $\Phi '$ et par conséquent pour ${\big [}\Phi '{\big ]}.$

Comme, d’autre part, c’est un zéro simple pour ${\frac {d\mathrm {S} _{i}'}{dy_{1}'}},$ ce sera également un zéro simple pour

${\frac {d[\mathrm {S} _{q}']}{dy_{1}'}}\cdot$

C.Q.F.D.

Ainsi les fonctions définies par les équations (34) et (35) sont finies.

Quelle relation y a-t-il maintenant entre la fonction $\mathrm {S}$ définie au numéro précédent et la fonction $\mathrm {S} '$ que nous venons de déterminer ?

Nous avons

${\begin{aligned}d\mathrm {S} \,&=x_{1}dy_{1}+x_{2}dy_{2},\\d\mathrm {S} '&=x_{1}'dy_{1}'+x_{2}'dy_{2}',\end{aligned}}$

d’où, en tenant compte des équations (32),

$d\mathrm {S} '-d\mathrm {S} =d\Theta -d(y_{1}\theta _{1}),$

d’où

(36)

$\mathrm {S} '-\mathrm {S} =\Theta -y_{1}\theta _{1}.$

Comme $\mathrm {S} ',$ $\Theta$ et $\theta _{1}$ sont toujours finis ainsi que leurs dérivées, il en sera de même de $\mathrm {S}$ et de ses dérivées.

Il est aisé, en égalant dans (36) les coefficients des puissances semblables de ${\sqrt {\mu }},$ de calculer les fonctions $\mathrm {S} _{p}.$

En effet, nous avons écrit plus haut

(33)

$\mathrm {S} '=\mathrm {S} _{0}'+{\sqrt {\mu }}\,\mathrm {S} _{1}'+\mu \,\mathrm {S} _{2}'+\ldots ,$

mais ce développement est obtenu en supposant que les $S_{p}'$ sont exprimés en fonctions des variables nouvelles $x_{i}'$ et $y_{i}'\,;$ si l’on revient aux variables anciennes $x_{i}$ et $y_{i},$ le développement change de forme et s’écrit

$\mathrm {S} '=\mathrm {S} _{0}''+{\sqrt {\mu }}\,\mathrm {S} _{1}''+\mu \,\mathrm {S} _{2}''+\ldots$

[cf. les équations (8) du n^o 200].

Soit de même

${\begin{aligned}\Theta &={\textstyle \sum }\,\mu ^{\frac {p}{2}}\Theta _{p},&\theta _{1}&={\textstyle \sum }\,\mu ^{\frac {p}{2}}\theta _{1}^{p}.\end{aligned}}$

Nous aurons alors

(36′)

$\mathrm {S} _{p}=\mathrm {S} _{p}''-\Theta _{p}+y_{1}\theta _{1}^{p},$

équation qui nous montre que l’on peut choisir les constantes $\mathrm {C} _{p+1}$ de telle sorte que1 les ${\frac {d\mathrm {S} _{p}}{dy_{i}}}$ restent constamment finis.

D’où nous devons conclure que les conditions (29) sont remplies d’elles-mêmes.

Nous avons vu au numéro précédent que les ${\frac {d\mathrm {S} _{p}}{dy_{i}}}$ sont des fonctions périodiques de période $4\pi$ par rapport à $y_{1}\,;$ il n’en est pas de même ici des ${\frac {d\mathrm {S} _{p}'}{dy_{i}'}}$ ni des ${\frac {d\mathrm {S} _{p}''}{dy_{i}}},$ parce que $\mathrm {F} ,$ comme je l’ai fait observer plus haut, n’est plus périodique en $y_{1}'.$ Cependant l’équation (36′) nous montre :

1^o Que ${\frac {d\mathrm {S} _{p}''}{dy_{1}}}$ est périodique ;

2^o Que ${\frac {d\mathrm {S} _{p}''}{dy_{2}}}$ augmente de $-4\pi \theta _{1}^{p}$ quand $y_{1}$ augmente de $4\pi .$

Considérons les équations

(37)

${\begin{aligned}x_{1}&={\frac {d\mathrm {S} }{dy_{1}}},&x_{2}&={\frac {d\mathrm {S} }{dy_{2}}}\end{aligned}}$

qui nous donnent $x_{1}$ et $x_{2}$ en fonctions de $y_{1}$ et de $y_{2}.$ Elles ont une signification intéressante.

Reprenons, en effet, les équations (30) ; elles définissent la solution périodique qui nous a servi de point de départ. Nous avons vu que cette solution est instable.

Donc, en vertu des principes du Chapitre VII, elle donne naissance à deux séries de solutions asymptotiques, dont les équations générales peuvent être mises sous la forme

(38)

$\;{\begin{aligned}x_{1}&=\omega _{1}(t,\mathrm {A} ),&x_{2}&=\omega _{2}(t,\mathrm {A} ),&y_{1}&=\omega _{1}'(t,\mathrm {A} ),&y_{2}&=\omega _{2}'(t,\mathrm {A} )\end{aligned}}$

pour la première série ou

(39)

$\;{\begin{aligned}x_{1}&=\eta _{1}(t,\mathrm {B} ),&x_{2}&=\eta _{2}(t,\mathrm {B} ),&y_{1}&=\eta _{1}'(t,\mathrm {B} ),&y_{2}&=\eta _{2}'(t,\mathrm {B} )\end{aligned}}$

pour la seconde.

$\mathrm {A}$ et $\mathrm {B}$ sont des constantes arbitraires.

Si entre les équations (38) on élimine $t$ et $\mathrm {A} ,$ puis qu’on résolve par rapport à $x_{1}$ et $x_{2},$ on obtiendra les équations (37) et l’on obtiendra encore le même résultat ${\big (}$le signe du radical ${\sqrt {\mathrm {C} _{2}-{\big [}\mathrm {F} _{1}{\big ]}}}$ étant seul changé${\big )}$ si l’on élimine $t$ et $\mathrm {B}$ entre les équations (39).

Il peut être intéressant de comparer la démonstration qui précède celles que j’avais données dans le Tome XIII des Acta mathematica, p. 211 à 216 d’une part, 217 à 219 d’autre part.

209.Occupons-nous d’étendre cette démonstration au cas où il y a plus de deux degrés de liberté et, pour cela, cherchons d’abord à généraliser la notion qui nous a servi de point de départ, c’est-à-dire celle de la solution périodique (30).

Cherchons donc $n+1$ fonctions des $n-1$ variables

$y_{2},\quad y_{3},\quad \ldots ,\quad y_{n},$

fonctions que j’appellerai

$\eta ,\quad \zeta ,\quad \xi _{2},\quad \xi _{3},\quad \ldots ,\quad \xi _{n}$

et qui seront telles que les relations

${\begin{aligned}x_{1}&=\eta ,&y_{1}&=\zeta ,&x_{i}&=\xi _{i}\quad (i>1)\end{aligned}}$

soient des relations invariantes au sens donné à ce mot au n^o 19. Cela entraîne les conditions suivantes

(40)

$\left\{{\begin{alignedat}{3}{\sum }_{k}{\frac {d\eta }{dy_{k}}}\,{\frac {d\mathrm {F} }{dx_{k}}}&={}&-&{\frac {d\mathrm {F} }{dy_{1}}},\\{\sum }_{k}{\frac {d\xi _{i}}{dy_{k}}}\,{\frac {d\mathrm {F} }{dx_{k}}}&={}&-&{\frac {d\mathrm {F} }{dy_{i}}},\\{\sum }_{k}{\frac {d\zeta }{dy_{k}}}\,{\frac {d\mathrm {F} }{dx_{k}}}&={}&&{\frac {d\mathrm {F} }{dx_{i}}}\quad (i,\,k=2,\,3,\,\ldots ,\,n).\end{alignedat}}\right.$

Inutile d’ajouter que, dans les dérivées de $\mathrm {F} ,$ $x_{1},$ $y_{1}$ et les $x_{i}$ sont supposés remplacés par $\eta ,$ $\zeta$ et les $\xi _{i}.$

De plus, les fonctions $\eta ,$ $\zeta$ et $\xi _{i}$ doivent être périodiques en $y_{2},$ $y_{3},$ $\ldots ,\,y_{n}\,;$ elles devront se réduire à des constantes $\eta _{0},$ $\zeta _{0}$ et $\xi _{i}^{0}$ pour $\mu =0.$

Enfin je m’impose une condition de plus, je veux que

$x_{1}\,dy_{1}+x_{2}\,dy_{2}+\ldots +x_{n}\,dy_{n}=d\theta +\eta _{0}\,d\zeta$

soit la différentielle exacte d’une fonction $\theta +\eta _{0}\zeta$ de $y_{2},$ $y_{3},$ $\ldots ,\,y_{n}.$ On en tire

(41)

$\xi _{i}={\frac {d\theta }{dy_{i}}}-(\eta -\eta _{0}){\frac {d\zeta }{dy_{i}}},$

et l’on en conclut que les dérivées de $\theta$ sont des fonctions périodiques. On aura de plus

(42)

$\mathrm {F} (\eta ,\xi _{i},\zeta ,y_{i})=\mathrm {const.} ,$

c’est-à-dire qu’en remplaçant dans $\mathrm {F}$ les variables $x_{1},$ $x_{i}$ et $y_{1}$ par les fonctions $\eta ,$ $\xi _{i}$ et $\zeta ,$ on réduit $\mathrm {F}$ à une constante.

On vérifierait aisément par un calcul qui rappelle quelques-uns de ceux du Chapitre XV que la deuxième équation (40) est une conséquence nécessaire des deux autres et des équations (41) et (42).

Si, en effet, on différentie l’équation (42) par rapport à $y_{k},$ et qu’on la transforme ensuite en tenant compte de la première et de la troisième équation (40) ainsi que des relations

${\frac {dx_{i}}{dy_{k}}}+{\frac {dy_{1}}{dy_{k}}}{\frac {dx_{1}}{dy_{i}}}={\frac {dx_{k}}{dy_{i}}}+{\frac {dy_{1}}{dy_{i}}}{\frac {dx_{1}}{dy_{k}}}$

déduites des relations (41) par différentiation, on retrouvera la seconde équation (40).

Nous conserverons donc, pour définir les fonctions $\eta ,$ $\zeta ,$ $\xi _{i}$ et $\theta ,$ la première et la troisième équation (40) ainsi que les équations (41) et (42).

Nous allons chercher à développer les fonctions $\eta ,$ $\zeta$ et $\theta$ suivant les puissances de $\mu ,$ sous la forme

(43)

$\left\{{\begin{aligned}\eta &=\eta _{0}+\mu \,\eta _{1}+\mu ^{2}\,\eta _{2}+\ldots ,\\\zeta &=\zeta _{0}+\mu \,\zeta _{1}+\mu ^{2}\,\zeta _{2}+\ldots ,\\\theta &=\theta _{0}+\mu \,\theta _{1}+\mu ^{2}\,\theta _{2}+\ldots ;\qquad \xi _{i}={\textstyle \sum }\,\mu ^{p}\xi _{i}^{p}\end{aligned}}\right.$

Nous trouvons d’abord, en faisant $\mu =0$ dans la première équation (40)

${\textstyle \sum }\,n_{k}^{0}\,{\frac {d\eta _{0}}{dy_{k}}}=0,$

ce qui prouve d’abord que $\eta _{0}$ ne dépend pas de $y_{2},$ $y_{3},$ $\ldots ,\,y_{n},$ ce que nous pouvons écrire

$\eta _{0}={\big [}\eta _{0}{\big ]},$

puisque $[\eta _{0}]$ désigne la valeur moyenne de $\eta _{0}$ considérée comme fonction périodique de $y_{2},$ $y_{3},$ $\ldots ,\,y_{n}.$

Il vient ensuite, en faisant $\mu =0$ dans la troisième équation (40),

$-{\textstyle \sum }\,n_{k}^{0}\,{\frac {d\zeta _{0}}{dy_{k}}}={\frac {d\mathrm {F} _{0}}{dx_{1}}}\cdot$

Dans le second membre $x_{1}$ et les $x_{i}$ doivent être respectivement remplacés par $\eta _{0}$ et $\xi _{i}^{0},$ et ces quantités doivent être des constantes telles que l’on ait

${\begin{aligned}{\frac {d\mathrm {F} _{0}}{dx_{1}}}&=-n_{1}^{0}=0,&{\frac {d\mathrm {F} _{0}}{dx_{i}}}&=-n_{i}^{0}.\end{aligned}}$

Nous regarderons les $n_{i}^{0}$ comme des données de la question de telle façon que ces équations détermineront les $\xi _{i}^{0}$ et

$\eta _{0}={\big [}\eta _{0}{\big ]}.$

Notre équation devient alors

${\textstyle \sum }\,n_{k}^{0}\,{\frac {d\zeta _{0}}{dy_{k}}}=0,$

d’où

$\zeta _{0}={\big [}\zeta _{0}{\big ]}.$

Comme $\eta _{0}$ est une constante absolue, et que ${\frac {d\zeta _{0}}{dy_{k}}}$ doit être nul, les équations (41) nous donneront

$\xi _{i}^{0}={\frac {d\theta _{0}}{dy_{i}}}\cdot$

Si, d’autre part, nous développons la constante du second membre de (42) suivant les puissances croissantes de $\mu$ et que nous l’écrivions

$\mathrm {C} _{0}+\mathrm {C} _{1}\mu +\mathrm {C} _{2}\mu ^{2}+\ldots ,$

l’équation (42), quand nous y ferons $\mu =0,$ nous donnera

$\mathrm {F} _{0}\left(\eta _{0},{\frac {d\theta _{0}}{dy_{1}}}\right)=\mathrm {C} _{0}.$

Cette équation détermine simplement la constante $\mathrm {C} _{0},$ et nous voyons de plus que

$\theta _{0}=\xi _{2}^{0}y_{2}+\xi _{3}^{0}y_{3}+\ldots +\xi _{n}^{0}y_{n}.$

Nous connaissons maintenant $\eta _{0}$ et $\theta _{0}\,;$ mais, quant à $\zeta _{0},$ nous savons seulement que $\zeta _{0}$ est une constante et par conséquent que

$\zeta _{0}={\big [}\zeta _{0}{\big ]},$

mais nous ne connaissons pas ${\big [}\zeta _{0}{\big ]}.$

Égalons les coefficients de $\mu$ dans la première équation (40), il viendra, si l’on se rappelle que $\eta _{0}$ est une constante,

${\textstyle \sum }\,n_{k}^{0}\,{\frac {d\eta _{1}}{dy_{k}}}={\frac {d\mathrm {F} _{1}}{dy_{1}}}\cdot$

Dans le second membre $y_{1},$ $x_{1}$ et les $x_{i}$ sont supposés remplacés par $\zeta _{0},$ $\eta _{0}$ et les $\xi _{i}^{0}\,;$ ce second membre sera une fonction périodique de $y_{2},$ $y_{3},$ $\ldots ,\,y_{n},$ et sa valeur moyenne, puisque $\zeta _{0},$ $\eta _{0},$ $\xi _{i}^{0}$ sont des constantes, sera

$\left[{\frac {d\mathrm {F} _{1}}{dy_{1}}}\right]={\frac {d[\mathrm {F} _{1}]}{dy_{1}}}\cdot$

Cette valeur moyenne doit être nulle, ce qui donne une équation

${\frac {d[\mathrm {F} _{1}]}{dy_{1}}}=0$

qui détermine la constante $\zeta _{0}.$

Il reste alors

${\textstyle \sum }\,n_{k}^{0}\;{\frac {d\eta _{1}}{dy_{k}}}=\Phi ,$

$\Phi$ étant une fonction périodique connue dont la valeur moyenne est nulle, équation d’où l’on tire aisément

$\eta _{1}-{\big [}\eta _{1}{\big ]}.$

Égalons maintenant les coefficients $\mu$ dans l’équation (42) en tenant compte des équations (41), qui nous donnent

$\xi _{i}^{1}={\frac {d\theta _{1}}{dy_{i}}}-\eta _{1}\,{\frac {d\zeta _{0}}{dy_{i}}}={\frac {d\theta _{1}}{dy_{i}}}\,;$

nous trouverons

${\textstyle \sum }\,n_{k}^{0}\,{\frac {d\theta _{1}}{dy_{k}}}=\Phi -\mathrm {C} _{1}.$

$\Phi$ est une fonction périodique connue dont la valeur moyenne n’a pas besoin d’être nulle, puisque nous n’avons pas assujetti $\theta _{1},$ mais seulement ses dérivées, à être périodiques. Cette équation nous donnera $\theta _{1}$ qui dépendra de $n-1$ constantes que nous pourrons choisir arbitrairement.

Égalons les coefficients de $\mu$ dans la troisième équation (40), il viendra

(44)

${\textstyle \sum }\,n_{k}^{0}\,{\frac {d\zeta _{1}}{dy_{k}}}=\Phi -{\frac {d^{2}\mathrm {F} _{0}}{dx_{1}^{2}}}\,\eta _{1}.$

La valeur moyenne du second membre doit être nulle, d’où

${\frac {d^{2}\mathrm {F} _{0}}{dx_{1}^{2}}}{\big [}\eta _{1}{\big ]}={\big [}\Phi {\big ]},$

ce qui nous donne ${\big [}\eta _{1}{\big ]}$ et l’équation (44) nous donne ensuite

$\zeta _{1}-{\big [}\zeta _{1}{\big ]}.$

Continuons de la même manière et supposons que l’on ait trouvé

${\begin{array}{c}\eta _{0},\quad \eta _{1},\quad \ldots ,\quad \eta _{p-1},\quad \theta _{0},\quad \theta _{1},\quad \ldots ,\quad \theta _{p-1},\\\zeta _{0},\quad \zeta _{1},\quad \ldots ,\,\zeta _{p-2},\quad \zeta _{p-1}-{\big [}\zeta _{p-1}{\big ]},\end{array}}$

et qu’on se propose de trouver

$\eta _{p},\quad \theta _{p},$et$\zeta _{p-1},\quad \zeta _{p}-{\big [}\zeta _{p}{\big ]}.$

Égalons d’abord les coefficients de $\mu ^{p}$ dans la troisième équation (40), il viendra

(45)

${\textstyle \sum }\,n_{k}^{0}\,{\frac {d\eta _{p}}{dy_{k}}}=\Phi +{\frac {d^{2}\mathrm {F} _{1}}{dy_{1}^{2}}}\zeta _{p-1}.$

Le second membre doit avoir sa valeur moyenne nulle, d’où

$\left[{\frac {d^{2}\mathrm {F} _{1}}{dy_{1}^{2}}}\zeta _{p-1}\right]={\big [}\Phi {\big ]}$

ou

${\frac {d^{2}[\mathrm {F} _{1}]}{dy_{1}^{2}}}\zeta _{p-1}=\Phi -\left[{\frac {d^{2}\mathrm {F} _{1}}{dy_{1}^{2}}}\left(\zeta _{p-1}-{\big [}\zeta _{p-1}{\big ]}\right)\right]$

d’où nous tirerons ${\big [}\zeta _{p-1}{\big ]}$ puisque $\zeta _{p-1}-{\big [}\zeta _{p-1}{\big ]}$ est connu. Donc $\zeta _{p-1}$ est désormais connu, et l’équation (45) nous donne

$\eta _{p}-{\big [}\eta _{p}{\big ]}.$

Si nous égalons maintenant les coefficients de $\mu ^{p}$ (42), en tenant compte de (41), il viendra

${\textstyle \sum }\,n_{k}^{0}\,{\frac {d\theta _{p}}{dy_{k}}}=\Phi -\mathrm {C} _{p},$

d’où nous tirerons $\theta _{p}.$

Égalant, enfin les coefficients de $\mu ^{p}$ dans la troisième équation (40), nous trouvons une équation analogue à (44)

(46)

${\textstyle \sum }\,n_{k}^{0}\,{\frac {d\zeta _{p}}{dy_{k}}}=\Phi -{\frac {d^{2}\mathrm {F} _{0}}{dx_{1}^{2}}}\,\eta _{p}.$

Le second membre doit avoir sa valeur moyenne nulle et cette condition

$\Phi ={\frac {d^{2}\mathrm {F} _{0}}{dx_{1}^{2}}}\,{\big [}\eta _{p}{\big ]}$

détermine ${\big [}\eta _{p}{\big ]}$ et par conséquent $\eta _{p}.$

L’équation (46) détermine ensuite

$\zeta _{p}-{\big [}\zeta _{p}{\big ]}$

et ainsi de suite.

Nous avons donc pu déterminer des fonctions satisfaisant aux conditions que nous nous étions imposées et nous avons ainsi réalisé une véritable généralisation des solutions périodiques. Seulement, tandis que les séries qui définissent les solutions périodiques sont convergentes, il n’en est plus de même de celles dont nous venons de démontrer l’existence, de sorte que cette généralisation n’a de valeur qu’au point de vue du calcul formel.

210.Cherchons maintenant à nous servir des résultats du numéro précédent pour démontrer dans le cas général que les relations (29) sont satisfaites d’elles-mêmes.

À cet effet, posons

$\mathrm {S} ^{\star }=x_{2}'y_{2}+x_{3}'y_{3}+\ldots +x_{n}'y_{n}+\theta -(\eta -\eta _{0})\zeta +x_{1}'y_{1}+y_{1}\eta -x_{1}'\zeta$

et changeons de variables en posant

${\begin{aligned}x_{i}&={\frac {d\mathrm {S} ^{\star }}{dy_{i}}},&y_{i}'&={\frac {d\mathrm {S} ^{\star }}{dx_{i}'}},\end{aligned}}$

la forme canonique des équations ne sera pas altérée, et l’on trouvera

${\begin{aligned}x_{1}&=x_{1}'+\eta ,&y_{1}'&=y_{1}-\zeta ,&y_{i}'&=y_{i}\quad (i>1),\end{aligned}}$

et enfin

$x_{i}=x_{i}'+{\frac {d\theta }{dy_{i}}}-(\eta -\eta _{0}){\frac {d\zeta }{dy_{i}}}+y_{1}\,{\frac {d\eta }{dy_{i}}}-x_{1}'\,{\frac {d\zeta }{dy_{i}}},$

ou, en tenant compte de (41),

$x_{i}=x_{i}'+\xi _{i}+y_{1}'\,{\frac {d\eta }{dy_{i}}}-x_{1}'\,{\frac {d\zeta }{dy_{i}}}\cdot$

$\mathrm {F}$ conserve la même forme avec les variables nouvelles, sauf qu’elle ne sera plus périodique par rapport à $y_{1}.$

Les nouvelles équations canoniques admettront comme relations invariantes

$x_{1}'=x_{i}'=y_{1}'=0,$

ce qui prouve que pour $x_{1}'=x_{i}'=y_{1}'=0,$ on a

${\frac {d\mathrm {F} }{dy_{1}'}}={\frac {d\mathrm {F} }{dy_{i}'}}={\frac {d\mathrm {F} }{dx_{1}'}}=0$

et que, de plus, $\mathrm {F}$ se réduit à une constante $\mathrm {A} \,;$ je poserai alors

$\mathrm {F} '=\mathrm {F} -\mathrm {A}$

et je verrai que, si l’on développe $\mathrm {F} '$ suivant les puissances de $x_{1}',$ des $x_{i}'$ et de $y_{1}',$ il n’y aura pas de terme de degré 0 et que les seuls termes du premier degré seront des termes en $x_{2}',$ $x_{3}',$ $\ldots ,\,x_{n}'.$

Considérant alors l’équation

$\mathrm {F} '\left({\frac {d\mathrm {S} '}{dy_{i}'}},\,y_{1}'\right)=0,$

cherchons à y satisfaire en faisant

$\mathrm {S} '={\textstyle \sum }\,\mu ^{\frac {p}{2}}\mathrm {S} _{p}'$

et déterminons par récurrence les fonctions $\mathrm {S} _{p}'.$

Le calcul se poursuivra tout à fait comme au n^o 208.

Les fonctions $\mathrm {S} _{p}'$ et leurs dérivées seraient encore ici des fonctions de $y_{1}'$ et l’on verrait encore ici que ces fonctions ne deviennent pas infinies pour $y_{1}'=0\,;$ au contraire $y_{1}'=0$ est un zéro double pour les

${\frac {d\mathrm {S} _{q}'}{dy_{i}'}}\quad (i>1)$

et un zéro simple pour les ${\frac {d\mathrm {S} _{q}'}{dy_{1}'}}\cdot$

Le raisonnement se ferait par récurrence comme au n^o 208 ; les équations conservent en effet la même forme. Je n’en reproduirai pas ici les détails. Remarquons seulement que l’équation analogue à (34) s’écrit

${\textstyle \sum }\,n_{k}^{0}\,{\frac {d\mathrm {S} _{q}'}{dy_{p}'}}=\Phi ,$

où

$\Phi ={\textstyle \sum }\,\mathrm {A} \cos(m_{2}y_{2}'+\ldots +m_{n}y_{n}'+\omega )$

est une fonction périodique de $y_{2},$ $y_{3},$ $\ldots ,\,y_{n}$ dont la valeur moyenne est nulle. Les coefficients $\mathrm {A}$ et $\omega$ sont des fonctions de $y_{1}$ qui, bien entendu, ne sont pas les mêmes pour les différents termes ; on en tire

${\frac {d\mathrm {S} _{q}'}{dy_{k}'}}=\sum {\frac {\mathrm {A} \,m_{k}}{n_{2}^{0}m_{2}+\ldots +n_{n}^{0}m_{n}}}\cos(m_{2}y_{2}'+\ldots +m_{n}y_{n}'+\omega ).$

Dire que $y_{1}'=0$ est un zéro double pour $\Phi ,$ c’est dire évidemment que c’en est encore un pour chacun des coefficients $\mathrm {A}$ et par conséquent pour ${\frac {d\mathrm {S} _{q}'}{dy_{k}'}}\cdot$

Le reste du raisonnement est tout à fait pareil à celui du n^o 208.

Les fonctions $\mathrm {S} _{q}'$ sont donc finies et l’on en conclurait comme au n^o 208 qu’il en est de même des fonctions $\mathrm {S} _{q}$ et, par conséquent, que les relations (29) sont satisfaites d’elles-mêmes.

C.Q.F.D.

Relation avec les séries du n^o 125.

211.Au n^o 125 nous avons défini certaines séries $\mathrm {S}$ dont les premiers termes convergent d’une façon suffisamment rapide si aucune des combinaisons

$m_{1}n_{1}^{0}+m_{2}n_{2}^{0}+\ldots +m_{n}n_{n}^{0}$

n’est très petite. Aux n^os 204 et suivants, nous avons défini d’autres séries $\mathrm {S}$ dont la convergence reste suffisante même quand une de ces combinaisons est très petite.

Comment peut-on passer des unes aux autres ? Ce que nous avons dit au n^o 201 nous permet déjà de le prévoir.

La fonction $\mathrm {S}$ définie au n^o 125 dépend (p. 20) d’une infinité de séries de $n$ constantes arbitraires ; à savoir de

${\begin{array}{c}{\begin{array}{rrrr}x_{1}^{0},&x_{2}^{0},&\ldots ,&x_{n}^{0},\\\alpha _{1.1},&\alpha _{1.2},&\ldots ,&\alpha _{1.n},\\\alpha _{2.1},&\alpha _{2.2},&\ldots ,&\alpha _{2.n},\end{array}}\\\ldots \ldots \ldots \ldots \ldots \ldots \ldots \ldots \end{array}}$

Mais nous ne restreignons pas la généralité en supposant que tous les $\alpha _{i.k}$ sont nuls.

Soit en effet

(1)

$\mathrm {S} ^{\star }=\mathrm {S} _{0}^{\star }+\mu \,\mathrm {S} _{1}^{\star }+\mu ^{2}\,\mathrm {S} _{2}^{\star }+\ldots$

celle des fonctions $\mathrm {S}$ que l’on obtient en annulant tous les $\alpha _{i.k}\,;$ elle ne contiendra plus que $n$ constantes arbitraires

$x_{1}^{0},\quad x_{2}^{0},\quad \ldots ,\quad x_{n}^{0}.$

Les $x_{i}^{0}$ étant des constantes arbitraires, nous pouvons les remplacer par des développements quelconques procédant suivant les puissances des $\mu .$

Nous remplacerons donc $x_{i}^{0}$ par

$x_{i}^{0}=\mu \,\beta _{1.i}+\mu ^{2}\,\beta _{2.i}+\ldots ,$

les $\beta$ étant des constantes quelconques. La fonction $\mathrm {S}$ à laquelle conduit cette substitution satisfait comme $\mathrm {S} ^{\star }$ à l’équation (4) du n^o 120 ; mais les $\alpha _{i.k}$ ne sont plus nulles et il est clair que l’on peut choisir les arbitraires $\beta$ de façon que les valeurs des $\alpha$ soient tout à fait quelconques. La fonction ainsi obtenue est donc la fonction $\mathrm {S}$ la plus générale.

Revenons à $\mathrm {S} ^{\star }\,;$ cette fonction dépend des $n$ constantes $x_{i}^{0}\,;$ mais, d’autre part, les $n$ moyens mouvements $n_{i}^{0}$ sont aussi des fonctions des $x_{i}^{0},$ et inversement les $x_{i}^{0}$ sont des fonctions des $n_{i}^{0},$ de sorte que nous pourrons considérer $\mathrm {S} ^{\star }$ comme dépendant de $n$ constantes arbitraires

$n_{1}^{0},\quad n_{2}^{0},\quad \ldots ,\quad n_{n}^{0}.$

De quelle manière les fonctions $\mathrm {S} _{p}^{\star }$ dépendent-elles de ces constantes ? Chaque terme de $\mathrm {S} _{p}^{\star }$ contient en facteur le sinus ou le cosinus d’un angle de la forme

$p_{1}y_{1}+p_{2}y_{2}+\ldots +p_{n}y_{n}$(les $p$ entiers)

et le coefficient de ce sinus ou de ce cosinus est égal à une fonction holomorphe des $n_{i}^{0}$ divisée par un produit de facteurs de la forme

$q_{1}n_{1}^{0}+q_{2}n_{2}^{0}+\ldots +q_{n}n_{n}^{0}$(les $q$ entiers).

Ce sont des facteurs que l’on appelle les petits diviseurs.

En raisonnant comme nous l’avons fait au n^o 201, on verrait qu’aucun des termes de $\mathrm {S} _{p}^{\star }$ ne peut contenir plus de $2p-1$ petits diviseurs au dénominateur.

Si l’un de ces petits diviseurs, par exemple

$m_{1}n_{1}^{0}+m_{2}n_{2}^{0}+\ldots +m_{n}n_{n}^{0},$

était très petit, la convergence de la série $\mathrm {S} ^{\star }$ deviendrait illusoire ; remplaçons alors comme au n^o 202 les constantes d’intégration $n_{i}^{0}$ par divers développements procédant non plus suivant les puissances de $\mu ,$ mais suivant celles de ${\sqrt {\mu }}\,;$ soit, par exemple,

(2)

$n_{i}^{0}=\alpha _{i}^{0}+{\sqrt {\mu }}\,\alpha _{i}^{1}+\mu \,\alpha _{i}^{2}+\ldots .$

Je suppose que

$m_{1}\alpha _{1}^{0}+m_{2}\alpha _{2}^{0}+\ldots +m_{n}\alpha _{n}^{0}=0.$

Il en résultera que le développement de

$m_{1}n_{1}^{0}+m_{2}n_{2}^{0}+\ldots +m_{n}n_{n}^{0}$

commencera par un terme en ${\sqrt {\mu }}.$

Soit alors

(3)

${\begin{array}{l}\mathrm {N} \cos \\\mathrm {P} \sin \end{array}}\left(p_{1}y_{1}+p_{2}y_{2}+\ldots +p_{n}y_{n}\right)$

un terme quelconque de $\mathrm {S} _{p}^{\star },$ où $\mathrm {P}$ représente le produit des petits diviseurs.

Alors $\mathrm {N}$ et $\mathrm {P}$ seront développables suivant les puissances croissantes de ${\sqrt {\mu }}$ et l’exposant de $\mu$ dans le premier terme du développement de $\mathrm {P}$ sera au plus égal à $p-{\tfrac {1}{2}}\cdot$

Il résulte de là que $\mathrm {S} ^{\star },$ après qu’on y a substitué, à la place des $n_{i}^{0},$ leurs valeurs (2), est développable suivant les puissances positives de ${\sqrt {\mu }}.$

Soit alors

(4)

$\mathrm {S} ^{\star }=\mathrm {S} _{0}'+{\sqrt {\mu }}\,\mathrm {S} _{1}'+\mu \,\mathrm {S} _{2}'+\ldots$

ce développement ; il est clair que les divers développements (4) que l’on peut ainsi obtenir ne diffèrent pas des développements qui ont fait l’objet de ce Chapitre et que nous avons appris à former dans les n^os 204 à 207. Étudions, en particulier, les premiers termes $\mathrm {S} _{0}'$ et $\mathrm {S} _{1}'.$

On trouvera

$\mathrm {S} _{0}'=\mathrm {S} _{0}^{\star }=x_{1}^{0}y_{1}+x_{2}^{0}y_{2}+\ldots +x_{n}^{0}y_{n}.$

Les $x_{i}^{0}$ sont des constantes ; ces constantes sont elles-mêmes des fonctions connues des $n_{i}^{0}$ et dans $\mathrm {S} _{0}'$ il faut y remplacer les $n_{i}^{0}$ par les $\alpha _{i}^{0},$ puisque, pour $\mu =0,$ le développement (2) de $n_{i}^{0}$ se réduit à son premier terme, c’est-à-dire à $\alpha _{i}^{0}.$

On trouvera d’autre part

$\mathrm {S} _{1}=\xi _{1}y_{1}+\xi _{2}y_{2}+\ldots +\xi _{n}y_{n}+\mathrm {U} ,$

où

(5)

$\xi _{i}=\sum {\frac {dx_{i}^{0}}{dn_{k}^{0}}}\,\alpha _{k}^{1}.$

Les $x_{i}^{0}$ étant des fonctions connues des $n_{k}^{0},$ il en sera de même de leurs dérivées ${\frac {dx_{i}^{0}}{dn_{k}^{0}}}$ et l’on devra y remplacer les $n_{k}^{0}$ par les $\alpha _{k}^{0}.$

Quant à $\mathrm {U} ,$ il s’obtient de la manière suivante.

Prenons dans $\mathrm {S} _{p}^{\star }$ tous les termes de la forme (3) où le dénominateur $\mathrm {P}$ contiendra le petit diviseur

$m_{1}n_{1}^{0}+m_{2}n_{2}^{0}+\ldots +m_{n}n_{n}^{0}$

à la puissance $2p-1.$

Remplaçons dans le numérateur $\mathrm {N}$ les $n_{k}^{0}$ par les $\alpha _{k}^{0}$ et dans le dénominateur remplaçons

(6)

$m_{1}n_{1}^{0}+m_{2}n_{2}^{0}+\ldots +m_{n}n_{n}^{0}$

par

(7)

$m_{1}\alpha _{1}^{1}+m_{2}\alpha _{2}^{1}+\ldots +m_{n}\alpha _{n}^{1}=\gamma \,;$

ce terme deviendra

(8)

${\frac {\mathrm {N} _{0}}{\gamma ^{2p-1}}}{\begin{array}{l}\cos \\\sin \end{array}}\left(p_{1}y_{1}+p_{2}y_{2}+\ldots +p_{n}y_{n}\right),$

où $\mathrm {N} _{0}$ est ce que devient $\mathrm {N}$ quand on y remplace les $n_{i}^{0}$ par les $\alpha _{i}^{0}.$

Opérons de même pour tous les termes de $\mathrm {S} _{p}^{\star }$ qui contiennent le petit diviseur (6) à la puissance $2p-1$ et soit

${\frac {\mathrm {U} _{p}}{\gamma ^{2p-1}}}$

la somme de tous les termes de la forme (8) ainsi obtenus.

Opérons encore de même sur toutes les fonctions $\mathrm {S} _{1}^{\star },$ $\mathrm {S} _{2}^{\star },\,\ldots ,$ ce qui nous donnera successivement

${\frac {\mathrm {U} _{1}}{\gamma }},\quad {\frac {\mathrm {U} _{2}}{\gamma ^{3}}},\quad \ldots .$

On aura alors

$\mathrm {U} ={\frac {\mathrm {U} _{1}}{\gamma }}+{\frac {\mathrm {U} _{2}}{\gamma ^{3}}}+{\frac {\mathrm {U} _{3}}{\gamma ^{5}}}+\ldots .$

Si nous supposons maintenant que l’hypothèse (9) du n^o 204 soit satisfaite, nous devrons avoir

${\frac {\xi _{1}}{m_{1}}}={\frac {\xi _{2}}{m_{2}}}=\ldots ={\frac {\xi _{n}}{m_{n}}}\cdot$

En combinant ces relations avec (5) et avec (7), on peut écrire

$\xi _{i}=m_{i}\mathrm {A} \gamma ,$

$\mathrm {A}$ étant un coefficient facile à calculer, dépendant des entiers $m_{i}$ et des dérivées ${\frac {dx_{i}^{0}}{dn_{k}^{0}}}\cdot$

On en tire

(9)

${\frac {d\mathrm {S} _{1}'}{dy_{1}}}=m_{1}\mathrm {A} \gamma +{\frac {1}{\gamma }}\,{\frac {d\mathrm {U} _{1}}{dy_{1}}}+{\frac {1}{\gamma ^{3}}}\,{\frac {d\mathrm {U} _{2}}{dy_{1}}}+\ldots ,$

et l’on en conclut que le carré du second membre de l’équation (9), qui doit comme ce second membre lui-même procéder suivant les puissances décroissantes de $\gamma ,$ se réduira à ses deux premiers termes

$m_{1}^{2}\mathrm {A} ^{2}\gamma ^{2}+2m_{1}\mathrm {A} {\frac {d\mathrm {U} _{1}}{dy_{1}}}\cdot$

Il en résulte une série d’identités

${\begin{aligned}2m_{1}\mathrm {A} {\frac {d\mathrm {U} _{2}}{dy_{1}}}+\left({\frac {d\mathrm {U} _{1}}{dy_{1}}}\right)^{2}&=0,\\2m_{1}\mathrm {A} {\frac {d\mathrm {U} _{3}}{dy_{1}}}+2{\frac {d\mathrm {U} _{1}}{dy_{1}}}{\frac {d\mathrm {U} _{2}}{dy_{2}}}&=0,\\\ldots \ldots \ldots \ldots \ldots \ldots \ldots \ldots &\ldots .,\end{aligned}}$

qui, indépendamment même des applications en vue desquelles ce Chapitre est écrit, sont des propriétés curieuses et inattendues du développement (1).

Divergence des séries.

212.Les séries que nous avons obtenues dans ce Chapitre sont divergentes au même titre que celles de MM. Newcomb et Lindstedt.

Considérons en effet une des séries $\mathrm {S}$ définies au n^o 204. Cette série dépendra d’un certain nombre de constantes arbitraires.

Nous avons en premier lieu

$x_{1}^{0},\quad x_{2}^{0},\quad \ldots ,\quad x_{n}^{0}.$

Ces constantes sont liées entre elles par la relation

$m_{1}n_{1}^{0}+m_{2}n_{2}^{0}+\ldots +m_{n}n_{n}^{0}=0.$

Supposons, comme dans les n^os 205 et suivants,

$m_{1}=1,\quad m_{2}=m_{3}=\ldots =m_{n}=0\,;$

nous avons vu que cela était toujours permis ; notre relation deviendra

$-n_{1}^{0}={\frac {d\mathrm {F} _{0}}{dx_{1}^{0}}}=0.$

Cette équation pourra être résolue par rapport à $x_{1}^{0},$ ce qui donnera

(1)

$x_{1}^{0}=\varphi (x_{2}^{0},\,x_{3}^{0},\,\ldots ,\,x_{n}^{0}),$

de plus ces $n$ constantes sont liées à $\mathrm {C} _{0}$ par la relation

$\mathrm {F} _{0}(x_{1}^{0},\,x_{2}^{0},\,x_{3}^{0},\,\ldots ,\,x_{n}^{0})=\mathrm {C} _{0}.$

Nous avons ensuite, outre $\mathrm {C} _{0},$

$\mathrm {C} _{2},\quad \mathrm {C} _{4},\quad \mathrm {C} _{6},\quad \ldots .$

Nous avons enfin

${\begin{array}{c}\alpha _{1},\quad \alpha _{2},\quad \ldots ,\quad \alpha _{n},\\\ldots \ldots \ldots \ldots \ldots \ldots \ldots ,\\\alpha _{1}^{p},\quad \alpha _{2}^{p},\quad \ldots ,\quad \alpha _{n}^{p},\\\ldots \ldots \ldots \ldots \ldots \ldots \ldots .\end{array}}$

Mais nous pouvons, sans restreindre la généralité, supposer que ces quantités sont liées entre elles par les relations (9) et (10) du n^o 204, ou mieux encore nous pouvons, sans restreindre la généralité, supposer que toutes ces quantités $\alpha _{i}$ et $\alpha _{i}^{p}$ sont nulles.

Les constantes $\mathrm {C} _{4},$ $\mathrm {C} _{6},\,\ldots$ sont liées par certaines relations aux arbitraires $\alpha _{i}$ et $\alpha _{i}^{p}.$ Si l’on suppose donc que les $\alpha _{i}$ et les $\alpha _{i}^{p}$ sont nulles, $\mathrm {C} _{4},$ $\mathrm {C} _{6},\,\ldots$ deviennent des fonctions entièrement déterminées des $x_{i}^{0}$ et de $\mathrm {C} _{2}.$

Il nous reste donc en tout $n$ arbitraires

$x_{2}^{0},\quad x_{3}^{0},\quad \ldots ,\quad x_{n}^{0},$et$\mathrm {C} _{2},$

puisque $x_{1}^{0}$ est lié aux autres $x_{i}^{0}$ par une relation.

Considérons maintenant les relations

(2)

${\begin{aligned}x_{1}&={\frac {d\mathrm {S} }{dy_{1}}},&x_{2}&={\frac {d\mathrm {S} }{dy_{2}}},&&\ldots ,&x_{n}&={\frac {d\mathrm {S} }{dy_{n}}}\cdot \end{aligned}}$

Les seconds membres sont des fonctions de

$y_{1},\quad y_{2},\quad \ldots ,\quad y_{n},\quad x_{2}^{0},\quad x_{3}^{0},\quad \ldots ,\quad x_{n}^{0},\quad \mathrm {C} _{2}.$

Résolvons alors les équations (2) par rapport à

$x_{2}^{0},\quad x_{3}^{0},\quad \ldots ,\quad x_{n}^{0},\quad \mathrm {C} _{2},$

il viendra

(3)

$\left\{{\begin{aligned}x_{i}^{0}&=\psi _{i}(x_{1},x_{2},\ldots ,x_{n},y_{1},y_{2},\ldots ,y_{n})\quad (i=2,\,3,\,\ldots n),\\\mathrm {C} _{2}&=\theta (x_{1},x_{2},\ldots ,x_{n},y_{1},y_{2},\ldots ,y_{n}).\end{aligned}}\right.$

Si les séries $\mathrm {S}$ étaient convergentes, les $\psi _{i}$ et $\theta$ seraient des intégrales des équations différentielles.

Voyons quelle en serait la forme.

Plaçons-nous d’abord dans le cas du n^o 204 et supposons par conséquent que $\mathrm {C} _{2}$ soit plus grand que le maximum de ${\big [}\mathrm {F} _{1}{\big ]}\,;$ Il en résulte que

${\sqrt {\mathrm {C} _{2}-{\big [}\mathrm {F} _{1}{\big ]}}},\quad {\frac {1}{\sqrt {\mathrm {C} _{2}-{\big [}\mathrm {F} _{1}{\big ]}}}},$

seront des fonctions holomorphes de $\mathrm {C} _{2},$ $y_{1},$ $y_{2},$ $\ldots ,\,y_{n},$ pour toutes les valeurs réelles des $y_{i}$ et pour les valeurs de $\mathrm {C} _{2}$ voisines de celle que l’on considère.

Nous avons supposé dans ce qui précède que $\mathrm {F}$ est une fonction holomorphe des $x_{i}$ et des $y_{i}$ pour toutes les valeurs réelles des $y_{i}$ et pour les valeurs des $x_{i}$ voisines des $x_{i}^{0}.$

De plus, la dérivée seconde de $\mathrm {F} _{0}$ par rapport à $x_{1}^{0}$ ne sera pas nulle en général, de sorte que $x_{1}^{0}$ sera une fonction holomorphe des autres $x_{i}^{0}.$

Il résulte de tout cela que les ${\frac {d\mathrm {S} _{p}}{dy_{i}}}$ seront des fonctions holomorphes pour toutes les valeurs réelles des $y_{i}$ et pour les valeurs de

$x_{2}^{0},\quad x_{3}^{0},\quad \ldots ,\quad x_{n}^{0},\quad \mathrm {C} _{2}.$

voisines de celles que l’on considère.

Soient donc

$\lambda _{1},\quad \lambda _{2},\quad \ldots ,\quad \lambda _{n},\quad \gamma$

des valeurs de ces constantes voisines de celles que l’on considère. Posons

$\lambda _{1}=\varphi (\lambda _{2},\lambda _{3},\ldots ,\lambda _{n}).$

Les deux membres des équations (2) vont être développables suivant les puissances de

${\begin{array}{rrrrrr}{\sqrt {\mu }},&x_{1}-\lambda _{1},&x_{2}-\lambda _{2},&\ldots ,&x_{n}-\lambda _{n},\\&x_{1}^{0}-\lambda _{1},&x_{2}^{0}-\lambda _{2},&\ldots ,&x_{n}^{0}-\lambda _{n},&\mathrm {C} _{2}-\gamma ,\end{array}}$

et suivant les sinus et cosinus des multiples des $y_{i}.$

Mais, avant d’appliquer le théorème du n^o 30 aux équations (2), nous allons transformer l’une de ces équations. À cet effet, posons

$x_{1}=\varphi (x_{2},x_{3},\ldots ,x_{n})+{\sqrt {\mu }}\,x_{1}'.$

Alors la première équation (2) devient

$\varphi (x_{2},x_{3},\ldots ,x_{n})+{\sqrt {\mu }}\,x_{1}'=\varphi (x_{0},x_{3}^{0},\ldots ,x_{n}^{0})+{\sqrt {\mu }}\,{\frac {d\mathrm {S} _{1}}{dy_{1}}}+\mu \,{\frac {d\mathrm {S} _{2}}{dy_{1}}}+\ldots ,$

ou, en tenant compte des autres équations (2),

${\begin{aligned}{\sqrt {\mu }}\,x_{1}'=&\varphi \left({\frac {d\mathrm {S} }{dy_{2}}},{\frac {d\mathrm {S} }{dy_{3}}},\ldots ,{\frac {d\mathrm {S} }{dy_{n}}}\right)-\varphi \left(x_{2}^{0},x_{3}^{0},\ldots ,x_{n}^{0}\right)\\&+{\sqrt {\mu }}\,{\frac {d\mathrm {S} _{1}}{dy_{1}}}+\mu \,{\frac {d\mathrm {S} _{2}}{dy_{1}}}+\ldots ,\end{aligned}}$

Or nous savons que ${\frac {d\mathrm {S} _{1}}{dy_{2}}},$ ${\frac {d\mathrm {S} _{1}}{dy_{3}}},$ $\ldots ,\,{\frac {d\mathrm {S} _{1}}{dy_{n}}}$ sont nuls, ce qui veut dire que les différences

${\frac {d\mathrm {S} }{dy_{i}}}-x_{i}^{0}\quad (i>1),$

et par conséquent la différence

$\varphi \left({\frac {d\mathrm {S} }{dy_{i}}}\right)-\varphi (x_{i}^{0}),$

sont divisibles par $\mu .$ Je puis donc poser

$\varphi \left({\frac {d\mathrm {S} }{dy_{2}}},{\frac {d\mathrm {S} }{dy_{3}}},\ldots ,{\frac {d\mathrm {S} }{dy_{n}}}\right)-\varphi \left(x_{2}^{0},x_{3}^{0},\ldots ,x_{n}^{0}\right)=\mu \,\mathrm {H} ,$

d’où

(4)

$x_{1}'={\frac {d\mathrm {S} _{1}}{dy_{1}}}+\mathrm {H} \,{\sqrt {\mu }}+{\frac {d\mathrm {S} _{2}}{dy_{1}}}\,{\sqrt {\mu }}+{\frac {d\mathrm {S} _{3}}{dy_{1}}}\,\mu +\ldots .$

Adjoignons à cette équation (4) les $n-1$ dernières équations (2). Nous aurons ainsi un système de $n$ équations dont les deux membres seront développables suivant les puissances de

${\begin{array}{rrrrrr}{\sqrt {\mu }},&x_{1}',&x_{2}-\lambda _{2},&\ldots ,&x_{n}-\lambda _{n},\\&&x_{2}^{0}-\lambda _{2},&\ldots ,&x_{n}^{0}-\lambda _{n},&\mathrm {C} _{2}-\gamma \end{array}}$

et suivant les sinus et cosinus des multiples des $y_{i}.$

Pour $\mu =0,$ ce système se réduit à

${\begin{aligned}x_{1}'&={\frac {d\mathrm {S} _{1}}{dy_{1}}},&x_{i}&=x_{i}^{0}.\end{aligned}}$

Il faut donc démontrer que, pour

${\begin{aligned}x_{1}'&=0,&x_{i}&=x_{i}^{0}=\lambda _{i},\end{aligned}}$

le déterminant fonctionnel des $x_{i}^{0}-x_{i}$ et de ${\frac {d\mathrm {S} _{1}}{dy_{1}}}-x_{1}'$ par rapport aux $x_{i}^{0}$ et à $\mathrm {C} _{2}$ ne s’annule pas. Or ce déterminant se réduit à la dérivée de ${\frac {d\mathrm {S} _{1}}{dy_{1}}}$ par rapport à $\mathrm {C} _{2}$ ou, si

${\frac {d\mathrm {S} _{1}}{dy_{1}}}=\mathrm {A} \,{\sqrt {\mathrm {C} _{2}-{\big [}\mathrm {F} _{1}{\big ]}}},$

à

${\frac {\mathrm {A} }{2{\sqrt {\mathrm {C} _{2}-{\big [}\mathrm {F} _{1}{\big ]}}}}}\cdot$

Il n’est donc pas nul et le théorème du n^o 30 est applicable ; si donc nos séries étaient convergentes, nos équations différentielles admettraient $n$ intégrales $\psi _{i}$ et $\theta$ uniformes par rapport aux $x$ et aux $y,$ et périodiques par rapport aux $y.$ Or cela est impossible. Donc les séries divergent.

C.Q.F.D.

Le même résultat subsiste dans le cas de la libration ; pour s’en convaincre, on n’a qu’à se rappeler qu’au n^o 206 nous avons ramené nos équations, par un changement de variables convenable, à la forme des équations du n^o 134. En raisonnant comme au Chapitre XIII, on montrerait donc encore que la convergence des séries entraînerait l’existence d’intégrales uniformes, contrairement au théorème du Chapitre V.

Même dans le cas limite, les séries sont encore divergentes, mais je ne pourrai le démontrer rigoureusement que plus loin.

On peut se demander par quel mécanisme, pour ainsi dire, les termes de ces séries sont susceptibles de croître de façon à empêcher la convergence.

Dans le cas particulier où il n’y a que deux degrés de liberté, il ne s’introduit pas de petits diviseurs.

En effet, les équations que l’on a à intégrer sont alors de l’une des deux formes

${\begin{aligned}n_{2}^{0}\,{\frac {d\mathrm {S} _{p}}{dy_{2}}}&=\Phi ,\\{\frac {d\mathrm {S} _{1}}{dy_{1}}}{\frac {d[\mathrm {S} _{p}]}{dy_{1}}}&=\Phi \end{aligned}}$

et les seuls diviseurs qui s’introduisent, $n_{2}^{0}m_{2}$ et ${\frac {d\mathrm {S} _{1}}{dy_{1}}},$ ne sont pas très petits.

En revanche on a à effectuer des différentiations et, en différentiant un terme contenant le cosinus ou le sinus de

$p_{1}y_{1}+p_{2}y_{2}+\ldots p_{n}y_{n},$

on introduit en multiplicateur un des entiers $p_{i}$ qui peut être très grand.

Ce qui empêche la convergence, ce n’est donc pas la présence de petits diviseurs s’introduisant par l’intégration, mais celle de grands multiplicateurs s’introduisant par la différentiation.

On peut aussi présenter la chose d’une autre manière.

On a, dans le cas du n^o 125 et s’il n’y a que deux degrés de liberté, de petits diviseurs de la forme

$m_{1}n_{1}^{0}+m_{2}n_{2}^{0}\,;$

remplaçons-y $n_{1}^{0}$ et $n_{2}^{0}$ par des développements analogues aux développements (2) du numéro précédent. Soit, par exemple,

${\begin{aligned}n_{2}^{0}&=\alpha _{2},&n_{1}^{0}&=\alpha _{1}{\sqrt {\mu }}.\end{aligned}}$

Nos petits diviseurs deviendront

$m_{2}\alpha _{2}+m_{1}\alpha _{1}{\sqrt {\mu }}.$

L’expression

${\frac {1}{m_{2}\alpha _{2}+m_{1}\alpha _{1}{\sqrt {\mu }}}}$

peut se développer suivant les puissances de ${\sqrt {\mu }}$ et l’on trouve

(5)

${\frac {1}{m_{2}\alpha _{2}}}+{\sqrt {\mu }}\,{\frac {m_{1}\alpha _{1}}{(m_{2}\alpha _{2})^{2}}}+\mu \,{\frac {(m_{1}\alpha _{1})^{2}}{(m_{2}\alpha _{2})^{3}}}+\ldots .$

Aucun des termes de ce développement ne contient au dénominateur un très petit diviseur ; car $m_{2}\alpha _{2}$ n’est jamais très petit.

Il est clair pourtant que, quelque petit que soit $\mu ,$ on pourra trouver des nombres entiers $m_{1}$ et $m_{2}$ tels que

${\sqrt {\mu }}\,{\frac {m_{1}\alpha _{1}}{m_{2}\alpha _{2}}}>1$

et tels par conséquent que le développement (5) diverge. On s’explique donc comment, en substituant, comme je l’ai fait au numéro précédent, à la place des moyens mouvements leurs développements (2) et ordonnant ensuite suivant les puissances de ${\sqrt {\mu }},$ on arrive à des séries divergentes.

On rapprochera ce que je viens de dire de ce que j’ai dit aux n^os 109 et suivants.